Künstliche Neuronale Netzwerke (KNN) sind das am häufigsten verwendete Buzzword im Zusammenhang mit Künstlicher Intelligenz und Machine Learning. In diesem Beitrag wollen wir uns den Aufbau von einfachen Netzwerken genauer anschauen und hoffentlich vielen die Angst davor nehmen.
Wir werden versuchen in dieser Einführung mit so wenig Mathematik wie möglich auszukommen, sodass auch Leser, die mit dem Thema Machine Learning noch nicht vertraut sind einen einfachen Zugang zu dem Thema bekommen.
Künstliche Neuronale Netzwerke orientieren sich am biologischen Aufbau des menschlichen Gehirns. Damit werden computerbasiert schwierige Problemstellungen und mathematische Berechnungen modelliert und gelöst.
Was sind die Neuronen?
In unserem Gehirn werden die aufgenommenen Informationen der Sinnesorgane in sogenannten Neuronen aufgenommen. Diese verarbeiten die Information und geben anschließend einen Output weiter, der zu einer Reaktion des Körpers führt. Die Informationsverarbeitung findet dabei nicht nur in einem einzelnen Neuron statt, sondern in einem vielschichtigen Netzwerk von Knoten.
Im Künstlichen Neuronalen Netzwerk wird dieses biologische Prinzip nachgestellt und mathematisch ausgedrückt. Das Neuron (auch Knoten oder Unit genannt) verarbeitet einen oder mehrere Inputs und errechnet daraus einen einzigen Output. Dabei werden drei Schritte ausgeführt:
- Die verschiedenen Inputs x werden mit einem Gewichtsfaktor w multipliziert:
\(\) \[x_1 \rightarrow x_1 \cdot w_1, x_2 \rightarrow x_2 \cdot w_2 \]
Die Gewichtsfaktoren entscheiden darüber, wie wichtig ein Input für das Neuron ist, um die Problemstellung lösen zu können. Wenn ein Input sehr wichtig, wird der Wert für den Faktor w größer. Ein unwichtiger Input hat einen Wert von 0.
- Alle gewichteten Inputs des Neurons werden aufsummiert. Zusätzlich wird noch ein Bias b hinzugefügt:
\(\) \[(x_1 \cdot w_1) + (x_2 \cdot w_2) + b \]
- Anschließend wird das Ergebnis in eine sogenannte Aktivierungsfunktion gegeben.
\(\) \[y = f(x_1 \cdot w_1) + (x_2 \cdot w_2) + b) \]
Es gibt verschiedene Aktivierungsfunktionen, die genutzt werden können. In vielen Fällen handelt es sich um die Sigmoid Funktion. Diese nimmt Werte und bildet sie im Bereich zwischen 0 und 1 ab:
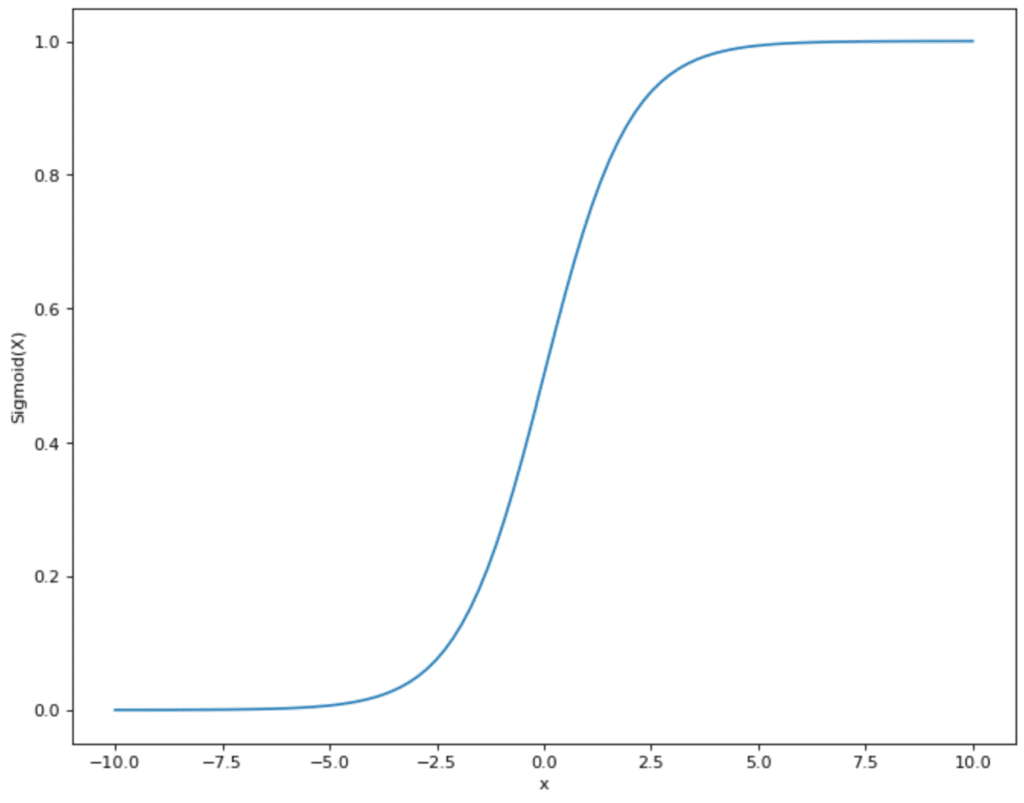
Das hat den Vorteil für das Neuronale Netzwerk, dass alle Werte die aus Schritt 2 kommen, sich in einem vorgegebenen kleineren Rahmen bewegen. Die Sigmoid Funktion schränkt also Werte, die theoretisch zwischen (- ∞, + ∞) liegen können und bildet sie im Bereich zwischen (0,1) ab.
Nachdem wir nun verstanden haben, was ein einzelnes Neuron für Funktionen hat und was die einzelnen Schritte innerhalb des Knotens sind, können wir uns nun dem Künstlichen Neuronalen Netzwerk zuwenden. Dies ist lediglich eine Sammlung dieser Neuronen, die in verschiedenen Schichten organisiert sind.
Welche Schichten enthält ein Künstliches Neuronales Netzwerk?
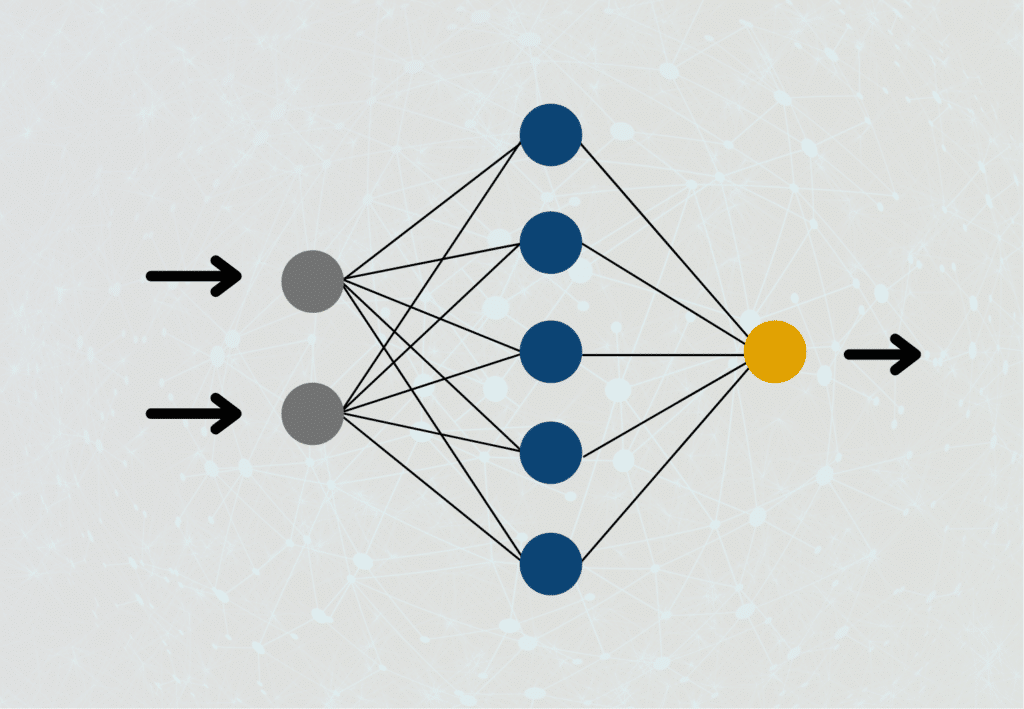
Die Informationen durchlaufen das Netzwerk in verschiedenen Schichten:
- Eingabeschicht: Hier werden die Inputs für das Modell eingegeben und in den Neuronen verarbeitet, bevor sie weitergereicht werden an die nächste Schicht.
- Verborgene Schicht(en): Eine oder mehrere sogenannte Hidden Layer übernehmen die eigentliche Informationsverarbeitung. Die Eingaben aus vorherigen Schichten werden gewichtet in einem Neuron verarbeitet und an die nachfolgende Schicht weitergegeben. Dies geschieht solange bis die Ausgabeschicht erreicht ist. Da die Berechnungen in dieser Schicht nicht sichtbar sind, sondern im “verborgenenen” stattfinden, werden diese Ansammlungen an Neuronen als Hidden Layers oder verborgenenen Schichten bezeichnet.
- Ausgabeschicht: Diese Schicht schließt an die letzte verborgene Schicht und übernimmt die Outputs der Neuronen. Die Ergebnisse der Knoten in diesem Layer beinhalten das schlussendliche Ergebnis bzw. die Entscheidung des Neuronalen Netzwerks dar.
Wie lernen Künstliche Neuronale Netzwerke?
Im Zusammenhang mit KI wird oft davon geredet, dass die Modelle trainiert werden müssen und viele Daten benötigt werden, um gute Ergebnisse liefern zu können. Doch was bedeutet dieser Prozess genau für das Künstliche Neuronale Netzwerk?
Aus den Daten wird für jeden einzelnen Datensatz das Ergebnis berechnet, das beim Durchlaufen des Netzwerks entsteht und verglichen, wie gut das Ergebnis des Netzwerkes ist im Vergleich zu dem tatsächlichen Ergebnis aus dem Datensatz. Dabei soll die Vorhersage des Künstlichen Neuronalen Netzwerkes immer genauer an das tatsächliche Ergebnis herankommen.
Das Neuronale Netzwerk hat dazu eine Stellschraube, um das Ergebnis mit jedem Trainingsschritt an den tatsächlichen Outcome heranbringen zu können, nämlich die Gewichtung der Outputs der einzelnen Neuronen. Im Lernprozess werden deren Gewichtungen ständig verändert, um die Genauigkeit des Ergebnisses zu verändern. Das heißt jedes Neuron entscheidet, welche Outputs der vorhergegangen Neuronen für ihre Berechnung wichtig sind und welche nicht. Im besten Fall festigt sich dieses Gewicht mit jedem neuen Datensatz und das gesamte Ergebnis wird genauer.
Hierzu ein kleines Beispiel zur Verdeutlichung, welches selbstverständlich nicht zur Nachahmung empfohlen wird. Im Mathe Unterricht sitzen insgesamt drei gute FreundInnen neben dir. Bei jeder Aufgabe, die im Unterricht gerechnet wird, kannst du alle drei fragen, ob sie dir ihr Ergebnis nennen, weil du selbst nicht weiterkommst. Alle drei nennen dir auch immer bereitwillig eine Zahl als Lösung. Deshalb möchtest du während den Unterrichtsstunden (der Trainingsphase) herausfinden, welcher der drei Mitschüler meistens das beste Ergebnis hat.
Bei jeder Aufgabe, die ihr rechnet, fragst du also alle drei nach ihrem Ergebnis und entscheidest dich für eins, um es dann mit dem Ergebnis der LehrerIn zu vergleichen und herauszufinden, von welchem der drei MitschülerInnen du das beste Ergebnis erwarten kannst. Je nach Teilgebiet erkennst du, dass ein Input besser ist als ein anderer. Somit änderst du die Gewichtungen in der Trainingsphase ab und verfeinerst sie. In der Klausur weißt Du dann im Optimalfall genau, an welchen der drei Du dich wenden musst, um möglichst das korrekte Ergebnis genannt zu bekommen.
Genau das machen auch alle Neuronen im Netzwerk. Sie bekommen während dem Training eine gewisse Anzahl von Inputs genannt, abhängig davon, wie viele Neuronen in unmittelbarer Nähe “sitzen”. Im Training entscheiden sie sich in jedem Schritt, welches Vorergebnis für sie am Besten geeignet ist und vergleichen dann mit dem tatsächlichen Ergebnis, um festzustellen, ob sie richtig lagen. Nach dem Training, also in der Klausur, wissen sie dann genau, welche vorherigen Neuronen die wichtigsten sind.
Was ist die Verlustfunktion?
Das Ziel des Neuronalen Netzwerks ist es, die Differenz zwischen dem selbst vorhergesagten Ergebnis und dem tatsächlichen Ergebnis in der Realität mit jedem Trainingsschritt zu verkleinern. Um dieses Ziel erreichen zu können und den Weg dorthin tracken zu können, gibt es die sogenannte Verlustfunktion. Sie gibt eine mathematische Aussage darüber, wie weit die Antwort des Netzwerks von der gewünschten, tatsächlichen Antwort entfernt ist.
Im Optimalfall hat die Verlustfunktionen einen Wert von 0, denn dann stimmt das Ergebnis des Netzwerks genau mit dem tatsächlichen Ergebnis überein. Somit wird in jedem Trainingsschritt versucht die Verlustfunktion dem Wert 0 anzunähern. Um das Minimum der Verlustfunktion finden zu können und schnell näher zu kommen, wird beispielsweise das Gradientenverfahren genutzt.
In welchen Anwendungen werden Künstliche Neuronale Netzwerke genutzt?
Die Neuronalen Netzwerke basieren auf den Perceptrons und werden vor allem im Bereich des Machine Learnings genutzt. Das Ziel dabei ist vor allem das Erlernen von Strukturen in vorherigen Daten und die anschließende Vorhersage von neuen Werten. Einige Beispiele dafür sind:
- Objekterkennung in Bildern: Künstliche Neuronale Netzwerke können Objekte in Bildern erkennen oder Bilder einer Klasse zu zuzuordnen. Unternehmen nutzen diese Eigenschaft beispielsweise beim Autonomen Fahren, um Objekte zu erkennen, auf die das Auto reagieren sollte. Ein anderes Einsatzgebiet gibt es in der Medizin, wenn Röntgenbilder untersucht werden sollen, um beispielsweise ein frühes Stadium von Krebs zu erkennen.
- Vorhersage: Wenn Unternehmen in der Lage sind zukünftige Szenarien oder Zustände sehr genau vorhersagen zu können, können sie verschiedene Entscheidungsmöglichkeiten gut gegeneinander abwägen und die beste Option wählen. Eine qualitativ hochwertige Regressionsanalyse für den zu erwartenden Umsatz im nächsten Jahr kann beispielsweise genutzt werden, um zu entscheiden, wie viel Budget für das Marketing eingeplant werden soll.
- Kundenstimmungsanalyse: Durch das Internet haben Kunden viele Kanäle, um ihre Bewertungen der Marke oder eines Produktes öffentlich zu machen. Unternehmen müssen deshalb den Überblick darüber behalten, ob die Kunden größtenteils zufrieden sind oder nicht. Mit wenigen Rezensionen, welche als gut oder schlecht klassifiziert sind, können effiziente Modelle trainiert werden, die dann automatische eine Vielzahl von Kommentaren einordnen können.
- Spamerkennung: In vielen Mailprogrammen gibt es die Möglichkeit konkrete E-Mails als Spam zu kennzeichnen. Diese Daten werden genutzt um Machine Learning Modelle zu trainieren, die zukünftige Mails direkt als Spam kennzeichnen, sodass sie der Endnutzer gar nicht erst angezeigt bekommt.
- Analyse von Aktienkursen: Neuronale Netzwerke können auch genutzt werden, um anhand von früheren Aktienkursen die Entwicklung einer Aktie vorhersagen zu können. Dabei spielen verschiedene Einflussgrößen eine Rolle, wie beispielsweise die gesamtwirtschaftliche Lage oder neue Informationen über das Unternehmen.
Das solltest Du mitnehmen
- Künstliche Neuronale Netzwerke bestehen aus einer Vielzahl von Neuronen. Das Gewicht der einzelnen Neuronen wird während der Trainingsphase geändert und verfeinert.
- Das Netzwerk ist aus drei verschiedenen Schichttypen aufgebaut: Eingabeschicht, verborgene Schicht und Ausgabeschicht.
- Das Ziel des Künstlichen Neuronalen Netzwerkes ist es die Verlustfunktion, also die Differenz aus vorhergesagtem Ergebnis und dem tatsächlichen Ergebnis zu minimieren.
Was ist der Conjugate Gradient?
Erforschen Sie den Conjugate Gradient: Algorithmusbeschreibung, Varianten, Anwendungen und Grenzen.
Was ist ein Elastic Net?
Entdecken Sie Elastic Net: Die vielseitige Regularisierungstechnik beim Machine Learning für bessere Modellbalance und Vorhersagen.
Was ist Adversarial Training?
Sicheres maschinelles Lernen: Erklärung von Adversarial Training, dessen Anwendungen und Probleme.
Was sind Echo State Networks?
Verstehen Sie Echo State Networks: Dynamic Time-Series Modeling, Applikationen und wie man sie in Python implementiert.
Was sind Faktorgraphen?
Entdecken Sie die Vielseitigkeit von Faktorgraphen bei der grafischen Modellierung und bei praktischen Anwendungen.
Was ist Unsupervised Domain Adaptation?
Beherrschen Sie die Unsupervised Domain Adaptation: Überbrücken Sie die Lücke zwischen Quell- und Zieldomänen für Lernmodelle.
Andere Beiträge zum Thema Künstliche Neuronale Netzwerke
- Hier kannst Du das Training eines Neuronalen Netzwerkes Schritt für Schritt nachvollziehen mit echten Werten.

Niklas Lang
Seit 2020 bin ich als Machine Learning Engineer und Softwareentwickler tätig und beschäftige mich leidenschaftlich mit der Welt der Daten, Algorithmen und Softwareentwicklung. Neben meiner Arbeit in der Praxis unterrichte ich an mehreren deutschen Hochschulen, darunter die IU International University of Applied Sciences und die Duale Hochschule Baden-Württemberg, in den Bereichen Data Science, Mathematik und Business Analytics.
Mein Ziel ist es, komplexe Themen wie Statistik und maschinelles Lernen so aufzubereiten, dass sie nicht nur verständlich, sondern auch spannend und greifbar werden. Dabei kombiniere ich praktische Erfahrungen aus der Industrie mit fundierten theoretischen Grundlagen, um meine Studierenden bestmöglich auf die Herausforderungen der Datenwelt vorzubereiten.





