Artificial Neural Networks (ANN) are the most commonly used buzzword in the context of Artificial Intelligence and Machine Learning. In this article we want to take a closer look at the construction of simple networks and hopefully take away the fear of many.
We will try to use as little mathematics as possible in this introduction, so that even readers who are not yet familiar with the topic of machine learning will have an easy access to the subject.
Artificial neural networks are based on the biological structure of the human brain. This is used to model and solve difficult computer-based problems and mathematical calculations.
Building blocks: Neurons
In our brain, the information received from the sensory organs is recorded in so-called neurons. These process the information and then pass on an output that leads to a reaction of the body. Information processing takes place not only in a single neuron but in a multilayered network of nodes.
In the artificial neural network, this biological principle is replicated and expressed mathematically. The neuron (also called node or unit) processes one or more inputs and computes a single output from them. Three steps are executed in the process:
- The various inputs x are multiplied by a weight factor w:
\(\) \[x_1 \rightarrow x_1 \cdot w_1, x_2 \rightarrow x_2 \cdot w_2 \]
The weight factors decide how important input is for the neuron to be able to solve the problem. If an input is very important, the value for the factor w becomes larger. An unimportant input has a value of 0.
2. All weighted inputs of the neuron are summed. In addition, a bias b is added:
\(\) \[(x_1 \cdot w_1) + (x_2 \cdot w_2) + b \]
3. Subsequently, the result is given into a so-called activation function.
\(\) \[y = f(x_1 \cdot w_1) + (x_2 \cdot w_2) + b) \]
There are various activation functions that can be used. In many cases, it is the sigmoid function. This takes values and maps them in the range between 0 and 1:
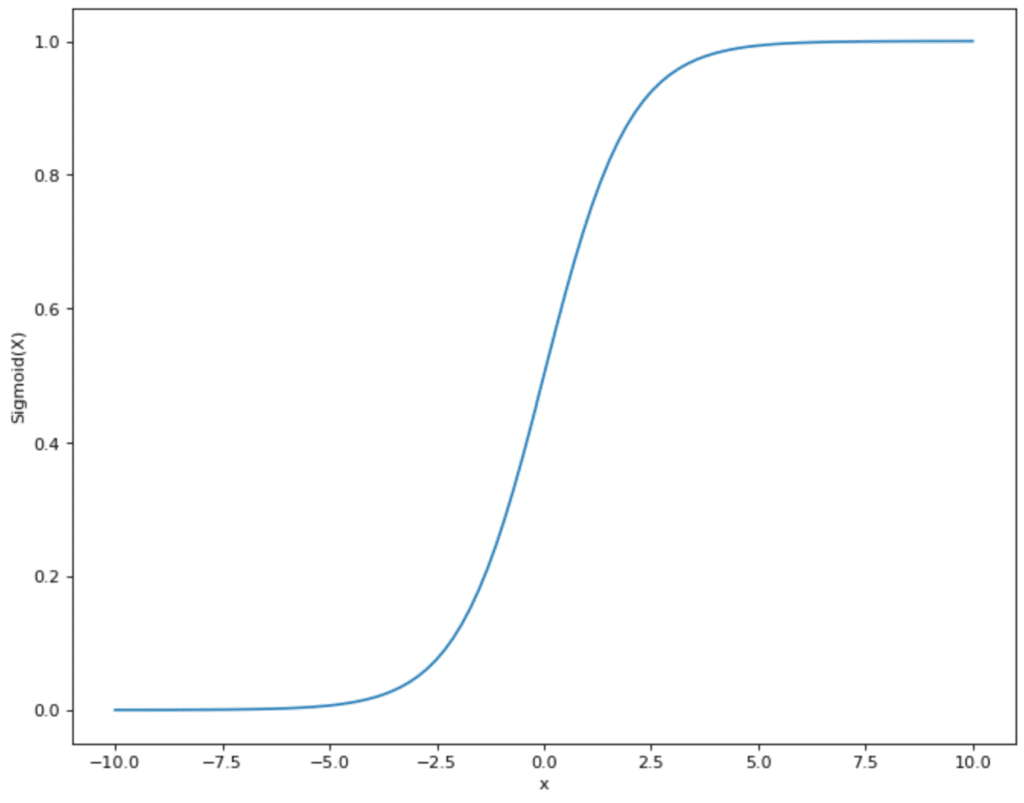
This has the advantage for the neural network that all values coming from step 2 are in a given smaller range. The sigmoid function thus restricts values that can theoretically lie between (- ∞, + ∞) and maps them in the range between (0,1).
Now that we understand what a single neuron’s functions are and what the individual steps are within the node, we can turn to the artificial neural network. This is just a collection of these neurons organized in different layers.
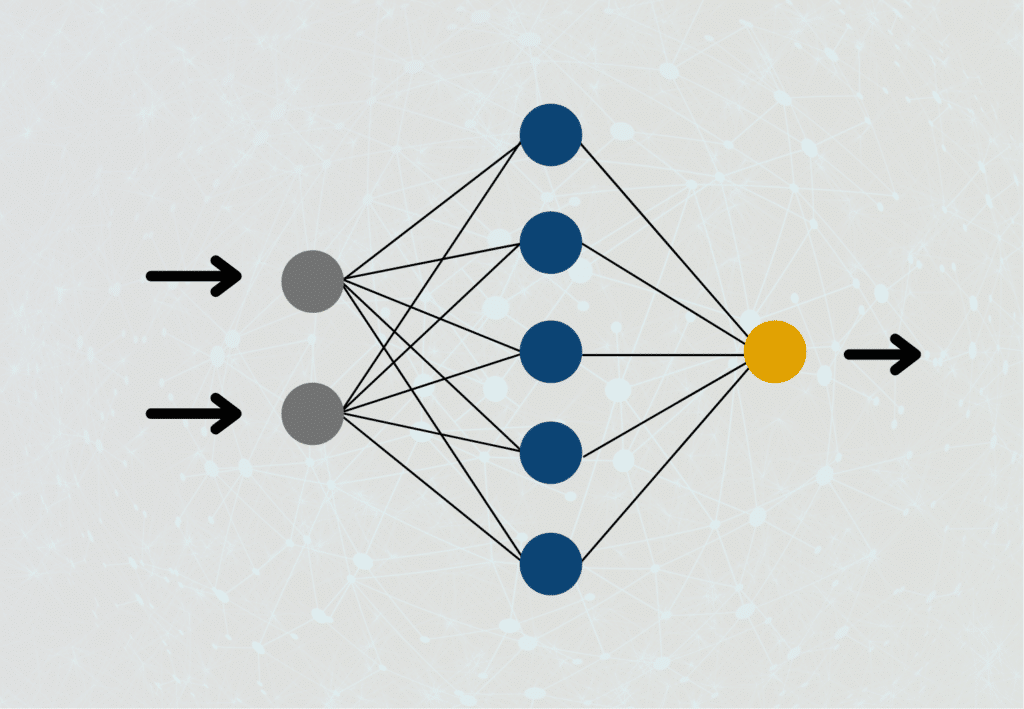
Network: input layer, hidden layer, and output layer
The information passes through the network in different layers:
- Input layer: Here the inputs for the model are entered and processed in the neurons before being passed on to the next layer.
- Hidden layer(s): One or more so-called hidden layers take over the actual information processing. The inputs from previous layers are processed in a weighted manner in a neuron and passed on to the subsequent layer. This continues until the output layer is reached. Since the calculations in this layer are not visible, but take place in the “hidden”, these collections of neurons are called hidden layers.
- Output layer: This layer follows the last hidden layer and takes the outputs of the neurons. The outputs of the nodes in this layer contain the final result or decision of the neural network.
How do Artificial Neural Networks learn?
In the context of AI, people often talk about the fact that the models have to be trained and that a lot of data is needed to be able to deliver good results. But what exactly does this process mean for artificial neural networks?
From the data, the result that is produced when the network is traversed is calculated for each individual data set and compared to see how good the result of the network is compared to the actual result from the data set. In this process, the prediction of artificial neural networks should get closer and closer to the actual result.
For this purpose, artificial neural networks have an adjusting screw to bring the result closer to the actual outcome with each training step, namely the weighting of the outputs of the individual neurons. In the learning process, their weights are constantly changed to alter the accuracy of the outcome. That is, each neuron decides which outputs of the previous neurons are important for their computation and which are not. In the best case, this weight strengthens with each new data set and the overall result becomes more accurate.
Here is a small example to illustrate this, which is of course not recommended for imitation. In math class, there are three good friends sitting next to you. For every problem that is calculated in class, you can ask all three of them to tell you their result because you can’t get any further yourself. All three of them are always willing to give you a number as a solution. Therefore, during the lessons (the training phase) you want to find out which of the three classmates usually has the best result.
So for each task you calculate, you ask all three of them for their result by comparing them with the teacher’s results and find out from which of the three classmates you can expect the best result. Depending on the subfield, you realize that one input is better than another. Thus you change and refine the weightings in the training phase. In the exam, you will know exactly which of the three you have to turn to in order to get the correct result.
This is exactly what all neurons in the network do. They are given a certain number of inputs during training, depending on how many neurons are “sitting” in close proximity. During training, they decide at each step which preliminary result is best for them and then compare it to the actual result to see if they were right. After training, i.e., in the exam, they then know exactly which prior neurons are the most important.
What is the Loss Function?
The goal of artificial neural networks is to reduce the difference between the self-predicted result and the actual result in reality with each training step. In order to achieve this goal and to be able to track the way there, there is the so-called loss function. It provides a mathematical statement about how far the network’s response is from the desired, actual response.
In the optimal case, the loss function has a value of 0, because then the result of artificial neural networks exactly matches the actual result. Thus, in each training step, an attempt is made to approximate the loss function to the value 0. In order to find the minimum of the loss function and to approach it quickly, gradient descent is used, for example.
Which Applications use Artificial Neural Networks?
Neural Networks are based on perceptrons and are mainly used in the field of Machine Learning. The goal here is mainly to learn structures in previous data and then predict new values. Some examples are:
- Object Recognition in Images: Artificial Neural Networks can recognize objects in images or assign images to a class. Companies use this property in autonomous driving, for example, to recognize objects to which the car should react. Another area of application is in medicine when X-ray images are to be examined to detect an early stage of cancer, for example.
- Prediction: If companies are able to predict future scenarios or states very accurately, they can weigh different decision options well against each other and choose the best option. For example, high-quality regression analysis for expected sales in the next year can be used to decide how much budget to allocate to marketing.
- Customer Sentiment Analysis: Through the Internet, customers have many channels to make their reviews of the brand or a product public. Therefore, companies need to keep track of whether customers are mostly satisfied or not. With a few reviews, which are classified as good or bad, efficient models can be trained, which can then automatically classify a large number of comments.
- Spam Detection: In many mail programs there is the possibility to mark concrete emails as spam. This data is used to train Machine Learning models that directly mark future emails as spam so that the end user does not even see them.
- Analysis of Stock Prices: Neural Networks can also be used to predict the development of a stock based on previous stock prices. Various influencing variables play a role here, such as the overall economic situation or new information about the company.
This is what you should take with you
- Artificial neural networks consist of a large number of neurons. The weight of the individual neurons is changed and refined during the training phase.
- The network is composed of three different layer types: Input layer, hidden layer, and output layer.
- The goal of artificial neural networks is to minimize the loss function, i.e. the difference between the predicted result and the actual result.
What is a Boltzmann Machine?
Unlocking the Power of Boltzmann Machines: From Theory to Applications in Deep Learning. Explore their role in AI.
What is the Gini Impurity?
Explore Gini impurity: A crucial metric shaping decision trees in machine learning.
What is the Hessian Matrix?
Explore the Hessian matrix: its math, applications in optimization & machine learning, and real-world significance.
What is Early Stopping?
Master the art of Early Stopping: Prevent overfitting, save resources, and optimize your machine learning models.
What is RMSprop?
Master RMSprop optimization for neural networks. Explore RMSprop, math, applications, and hyperparameters in deep learning.
What is the Conjugate Gradient?
Explore Conjugate Gradient: Algorithm Description, Variants, Applications and Limitations.
Other Articles on the Topic of Artificial Neural Networks
- Here you can follow the training of artificial neural networks step by step with real values.

Niklas Lang
I have been working as a machine learning engineer and software developer since 2020 and am passionate about the world of data, algorithms and software development. In addition to my work in the field, I teach at several German universities, including the IU International University of Applied Sciences and the Baden-Württemberg Cooperative State University, in the fields of data science, mathematics and business analytics.
My goal is to present complex topics such as statistics and machine learning in a way that makes them not only understandable, but also exciting and tangible. I combine practical experience from industry with sound theoretical foundations to prepare my students in the best possible way for the challenges of the data world.





