Im Bereich der Optimierung, wo das Streben nach dem bestmöglichen Ergebnis im Vordergrund steht, ist das Konzept der Line Search ein grundlegendes und unverzichtbares Werkzeug. Die Line Search ist im Wesentlichen die Kunst, beim Durchqueren der mehrdimensionalen Landschaft einer Zielfunktion die optimale Schrittgröße oder Länge entlang einer bestimmten Richtung zu finden. Sie spielt in zahlreichen Optimierungsalgorithmen eine zentrale Rolle, da sie ihnen eine effiziente und effektive Konvergenz ermöglicht.

Die Liniensuche versucht, eine entscheidende Frage zu beantworten: Wie weit sollte man sich in eine bestimmte Richtung bewegen, um eine optimalere Lösung zu erreichen? Die Antwort auf diese Frage hängt von verschiedenen Faktoren ab, unter anderem von der Art des Optimierungsproblems, der Wahl der Optimierungsmethode und den Eigenschaften der Zielfunktion.

Dieser Artikel begibt sich auf eine Reise, um die Feinheiten der Line Search in der Optimierung zu erkunden. Wir befassen uns mit ihrer Motivation, ihren Grundprinzipien und den verschiedenen Methoden und Bedingungen, die zur Bestimmung der Schrittgrößen verwendet werden. Auf dem Weg dorthin werden wir praktische Beispiele und Einblicke in die Anwendungen bei der Lösung von Problemen in der realen Welt erhalten. Ganz gleich, ob Du ein Anfänger bist, der eine Einführung in die Optimierung sucht, oder ein erfahrener Optimierer, der seine Techniken verfeinern möchte, diese Erkundung der Zeilensuche wird einen Schlüsselaspekt auf dem Weg zur Optimierung beleuchten.

Was ist die Line Search in der Optimierung?

Die Line Search ist eine grundlegende Technik, die in der Optimierung verwendet wird, um die ideale Schrittgröße oder -länge bei der Aktualisierung der Lösung während einer iterativen Suche nach dem optimalen Ergebnis zu bestimmen. Im mehrdimensionalen Raum der Optimierungsprobleme dient sie als Leitfaden, der den Optimierungsalgorithmen hilft, sich im Terrain der Zielfunktion zurechtzufinden.

Die Kernidee der Line Search besteht darin, den Sweet Spot – die Schrittgröße – zu finden, die die größte Verbesserung der Zielfunktion bringt, während man sich von der aktuellen Lösung zu einer neuen Lösung bewegt. Diese Suche nach der optimalen Schrittgröße ist für Optimierungsalgorithmen entscheidend, um effizient und effektiv konvergieren zu können.

Die Wahl der Schrittweite beeinflusst die Geschwindigkeit und den Erfolg der Optimierung. Ist die Schrittweite zu klein, kann die Optimierung nur langsam konvergieren, während eine zu große Schrittweite zum Überschreiten der optimalen Lösung oder sogar zur Divergenz führen kann.

Liniensuchmethoden stützen sich auf Bedingungen, die oft auf dem Gradienten der Zielfunktion basieren, um die Suche nach der idealen Schrittgröße zu leiten. Diese Bedingungen stellen sicher, dass die gewählte Schrittgröße zu einer ausreichenden Verringerung der Zielfunktion führt und mit dem Optimierungsziel übereinstimmt.

Die Line Search ist keine Einheitsmethode, sondern passt sich den spezifischen Merkmalen des Optimierungsproblems und der gewählten Optimierungsmethode an. Verschiedene Bedingungen und Strategien, wie die Armijo-Wolfe-Bedingungen, die Goldstein-Bedingungen oder die Strong-Wolfe-Bedingungen, helfen bei der Bestimmung der Schrittweite unter verschiedenen Bedingungen.

Insgesamt ist die Line Search ein zentraler Bestandteil von Optimierungsalgorithmen, der sie zum gewünschten Ergebnis führt und gleichzeitig den Kompromiss zwischen schneller Konvergenz und dem Risiko des Überschießens effizient bewältigt. Sie spielt eine entscheidende Rolle in einer Vielzahl von Bereichen, vom maschinellen Lernen und der numerischen Analyse bis hin zu wissenschaftlichen Simulationen und technischem Design. Die Kunst der Liniensuche zu verstehen und zu beherrschen ist der Schlüssel zum Erfolg in der Welt der Optimierung.

Welche grundlegenden Line Search Methoden gibt es?

Im Bereich der Optimierung ist diese Suchmethode entscheidend für die Bestimmung der idealen Schrittgröße oder -länge während des iterativen Prozesses auf dem Weg zur optimalen Lösung. Diese Methoden stützen sich auf bestimmte Bedingungen und Kriterien, um die Suche nach der am besten geeigneten Schrittlänge zu leiten. In diesem Abschnitt werden wir einige grundlegende Methoden der Line Search untersuchen, darunter die Armijo-Wolfe-Bedingungen, die Goldstein-Bedingung und die Wolfe-Powell-Bedingungen, und untersuchen, wie sie zum Optimierungsprozess beitragen.

Armijo-Wolfe-Bedingungen:

• Die Armijo-Wolfe-Bedingungen, die auch als Armijo-Regel bekannt sind, bilden einen weit verbreiteten Rahmen für die Line Search. Sie stellen sicher, dass die neue Lösung eine ausreichende Verringerung des Zielfunktionswertes bietet. Diese Bedingungen bestehen aus zwei Hauptkriterien:
  • Ausreichende Verminderungsbedingung: Sie stellt sicher, dass die Zielfunktion um einen bestimmten Anteil (in der Regel einen kleinen Bruchteil) der erwarteten Abnahme abnimmt, die durch die lineare Approximation der Funktion vorhergesagt wird.
  • Krümmungsbedingung: Mit dieser Bedingung wird überprüft, ob die Steigung oder der Gradient der Zielfunktion mit der Suchrichtung übereinstimmt, was darauf hindeutet, dass die Schrittgröße angemessen ist.

Goldstein-Bedingung:

• Die Goldstein-Bedingung ist eine weitere Methode zur Bewertung der Akzeptanz einer gewählten Schrittgröße. Sie prüft, ob die erzielte Verringerung der Zielfunktion innerhalb eines bestimmten Bereichs zwischen der vorhergesagten Verringerung und einem bestimmten Schwellenwert liegt. Diese Bedingung erhöht die Flexibilität und kann dazu beitragen, eine zu konservative Wahl der Schrittgröße zu verhindern.

Wolfe-Powell-Bedingungen:

• Bei den Wolfe-Powell-Bedingungen handelt es sich um eine Reihe von Bedingungen, die sowohl eine ausreichende Abnahme als auch eine ausreichende Krümmung der Zielfunktion gewährleisten sollen. Sie bestehen aus zwei Hauptbedingungen:
  • Ausreichende Abnahmebedingung: Ähnlich wie die Armijo-Bedingung prüft diese Wolfe-Powell-Bedingung, dass der Funktionswert um einen bestimmten Anteil abnimmt.
  • Krümmungsbedingung: Mit dieser Bedingung wird der Winkel zwischen dem Gradientenvektor und der Suchrichtung bewertet, um sicherzustellen, dass die Schrittgröße mit der Abstiegsrichtung übereinstimmt.

Diese grundlegenden Methoden der Liniensuche spielen in Optimierungsalgorithmen eine entscheidende Rolle, da sie einen systematischen Ansatz für die Auswahl geeigneter Schrittgrößen bieten. Je nach Optimierungsproblem kann die Wahl der Bedingungen und Methoden variieren. Diese Methoden sind ein wichtiger Bestandteil des Optimierungswerkzeugkastens und stellen sicher, dass der Weg zu einer optimalen Lösung effizient und effektiv verläuft.

Wie kann die Line Search in den Gradientenabstieg integriert werden?

Die Line Search ist ein unverzichtbarer Begleiter von Optimierungsalgorithmen wie dem Gradientenabstieg. Sie spielt eine zentrale Rolle bei der Feinabstimmung der Schrittgrößen, um die mehrdimensionale Landschaft der Zielfunktionen effektiv zu durchqueren. In diesem Abschnitt wird erläutert, wie diese Suchmethode nahtlos in den Gradientenabstieg und andere Optimierungsmethoden integriert werden kann, um sicherzustellen, dass jeder Schritt den Algorithmus näher an die optimale Lösung bringt.

1. Gradientenabstieg und Schrittweiten:

Der Gradientenabstieg, ein weit verbreiteter Optimierungsalgorithmus, stützt sich auf den Gradienten oder die Ableitung der Zielfunktion, um die Richtung des steilsten Abstiegs zu bestimmen. Die Schrittweite wird dabei jedoch nicht festgelegt. An dieser Stelle kommt die Line Search ins Spiel.

Sie hilft Gradientenabstiegsalgorithmen bei der Beantwortung der entscheidenden Frage: “Wie groß sollte jeder Schritt sein?” Die Antwort ist nicht allgemeingültig und hängt von den lokalen Merkmalen der Zielfunktion ab.

2. Bestimmung der Schrittgröße:

Beim Gradientenabstieg hat die gewählte Schrittgröße Auswirkungen auf die Effizienz und den Erfolg des Optimierungsprozesses. Ist die Schrittgröße zu klein, konvergiert der Algorithmus möglicherweise nur sehr langsam, während eine zu große Schrittgröße zu einem Überschießen der optimalen Lösung führen kann.

Methoden der Liniensuche wie die Armijo-Wolfe-Bedingungen, die Goldstein-Bedingungen und die Wolfe-Powell-Bedingungen unterstützen den Gradientenabstieg bei der Auswahl einer geeigneten Schrittgröße, die ein Gleichgewicht zwischen schneller Konvergenz und der Vermeidung von Überschwingen herstellt.

3. Praktische Beispiele:

Betrachten wir ein praktisches Beispiel: das Training eines maschinellen Lernmodells. Im Kontext des stochastischen Gradientenabstiegs (SGD) hilft die Line Search, die Lernrate bei jedem Schritt anzupassen, um eine effiziente Konvergenz während des Trainingsprozesses sicherzustellen.

Durch den Einsatz der Line Search innerhalb des SGD passt sich der Algorithmus an die sich verändernde Landschaft der Verlustfunktion an und verwaltet die Lernrate effektiv, um sicherzustellen, dass die Modellparameter zu einem optimalen Zustand konvergieren.

4. Visualisierung der Liniensuche in Aktion:

Um die Bedeutung der Line Search beim Gradientenabstieg zu begreifen, stelle Dir einen Wanderer vor, der durch ein zerklüftetes Gelände wandert. Das Gelände stellt die Zielfunktion dar, und der Wanderer möchte den niedrigsten Punkt (die optimale Lösung) erreichen. Die Line Search hilft dem Wanderer bei der Wahl der idealen Schrittgröße an jedem Punkt und führt ihn effizient in Richtung Tal, wobei steile Klippen und Schluchten vermieden werden.

Zusammenfassend lässt sich sagen, dass Line Search und Gradientenabstieg ein dynamisches Duo in der Welt der Optimierung sind. Die Liniensuche fügt dem Gradientenabstieg eine entscheidende Ebene der Intelligenz hinzu, die ihn an unterschiedliche Landschaften anpassungsfähig macht und letztlich sicherstellt, dass der Optimierungsprozess sein Ziel – die optimale Lösung – effizient und effektiv erreicht.

Wie werden die Newtonsche Methode und die Line Search kombiniert?

Im Bereich der Optimierung, insbesondere bei nichtlinearen Problemen, ist die Newton-Methode ein leistungsfähiges Werkzeug, um lokale Optima effizient zu finden. Um jedoch sicherzustellen, dass die Methode genau konvergiert und nicht über das Ziel hinausschießt, werden häufig Techniken der Line Search eingesetzt. In diesem Abschnitt werden wir untersuchen, wie die Line Search und die Newton-Methode zusammenarbeiten, um komplexe Optimierungsprobleme zu bewältigen.

1. Überblick über die Newton-Methode:

Die Newton-Methode ist bekannt für ihre schnelle Konvergenz beim Auffinden lokaler Minima oder Maxima. Sie nutzt Informationen zweiter Ordnung über die Zielfunktion, indem sie die Hessian-Matrix berücksichtigt, die die Krümmung der Oberfläche der Funktion beschreibt.

Während die Newton-Methode in der Theorie effizient ist, kann die Wahl der Schrittgröße ihre Leistung erheblich beeinträchtigen, insbesondere in Regionen mit starken Veränderungen in der Funktion.

2. Die Rolle der Liniensuche:

Techniken der Line Search helfen, die Herausforderung der Wahl geeigneter Schrittgrößen innerhalb der Newton-Methode zu bewältigen. Da sich die Methode auf die Krümmung der Funktion stützt, muss sichergestellt werden, dass die unternommenen Schritte mit dem Ziel, eine optimale Lösung zu erreichen, übereinstimmen.

3. Adaptive Schrittgrößen:

Während der Ausführung der Newton-Methode ermöglicht die Line Search die Anpassung der Schrittgrößen bei jeder Iteration. Diese Anpassungsfähigkeit stellt sicher, dass der Algorithmus stabil bleibt und auch in Regionen, in denen die Krümmung der Funktion stark variiert, effektiv konvergiert.

4. Verhinderung des Überschreitens:

Die Newton-Methode mit ihrer hohen Konvergenzrate kann dazu neigen, über die optimale Lösung hinauszuschießen, wenn die Schrittgrößen nicht sorgfältig verwaltet werden. Line Search Methoden wie die Armijo-Wolfe-Bedingungen und Wolfe-Powell-Bedingungen helfen bei der Kontrolle der Schrittgrößen, um dieses Problem zu vermeiden.

5. Praktische Anwendungen:

Die Newton-Methode mit Zeilensuche findet in vielen Bereichen Anwendung, darunter Physik, Ingenieurwesen und maschinelles Lernen. Beim maschinellen Lernen wird sie zum Trainieren von Modellen verwendet, bei denen es entscheidend ist, die optimalen Parameterwerte zu finden.

6. Visualisierung der Partnerschaft:

Stellen Dir vor, Du navigierst durch eine hügelige Landschaft und musst den tiefsten Punkt erreichen. Die Newton-Methode ist wie ein leistungsfähiges Fahrzeug mit einem fortschrittlichen GPS-System (das Informationen zweiter Ordnung nutzt), während die Line Search als intelligenter Fahrer fungiert, der das Gaspedal sorgfältig einstellt, um einen reibungslosen und sicheren Abstieg zu gewährleisten.

Zusammenfassend lässt sich sagen, dass die Zusammenarbeit zwischen der Line Search und der Newton-Methode ein Beweis für die Synergie zwischen Optimierungstechniken ist. Sie ermöglicht die effiziente Untersuchung komplexer, nichtlinearer Probleme durch Optimierung der Schrittgrößen, was zu schneller Konvergenz und genauer Lösungsfindung führt.

Was ist Backtracking der Line Search?

Die Backtracking Line Search ist eine wertvolle Technik, die in Optimierungsalgorithmen eingesetzt wird, um die Schrittgrößen während der iterativen Suche nach einer optimalen Lösung dynamisch anzupassen. Mit diesem Ansatz wird sichergestellt, dass sich der Algorithmus mit jedem Schritt im Optimierungsprozess der Lösung nähert und dabei bestimmte Bedingungen erfüllt. In diesem Abschnitt werden wir uns mit dem Konzept und ihrer Bedeutung für die Optimierung befassen.

1. Motivation für Backtracking:

• In vielen Optimierungsszenarien kann die Bestimmung einer geeigneten festen Schrittgröße eine Herausforderung darstellen. Eine zu große Schrittgröße kann zu einem Überschießen der optimalen Lösung führen, während eine zu kleine Schrittgröße den Konvergenzprozess verlangsamen kann.
• Die Backtracking-Line Search löst dieses Problem, indem sie es dem Optimierungsalgorithmus ermöglicht, die Schrittgröße anhand bestimmter Kriterien adaptiv zu bestimmen.

2. Dynamische Schrittgrößenanpassung:

• Die Backtracking-Line Search passt die Schrittgröße dynamisch an, indem sie die Änderungsrate der Zielfunktion berücksichtigt, die oft als Steigung oder Gradient bezeichnet wird.

• Sie bietet eine systematische Möglichkeit, die Schrittgröße bei Bedarf zu verringern, um sicherzustellen, dass sich der Algorithmus mit jeder Iteration der optimalen Lösung nähert.

3. Grundprinzipien:

• Die Backtracking-Zeilensuche beruht in der Regel auf den folgenden Grundprinzipien:
  • Man beginnt mit einer anfänglichen Schrittgröße, die im Laufe des Algorithmus angepasst werden kann.
  • Bewertung der Zielfunktion am aktuellen Punkt und am potenziellen nächsten Punkt mit der angepassten Schrittgröße.
  • Vergleiche die Werte der Zielfunktion mit bestimmten Kriterien, z. B. der Armijo-Bedingung oder der Wolfe-Bedingung.
  • Wenn die Kriterien erfüllt sind, wird die Schrittgröße als angemessen betrachtet; andernfalls wird sie verringert und der Prozess wird wiederholt, bis eine geeignete Schrittgröße gefunden ist.

4. Verhinderung von Überschreitungen:

Die Backtracking-Line Search ist besonders wirksam bei der Verhinderung des Überschwingens, das bei einer zu großen Schrittgröße auftreten kann. Durch die Bewertung der Kriterien stellt der Algorithmus sicher, dass die Schrittgröße den lokalen Eigenschaften der Zielfunktion angemessen ist.

5. Allgemeine Verwendung:

Die Backtracking-Line Search wird häufig in Optimierungsalgorithmen wie dem Gradientenabstieg und der Newton-Methode zur Feinabstimmung der Schrittgröße verwendet. Sie spielt eine entscheidende Rolle für deren Konvergenz und Stabilität.

Zusammenfassend lässt sich sagen, dass die Backtracking-Liniensuche ein flexibles und anpassungsfähiges Werkzeug ist, das Optimierungsalgorithmen dabei hilft, fundierte Entscheidungen über Schrittgrößen zu treffen. Es fördert die effiziente Konvergenz und stellt sicher, dass der Optimierungsprozess effektiv zur optimalen Lösung führt und gleichzeitig ein Überschießen oder langsame Fortschritte vermieden werden.

Wie ist die Liniensuche im Vergleich zu anderen Optimierungsalgorithmen?

Die Line Search ist ein grundlegender Bestandteil von Optimierungsalgorithmen, und ihre Aufgabe besteht darin, die Schrittgröße oder Lernrate adaptiv zu bestimmen, um die Konvergenz dieser Algorithmen zu steuern. Vergleichen wir sie mit einigen anderen gängigen Optimierungsverfahren, um ihre Vorteile und Grenzen zu verstehen.

1. Gradientenabstieg:

• Gradientenabstieg mit fester Schrittweite: Beim einfachen Gradientenabstieg wird eine feste Schrittgröße verwendet, was zu einer langsamen Konvergenz oder zum Überschreiten des Minimums führen kann. Die Line Search ermöglicht eine adaptive Auswahl der Schrittgröße, wodurch die Konvergenzgeschwindigkeit verbessert werden kann.
• Gradientenabstieg mit Liniensuche: Wenn diese Suchmethode in den Gradientenabstieg integriert wird, entfällt die Notwendigkeit, die Lernrate manuell einzustellen.

2. Newton-Methode:

• Newton-Methode mit fester Schrittweite: Die Newton-Methode kann schnell konvergieren, erfordert aber eine sorgfältige Auswahl der Schrittgröße, was eine Herausforderung darstellen kann. Die Line Search kann die Schrittgröße dynamisch anpassen, was die Stabilität und die Konvergenzeigenschaften verbessert.

3. Konjugierter Gradient:

• Konjugierter Gradient mit fester Schrittweite: Der konjugierte Gradient ist eine iterative Methode zur Lösung linearer Gleichungssysteme und zur Optimierung quadratischer Funktionen. Feste Schrittgrößen sind bei komplexen Optimierungsproblemen möglicherweise nicht geeignet. Die Liniensuche kann im konjugierten Gradienten zur adaptiven Feinabstimmung der Schrittgrößen verwendet werden.

4. Stochastischer Gradientenabstieg (SGD):

• Stochastischer Gradientenabstieg mit fester Schrittweite: Beim SGD wird eine feste Lernrate verwendet, was bei nicht-konvexen Problemen zu Oszillationen und langsamer Konvergenz führen kann. Die Line Search kann dazu beitragen, die Lernrate an die spezifischen Daten und das Problem anzupassen und so die Konvergenz zu verbessern.

5. Trust Region Methoden:

• Vertrauensregionsmethoden mit adaptiven Regionen: Vertrauensregionsmethoden verwenden vordefinierte Regionen, innerhalb derer die Optimierung stattfindet. Mit Hilfe der Liniensuche können diese Regionen dynamisch angepasst werden, was die Anpassungsfähigkeit und die Konvergenzeigenschaften verbessert.

Vorteile:

• Anpassungsfähigkeit: Die Liniensuche ermöglicht es Optimierungsalgorithmen, Schrittgrößen adaptiv anzupassen, was sie robust und für eine Vielzahl von Problemen geeignet macht.
• Verbesserte Konvergenz: Durch die dynamische Wahl der Schrittgröße kann die Line Search zu einer schnelleren Konvergenz und stabileren Optimierung führen.

Beschränkungen:

• Berechnungsaufwand: Die Line Search ist mit zusätzlichem Rechenaufwand verbunden, um die optimale Schrittgröße zu finden, was bei einfachen Problemen mit festen Schrittgrößen möglicherweise nicht notwendig ist.
• Keine Universallösung: Die Line Search ist zwar leistungsfähig, aber keine Universallösung und eignet sich möglicherweise nicht für jedes Optimierungsproblem.

Zusammenfassend lässt sich sagen, dass die Line Search bei Optimierungsalgorithmen eine entscheidende Rolle spielt, da sie ihnen hilft, sich an komplexe und dynamische Probleme anzupassen. Ihre Fähigkeit, Schrittgrößen dynamisch anzupassen, kann die Konvergenz und Stabilität verschiedener Optimierungsverfahren erheblich verbessern, was sie zu einem wertvollen Werkzeug im Bereich der numerischen Optimierung macht.

Wie kann man die Line Search in Python implementieren?

In Python kannst Du Line Search Techniken implementieren, um die Schrittgrößen in Optimierungsalgorithmen adaptiv anzupassen. Die Line Search ist ein wichtiger Bestandteil vieler Optimierungsmethoden, wie z. B. des Gradientenabstiegs, des konjugierten Gradienten und der Newton-Methode. Im Folgenden werden die grundlegenden Schritte zur Implementierung der Line Search in Python anhand eines einfachen Beispiels erläutert.

1. Objektive Funktion: Beginne mit der Definition der Zielfunktion, die Du optimieren möchtest. Für dieses Beispiel betrachten wir eine einfache quadratische Funktion:

2. Berechnung des Gradienten: Um die Suche effektiv durchzuführen, musst Du den Gradienten Deiner Zielfunktion berechnen. In diesem Fall ist der Gradient der quadratischen Funktion einfach zu berechnen:

3. Line Search Algorithmus: Als nächstes wird der Algorithmus implementiert. Ein gängiger Ansatz ist die Armijo-Wolfe-Bedingung. Hier ist eine vereinfachte Version in Python:

In diesem Code ist alpha die Schrittweite, beta der Reduktionsfaktor und c ein Parameter, der die Bedingung für eine ausreichende Reduktion der Zielfunktion festlegt.

4. Anwenden der Line Search: Du kannst den Algorithmus nun innerhalb Deines Optimierungsalgorithmus anwenden. Hier ist ein einfaches Beispiel für die Anwendung im Gradientenabstieg:

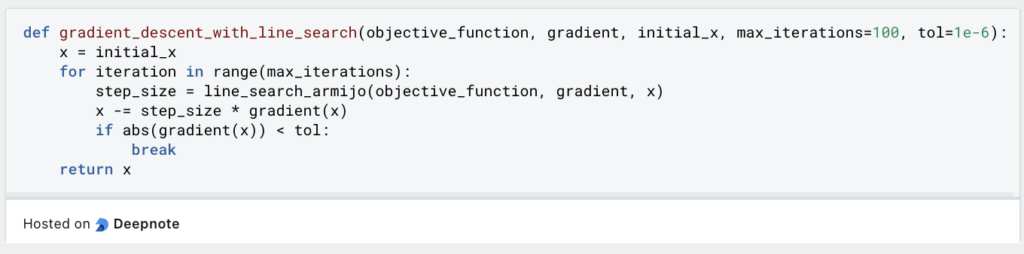
5. Ausführen der Optimierung: Schließlich kannst Du Deinen Optimierungsalgorithmus mit der Line Search ausführen:

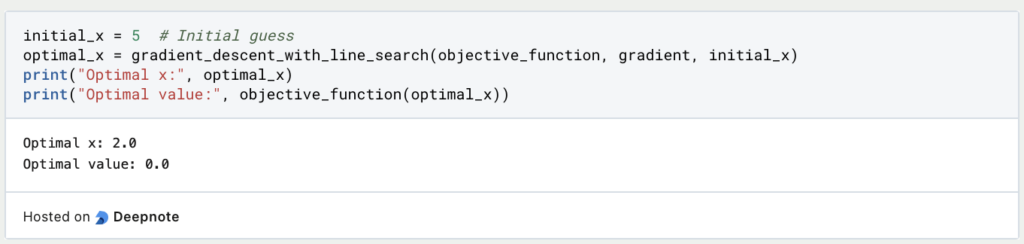
Dieses Beispiel zeigt, wie man eine einfache Line Search in Python implementiert und sie im Kontext des Gradientenabstiegs anwendet. Dies ist eine vielseitige Technik, die an verschiedene Optimierungsalgorithmen angepasst werden kann, was sie zu einem wertvollen Werkzeug in der numerischen Optimierung macht.

Das solltest Du mitnehmen

• Die Line Search ist ein grundlegender Bestandteil von Optimierungsalgorithmen, der die adaptive Auswahl von Schrittgrößen während des Optimierungsprozesses steuert.
• Sie bietet Anpassungsfähigkeit und verbessert die Konvergenz und Stabilität in einem breiten Spektrum von Optimierungsproblemen.
• Im Vergleich zu festen Schrittgrößen bietet die Liniensuche verbesserte Konvergenzeigenschaften und Anpassungsfähigkeit.
• Die Line Search kann mit Optimierungstechniken wie Gradientenabstieg, Newton-Methode, konjugiertem Gradienten, stochastischem Gradientenabstieg und Vertrauensbereichsverfahren kombiniert werden.
• Die Line Search ist zwar vorteilhaft, führt aber zu einem zusätzlichen Rechenaufwand im Optimierungsprozess.
• Sie ist keine Universallösung und eignet sich möglicherweise nicht für alle Optimierungsprobleme.
• Das Verständnis und die Umsetzung der Zeilensuche sind für Praktiker im Bereich der numerischen Optimierung von wesentlicher Bedeutung.

Andere Beiträge zum Thema Line Search

Hier findest Du die Dokumentation, wie Du eine Zeilensuche in SciPy durchführen kannst.