What is the Line Search?

In the realm of optimization, where the pursuit of the best possible outcome is paramount, the concept of line search stands as a fundamental and indispensable tool. Line search, in its essence, is the art of finding the optimal step size or length along a given direction when traversing the multidimensional landscape of an objective function. It plays a pivotal role in numerous optimization algorithms, enabling them to converge efficiently and effectively.

Line search seeks to answer a critical question: How far should we move in a particular direction to reach a more optimal solution? The answer to this question depends on various factors, including the nature of the optimization problem, the choice of optimization method, and the characteristics of the objective function.

This article embarks on a journey to explore the intricacies of line search in optimization. We will delve into its motivation, basic principles, and the various methods and conditions used to determine step sizes. Along the way, we will encounter practical examples and insights into its applications in real-world problem-solving. Whether you are a novice seeking an introduction to optimization or a seasoned optimizer looking to refine your techniques, this exploration of line search will shed light on a key aspect of the quest for optimization excellence.

What is Line Search in Optimization?

A line search is a fundamental technique used in optimization to determine the ideal step size or length when updating the solution during an iterative search for the optimal result. In the multidimensional space of optimization problems, it acts as a guide, helping optimization algorithms navigate the terrain of the objective function.

The core idea of a line search is to find the sweet spot – the step size – that brings the most significant improvement in the objective function while moving from the current solution to a new one. This search for the optimal step size is critical for optimization algorithms to achieve convergence efficiently and effectively.

The choice of step size affects the speed and success of optimization. If the step size is too small, the optimization may converge slowly, while an excessively large step size can lead to overshooting the optimal solution or even divergence.

Line search methods rely on conditions, often based on the gradient of the objective function, to guide the search for the ideal step size. These conditions ensure that the selected step size results in a sufficient reduction in the objective function, aligning with the optimization goal.

Line search is not a one-size-fits-all technique; it adapts to the specific characteristics of the optimization problem and the chosen optimization method. Different conditions and strategies, such as the Armijo-Wolfe conditions, Goldstein conditions, or Strong Wolfe conditions, help determine the step size under varying circumstances.

Overall, a line search is a pivotal component of optimization algorithms, guiding them toward the desired outcome while efficiently managing the trade-off between rapid convergence and the risk of overshooting. It plays a crucial role in a wide range of fields, from machine learning and numerical analysis to scientific simulations and engineering design. Understanding and mastering the art of line search is key to achieving success in the world of optimization.

What are the basic Line Search methods?

In the realm of optimization, this search method is crucial for determining the ideal step size or length during the iterative process of moving toward the optimal solution. These methods rely on specific conditions and criteria to guide the search for the most suitable step length. In this section, we will explore some fundamental line search methods, including the Armijo-Wolfe conditions, the Goldstein condition, and the Wolfe-Powell conditions, and delve into how they contribute to the optimization process.

Armijo-Wolfe Conditions:

The Armijo-Wolfe conditions, also known as the Armijo rule, provide a widely used framework for line search. They focus on ensuring that the new solution offers a sufficient reduction in the objective function value. These conditions consist of two main criteria:
- Sufficient Decrease Condition: It ensures that the objective function decreases by a certain proportion (usually a small fraction) of the expected decrease predicted by the linear approximation of the function.
- Curvature Condition: This condition checks that the slope or gradient of the objective function aligns with the search direction, indicating that the step size is appropriate.

Goldstein Condition:

The Goldstein condition is another method for evaluating the acceptability of a chosen step size. It checks if the achieved reduction in the objective function falls within a specified range between the predicted decrease and a certain threshold. This condition adds flexibility and can help prevent overly conservative step size choices.

Wolfe-Powell Conditions:

The Wolfe-Powell conditions are a set of conditions used to ensure both sufficient decrease and curvature in the objective function. They comprise two primary conditions:
- Sufficient Decrease Condition: Similar to the Armijo condition, this Wolfe-Powell condition checks that the function value decreases by a specified proportion.
- Curvature Condition: This condition assesses the angle between the gradient vector and the search direction, ensuring that the step size aligns with the descent direction.

These basic line search methods play a critical role in optimization algorithms, offering a systematic approach to selecting appropriate step sizes. Depending on the optimization problem, the choice of conditions and methods may vary. These methods are a vital part of the optimization toolbox, ensuring that the journey towards an optimal solution proceeds efficiently and effectively.

How can the Line Search be integrated into Gradient Descent?

Line search is an essential companion to optimization algorithms like gradient descent, playing a pivotal role in fine-tuning step sizes to navigate the multidimensional landscape of objective functions effectively. In this section, we’ll delve into how this search method is seamlessly integrated with gradient descent and other optimization methods, ensuring that each step brings the algorithm closer to the optimal solution.

1. Gradient Descent and Step Sizes:

Gradient descent, a widely used optimization algorithm, relies on the gradient or derivative of the objective function to determine the direction of the steepest descent. However, it doesn’t specify the step size. This is where line search comes into play.
It helps gradient descent algorithms answer the critical question: “How large should each step be?” The answer is not universal and depends on the local characteristics of the objective function.

2. Step Size Determination:

In gradient descent, the chosen step size impacts the efficiency and success of the optimization process. If the step size is too small, the algorithm might converge very slowly, while a step that’s too large can lead to overshooting the optimal solution.
Line search methods, such as the Armijo-Wolfe conditions, Goldstein conditions, and Wolfe-Powell conditions, assist gradient descent in selecting an appropriate step size that balances rapid convergence and avoids overshooting.

3. Practical Examples:

Let’s consider a practical example: training a machine learning model. In the context of stochastic gradient descent (SGD), line search helps adjust the learning rate at each step to ensure efficient convergence during the training process.
By employing line search within SGD, the algorithm adapts to the changing landscape of the loss function, effectively managing the learning rate to ensure that model parameters converge to an optimal state.

4. Visualizing Line Search in Action:

To grasp the significance of line search in gradient descent, imagine a hiker navigating a rugged terrain. The terrain represents the objective function, and the hiker aims to reach the lowest point (the optimal solution). It helps the hiker choose the ideal step size at each point, guiding them efficiently towards the valley while avoiding steep cliffs and ravines.

In summary, line search and gradient descent are a dynamic duo in the world of optimization. Line search adds a critical layer of intelligence to gradient descent, making it adaptable to diverse landscapes, and ultimately ensuring that the optimization process reaches its destination – the optimal solution – efficiently and effectively.

How are Newton’s Method and Line Search combined?

In the realm of optimization, particularly for nonlinear problems, Newton’s method is a powerful tool for finding local optima efficiently. However, to ensure that the method converges accurately and avoids overshooting the target, it often relies on line search techniques. In this section, we will explore how line search and Newton’s method work in tandem to tackle complex optimization challenges.

1. Newton’s Method Overview:

Newton’s method is known for its rapid convergence in finding local minima or maxima. It utilizes second-order information about the objective function by considering the Hessian matrix, which describes the curvature of the function’s surface.
While Newton’s method is efficient in theory, the choice of step size can significantly impact its performance, particularly in regions with sharp changes in the function.

2. The Role of Line Search:

Line search techniques help address the challenge of choosing appropriate step sizes within Newton’s method. Since the method relies on the curvature of the function, it’s crucial to ensure that steps taken align with the objective of reaching an optimal solution.

3. Adaptive Step Sizes:

During the execution of Newton’s method, line search allows for the adaptation of step sizes at each iteration. This adaptability ensures that the algorithm remains stable and converges effectively even in regions where the curvature of the function varies significantly.

4. Preventing Overshooting:

Newton’s method, with its high convergence rate, can be prone to overshooting the optimal solution if step sizes are not carefully managed. Line search methods, such as the Armijo-Wolfe conditions and Wolfe-Powell conditions, help in controlling the step sizes to prevent this issue.

5. Practical Applications:

Newton’s method with line search finds applications in a wide range of fields, including physics, engineering, and machine learning. In machine learning, it is utilized for training models where finding the optimal parameter values is crucial.

6. Visualizing the Partnership:

Imagine navigating a hilly landscape where you need to reach the lowest point. Newton’s method is like a powerful vehicle with an advanced GPS system (utilizing second-order information), while line search acts as the intelligent driver, carefully adjusting the throttle to ensure a smooth and safe descent.

In conclusion, the collaboration between line search and Newton’s method is a testament to the synergy between optimization techniques. It allows for the efficient exploration of complex, nonlinear problems by optimizing step sizes, resulting in swift convergence and accurate solution finding.

What is Backtracking the Line Search?

Backtracking line search is a valuable technique employed in optimization algorithms to dynamically adjust step sizes during the iterative search for an optimal solution. This approach ensures that each step in the optimization process moves the algorithm closer to the solution while satisfying specific conditions. In this section, we’ll delve into the concept of backtracking line search and its significance in optimization.

1. Motivation for Backtracking:

In many optimization scenarios, determining an appropriate fixed step size can be challenging. A step size that is too large may lead to overshooting the optimal solution, while one that is too small may slow down the convergence process.
Backtracking line search addresses this issue by allowing the optimization algorithm to adaptively determine the step size based on certain criteria.

2. Dynamic Step Size Adjustment:

Backtracking line search dynamically adjusts the step size by considering the rate of change of the objective function, often referred to as the slope or gradient.
It provides a systematic way to reduce the step size when necessary to ensure that each iteration moves the algorithm closer to the optimal solution.

3. Core Principles:

Backtracking line search typically involves the following core principles:
- Start with an initial step size, which can be adjusted as the algorithm progresses.
- Evaluate the objective function at the current point and the potential next point with the adjusted step size.
- Compare the objective function values to specific criteria, such as the Armijo condition or the Wolfe condition.
- If the criteria are met, the step size is considered appropriate; otherwise, it is reduced and the process is repeated until a suitable step size is found.

4. Preventing Overshooting:

Backtracking line search is particularly effective in preventing overshooting, which can occur when the step size is too large. By evaluating the criteria, the algorithm ensures that the step size is appropriate for the local characteristics of the objective function.

5. Common Usage:

Backtracking line search is commonly used in optimization algorithms like gradient descent and Newton’s method to fine-tune the step size. It plays a crucial role in their convergence and stability.

6. Visualizing the Process:

Think of backtracking line search as a dynamic speed controller for a vehicle navigating a curvy road. If the road ahead is steep and winding, the controller will slow down the vehicle to ensure safety and a smooth journey.

In summary, backtracking line search is a flexible and adaptive tool that aids optimization algorithms in making informed decisions about step sizes. It promotes efficient convergence and ensures that the optimization process is effective in reaching the optimal solution while avoiding overshooting or slow progress.

How does Line Search compare to other Optimization Algorithms?

Line search is a fundamental component of optimization algorithms, and its role is to adaptively determine the step size or learning rate to guide the convergence of these algorithms. Let’s compare it with some other common optimization techniques to understand its advantages and limitations.

1. Gradient Descent:

Gradient Descent with Fixed Step Size: In basic gradient descent, a fixed step size is used, which may lead to slow convergence or overshooting the minimum. Line search allows for adaptive step size selection, potentially improving convergence speed.
Gradient Descent with Line Search: When this search method is integrated with gradient descent, it helps avoid the need to manually set the learning rate.

2. Newton’s Method:

Newton’s Method with Fixed Step Size: Newton’s method can converge rapidly but requires careful selection of the step size, which may be challenging. Line search can dynamically adjust the step size, improving stability and convergence properties.

3. Conjugate Gradient:

Conjugate Gradient with Fixed Step Size: Conjugate gradient is an iterative method for solving systems of linear equations and optimizing quadratic functions. Fixed step sizes may not be suitable in complex optimization problems. Line search can be used in conjugate gradient to fine-tune step sizes adaptively.

4. Stochastic Gradient Descent (SGD):

Stochastic Gradient Descent with Fixed Step Size: In SGD, a fixed learning rate is used, which can lead to oscillations and slow convergence in non-convex problems. Line search can help adapt the learning rate to the specific data and problem, improving convergence.

5. Trust Region Methods:

Trust Region Methods with Adaptive Regions: Trust region methods use predefined regions within which optimization occurs. Line search can be used to dynamically adjust these regions, improving adaptability and convergence properties.

Advantages:

Adaptability: Line search allows optimization algorithms to adaptively adjust step sizes, making them robust and suitable for a wide range of problems.
Improved Convergence: By dynamically choosing the step size, line search can lead to faster convergence and more stable optimization.

Limitations:

Computational Overhead: Line search involves additional computational overhead to find the optimal step size, which may not be necessary in simple problems with fixed step sizes.
Not a Universal Solution: While powerful, line search is not a one-size-fits-all solution and may not be suitable for every optimization problem.

In summary, line search plays a crucial role in optimization algorithms, helping them adapt to complex and dynamic problems. Its ability to dynamically adjust step sizes can significantly improve the convergence and stability of various optimization techniques, making it a valuable tool in the field of numerical optimization.

How can you implement the Line Search in Python?

In Python, you can implement line search techniques to adaptively adjust step sizes in optimization algorithms. It is a critical component of many optimization methods, such as gradient descent, conjugate gradient, and Newton’s method. Here, we’ll outline the basic steps for implementing line search in Python using a simple example.

1. Objective Function: Start by defining the objective function that you want to optimize. For this example, let’s consider a simple quadratic function:

2. Gradient Computation: To perform the search effectively, you need to compute the gradient of your objective function. In this case, the gradient of the quadratic function is straightforward:

3. Line Search Algorithm: Next, implement the algorithm. One common approach is the Armijo-Wolfe condition. Here’s a simplified version in Python:

In this code, alpha is the step size, beta is the reduction factor, and c is a parameter that determines the condition for sufficient reduction in the objective function.

4. Applying Line Search: You can now apply the algorithm within your optimization algorithm. Here’s a simple example of using it in gradient descent:

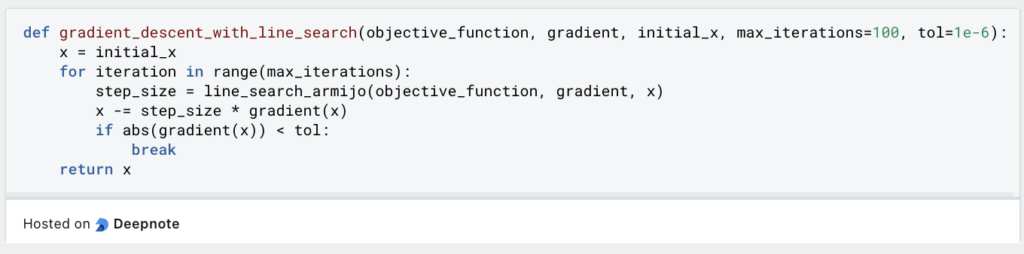
5. Running the Optimization: Finally, you can run your optimization algorithm with the line search:

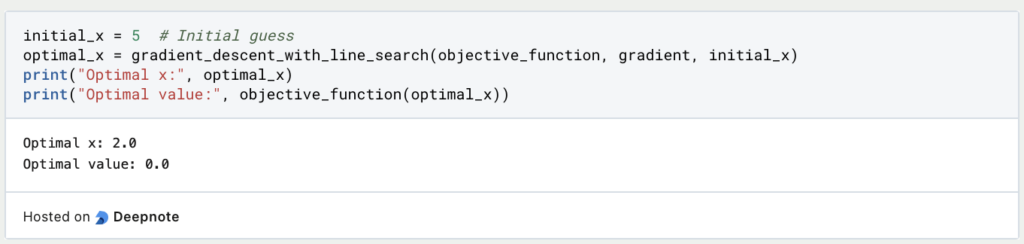
This example demonstrates how to implement a basic line search in Python and apply it in the context of gradient descent. This is a versatile technique that can be adapted to various optimization algorithms, making it a valuable tool in numerical optimization.

This is what you should take with you

Line search is a fundamental component of optimization algorithms, guiding the adaptive selection of step sizes during the optimization process.
It provides adaptability, improving convergence and stability in a wide range of optimization problems.
When compared to fixed step sizes, line search offers enhanced convergence properties and adaptability.
Line search can be integrated with optimization techniques like gradient descent, Newton’s method, conjugate gradient, stochastic gradient descent, and trust region methods.
While beneficial, line search introduces additional computational overhead in the optimization process.
It is not a universal solution and may not be suitable for all optimization problems.
Understanding and implementing line search is essential for practitioners in the field of numerical optimization.