In der sich ständig weiterentwickelnden Landschaft der Datenwissenschaft und des maschinellen Lernens haben sich Techniken wie die Lasso Regression als unschätzbare Werkzeuge für die Vorhersagemodellierung und Merkmalsauswahl erwiesen. Lasso steht für Least Absolute Shrinkage and Selection Operator und ist eine Regressionsmethode, die nicht nur Ergebnisse vorhersagt, sondern auch das Rauschen durchforstet, um die einflussreichsten Variablen zu identifizieren.

Dieser Artikel führt Dich in die Feinheiten der Lasso Regression ein und beleuchtet ihre mathematischen Grundlagen, praktischen Anwendungen und die Unterschiede zu anderen Regressionsmethoden. Unabhängig davon, ob Du ein erfahrener Datenwissenschaftler bist oder gerade erst in die Welt der Regressionsanalyse eintauchst, kann das Verständnis der Lasso-Prinzipien und -Leistungen Deine Fähigkeiten zur Vorhersagemodellierung erheblich verbessern. Lass uns also die Geheimnisse der Lasso-Regression lüften und herausfinden, wie sie die datengesteuerte Entscheidungsfindung entscheidend verändern kann.

Was ist die Lasso Regression?

Die Lasso Regression, kurz für “Least Absolute Shrinkage and Selection Operator”, ist eine beliebte Regressionstechnik, die in der Datenanalyse und beim maschinellen Lernen eingesetzt wird. Es handelt sich dabei um eine Variante der linearen Regression, die eine Regularisierung einführt, um die Modellleistung und die Merkmalsauswahl zu verbessern. Das Hauptziel der Lasso Regression besteht darin, das am besten passende lineare Modell zu finden und gleichzeitig die Koeffizienten der weniger wichtigen Merkmale gegen Null zu reduzieren.

Bei der Lassoregression ist der zur Kostenfunktion der linearen Regression hinzugefügte Regularisierungsterm der absolute Wert der Koeffizienten, multipliziert mit einem Abstimmungsparameter (λ). Dieser Term bestraft große Koeffizienten und zwingt einige von ihnen dazu, genau Null zu werden. Infolgedessen führt die Lasso Regression effektiv eine Merkmalsauswahl durch, indem sie bestimmte Merkmale aus dem Modell ausschließt, was sie besonders nützlich macht, wenn es um Datensätze mit vielen potenziell irrelevanten oder redundanten Merkmalen geht.

Die Lasso Regression schafft ein Gleichgewicht zwischen einer guten Anpassung der Daten und der Vermeidung einer Überanpassung. Indem sie die Koeffizienten gegen Null schrumpfen lässt, fördert sie ein einfacheres Modell, das sich besser auf neue, ungesehene Daten verallgemeinern lässt. Diese Eigenschaft macht die Lasso Regression zu einem wertvollen Werkzeug in Situationen, in denen Interpretierbarkeit und Modellkomplexität entscheidende Faktoren sind.

Durch ihren einzigartigen Ansatz zur Regularisierung und Merkmalsauswahl bietet die Lasso Regression eine effektive Möglichkeit, Vorhersagemodelle zu erstellen und gleichzeitig Multikollinearität zu behandeln und die Auswirkungen irrelevanter Merkmale zu reduzieren. In den folgenden Abschnitten werden die Mechanismen, Vorteile und Anwendungen der Lasso Regression in verschiedenen realen Szenarien näher erläutert.

Was ist die Gleichung der Lasso Regression?

Die Lasso Regression verändert die standardmäßige lineare Regressionsgleichung, indem sie einen Regularisierungsterm hinzufügt, der das Modell dazu ermutigt, kleine Koeffizientenwerte zu haben. Die Kostenfunktion für die Lasso Regression kann wie folgt ausgedrückt werden

\(\) \[ \text{Cost}(\beta) = \text{Least Squares Loss} + \lambda \sum_{i=1}^{n} |\beta_i| \]

Hier ist eine Aufschlüsselung der Komponenten:

• Kosten(β): Die Gesamtkosten oder der Fehler im Zusammenhang mit den Vorhersagen des Modells auf der Grundlage der Koeffizienten β.
• Verlust der kleinsten Quadrate: Dies ist die traditionelle Verlustfunktion der kleinsten Quadrate, die die quadratische Differenz zwischen den vorhergesagten Werten und den tatsächlichen Zielwerten misst.
• λ (Lambda): Dies ist der Regularisierungsparameter oder Strafterm. Er steuert die Stärke der Regularisierung. Ein höheres λ führt zu einer stärkeren Regularisierung, was wiederum zu kleineren Koeffizientenwerten führt. Die Wahl von λ ist entscheidend für die Steuerung des Kompromisses zwischen Modellkomplexität und Genauigkeit.
• Summenterm: Dieser Term stellt die Summe der absoluten Werte der Koeffizientenschätzungen 𝛽i dar. Er ist die L1-Norm des Koeffizientenvektors. Das Hauptziel der Lassoregression ist die Minimierung dieser Kostenfunktion durch Anpassung der Koeffizienten 𝛽i unter Berücksichtigung des Regularisierungsterms. Das Hauptmerkmal von Lasso ist, dass es einen absoluten Wert in den Regularisierungsterm einbezieht, so dass es in der Lage ist, die Koeffizienten ganz auf Null zu schrumpfen.

Beispiel:

Lass uns die Lassoregression anhand eines einfachen Beispiels veranschaulichen. Nehmen wir an, wir möchten die Hauspreise auf der Grundlage mehrerer Merkmale wie Quadratmeterzahl, Anzahl der Schlafzimmer und Lage vorhersagen. Die Lasso-Regressionsgleichung für dieses Problem würde lauten:

\(\) \[ \text{House Price} = \beta_0 + \beta_1 \times \text{Square Footage} + \beta_2 \times \text{Number of Bedrooms} + \beta_3 \times \text{Location} + \ldots \]

In dieser Gleichung sind 𝛽0, 𝛽1 usw. die Koeffizienten, die der Lasso-Algorithmus schätzen wird. Der Regularisierungsterm, der durch λ gesteuert wird, sorgt dafür, dass einige dieser Koeffizienten genau Null werden können, wodurch bestimmte Merkmale effektiv aus dem Modell entfernt werden. Diese Fähigkeit zur Merkmalsauswahl ist ein entscheidender Vorteil der Lasso Regression, insbesondere bei Datensätzen mit vielen Merkmalen oder potenziellen Multikollinearitätsproblemen.

Was sind die Vor- und Nachteile der Lasso Regression?

Die Lasso Regression ist eine beliebte Technik im Bereich der linearen Regression, die eine Reihe von Vor- und Nachteilen mit sich bringt. In diesem Abschnitt werden wir uns mit den Besonderheiten befassen, die Lasso zu einem wertvollen Werkzeug machen und wo es möglicherweise Grenzen hat. Das Verständnis dieser Aspekte ist wichtig, um fundierte Entscheidungen bei der Anwendung der Lasso Regression auf reale Datenanalyseaufgaben treffen zu können.

Vorteile der Lasso Regression:

• Auswahl der Merkmale: Die Lasso Regression ist für ihre Fähigkeit zur Merkmalsauswahl bekannt. Sie fördert die Sparsamkeit des Modells, was bedeutet, dass die Koeffizienten irrelevanter oder redundanter Merkmale auf genau Null gesetzt werden. Dies führt zu einem einfacheren und besser interpretierbaren Modell. In einem Modell zur Vorhersage von Immobilienpreisen könnte Lasso beispielsweise automatisch erkennen, dass die Anzahl der Schlafzimmer und Bäder die wichtigsten Prädiktoren sind, während weniger relevante Merkmale außer Acht gelassen werden.
• Verhindert Überanpassung: Der Regularisierungsterm von Lasso, der durch den Parameter lambda dargestellt wird, trägt dazu bei, eine Überanpassung zu verhindern. Zu einer Überanpassung kommt es, wenn ein Modell extrem gut zu den Trainingsdaten passt, aber bei ungesehenen Daten eine schlechte Leistung erbringt. Die Regularisierung von Lasso bestraft große Koeffizientenwerte und reduziert so effektiv die Komplexität des Modells und seine Tendenz zur Anpassung an das Rauschen in den Trainingsdaten.
• Behandelt Multikollinearität: Multikollinearität entsteht, wenn die Prädiktorvariablen in einem Regressionsmodell stark korreliert sind. Dies kann bei der traditionellen Regression zu Problemen führen, aber Lasso kann damit effektiv umgehen. Dazu wird eine der korrelierten Variablen ausgewählt, während die Koeffizienten der anderen Variablen auf Null gesetzt werden. Wenn beispielsweise zwei Variablen, wie “Einkommen” und “Bildungsjahre”, stark korreliert sind, kann Lasso eine auswählen und den Koeffizienten der anderen auf Null setzen.
• Robustheit gegenüber Ausreißern: Die Lasso Regression ist relativ robust gegenüber dem Vorhandensein von Ausreißern im Datensatz. Ausreißer sind extreme Datenpunkte, die ein herkömmliches Regressionsmodell unverhältnismäßig stark beeinflussen können, was zu verzerrten Parameterschätzungen führt. Die Regularisierung von Lasso reduziert die Auswirkungen von Ausreißern und macht das Modell robuster.
• Interpretierbarkeit: Die Einfachheit, die durch die Merkmalsauswahl in Lasso erreicht wird, macht das Modell besser interpretierbar. In Fällen, in denen Sie die Vorhersagen des Modells nicht-technischen Interessengruppen erklären müssen, ist ein spärliches Modell mit weniger Prädiktoren leichter zu vermitteln und zu verstehen.

Nachteile der Lasso-Regression:

• Selektionsverzerrung: Die Merkmalsauswahl ist zwar ein Vorteil, kann aber auch zu einer Selektionsverzerrung führen. Wenn das Lasso fälschlicherweise wichtige Variablen aus dem Modell ausschließt, kann dies zu einem verzerrten Modell führen, das wesentliche Beziehungen in den Daten nicht erfasst.
• Instabil bei korrelierten Prädiktoren: Lasso kann bei stark korrelierten Prädiktoren instabil sein. Kleine Änderungen im Datensatz oder die Einbeziehung leicht unterschiedlicher Variablen können zu einer anderen Variablenauswahl führen. Diese Instabilität kann es schwierig machen, sich auf einen bestimmten Satz von ausgewählten Variablen zu verlassen.
• Wahl von Lambda: Die Effektivität von Lasso hängt von der Wahl eines geeigneten Wertes für den Regularisierungsparameter Lambda ab. Die Wahl des richtigen Lambda erfordert Techniken wie die Kreuzvalidierung, die rechenintensiv sein kann und nicht immer eine offensichtliche Wahl ermöglicht.
• Nicht für alle Datensätze ideal: Lasso ist am effektivsten, wenn es einen echten Grund für die Annahme gibt, dass einige Prädiktoren genau Nullkoeffizienten haben sollten. Bei Datensätzen, bei denen wahrscheinlich alle Merkmale relevant sind, sind andere Regressionstechniken, wie z. B. die Ridge-Regression, die die Koeffizienten gegen Null schrumpfen lässt, sie aber nicht auf Null zwingt, möglicherweise besser geeignet.
• Verlust von Informationen: Durch die Verringerung der Größe der Koeffizienten kann Lasso einige Informationen verlieren, die für die Erstellung von Vorhersagen nützlich sein könnten. In Fällen, in denen alle Prädiktoren wirklich informativ sind, kann die Tendenz von Lasso, einige Koeffizienten auf Null zu setzen, im Vergleich zu nicht regulierten Regressionsmethoden zu einem weniger genauen Modell führen.

Zusammenfassend lässt sich sagen, dass die Lasso Regression ein leistungsfähiges Werkzeug im Bereich der Regressionsanalyse ist, insbesondere wenn es um die Auswahl von Merkmalen, den Umgang mit Multikollinearität oder die Vermeidung von Überanpassungen geht. Bei der Entscheidung, ob Lasso oder eine andere Regressionsmethode am besten geeignet ist, muss man sich jedoch ihrer Grenzen bewusst sein und die Art des Datensatzes und die spezifischen Ziele der Analyse berücksichtigen.

Lasso vs. Ridge vs. Elastic Net

Im Bereich der linearen Regression zielen verschiedene Regularisierungstechniken darauf ab, die Modellleistung zu verbessern und die Herausforderungen der Multikollinearität zu bewältigen. Lasso, Ridge und Elastic Net sind drei solcher Techniken, die jeweils ihre eigenen Merkmale und Anwendungsfälle haben. Lasse uns untersuchen, wie sich diese Methoden unterscheiden und wann Du eine der anderen vorziehen kannst.

Lasso Regression:

Vorteile:

• Merkmalsauswahl: Lasso führt eine automatische Merkmalsauswahl durch, indem es die Koeffizienten von irrelevanten oder weniger wichtigen Merkmalen auf Null setzt.
• Einfachheit: Es ist einfach zu implementieren und zu interpretieren.

Nachteile:

• Instabil bei vielen Merkmalen: Lasso kann bei einer großen Anzahl von Merkmalen instabil sein und eine Teilmenge von Merkmalen zufällig auswählen.
• Nicht-eindeutige Lösungen: Bei stark korrelierten Merkmalen kann Lasso zu nicht eindeutigen Lösungen führen.

Ridge-Regression:

Vorteile:

• Stabilität: Die Ridge-Regression ist bei der Behandlung von Multikollinearität stabiler als Lasso.
• Eindeutige Lösung: Sie ergibt immer eine eindeutige Lösung, auch bei stark korrelierten Merkmalen.

Nachteile:

• Führt keine Merkmalsauswahl durch: Ridge führt keine Merkmalsselektion durch; es verkleinert die Koeffizienten gegen Null, eliminiert sie aber nicht.

Elastic Net:

Vorteile:

• Ausgewogenheit: Elastic Net kombiniert die Stärken von Lasso und Ridge. Es kann eine Merkmalsauswahl durchführen und Multikollinearität effektiv behandeln.
• Abstimmbarkeit: Die Kombination von L1- (Lasso) und L2-Regularisierung (Ridge) ermöglicht eine Feinabstimmung der Balance zwischen Merkmalsauswahl und Koeffizientenschrumpfung.

Nachteile:

• Komplexität: Elastic Net beinhaltet einen zusätzlichen Hyperparameter zur Steuerung des Gleichgewichts zwischen L1- und L2-Regularisierung, was es etwas komplexer macht als Lasso oder Ridge allein.

Wann sollte man was wählen:

• Lasso: Verwende Lasso, wenn Du vermutest, dass nur eine Teilmenge Deiner Merkmale relevant ist, und Du eine automatische Merkmalsauswahl wünscht. Es ist auch geeignet, wenn Du mit hochdimensionalen Daten arbeitest.
• Ridge: Entscheide Dich für Ridge, wenn Du Probleme mit Multikollinearität hast und eine stabilere Lösung wünscht. Ridge ist auch eine gute Wahl, wenn Du der Meinung bist, dass alle Merkmale zur Vorhersage beitragen, Du aber deren Einfluss reduzieren möchtest.
• Elastic Net: Elastic Net stellt ein Gleichgewicht zwischen Lasso und Ridge dar und ist nützlich, wenn Du gleichzeitig eine Merkmalsauswahl und eine Behandlung der Multikollinearität benötigst. Es bietet einen besser abstimmbaren Ansatz.

In der Praxis hängt die Wahl zwischen Lasso, Ridge oder Elastic Net von Deinen spezifischen Daten, dem zu lösenden Problem und den Kompromissen ab, die Du zwischen Merkmalsauswahl und Multikollinearitätsbehandlung einzugehen bereit bist. Experimente und Kreuzvalidierung sind wertvolle Werkzeuge, um herauszufinden, welche Methode für Deine spezielle Modellierungsaufgabe am besten geeignet ist.

Wie kannst Du Training und Hyperparameter-Tuning für die Lasso Regression durchführen?

Die Abstimmung der Hyperparameter ist ein wichtiger Schritt bei der Erstellung genauer und robuster Modelle für maschinelles Lernen, einschließlich der Lasso Regression. Bei der Lasso Regression ist der wichtigste abzustimmende Hyperparameter die Regularisierungsstärke, die oft als “Alpha” (α) bezeichnet wird. Dieser Parameter steuert das Ausmaß, in dem Lasso die absoluten Werte der Koeffizienten bestraft.

Hier findest Du eine Schritt-für-Schritt-Anleitung, wie Du die Hyperparameter in der Lasso-Regression abstimmen kannst:

1. Definiere einen Bereich von Alpha-Werten:

Definiere zunächst einen Bereich von Alphawerten, den Du während des Abstimmungsprozesses untersuchen möchtest. Dieser Bereich sollte von sehr kleinen Werten (nahe Null) bis zu größeren Werten reichen, die häufig auf einer logarithmischen Skala verteilt sind.

2. Teile Deine Daten auf:

Teile Deinen Datensatz in zwei Teilmengen auf: einen Trainingssatz und einen Validierungssatz. Der Trainingssatz wird verwendet, um mehrere Lasso Regressionsmodelle mit unterschiedlichen Alpha-Werten zu trainieren, während der Validierungssatz zur Bewertung ihrer Leistung eingesetzt wird.

3. Lasso-Modelle trainieren:

Iteriere durch die vordefinierten Alpha-Werte und trainiere ein separates Lasso Regressionsmodell für jeden Alpha-Wert unter Verwendung des Trainingsdatensatzes. Ziel ist es, zu beurteilen, wie sich verschiedene Alpha-Werte auf die Leistung des Modells auswirken.

4. Bewerte die Modellleistung:

Nachdem Du jedes Lasso-Modell trainiert hast, bewertest Du die Leistung des Modells auf dem Validierungsdatensatz anhand einer geeigneten Bewertungsmetrik. Übliche Metriken sind R-Quadrat, mittlerer quadratischer Fehler (MSE) oder jede andere geeignete Metrik für Dein spezifisches Problem.

5. Wähle das beste Alpha:

Wähle den Alpha-Wert, der die beste Modellleistung auf dem Validierungsset ergibt. Dieses Alpha ist dasjenige, das Du für Dein endgültiges Lasso-Regressionsmodell verwenden solltest.

6. Teste mit Holdout-Daten:

Nachdem Du den besten Alphawert ausgewählt hast, empfiehlt es sich, das ausgewählte Modell auf einem separaten Holdout-Testdatensatz zu testen, auf den es während des Trainings oder der Validierung nicht gestoßen ist. Dies ermöglicht eine abschließende Bewertung der Leistung Deines Modells.

7. Kreuzvalidierung (optional):

Für eine robustere Bewertung solltest Du eine k-fache Kreuzvalidierung anstelle einer einfachen Trainingsvalidierung verwenden. Die Kreuzvalidierung hilft sicherzustellen, dass die Leistung Deines Modells über verschiedene Datenaufteilungen hinweg stabil ist.

8. Feinabstimmung (optional):

Falls erforderlich, kannst Du andere Hyperparameter, wie z. B. die Wahl eines bestimmten Solvers oder Toleranzniveaus, je nach Deiner Softwarebibliothek und Deinen spezifischen Anforderungen weiter feinabstimmen.

Die Abstimmung der Hyperparameter ist ein iterativer Prozess, bei dem Du versuchst, das richtige Gleichgewicht zwischen Modellkomplexität (gesteuert durch Alpha) und Vorhersagegenauigkeit zu finden. Experimentiere mit verschiedenen Alphawerten, um ihre Auswirkungen auf die Leistung Deines Modells zu bewerten, und wähle denjenigen, der am besten zu Deinem spezifischen Problem und Datensatz passt.

Wie kann man die Lasso Regression in Python implementieren?

Die Lasso Regression, eine beliebte lineare Regressionstechnik mit L1-Regularisierung, kann mit Bibliotheken wie scikit-learn effektiv in Python implementiert werden. Im Folgenden werden die Schritte zur Implementierung der Lasso-Regression anhand eines Beispiels mit dem California Housing-Datensatz erläutert, einem öffentlich verfügbaren Datensatz, der häufig für Regressionsaufgaben verwendet wird.

1. Importiere die erforderlichen Bibliotheken:

Beginne mit dem Importieren der erforderlichen Bibliotheken für Deine Python-Umgebung. Du benötigst scikit-learn für die Modellierung, NumPy für numerische Operationen und möglicherweise weitere Bibliotheken für die Datenmanipulation und -visualisierung.

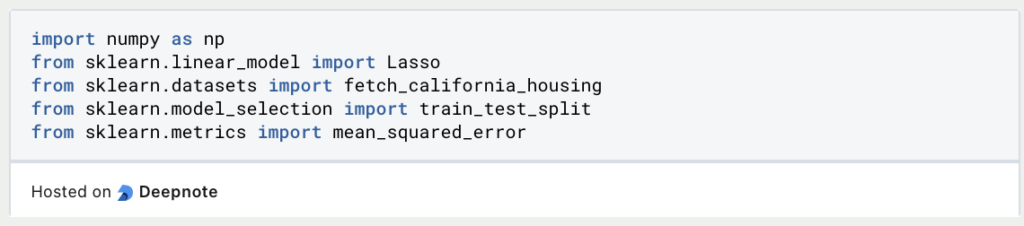
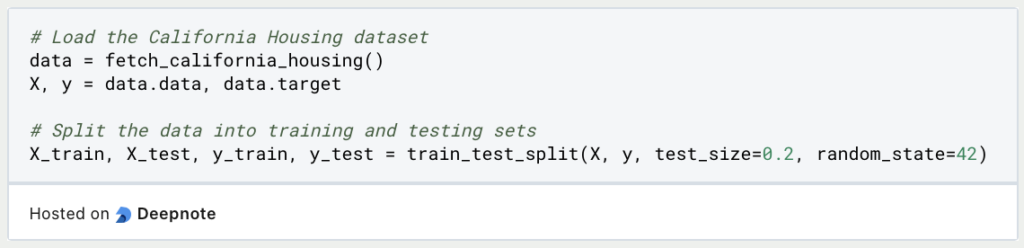
2. Lade den Datensatz und bereite ihn vor

Lade den Datensatz “California Housing”, der über das Modul “Datasets” von scikit-learn verfügbar ist. Teile die Daten in Merkmale (X) und die Zielvariable (y) auf und unterteile sie weiter in Trainings- und Testsätze.

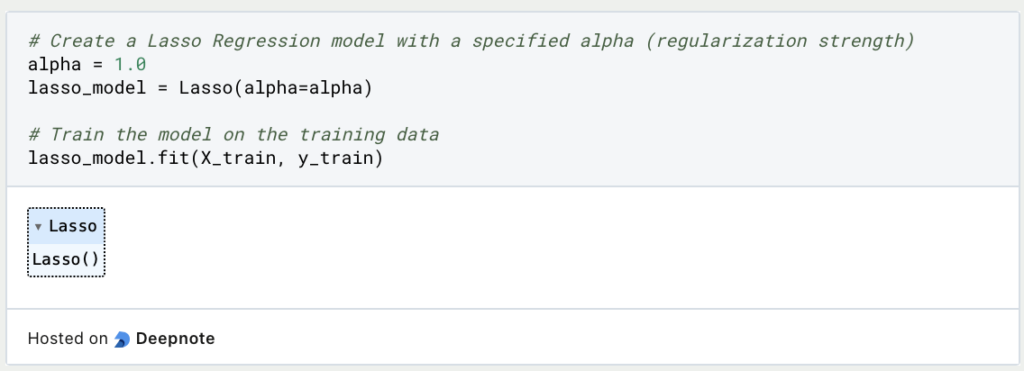
3. Erstelle und Trainiere das Lasse Regressionsmodell:

Erstelle anschließend eine Instanz des Lasso Regressionsmodells und gebe die Stärke der Regularisierung (Alpha) an. Trainiere das Modell anhand der Trainingsdaten.

4. Treffe Vorhersagen:

Verwenden Sie das trainierte Lasso Regressionsmodell, um Vorhersagen für die Testdaten zu treffen.

5. Evaluiere das Modell

Bewerte die Leistung des Lasso Regressionsmodells anhand geeigneter Bewertungsmaßstäbe. Für Regressionsaufgaben werden in der Regel Metriken wie der mittlere quadratische Fehler (MSE) oder R-Quadrat verwendet.

6. Hyperparameter Tuning (Optional):

Du kannst eine Feinabstimmung des Alpha-Hyperparameters vornehmen, indem Du mit verschiedenen Werten experimentierst und denjenigen auswählst, der zur besten Modellleistung führt. Techniken wie die Kreuzvalidierung können bei diesem Prozess helfen.

Dieses Beispiel zeigt, wie die Lasso-Regression in Python unter Verwendung der scikit-learn-Bibliothek mit dem Datensatz California Housing implementiert werden kann. Beachte, dass die Wahl des Datensatzes und der spezifischen Hyperparameter je nach Deinem speziellen Regressionsproblem variieren kann.

Wie interpretiert man die Parameter der Lasso Regression?

Die Interpretation der Parameter (Koeffizienten) in einem Lasso Regressionsmodell ist entscheidend für das Verständnis der Beziehung zwischen den unabhängigen Variablen (Merkmalen) und der abhängigen Variable (Ziel). Bei der Lasso Regression werden die Koeffizienten einer L1-Regularisierung unterzogen, was dazu führen kann, dass einige Koeffizienten genau Null sind. Diese Eigenschaft der Merkmalsauswahl macht die Interpretation relativ einfach.

1. Nicht-Null-Koeffizienten:

Bei der Lasso Regression werden einige Koeffizienten im Rahmen des Merkmalsauswahlprozesses in der Regel auf genau Null gesetzt. Dies sind die Variablen, die das Modell als irrelevant für die Vorhersage der Zielvariablen betrachtet. Wenn ein Koeffizient nicht Null ist, bedeutet dies, dass das entsprechende Merkmal eine Auswirkung auf die Zielvariable hat, die nicht Null ist.

2. Vorzeichen des Koeffizienten:

Das Vorzeichen (positiv oder negativ) eines Koeffizienten ungleich Null gibt die Richtung der Beziehung zwischen dem Merkmal und dem Ziel an. Ist der Koeffizient eines Merkmals beispielsweise positiv, so führt eine Erhöhung des Merkmalswerts zu einer Erhöhung der vorhergesagten Zielvariable, und umgekehrt bei einem negativen Koeffizienten.

3. Größe der Koeffizienten:

Die Größe der Koeffizienten spiegelt die Stärke der Beziehung zwischen den einzelnen Merkmalen und dem Ziel wider. Größere Koeffizientenwerte weisen auf einen stärkeren Einfluss auf das Ziel hin, während kleinere Werte auf einen schwächeren Einfluss hindeuten. Sie können die Größenordnungen der Koeffizienten vergleichen, um festzustellen, welche Merkmale einen größeren Einfluss haben.

4. Wichtigkeit des Merkmals:

Durch die Untersuchung der Koeffizienten, die nicht Null sind, kannst Du feststellen, welche Merkmale für die Vorhersage des Ziels am wichtigsten sind. Merkmale mit Nicht-Null-Koeffizienten tragen zur Vorhersagekraft des Modells bei. Dies kann für die Auswahl von Merkmalen und die Vereinfachung Ihres Modells von Nutzen sein.

5. Koeffizientenstabilität:

Bei der Lasso Regression kann die Stabilität der Koeffizienten mit verschiedenen Alpha-Werten (Regularisierungsstärke) variieren. Kleinere Alphawerte führen tendenziell zu stabileren und besser interpretierbaren Koeffizienten. Das Experimentieren mit Alpha-Werten und das Beobachten von Veränderungen in den Koeffizienten kann Ihnen helfen zu verstehen, wie empfindlich Ihr Modell auf verschiedene Regularisierungsstufen reagiert.

6. Fachwissen:

Die Interpretation von Koeffizienten ist zwar von entscheidender Bedeutung, aber es ist auch wichtig, statistische Erkenntnisse mit Fachwissen zu kombinieren. Wenn Du den Kontext Deiner Daten verstehst und weißt, wie die Variablen zueinander in Beziehung stehen, kannst Du wertvolle Einblicke in die praktischen Auswirkungen der Koeffizientenwerte gewinnen.

Denke daran, dass die Interpretation der Koeffizienten in der Lasso Regression im Vergleich zu anderen Regressionstechniken aufgrund der Merkmalsauswahl einfacher ist. Sie ermöglicht es Dir, sich auf die für Deine Analyse und Entscheidungsfindung wichtigsten Variablen zu konzentrieren.

Das solltest Du mitnehmen

• Die Lasso Regression ist ein wertvolles Instrument für die Auswahl von Merkmalen und hilft bei der Ermittlung der wichtigsten Variablen in einem Datensatz.
• Sie bietet Robustheit gegenüber Überanpassung, indem sie der linearen Regression einen Strafterm hinzufügt, was zu einer besseren Generalisierung führen kann.
• Die L1-Regularisierung von Lasso führt oft zu spärlichen Lösungen, bei denen viele Koeffizienten genau Null sind, was das Modell vereinfacht.
• Lasso und Ridge-Regression bieten verschiedene Arten der Regularisierung, und die Wahl zwischen ihnen hängt von dem spezifischen Problem und den gewünschten Modelleigenschaften ab.
• Die Feinabstimmung des Alpha-Parameters ist entscheidend für die Optimierung der Leistung der Lasso-Regression.
• Die Implementierung der Lasso Regression in Python, insbesondere mit Bibliotheken wie scikit-learn, ist unkompliziert und ermöglicht es Praktikern, sie auf reale Datensätze anzuwenden.
• Die Eigenschaften der Lasso-Merkmalsauswahl verbessern die Interpretierbarkeit des Modells und machen es in einigen Bereichen zu einer bevorzugten Wahl.
• Eine korrekte Datenskalierung ist bei der Lasso-Regression unerlässlich, um eine faire Regularisierung für alle Merkmale zu gewährleisten.

Andere Beiträge zum Thema Lasso Regression

Die Dokumentation für die Lasso Regression in Scikit-Learn findest Du hier.