Im Bereich der digitalen Logik und der Informatik ist XOR (Exclusive OR) ein kleiner, aber unglaublich leistungsfähiger Operator. Er spielt eine zentrale Rolle in verschiedenen Anwendungen, von der Verschlüsselung bis zu mathematischen Operationen und künstlicher Intelligenz. Dieser Artikel taucht in die Welt des XOR ein und erläutert seine grundlegenden Konzepte, seine realen Anwendungen und seine Bedeutung in Technik und Mathematik.
Was ist XOR (Exklusives ODER)?
XOR, kurz für Exclusive OR, ist eine grundlegende logische Operation, die in der digitalen Elektronik, der Mathematik, der Computerprogrammierung und verschiedenen Anwendungen verwendet wird. Es handelt sich um einen Binäroperator, der zwei Binärwerte (0 und 1) annimmt und nach bestimmten Regeln ein Ergebnis erzeugt. Die Operation wird “exklusiv” genannt, weil sie nur dann wahr (1) ist, wenn einer der Eingabewerte wahr (1) ist, aber nicht beide. So funktioniert sie:
- Eingabewerte: Die XOR-Verknüpfung benötigt zwei binäre Eingabewerte, die in der Regel als A und B bezeichnet werden, wobei jeder Wert entweder 0 oder 1 sein kann.
- Ausgabe: Die XOR-Verknüpfung ergibt 1, wenn die Anzahl der wahren (1) Eingaben ungerade ist. Mit anderen Worten, sie liefert 1, wenn die Eingaben unterschiedlich sind (eine wahr und eine falsch).
Die Wahrheitstabelle dafür sieht so aus:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
In der Wahrheitstabelle kannst Du sehen, dass der Algorithmus nur dann 1 ausgibt, wenn es eine “exklusive” wahre Eingabe gibt (entweder ist A wahr oder B wahr, aber nicht beides). Wenn beide Eingaben gleich sind (beide wahr oder beide falsch), ergibt XOR 0.
Die Vielseitigkeit von XOR und seine Rolle in verschiedenen Bereichen machen es zu einem grundlegenden Konzept in der Welt der Technik und Mathematik. Es ist ein Baustein für viele Operationen und eine Schlüsselkomponente in zahlreichen realen Anwendungen.
Was ist die Definition von XOR?
XOR oder Exklusiv-ODER ist eine grundlegende Binäroperation, die in verschiedenen Bereichen verwendet wird, insbesondere in der digitalen Elektronik und Informatik. Sie zeichnet sich durch ihren ausschließenden Charakter aus und ermöglicht es uns, festzustellen, wann sich zwei Binärwerte unterscheiden. Im Folgenden werden die Definition und die Funktionsweise von XOR sowie die Wahrheitstabelle erläutert.
XOR-Operation:
- XOR ist eine Binäroperation, die zwei Eingänge benötigt, die normalerweise als A und B dargestellt werden und jeweils entweder 0 oder 1 sein können.
- Die XOR-Operation liefert ein Ergebnis, das davon abhängt, ob die Eingänge gleich oder verschieden sind.
- Sie gibt 1 aus, wenn die Anzahl der wahren (1) Eingänge ungerade ist. Mit anderen Worten: XOR liefert 1, wenn die Eingänge sich gegenseitig ausschließen, d. h. einer wahr und der andere falsch ist.
Erläuterung:
- In der XOR-Wahrheitstabelle kann man sehen, dass XOR 1 ausgibt, wenn die Eingänge unterschiedlich sind (einer wahr und einer falsch) und 0, wenn sie gleich sind (beide wahr oder beide falsch).
- Wenn A und B beide 0 oder beide 1 sind, ergibt die XOR-Operation 0, was bedeutet, dass es keinen Unterschied zwischen den Eingängen gibt.
- Wenn A gleich 0 und B gleich 1 ist, oder wenn A gleich 1 und B gleich 0 ist, ergibt die XOR-Verknüpfung 1, was bedeutet, dass sich die Eingänge tatsächlich ausschließen.
Beispiele für XOR in Aktion:
- Binäre Addition ohne Übertrag: XOR wird häufig bei der binären Addition ohne Übertrag verwendet. Bei der Addition zweier Binärzahlen wird XOR auf jedes Paar entsprechender Bits angewendet, um die Summe zu erhalten, während der Übertrag separat berechnet wird. Zum Beispiel:
- 1 XOR 0 = 1 (ohne Übertrag)
- 1 XOR 1 = 0 (mit Übertrag)
- Toggle-Operation: XOR wird verwendet, um ein Bit oder einen Wert umzuschalten. Durch wiederholte XOR-Verknüpfung desselben Wertes mit einem anderen Bit wird zwischen 0 und 1 gewechselt, was in der Computerprogrammierung für Aufgaben wie das Umschalten einer Flagge oder eines Zustands nützlich ist.
Das Verständnis der XOR-Operation ist in verschiedenen Bereichen von zentraler Bedeutung, von der digitalen Logik und der Binärarithmetik bis hin zur Computerprogrammierung und Kryptografie. Die XOR-Verknüpfung bietet eine einzigartige Möglichkeit, die Ungleichheit zwischen Binärwerten festzustellen, was sie zu einer vielseitigen und unverzichtbaren Operation in der Welt der Technik und Mathematik macht.
Wie ist XOR in Logikgattern definiert?
XOR-Gatter, kurz für Exklusiv-ODER-Gatter, sind grundlegende Komponenten in digitalen Logikschaltungen. Diese Gatter können mit Hilfe von grundlegenden Logikgattern (UND, ODER, NICHT) konstruiert werden und finden in verschiedenen Aspekten digitaler Schaltungen für eine breite Palette von Zwecken Anwendung. Im Folgenden wird erläutert, wie XOR-Gatter aus grundlegenden Logikgattern aufgebaut sind und welche vielseitige Rolle sie in digitalen Schaltungen spielen.
Aufbau von XOR-Gattern:
XOR-Gatter können aus einer Kombination grundlegender Logikgatter aufgebaut werden, vor allem aus UND-, ODER- und NICHT-Gattern. Der gängigste Ansatz besteht darin, zwei ODER-Gatter, zwei UND-Gatter und ein NICHT-Gatter zu verwenden, um ein XOR-Gatter zu erstellen. Hier ist eine schrittweise Erklärung:
ODER-Gatter: Zunächst wird die XOR-Operation mit Hilfe von zwei ODER-Gattern auf die beiden Eingangswerte (A und B) angewendet. Dazu wird die Umkehrung (NOT) eines der Eingangswerte genommen und als zweiter Eingang in das ODER-Gatter eingespeist.
UND-Gatter: Die Ausgänge der beiden ODER-Gatter werden dann mit zwei separaten UND-Gattern verbunden. Diese UND-Gatter verarbeiten die Ergebnisse weiter.
Endgültiger XOR-Ausgang: Der endgültige XOR-Ausgang ergibt sich aus der Verbindung der Ausgänge der beiden UND-Gatter. Durch diese Anordnung wird sichergestellt, dass das XOR-Gatter die gewünschten Ergebnisse auf der Grundlage der Exklusiv-Operation liefert.
Verwendung von XOR-Gattern in digitalen Schaltungen:
XOR-Gatter sind vielseitige Komponenten in digitalen Schaltungen, die ein breites Spektrum von Anwendungen bieten:
- Binäre Addition: XOR-Gatter werden häufig in der Binärarithmetik verwendet. Sie sind für die Addition von Binärzahlen verantwortlich, ohne zum nächsten Bit überzugehen, was in der digitalen Datenverarbeitung unerlässlich ist.
- Datenverschlüsselung: Die Gatter spielen eine entscheidende Rolle bei Verschlüsselungsalgorithmen, wie z. B. der XOR-Chiffre. Sie sind von grundlegender Bedeutung für die Sicherung von Daten und Kommunikation, indem sie bitweise Operationen auf die Daten anwenden.
- Paritätsprüfung: Sie werden auch zur Berechnung von Paritätsbits für die Fehlererkennung und -korrektur bei der Datenübertragung verwendet. Dadurch wird die Integrität und Genauigkeit der übertragenen Daten sichergestellt.
- Arithmetische Schaltungen: Diese Gatter sind von zentraler Bedeutung für die Konstruktion von arithmetischen Schaltungen, einschließlich Subtraktoren und Komparatoren.
- Multiplexer und Demultiplexer: XOR-Gatter werden in Multiplexern und Demultiplexern eingesetzt, um Datensignale weiterzuleiten und zu dekodieren.
- Elektronische Bauteile: Sie werden in elektronische Komponenten und integrierte Schaltungen integriert und bieten eine grundlegende logische Operation für komplexe digitale Systeme.
- Rechnen und Verarbeitung: XOR-Gatter sind integraler Bestandteil von Computerprozessoren und Speichereinheiten, die Aufgaben wie Adressdekodierung und Datenmanipulation übernehmen.
XOR-Gatter sind unverzichtbare Werkzeuge in der digitalen Elektronik, mit denen sich binäre Daten auf verschiedene Weise manipulieren und verarbeiten lassen. Ihre Konstruktion aus einfachen Logikgattern und ihre umfangreichen Anwendungen unterstreichen ihre Bedeutung als Schlüsselkomponenten in der modernen Digitaltechnik.
Was sind die Anwendungen von XOR?
XOR, oder Exklusiv-ODER, ist eine Binäroperation mit einer breiten Palette von Anwendungen in verschiedenen Bereichen, von der digitalen Elektronik und Informatik bis hin zur Mathematik und Kryptografie. Die einzigartigen Eigenschaften dieser vielseitigen Operation machen sie zu einer unverzichtbaren Komponente in einer Vielzahl von praktischen Anwendungen. Hier werden wir einige der wichtigsten Anwendungen von XOR in diesen verschiedenen Bereichen untersuchen.
- Digitale Logik und Elektronik:
- XOR-Gatter sind grundlegende Bausteine in digitalen Schaltungen, die verschiedene Operationen ermöglichen. Sie werden bei der binären Addition ohne Übertrag verwendet, die für arithmetische und logische Einheiten in Computern entscheidend ist.
- XOR-Gatter sind Teil von Flip-Flops und Speicherzellen, die für die Speicherung und Verarbeitung von Daten in Computersystemen entscheidend sind.
- Computerprogrammierung:
- XOR ist in der Computerprogrammierung weit verbreitet. Es wird bei bitweisen Operationen verwendet, wo es hilft, Bits umzuschalten, Werte zu vertauschen und Daten zu manipulieren.
- XOR ist ein grundlegendes Werkzeug für die Lösung von Programmierproblemen und ermöglicht es Entwicklern, Code zu optimieren und effiziente Algorithmen zu erstellen.
- Kryptographie:
- XOR ist von zentraler Bedeutung für viele kryptografische Algorithmen, einschließlich der XOR-Chiffre. Durch die bitweise XOR-Verknüpfung von Klartext und einem geheimen Schlüssel können Daten sicher ver- und entschlüsselt werden.
- Kryptografische Hash-Funktionen wie HMAC verwenden häufig XOR-Operationen, um die Sicherheit und Integrität von Daten zu verbessern.
- Fehlererkennung und -korrektur:
- XOR wird zur Berechnung von Paritätsbits für die Fehlererkennung bei der Datenübertragung verwendet. Durch Hinzufügen von Paritätsbits zu den Daten können Fehler erkannt und korrigiert werden, wodurch die Datenintegrität gewährleistet wird.
- RAID-Systeme (Redundant Array of Independent Disks) verwenden XOR-Operationen, um Fehlertoleranz und Datenwiederherstellungsmöglichkeiten zu bieten.
- Mathematik:
- XOR ist ein integraler Bestandteil der modularen Arithmetik und wird in verschiedenen mathematischen Problemen und Rätseln verwendet.
- In der Graphentheorie spielt XOR eine Rolle bei der Lösung von Problemen im Zusammenhang mit Konnektivität und Netzwerkfluss.
- Maschinelles Lernen und künstliche Intelligenz:
- XOR ist ein grundlegendes Konzept in neuronalen Netzen. Es hilft neuronalen Netzen, komplexe Beziehungen zwischen Eingaben und Ausgaben zu modellieren, wodurch sie Aufgaben wie Klassifizierung, Regression und Mustererkennung durchführen können.
- Deep Learning, ein Teilbereich der künstlichen Intelligenz, stützt sich auf XOR-ähnliche Operationen, um komplexe Modelle für komplexe Aufgaben zu erstellen.
- Datenintegrität und -überprüfung:
- XOR wird verwendet, um die Integrität von Datenübertragungen zu überprüfen, insbesondere bei Kommunikationsprotokollen und der Datenspeicherung.
- Prüfsummen, zyklische Redundanzprüfungen (CRCs) und Prüfsummenalgorithmen verwenden XOR, um Fehler in Daten zu erkennen.
- Puzzles und Spiele:
- XOR-Verknüpfungen werden häufig in Rätseln und Spielen verwendet und stellen eine Herausforderung für Problemlösungsbegeisterte und Programmierer dar.
Das Verständnis von XOR und seinen Anwendungen ist für Fachleute aus den Bereichen Technik, Mathematik und Kryptographie unerlässlich. Es ist nach wie vor ein grundlegendes Konzept in digitalen Systemen, das die Entwicklung sicherer Kommunikation, effizienter Algorithmen und fortschrittlicher Datenmanipulationstechniken ermöglicht. Die Vielseitigkeit von XOR gewährleistet seine fortwährende Relevanz in einer sich ständig weiterentwickelnden technologischen Landschaft.
Wie wird XOR in der Informatik verwendet?
In der dynamischen Welt der Informatik spielt XOR (Exklusiv-ODER) eine zentrale Rolle in einer Vielzahl von Anwendungen, die von einfachen bitweisen Operationen bis hin zum Entwurf komplizierter Algorithmen reichen. Es ist ein vielseitiger Operator, der für seine einzigartigen Eigenschaften bekannt ist, und sein Einfluss durchdringt verschiedene Facetten der Informatik.
Bitweise Operationen:
Dieses Gatter ist in den bitweisen Operationen zu Hause, wo es sich durch die Manipulation einzelner Bits in binären Darstellungen auszeichnet. Es dient als Eckpfeiler, um bestimmte Bits effizient umzuschalten, zu setzen oder zu löschen.
Datenverschlüsselung und Hashing:
XOR ist ein Dreh- und Angelpunkt bei der Datenverschlüsselung und beim Hashing. Bei kryptografischen Operationen wird Klartext mit geheimen Schlüsseln verschmolzen, um Chiffretext zu erzeugen, der Vertraulichkeit und Datenintegrität gewährleistet. Eine Vielzahl von Verschlüsselungs-Chiffren stützt sich auf XOR, um ihre Robustheit zu gewährleisten.
Datenmanipulation und Algorithmen:
Der Einfluss von XOR ist in Computeralgorithmen allgegenwärtig. Sei es beim Suchen, Sortieren oder bei der Datentransformation, XOR wird zum Dreh- und Angelpunkt für eine rationalisierte Datenmanipulation und einen bitweisen Vergleich.
Fehlererkennung und -korrektur:
In Computernetzwerken und Datenspeichersystemen übernimmt XOR die Rolle der Paritätsbitberechnung. Paritätsbits sind die Wächter vor Fehlern, sie ermöglichen die Erkennung und Korrektur von Anomalien und stellen sicher, dass die Daten intakt bleiben.
Hardware und Mikrocontroller-Programmierung:
XOR kommt in der Hardware- und Mikrocontroller-Programmierung zum Einsatz. Es steuert die Steuerung von Eingangs- und Ausgangspins, ermöglicht das Aktivieren und Deaktivieren spezifischer Hardwarekomponenten und koordiniert die Interaktion von Geräten auf niedriger Ebene.
Datenkomprimierung:
Dieses Gate eignet sich für einige Datenkomprimierungstechniken, bei denen es die Darstellung und Speicherung von Daten optimiert. Auf diese Weise wird die Größe der komprimierten Daten verringert, während die Genauigkeit der Dekompression erhalten bleibt.
Pseudozufallszahlengenerierung:
XOR übernimmt die Rolle von Pseudozufallszahlengeneratoren (PRNGs), die für Anwendungen wie Simulationen, Kryptographie und Spiele gefragt sind. Durch XOR-Verknüpfung früherer Zustände mit sorgfältig ausgewählten Konstanten werden pseudozufällige Sequenzen erzeugt.
Musterabgleich und Kryptoanalyse:
Dieses Gatter erweist sich als unverzichtbares Werkzeug für den Musterabgleich und die Kryptoanalyse. Ob es darum geht, wiederkehrende Sequenzen zu erkennen oder Schwachstellen aufzudecken, XOR hilft beim Aufspüren von Mustern und Anomalien.
XOR-Gatter in digitalen Schaltungen:
XOR-Gatter, die mühsam aus einfachen Logikgattern aufgebaut wurden, bilden die Grundlage für die Architektur von Computern. Sie sind die Grundlage für arithmetische Schaltungen, dienen als Datenspeicherelemente und spielen eine zentrale Rolle bei der digitalen Signalverarbeitung.
Entwurf von Algorithmen:
XOR-Operationen sind das Fundament, auf dem Algorithmen entwickelt werden. Sie bilden den Grundstein für die Entwicklung von Algorithmen, die binäre Daten effizient verarbeiten und vergleichen.
Für Informatiker und Softwareentwickler ist ein solides Verständnis von XOR nicht nur von Vorteil, sondern unerlässlich. Die Fähigkeit von XOR, die Speichernutzung zu optimieren, die Datensicherheit zu gewährleisten und die Leistung von Algorithmen zu verbessern, macht es zu einem unschätzbaren Vorteil in der sich ständig weiterentwickelnden Welt der Computerwissenschaft. Ob es darum geht, Daten vor neugierigen Blicken zu schützen, algorithmische Operationen zu beschleunigen oder die Grundlagen der Computerarchitektur zu sichern, XOR steht an vorderster Front und treibt Innovationen und Problemlösungen voran.
Wie wird XOR beim maschinellen Lernen und bei der KI eingesetzt?
In der sich ständig weiterentwickelnden Landschaft des maschinellen Lernens und der künstlichen Intelligenz nimmt die XOR-Verknüpfung (Exclusive OR) eine grundlegende und unersetzliche Rolle ein. Seine einzigartigen Eigenschaften und Fähigkeiten haben weitreichende Auswirkungen, prägen die Entwicklung komplexer Modelle und ermöglichen eine Vielzahl von Anwendungen für maschinelles Lernen.
Neuronale Netze und Deep Learning:
XOR ist ein grundlegendes Konzept in neuronalen Netzen und bildet die Basis, auf der diese Netze aufgebaut sind. Beim Deep Learning, einem Teilbereich des maschinellen Lernens, sind XOR-Verknüpfungen entscheidend für die Erstellung komplexer Modelle mit mehreren Schichten miteinander verbundener Neuronen. Diese Architektur ermöglicht die Modellierung komplizierter Muster und die Lösung komplexer Aufgaben.
XOR-Gatter in neuronalen Netzen:
In den Architekturen neuronaler Netze sind XOR-Gatter, die aus grundlegenden Logikgattern aufgebaut sind, wesentliche Bestandteile. Diese Gatter spielen eine wichtige Rolle bei der Konstruktion hochentwickelter Modelle, die in der Lage sind, komplexe Probleme durch schichtweise Berechnungen zu lösen.
Lösen komplexer Aufgaben und Mustererkennung:
XOR-ähnliche Operationen spielen eine zentrale Rolle bei der Bewältigung komplexer Aufgaben, die das Verstehen nichtlinearer Beziehungen zwischen Eingabemerkmalen und gewünschten Ausgaben erfordern. Modelle des maschinellen Lernens nutzen diese Operationen, um sich in Bereichen wie Klassifizierung, Regression, Mustererkennung und komplizierten Problemlösungen auszuzeichnen.
In der Welt des maschinellen Lernens ist das Verständnis der Bedeutung von XOR für Forscher und Praktiker unerlässlich. Die Fähigkeit von XOR, komplizierte Datenbeziehungen zu modellieren, die Lerneffizienz zu verbessern und die Lösung komplexer Aufgaben zu ermöglichen, zementiert seinen Status als entscheidende Komponente bei der Entwicklung fortschrittlicher KI-Systeme. Ob es nun tiefe neuronale Netze antreibt, die Mustererkennung erleichtert oder Lernprozesse optimiert, XOR bleibt an der Spitze der Revolution des maschinellen Lernens und der künstlichen Intelligenz.
Wie kann man XOR in Python implementieren?
Die Implementierung von XOR (Exklusiv-ODER) in Python ist einfach, da Python einen eingebauten XOR-Operator (^) für ganze Zahlen bietet. XOR kann auf zwei Ganzzahlen oder binäre Darstellungen von Ganzzahlen angewendet werden. Im Folgenden wird beschrieben, wie man XOR in Python implementiert:
Verwendung des ^-Operators:
Du kannst den ^-Operator direkt verwenden, um XOR-Operationen mit ganzen Zahlen durchzuführen. Hier ist ein einfaches Beispiel:
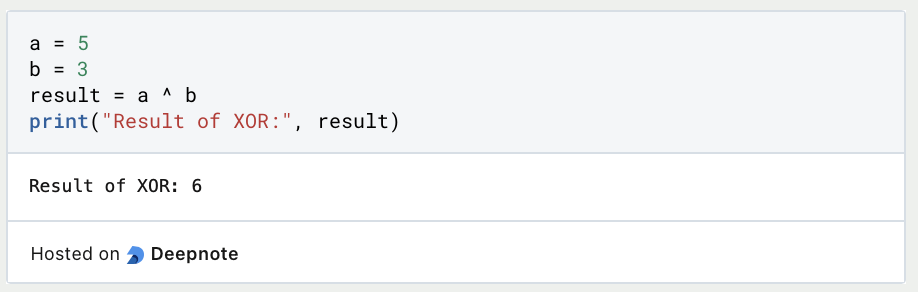
In diesem Beispiel wird die XOR-Verknüpfung zwischen den ganzen Zahlen a und b durchgeführt, und das Ergebnis wird in der Ergebnisvariablen gespeichert.
XOR auf binäre Zeichenketten:
Du kannst XOR auch implementieren, indem Du Ganzzahlen in binäre Zeichenketten umwandelst und XOR auf jedes Bit anwendest. Hier ist ein Beispiel für XOR auf binäre Strings:

In diesem Beispiel nimmt die Funktion xor_binary_strings zwei binäre Zeichenketten und wendet XOR bitweise an. Sie behandelt auch Fälle, in denen die binären Zeichenketten unterschiedliche Längen haben, indem sie die kürzere Zeichenkette mit Nullen auffüllt.
Die XOR-Operation ist ein grundlegendes Konzept in der Informatik und der Programmierung, und Python macht die Arbeit mit ihr einfach. Ganz gleich, ob Du mit ganzen Zahlen oder binären Darstellungen arbeitest, Python bietet die Werkzeuge, um XOR effizient zu implementieren.
Das solltest Du mitnehmen
- XOR (Exklusives ODER) ist eine grundlegende Binäroperation mit einzigartigen Eigenschaften und vielseitigen Anwendungen.
- In der Informatik ist XOR ein Eckpfeiler der bitweisen Operationen, der Entwicklung von Algorithmen und neuronalen Netzen und ermöglicht komplexe Problemlösungen.
- XOR wird bei der Datenverschlüsselung und der Fehlererkennung eingesetzt, um die Sicherheit und Integrität von Daten zu verbessern.
- XOR bietet zwar viele Vorteile, hat aber auch seine Tücken, wie z. B. seine Empfindlichkeit gegenüber Datenungleichgewichten und seine begrenzte Anwendbarkeit bei einigen Aufgaben.
- Um die Stärken und Grenzen von XOR zu verstehen, ist es wichtig, seine Leistungsfähigkeit in verschiedenen Bereichen effektiv zu nutzen.
- Es spielt eine wichtige Rolle in der digitalen Welt und treibt Innovationen und Problemlösungen in der Informatik, dem maschinellen Lernen und der Kryptografie voran.
Python-Tutorial: Bedingte Anweisungen und If/Else Blöcke
Lernen Sie, wie man bedingte Anweisungen in Python verwendet. Verstehen Sie if-else und verschachtelte if- und elif-Anweisungen.
Wie kannst Du die Ausnahmebehandlung in Python umsetzen?
Die Kunst der Ausnahmebehandlung in Python: Best Practices, Tipps und die wichtigsten Unterschiede zwischen Python 2 und Python 3.
Was sind Python Module?
Erforschen Sie Python Module: Verstehen Sie ihre Rolle, verbessern Sie die Funktionalität und rationalisieren Sie die Programmierung.
Was sind Python Vergleichsoperatoren?
Beherrschen Sie die Python Vergleichsoperatoren für präzise Logik und Entscheidungsfindung beim Programmieren in Python.
Was sind Python Inputs und Outputs?
Python Inputs und Outputs beherrschen: Erforschen Sie Eingaben, Ausgaben und den Umgang mit Dateien in der Python-Programmierung.
Wie kannst Du mit Python Excel / CSV Dateien bearbeiten?
In diesem Artikel werden Möglichkeiten aufgezeigt, um mit Python Excel- und CSV-Dateien öffnen, bearbeiten und schreiben zu können.
Andere Beiträge zum Thema XOR
Hier findest Du die Dokumentation, wie man das in Python macht.

Niklas Lang
Seit 2020 bin ich als Machine Learning Engineer und Softwareentwickler tätig und beschäftige mich leidenschaftlich mit der Welt der Daten, Algorithmen und Softwareentwicklung. Neben meiner Arbeit in der Praxis unterrichte ich an mehreren deutschen Hochschulen, darunter die IU International University of Applied Sciences und die Duale Hochschule Baden-Württemberg, in den Bereichen Data Science, Mathematik und Business Analytics.
Mein Ziel ist es, komplexe Themen wie Statistik und maschinelles Lernen so aufzubereiten, dass sie nicht nur verständlich, sondern auch spannend und greifbar werden. Dabei kombiniere ich praktische Erfahrungen aus der Industrie mit fundierten theoretischen Grundlagen, um meine Studierenden bestmöglich auf die Herausforderungen der Datenwelt vorzubereiten.





