Bayes’sche Netze, oder englisch Bayesian Networks, sind eine Art von probabilistischen, grafischen Modellen, die auf der Wahrscheinlichkeitstheorie und insbesondere auf dem Bayes Theorem beruhen. Das Ziel ist es dabei, die komplexen Abhängigkeiten zwischen einzelnen Komponenten kompakt und verständlich zu modellieren und darzustellen. Bayes‘sche Netze werden in unterschiedlichsten Anwendungen, wie beispielsweise medizinischen Diagnose oder bei Risikobewertungen, eingesetzt. 

In diesem Artikel werden wir uns im Detail mit Bayesian Networks beschäftigen und deren Aufbau genauer verstehen. Dazu schauen wir uns nicht nur das Bayes Theorem an, sondern stellen uns auch die Frage, wie man ein solches Netzwerk erstellt und daraus Schlussfolgerungen ziehen kann. Nachdem wir ein Bayesian Network in Python gebaut haben, vergleichen wir diese Methode mit anderen, ähnlichen Methoden. 

Was sind Bayes’sche Netze?

Bayes’sche Netze, oder englisch Bayesian Networks, sind graphische Modelle, welche die probabilistischen Abhängigkeiten zwischen Variablen in einem Datensatz darstellen. Dafür werden Knoten und Kanten verwendet, wobei Knoten die einzelnen Variablen repräsentieren und die Kanten die (bedingten) Wahrscheinlichkeiten zwischen diesen Variablen beschreiben. Das Ziel ist es hierbei die komplexen Abhängigkeiten und Dynamiken zwischen den Knoten darzustellen und leichter verständlich zu machen. 

Solche Modelle sind in den unterschiedlichsten Bereichen äußerst wertvoll, vor allem dann, wenn sie bei komplexen Entscheidungen unterstützen, bei denen keine absolute Sicherheit vorherrscht und man deshalb auf die Wahrscheinlichkeiten zurückgreift. Folgende Anwendungen nutzen Bayesian Networks: 

• Machine Learning: Bayes’sche Netze können im Bereich des Machine Learnings für die Datenklassifizierung, die Merkmalsextraktion oder zur Musterkennung verwendet werden. Dadurch können sie helfen, Modelle zu trainieren, welche auf unsicheren oder unvollständigen Daten beruhen. 
• Entscheidungsfindung: In diesem Bereich sind Bayesian Networks von Vorteil, da sie die Beziehungen zwischen Faktoren quantifizieren und außerdem kausale Zusammenhänge übersichtlich darstellen können. 
• Datenanalyse: In der Datenanalyse unterstützen Bayesian Networks dabei, Muster in großen Datenmengen zu erkennen und außerdem Vorhersagen zu treffen, welche von zufälligen Variationen beeinflusst werden. 

Der Vorteil von Bayes’schen Netzen besteht darin, dass sie es ermöglichen komplexe Abhängigkeiten darzustellen, ohne starre Annahmen zu treffen. 

Was besagt das Bayes Theorem?

Um den Aufbau eines Bayesian Networks im Detail verstehen zu können, ist es wichtig die mathematischen und statistischen Grundlagen zu verstehen. Deshalb machen wir uns in diesem Abschnitt mit der Wahrscheinlichkeitstheorie, den bedingten Wahrscheinlichkeiten und abschließend mit dem Bayes Theorem vertraut. 

In der Wahrscheinlichkeitstheorie befassen wir uns mit der Quantifizierung von Unsicherheiten. Es wird also versucht Ereignisse zu beschreiben, deren Ausgang nicht sicher ist. Die Wahrscheinlichkeit gibt dann den Grad der Unsicherheit an mit dem das Ereignis eintritt.

Nehmen wir an, wir wollen für ein Wohngebiet quantifizieren, ob das Ereignis „Einbruch“ eintritt oder nicht. In einem Zeitraum von 10 Jahren kann es passieren, dass in dem Wohngebiet nie eingebrochen wird, es kann aber auch genauso gut sein, dass ein Einbruch stattfindet. Diese Unsicherheit, ob das Ereignis „Einbruch“ eintritt, können wir mit einer Wahrscheinlichkeit abbilden. Eine Einbruchswahrscheinlichkeit von 10% besagt beispielsweise, dass es in einem Zeitraum von zehn Jahren mit einer Wahrscheinlichkeit von 10% zu einem Einbruch kommt. Zu 90% hingegen tritt das Ereignis „Einbruch“ nicht ein. 

Eine besondere Form der Wahrscheinlichkeit ist hierbei die sogenannte konditionale Wahrscheinlichkeit, welche einfach gesagt ausdrückt, mit welcher Wahrscheinlichkeit ein Ereignis eintritt, unter der Bedingung, dass ein anderes Ereignis bereits mit Sicherheit eingetreten ist. 

Angenommen wir haben zwei Variablen A und B, dann repräsentiert die bedingte Wahrscheinlichkeit P(A|B), die Wahrscheinlichkeit, dass A eintritt, wenn B bereits mit Sicherheit eingetreten ist. Ein einfaches Beispiel ist eine Alarmanlage und die dazugehörige bedingte Wahrscheinlichkeit P(Alarm|Einbruch) oder in anderen Worten: „Wie hoch ist die Wahrscheinlichkeit, dass die Alarmanlage auslöst, wenn mit Sicherheit ein Einbruch stattgefunden hat?“

Das Bayes Theorem wiederum eröffnet eine Möglichkeit, wie wir unsere Annahmen von Wahrscheinlichkeiten im Laufe der Zeit verändern können, wenn neue Informationen oder Daten verfügbar sind. Allgemein gesprochen ergibt sich die bedingte Wahrscheinlichkeit zwischen den Ereignissen A und B mithilfe der folgenden Formel: 

\(\)\[P(A|B)\ =\ \frac{P(B|A)\ \cdot P(A)}{P(B)} \]

Hierbei sind: 

• \(P(A|B)\) ist die bedingte Wahrscheinlichkeit, dass das Ereignis A eintritt, wenn das Ereignis B bereits mit Sicherheit eingetreten ist. 
• \(P(B|A)\) ist die bedingte Wahrscheinlichkeit, dass Ereignis B eintritt, wenn Ereignis A mit Sicherheit eingetreten ist. 
• \(P(A)\) ist die Wahrscheinlichkeit, dass das Ereignis A eintritt. 
• \(P(B)\) ist die Wahrscheinlichkeit, dass das Ereignis B eintritt. 

Das Bayes Theorem wird neben der Aktualisierung von Wahrscheinlichkeiten auch häufig genutzt, wenn die bedingte Wahrscheinlichkeit \(P(A|B)\) unbekannt ist, jedoch die bedingte Wahrscheinlichkeit \(P(B|A)\) deutlich einfacher zu bestimmen ist. 

Kommen wir zurück zu unserem Beispiel mit der Alarmanlage und den Einbrüchen. Angenommen wir haben die folgenden Ereignisse: 

• Ereignis \(A\): Die Alarmanlage geht los.
• Ereignis \(B\): Ein Einbruch hat stattgefunden. 

Mithilfe des Bayes Theorem möchten wir nun die bedingte Wahrscheinlichkeit errechnen, dass auch wirklich ein Einbruch stattgefunden hat \((B)\), wenn der Alarm losgeht \((A)\), also \(P(B|A)\). Um das Bayes Theorem anwenden zu können benötigen wir die folgenden Wahrscheinlichkeiten:

• \(P(B)\) die Wahrscheinlichkeit, dass ein Einbruch stattfindet. Wir nehmen an, dass das Risiko eines Einbruchs sehr gering ist, also \(P(B) = 0,01\), bzw. die Einbruchswahrscheinlichkeit liegt bei 1%.
• \(P(A|B)\) beschreibt die Wahrscheinlichkeit, dass die Alarmanlage losgeht, wenn ein Einbruch stattfindet. Diese hängt von vielen Faktoren ab, wie beispielsweise, ob alle Fenster von der Anlage erfasst werden oder wie häufig es zu Stromausfällen kommt währenddessen zwar eingebrochen werden kann, aber die Alarmanlage nicht auslösen kann. Für unser Beispiel gehen wir von einer Wahrscheinlichkeit von 90%, also 0,9, aus, sodass Einbrüche nahezu immer von der Alarmanlage erfasst werden.
• \(P(A)\) beschreibt die Wahrscheinlichkeit, dass die Alarmanlage losgeht, unabhängig davon, ob ein Einbruch stattgefunden hat oder nicht. Diese Wahrscheinlichkeit setzt sich aus zwei Fällen zusammen: 
  • Erster Fall: Die Alarmanlage geht los, weil eingebrochen wurde. Diese Wahrscheinlichkeit ergibt sich aus der Wahrscheinlichkeit, dass eingebrochen wurde \(P(B)\), multipliziert mit der Wahrscheinlichkeit, dass die Alarmanlage aufgrund des Einbruchs auch angeschlagen hat, also \(P(A|B)\). 
  • Zweiter Fall: Die Alarmanlage geht los, obwohl kein Einbruch stattgefunden hat. Diese Wahrscheinlichkeit ergibt sich daraus, dass kein Einbruch stattgefunden hat, also \(1 – P(B)\) multipliziert mit der Wahrscheinlichkeit, dass die Alarmanlage einen Fehlalarm hatte, also \(P(A|\neg B)\). Wir nehmen an, dass der Hersteller eine Fehlalarmquote von 5%, also 0,05, besitzt. Somit ergibt sich für die Wahrscheinlichkeit \(P(A)\), dass ein Alarm ausgelöst wird: 

\(\)\[P(A)\ =\ P(A|B)\ \cdot (B)\ +\ P(A|\neg B)\ \cdot (\neg B)\ =\ (0,9\ \cdot 0,01)\ +\ (0,05\ \cdot 0,99)\ =\ 0,0585\]

Mithilfe von diesen Werten können wir nun die bedingte Wahrscheinlichkeit \(P(B|A)\) mithilfe des Bayes Theorems ausrechnen: 

\(\)\[P(B|A)\ =\ \frac{P(A|B)\ \cdot P(B)}{P(A)}\ =\ \frac{0,9\ \cdot 0,01}{0,0585}\ =\ 0,1538\]

Somit liegt die Wahrscheinlichkeit, dass wirklich ein Einbruch vorliegt, wenn die Alarmanlage losgeht, bei etwa 15 % liegt. In diesem Fall hilft also das Bayes Theorem die Wahrscheinlichkeit eines Einbruchs realistisch einzuschätzen, indem es berücksichtigt, wie zuverlässig die Alarmanlage ist und wie häufig Fehlalarme vorkommen. 

Wie ist ein Bayesian Network strukturiert?

Die Struktur von Bayesian Networks basiert auf den zwei grundlegenden Konzepten von Knoten und Kanten, mit denen komplexe Beziehungen zwischen verschiedenen Zufallsvariablen aufgebaut und veranschaulicht werden können. In diesem Abschnitt stellen wir die Konzepte dar und veranschaulichen sie an einem einfachen Beispiel. 

Knoten

Die Knoten in einem Bayesian Network repräsentieren Zufallsvariablen, die verschiedene Zustände annehmen können. Jeder Knoten besitzt die Möglichkeit, entweder diskrete Werte, wie „Ja“ oder „Nein“, oder kontinuierliche Werte, wie zum Beispiel Temperaturangaben, anzunehmen. In unserem Beispiel betrachten wir drei verschiedene Knoten: 

• Wetter: Dieser Knoten ist diskret und besitzt verschiedene Zustände, wie zum Beispiel „sonnig“, „regnerisch“ oder „verschneit“. 
• Verkehr: Dieser Knoten beschreibt die Verkehrslage auf dem Arbeitsweg eines Individuums, welcher die Zustände „Stau“ oder „kein Stau“ annehmen kann. 
• Zur Arbeit gehen: Der letzte Knoten entscheidet darüber, ob das Individuum zur Arbeit fährt oder im Homeoffice arbeitet. Somit kann er die Zustände „Ja“ oder „Nein“ annehmen. 

Um die Abhängigkeiten dieser Knoten zu beschreiben und sie in eine Verbindung zu stellen, benötigen wir als nächstes die Kanten, welche die kausalen Beziehungen aufbauen. 

Kanten

Die Kanten, welche zwischen den Knoten verlaufen, stellen die Beziehungen zwischen den Zufallsvariablen dar. Hierbei ist wichtig, dass diese Beziehungen gerichtet sind und somit von einem Knoten zum anderen Verlaufen, wobei die Richtung eine Bedeutung hat. Eine gerichtete Kante vom Knoten „Wetter“ zum Knoten „Verkehr“ sagt beispielsweise aus, dass das Wetter einen Einfluss auf den Verkehr hat, da bei Schneefall die Autos langsamer fahren und deshalb das Risiko für Staus steigt. 

Die gerichteten Kanten sind wichtig für die Struktur des Netzwerks, da sie die logischen Abhängigkeiten definieren und somit einen entscheidenden Einfluss auf die Wirkweise des Netzwerks haben. 

Grafische Darstellung

Die Darstellung des Bayesian Networks erfolgt mithilfe eines sogenannten gerichteten, azyklischen Graphen (DAG), der sich dadurch auszeichnet, dass jede Kante eine klare Richtung besitzt und von einem Knoten zum anderen zeigt, nicht aber in beide Richtungen. Außerdem gibt es keine zyklischen Abhängigkeiten zwischen den Knoten. 

Diese Darstellung hilft jedoch bei der statistischen Analyse erstmal nicht wirklich, da sich zwar die Beziehungen erkennen lässt, aber noch keine konkreten Werte und Vorhersagen abgeleitet werden können. 

Wahrscheinlichkeiten

Damit man mit dem Bayesian Network auch konkrete Vorhersagen treffen kann und die Abhängigkeiten quantifizierbar sind, müssen wir für das oben definierte Netzwerk noch die Wahrscheinlichkeiten hinzufügen. 

Hierbei gibt es zwei Arten von Wahrscheinlichkeiten, die unterschieden werden müssen. Die Prior-Wahrscheinlichkeit wird für alle „Eltern-Knoten“ definiert, also die Knoten, welche nur ausgehende Kanten haben und keine eingehenden. Diese Knoten sind komplett unabhängig von den anderen Knoten. In unserem Beispiel ist das Wetter ein solcher Eltern-Knoten. 

Alle Knoten, welche von anderen Knoten abhängig sind, benötigen bedingte Wahrscheinlichkeiten, da definiert werden muss, wie sich dieser Knoten abhängig vom Zustand des Elternknoten verhält. In unserem Beispiel sind der „Verkehr“ und „Zur Arbeit gehen“ solche abhängigen Knoten. 

1. Prior-Wahrscheinlichkeiten

Für alle Eltern-Knoten werden die sogenannten Prior-Wahrscheinlichkeiten festgelegt, welche die Ausgangszustände der Zufallsvariablen darstellen, ohne den Einfluss von anderen Knoten. In unserem Fall betrifft das nur den Knoten „Wetter“, welcher beispielsweise die folgenden Wahrscheinlichkeiten besitzen könnte: 

• \(P(W = sonnig) = 0,6\)
• \(P(W = regnerisch) = 0,3\)
• \(P(W = verschneit) = 0,1\)

Diese Wahrscheinlichkeiten können durch eine statistische Analyse gefunden werden, zum Beispiel indem über ein Jahr hinweg das Wetter beobachtet wird. Die Wahrscheinlichkeit für den Zustand „sonnig“ ergibt sich dann dadurch, dass alle sonnigen Tage gezählt werden und durch die Anzahl der untersuchten Tage, also 365, geteilt werden. Wichtig ist hierbei, dass sich die Wahrscheinlichkeiten der Zustände auf eins summieren, sodass sichergestellt ist, dass einer der Zustände auch wirklich eintreten werden. 

2. Bedingte Wahrscheinlichkeiten

Für die restlichen Knoten, welche von anderen Knoten abhängen, also Eltern besitzen, müssen bedingte Wahrscheinlichkeiten aufgestellt werden, da die Erreichung eines Zustands von dem Zustand des Elternknotens abhängt. Für den Verkehr beispielsweise ergibt sich die folgende Tabelle, welche die verschiedenen Zustände des Wetters mit einbezieht, da der Verkehr vom Wetter abhängt. Die erste Zeile sagt dann aus, dass es bei sonnigem Wetter in 10% der Fälle zu Staus kommt. Entsprechend in 90% der Fälle kommt es bei Sonne zu keinem Stau. 

Wetter	P(V = Stau)	P(V = Kein Stau)
sonnig	0,1	0,9
regnerisch	0,5	0,5
verschneit	0,8	0,2

Die Wahrscheinlichkeiten für die Zustände „Zur Arbeit gehen“ sind etwas komplexer, da diese Variable von zwei Knoten, nämlich „Verkehr“ und „Wetter“ abhängt, weshalb mehr Zeilen benötigt werden. 

Wetter	Verkehr	P(A = Ja)	P(A = Nein)
Sonnig	Stau	0,6	0,4
Sonnig	Kein Stau	0,9	0,1
Regnerisch	Stau	0,4	0,6
Regnerisch	Kein Stau	0,7	0,3
Schnee	Stau	0,2	0,8
Schnee	Kein Stau	0,5	0,5

Die erste Zeile sagt dann aus, dass bei sonnigem Wetter und Stau ein Mitarbeiter mit einer Wahrscheinlichkeit von 60% ins Büro kommt. Genauso kann es auch so interpretiert werden, dass bei den gegebenen Umständen etwa 60% der Belegschaft im Büro erscheinen. 

Nachdem wir nun den allgemeinen Aufbau des Bayesian Netzwerks verstanden haben, stellt sich jedoch noch die entscheidende Frage, wie man zu den Abhängigkeiten und den errechneten Wahrscheinlichkeiten kommen kann. Dabei gehen wir auch der Frage auf die Spur, woher das Neztwerk seinen Namen hat. 

Wie erstellt man ein Bayes’sches Netz und berechnet die Wahrscheinlichkeiten?

Um aus einem Datensatz ein Bayesian Network aufbauen zu können, benötigen wir zwei Schritte. Zum einen müssen wir die Kanten zwischen den Knoten erkennen und aufbauen und zum anderen müssen die Wahrscheinlichkeiten für die einzelnen Ereignisse und die bedingten Wahrscheinlichkeiten errechnet werden. 

Parametrisches Lernen

Das Parametrische Lernen umfasst den Prozess, bei dem aus einem gegebenen Datensatz die Parameter des Bayes’schen Netzes, also die Wahrscheinlichkeitswerte der einzelnen Knoten berechnet werden. Diese Parameter umfassen sowohl die Wahrscheinlichkeiten der einzelnen Knoten als auch die Abhängigkeiten zwischen den Knoten. Für das parametrische Lernen können zum Beispiel die folgenden Methoden eingesetzt werden: 

1. Maximum Likelihood Schätzung (MLE): Bei diesem Ansatz werden die Wahrscheinlichkeiten so gewählt, dass sie die beobachteten Daten am wahrscheinlichsten erklären. Dabei bildet die Wahrscheinlichkeit die relative Häufigkeit der Ereignisse ab, wodurch die Wahrscheinlichkeit des Auftretens der tatsächlich beobachteten Daten maximiert wird. Mithilfe von diesem Ansatz würden wir beispielsweise eine Wahrscheinlichkeit für das Wetter „sonnig“ von 70% schätzen, wenn es an 70% der beobachteten Tage sonnig war. 
2. Bayessche Schätzung: Wenn der verfügbare Datensatz klein oder unvollständig ist, kann auch die Bayessche Schätzung verwendet werden. Diese bindet, im Gegensatz zu MLE, auch die sogenannte a-priori Annahme, also vorheriges Wissen, in die Schätzung mit ein. Dieses wird dann nur noch durch die neuen, beobachteten Daten aktualisiert.

Beispiel zur Bayesschen Schätzung

Angenommen wir wollen die Wahrscheinlichkeiten für die Wetterereignisse abschätzen und haben dafür zwei verschiedene Datenquellen, welche wir in die Schätzung mit einfließen lassen wollen: 

1. Prior-Wissen: Vom Deutschen Wetterdienst erfahren wir, dass für Gesamtdeutschland gesehen die Wahrscheinlichkeit für regnerisches Wetter bei 0,3 liegt. Diese Zahl wurde durch das Sammeln von Wetterdaten über Jahre hinweg gebildet. 
2. Neue Daten: Um ein Bayes’sches Netzwerk aufbauen zu können, haben wir in den letzten sieben Tagen das Wetter an unserem Standort beobachtet und festgestellt, dass es an vier von sieben Tagen geregnet hat. 

Mithilfe von diesen beiden Quellen wollen wir unter Verwendung der Bayesschen Schätzung die Wahrscheinlichkeit für einen regnerischen Tag berechnen und beide Quellen verwenden. 

Anhand der Bayes’schen Formel müssen wir dazu die folgende Gleichung lösen: 

\(\) \[P\left(Regen\middle| D\right)=\frac{P\left(D\middle| Regen\right)\cdot P\left(Regen\right)}{P\left(D\right)} \]

Hierbei sind: 

• \(P(D|Regen)\): Die Wahrscheinlichkeit für Regen aus dem neu erstellten Datensatz, bei dem es in sieben Tagen insgesamt an vier Tagen regnerisch war, also 4/7 = 0,57.
• \(P(Regen)\) ist unsere a-priori Wahrscheinlichkeit für regnerische Daten, die wir aus unserem Vorwissen beziehen. In unserem Fall ist dies also 0,3.
• \(P(D)\) bezeichnet die Gesamtwahrscheinlichkeit der Daten, also wie wahrscheinlich es ist, die Daten zu beobachten, unabhängig davon, wie das Wetter wirklich ist. Sie ist ein wichtiger Teil der Berechnung, da sie für eine Normierung sorgt und somit sicherstellt, dass die Werte später richtig skaliert sind. Wenn wir davon ausgehen, dass nur die Zustände „Regen“ und „kein Regen“ beobachtet werden können, liegt die Gesamtwahrscheinlichkeit \(P(D) = 0,5\).

Durch Einsetzen der konkreten Werte errechnen wir eine Posteriorwahrscheinlichkeit von 0,342. Das bedeutet, dass sich die Wahrscheinlichkeit für Regen durch unser neues Wissen aus den sieben Tagen Beobachtungen leicht erhöht hat. 

\(\)\[P\left(Regen\middle| D\right)=\frac{P\left(D\middle| Regen\right)\cdot P\left(Regen\right)}{P\left(D\right)}\ =\ \frac{0,57\cdot 0,3}{0,5}\ =\ 0,342\]

Strukturelles Lernen

Nachdem wir nun die einzelnen Wahrscheinlichkeiten berechnen und updaten können, müssen wir noch herausfinden, wie wir aus dem Datensatz die Kanten zwischen den Knoten und deren Richtung ableiten. Das strukturelle Lernen beschäftigt sich genau mit dieser Frage und ergibt, welche Knoten miteinander verbunden werden und in welche Richtung die Abhängigkeiten zeigen sollen. 

Dafür werden vor allem die folgenden beiden Ansätze genutzt: 

1. Score-basierte Methoden: Bei diesen Methoden werden verschiedene mögliche Netzwerkstrukturen, die sich aus den Daten ergeben, berechnet und anhand eines bestimmten Bewertungsmaßes verglichen. Dafür können beispielsweise das Bayessche Informationskriterum (BIC) oder das Akaike Informationskriterium verwendet werden. Anschließend wird die Netzwerkstruktur mit dem höchsten Score verwendet. 
2. Constraint-basierte Methoden: Diese Vorgehensweise beruht auf statistischen Tests, welche zwischen den unterschiedlichen Variablen durchgeführt werden, um Abhängigkeiten oder Unabhängigkeiten zwischen den Knoten zu erkennen. Ein bekannter Algorithmus in diesem Bereich ist der PC-Algorithmus, welcher paarweise Unabhängigkeitstests durchführt und basierend auf den Ergebnissen eine Kante zwischen den Knoten erstellt oder nicht. 

Wie kann man ein Bayesian Network in Python umsetzen?

Bayesian Networks können in Python mithilfe von unterschiedlichen Modulen erstellt werden. In unserem Beispiel nutzen wir pgmpy, welches die Möglichkeit bietet, die Struktur des Netzes und die Wahrscheinlichkeiten zu definieren. Anschließend kann man es dann nutzen, um Entscheidungen zu treffen.

Neben pgmpy importieren wir auch Pandas, um darin die bedingten Wahrscheinlichkeiten abzulegen und an das Modell zu übergeben. Anschließend setzen wir das Modell mit den unterschiedlichen Knoten auf. Jedes der Python Tuples gibt dabei eine Kante an, die zwischen zwei Knoten verläuft. Der erstgenannte Knoten ist dabei der Startpunkt der Kante und der zweitgenannte Knoten der Endpunkt.

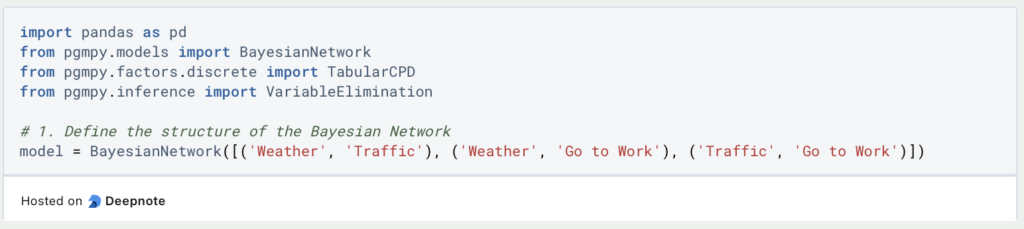
Nachdem die Netzwerkstruktur festgelegt wurde, können wir nun die Wahrscheinlichkeiten hinterlegen. Wichtig ist hierbei, dass immer die Anzahl der Variablen hinterlegt wird, also wie viel Wahrscheinlichkeiten vorhanden sind. Außerdem werden die Eltern-Knoten angegeben, wenn vorhanden. 

Dieses Modell kann nun für Schlossfolgerungen eingesetzt werden und es kann beispielsweise die Wahrscheinlichkeit berechnet werden, dass ein Mitarbeiter zur Arbeit geht, wenn es regnet und einen Stau gibt. 

Was sind die Vor- und Nachteile von Bayes’schen Netzen?

Die Bayesian Networks sind ein mächtiges Tool, um Abhängigkeiten und Wahrscheinlichkeiten in Datensätzen darzustellen und auch die Wahrscheinlichkeiten mithilfe von neuem Wissen zu aktualisieren. Deshalb werden sie in vielen Anwendungen genutzt. In diesem Abschnitt beschäftigen wir uns mit den Vor- und Nachteilen, die diese Methode bietet. 

Vorteile: 

• Flexibilität: Bayesian Networks zeichnen sich dadurch aus, dass sie für eine Vielzahl von Anwendungen und deren Abhängigkeiten genutzt werden können. Sie sind in der Lage lineare und nichtlineare Abhängigkeiten darzustellen und können leicht an verschiedene Kontexte angepasst werden. 
• Handhabung unvollständiger Daten: Auch wenn Datensätze nicht vollständig sind, bieten Bayesian Networks durch ihre probabilistische Natur die Möglichkeit fundierte Entscheidungen zu treffen, indem fehlende Werte geschätzt und die bestmöglichen Wahrscheinlichkeiten berechnet werden. 
• Transparente Entscheidungsfindung: Durch die Veranschaulichung des Netzwerks mithilfe von Knoten und Kanten ist die Entscheidungsfindung transparent und nachvollziehbar. Gerade in Anwendungen wie der Medizin oder der Rechtswissenschaft spielen diese Faktoren eine erhebliche Rolle. 

Nachteile: 

• Rechenaufwand: Bei Datensätzen mit vielen Variablen und einem daraus resultierenden großen Bayesian Network ist der Rechenaufwand immens groß und die Berechnung von Entscheidungen kann sehr lange dauern. 
• Probleme beim strukturellen Lernen: Die Erkennung der richtigen Netzwerkstruktur ist oft nicht eindeutig und deren Berechnung ist auch sehr komplex. Wenn viele Knoten vorhanden sind, nimmt die Anzahl der möglichen Netzwerkstrukturen stark zu. Außerdem ist es häufig schwierig statistisch signifikante Abhängigkeiten zwischen den Variablen zu finden. 
• Umgang mit Unsicherheiten: Zwar sind Bayesian Networks gut darin, Unsicherheiten zu modellieren und abzubilden, jedoch können sie immens an Zuverlässigkeit verlieren, wenn der Datensatz viel Rauschen enthält. 

Bayesian Networks können ein sehr leistungsfähiges Werkzeug sein bei der Entscheidungsfindung, jedoch sind sie auch gleichzeitig sehr komplex. Um das volle Potenzial ausschöpfen zu können, muss deshalb der zugrundeliegende Datensatz und die statistischen Methoden genau verstanden werden. 

Das sollest Du mitnehmen

• Bayesian Networks sind eine Art von probabilistischen, grafischen Modellen zur Veranschaulichung von Abhängigkeiten, welche mit Unsicherheiten arbeiten. 
• Sie erhalten ihren Namen von der Nutzung des Bayes Theorems, welches dabei hilft, die Wahrscheinlichkeiten zu aktualisieren. 
• Bei der Erstellung von Bayes’schen Netzen wird sowohl das parametrische Lernen, zur Abschätzung der Wahrscheinlichkeiten, als auch das strukturelle Lernen, zum Aufbau der Netzwerkstruktur, verwendet. 
• In Python kann beispielsweise das Modul pgmpy verwendet werden, um ein Bayesian Network aufzubauen und auch Schlussfolgerungen zu errechnen. 
• Die Vorteile von Bayesian Networks liegen in deren Flexibilität und deren Transparenz wie sie zu Entscheidungen kommen. 

Andere Beiträge zum Thema Bayesian Networks

Es gibt verschiedene Python-Bibliotheken, die für Bayes’sche Netze verwendet werden können. Die Dokumentation von pgmpy findest Du hier.