Der Tensor ist eine mathematische Funktion aus der linearen Algebra, die eine Auswahl von Vektoren auf einen Zahlenwert abbildet. Das Konzept stammt ursprünglich aus der Physik und wurde anschließend auch in der Mathematik verwendet. Das wohl prominenteste Beispiel, welches das Konzept der Tensoren nutzt, ist die allgemeine Relativitätstheorie.

Im Bereich des Machine Learnings werden Tensoren als Repräsentationen für viele Anwendungen genutzt, wie beispielsweise Bilder oder Videos. Sie bilden die Basis für das Machine Learning Framework TensorFlow, das seinen Namen auch daher bezieht.

Was sind der Rang und die Achse?

Wenn man Tensoren genauer beschreiben will, benötigt man den sogenannten Rang und die Dimension. Über diese lässt sich die Größe des Objektes festlegen. Dazu starten wir mit einer Matrix, deren Rang wir herausfinden wollen. Dazu bilden wir ein einfaches Numpy Array, das eine Matrix mit drei Zeilen und drei Spalten darstellt.

Der Rang eines Tensors gibt nun Auskunft darüber, wie viele Indizes man benötigt, um auf eine einzige Zahl in dem Element zu referenzieren. Es wird dabei auch oft von der Anzahl der Dimensionen gesprochen.

Im Fall einer Matrix bedeutet das, dass sie den Rang 2 (die Matrix ist zweidimensional) besitzt, da wir zwei Indizes benötigen, um eine spezifische Zahl auszugeben. Angenommen wir wollen aus dem Objekt “Matrix” die Zahl 5 in der ersten Zeile und zweiten Spalte ändern, dann benötigen wir zwei Schritte um dort hinzukommen.

Als erstes muss auf die erste Zeile mit dem Index 0 referenziert werden:

In dem Array, das wir dann erhalten, können wir auf das zweite Element mit dem Index 1 auswählen (Merke: Bei Numpy beginnt die Zählung bei 0!):

Matrizen haben also den Rang 2 (sind zweidimensional), da zwei Indizes benötigt werden, um eine Zahl zu erhalten. Jedoch gibt es viele verschiedene Größen von Matrizen, beispielsweise mit drei Zeilen und vier Spalten oder mit fünf Zeilen und zwei Spalten.

Um verschiedene Matrizen unterscheiden und genau definieren zu können, nutzen wir die sogenannten Achsen und deren Länge. Die Achse eines Tensors sind die Werte in einer spezifischen Dimension. Für unser Beispiel “Matrix” ist das Numpy Array mit dem ersten Index eine Achse in der ersten Dimension.

Die Länge der Achse wiederum sagt aus, wie viele valide Indizes es entlang der Achse gibt. In unserem Fall ist die Länge drei, da auf der ersten Achse es ingesamt drei Indizes gibt (= die Matrix hat drei Zeilen). Der folgende Aufruf führt zu einem Fehler, da es den vierten Index nicht gibt:

Was ist die Größe eines Tensors?

Die Größe eines Tensors gibt für jede Dimension die Länge der Achsen an. Das bedeutet, dass wir die Größe unseres Objektes “matrix” wie folgt angeben können:

Wir bekommen verschiedene Informationen von TensorFlow zurückgespielt, die sich relativ einfach interpretieren lassen. Der Tensor hat die “Shape” 2, also den Rang 2 bzw. zwei Dimensionen. Das hatten wir bereits erwartet, da wir wissen, dass eine Matrix ein 2-Dimensionaler Tensor ist. Der “dtype” beschreibt, welche Datentypen abgespeichert sind, in unserem Fall Ganzzahlen (Integers). Als letztes bekommen wir die Größe des Tensors mitgeteilt mit “([3,3])”, da es in jeder der zwei Dimensionen insgesamt drei verschiedene Indizes gibt. Dieses Ergebnis hatten wir bereits erwartet, da es eine Matrix mit drei Zeilen und drei Spalten ist.

Welche Arten von Tensoren gibt es?

Tensoren sind der Überbegriff von Vektoren und Matrizen und umfassen im Machine Learning Bereich mehrdimensionale Arrays. Je nachdem, welche Dimensionalität das Array besitzt, unterscheidet man verschiedene Arten:

Skalar

Der Skalar, also eine einzelne Zahl, ist ein 0-dimensionaler Tensor. Es wird kein einziger Index benötigt, um auf eine Zahl zu referenzieren. Der Skalar hat also keine Achsen und somit auch den Rang 0.

Vektor

Der Vektor ist ein 1-dimensionaler Tensor und hat den Rang 1. Je nachdem wie viele Elemente der Vektor besitzt, ändert sich die Länge der Achsen entsprechend.

Matrix

Wie wir bereits ausführlich beschrieben haben, ist die Matrix ein 2-dimensionaler Tensor.

Tensor

Ab drei oder mehr Dimensionen spricht man tatsächlich auch von Tensoren. Ein Tensor mit drei Dimensionen kann man sich als eine Ansammlung von Matrizen vorstellen.

Tensoren sind also die Verallgemeinerung aus den Objekten, welche Bereits aus der Linearen Algebra bekannt sind. In der Programmierung werden sie vor allem deshalb genutzt, weil sie die Möglichkeit bieten mehrdimensionale Datenstrukturen abzubilden.

Welche Rechenoperationen können mit ihnen gemacht werden?

Die zugelassenen Rechenoperationen sind sehr ähnlich zu denen von Matrizen, unterscheiden sich jedoch möglicherweise in der Benamung:

• Addition: Wenn zwei Objekte diesselben Dimensionen haben können sie einfach addiert werden, indem sie elementweise addiert werden und daraus ein neues Objekt mit derselben Dimensionalität entsteht.
• Substraktion: Wenn zwei Objekte diesselben Dimensionen haben können sie einfach substrahiert werden, indem sie elementweise substrahiert werden und daraus ein neues Objekt mit derselben Dimensionalität entsteht.
• Hadamard Product: Dieses spezielle Produkt entsteht, indem die Objekte elementweise miteinander multipliziert werden. Der spezielle Name kommt daher, dass es noch die “normale” Art der Multiplikation gibt, die sich an der Matrizenmultiplikation orientiert.
• Division: Wenn zwei Objekte diesselben Dimensionen haben können sie einfach dividiert werden, indem sie elementweise dividiert werden und daraus ein neues Objekt mit derselben Dimensionalität entsteht.

Welche Funktion haben sie im Machine Learning?

Um ein Machine Learning Modell trainieren zu können, werden viele Daten benötigt. Jedoch sind die Daten, wie wir sie aus der echten Welt kennen, nicht in der mathematischen Form, in der sie das Modell nutzen kann. Deshalb müssen wir beispielsweise Bilder, Videos oder Text erst in eine mehrdimensionale Datenstruktur überführen, sodass sie mathematisch interpretierbar sind.

Zugleich können Neuronale Netzwerke durch ihre Struktur eine Vielzahl von Dimensionen aufnehmen und ausgeben, die weit über herkömmliche Vektoren und Matrizen hinausgehen. Deshalb wurde mit der Verbreitung von Neural Networks auch die Nutzung von Tensoren immer häufiger.

Die folgenden Anwendungen nutzen diese Objekte in Machine Learning, um die Modellperformance zu erhöhen:

• Collaborative Filtering: Dieses Modell wird beispielsweise im E-Commerce eingesetzt, um Kunden auf einer Website möglichst passende Produkte vorzuschlagen, abhängig von deren bisherigen Kaufverhalten. Zum Training wurde klassischerweise eine Matrix genutzt, in der die bisherigen Kunden als Zeilen und die Produkte als Spalten dargestellt wurden. Wenn der Kunde in der ersten Zeile das Produkt in der zweiten Spalte bereits gekauft hat, stand an dieser Stelle eine 1 und wenn nicht eine 0. Obwohl dieser Aufbau bereits gute Ergebnisse liefern konnte, wurden diese noch weiter verbessert, indem die Matrix um Dimensionen ergänzt wurde, die dann beispielsweise auch den Kundenkontext mit einbeziehen konnte.
• Computer Vision: Bilder und Videos lassen sich nicht als eine reine Matrix darstellen. Sie enthalten nicht nur eine Vielzahl von Pixeln, sondern entstehen dadurch, dass verschiedene Farben übereinander gelegt werden und dadurch das Bild entsteht. Bei einfachen Bildern im sogenannten RGB-Format werden die Farben rot, grün und blau übereinandergelegt.

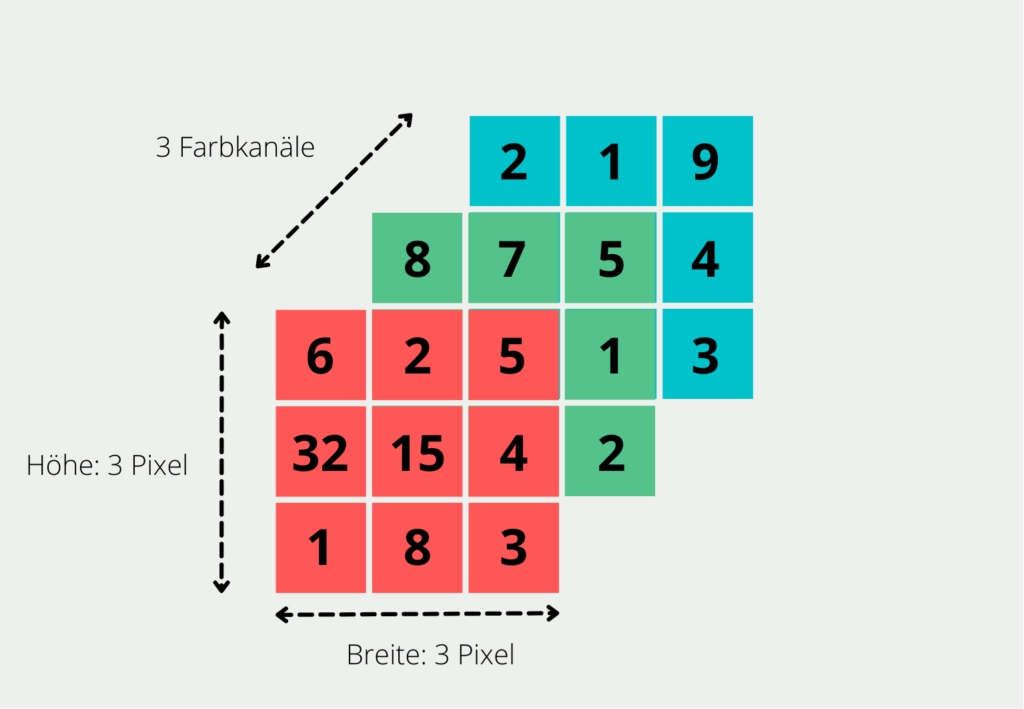
Welche Probleme ergeben sich bei der Tensoranalyse?

Tensoren sind mehrdimensionale Arrays, die in verschiedensten Bereichen, wie beispielsweise der Physik oder dem maschinellen Lernen, Anwendung finden. Sie bieten eine umfassende Möglichkeit, um komplexe Daten numerisch darzustellen. Jedoch ergibt sich bei ihrer Analyse und Darstellung die folgenden Herausforderungen, die es zu beachten gilt:

• Hohe Dimensionalität: Tensoren sind in der Zahl der Dimensionen nicht beschränkt. Bereits ab vier Dimensionen wird es schwierig diese Informationen verständlich zu visualisieren. Außerdem wird mit steigender Dimensionalität auch die Analyse schwieriger.
• Spärliche Daten: Je nach Anwendungen können einzelne Dimensionen der Tensoren sogenannte spärliche Daten enthalten. Diese treten auf, wenn die meisten Einträge in dieser Dimension null sind. Spärliche Daten erschweren die Verwendung von Techniken aus der linearen Algebra und sollten möglichst verhindert werden.
• Nicht-Eindeutigkeit: Tensoren können auf verschiedene Weisen dargestellt werden, die zwar mathematisch gleichwertig sind, aber nicht direkt identisch aussehen. Dies kann die Interpretation deutlich erschweren.
• Rechnerische Komplexität: Die Arbeit mit und Analyse von Tensoren ist rechnerisch sehr komplex und erfordert je nach Dimensionalität auch gesonderte Hardware. Dedizierte Grafikkarten eignen sich beispielsweise für die Arbeit mit großen Tensoren, jedoch sind sie nicht immer standardmäßig verbaut und es kann teuer sein diese nachzuordern.
• Vorverarbeitung der Daten: In den seltensten Fällen liegen Datensätze bereits in Tensorform vor. Deshalb müssen in der Vorverarbeitung Funktionen geschaffen werden, die die Daten umwandeln. Diese Funktionen können schnell komplex und rechenintensiv werden.
• Auswertung: Ergebnisse in Tensorform lassen sich nur schwierig interpretieren, insbesondere dann, wenn es sich um komplexe und mehrdimensionale Daten handelt.

Obwohl die Arbeit mit Tensoren komplex und rechenintensiv ist, macht die Tensoranalyse Fotschritte und die Ergebnisse bei der Analyse von multidimensionalen Daten werden immer besser. Auch in Zukunft werden weitere Entwicklungen folgen, die die Arbeit vereinfachen und zusätzliche Fortschritte im Bereich des Machine Learnings bedeuten werden.

Das solltest Du mitnehmen

• Tensoren sind mathematische Objekte aus der linearen Algebra und dienen dazu mehrdimensionale Objekte abbilden zu können.
• Mit ihnen können dieselben Rechenoperationen durchgeführt werden, die man beispielsweise von Vektoren oder Matrizen schon kennt.
• Im Machine Learning werden sie beispielsweise eingesetzt, um bessere Recommendations zu erzielen oder Bilder und Videos in Datenstrukturen abzubilden.
• Es können sich jedoch Probleme bei der Auswertung ergeben, da man oft mit einer hohen Dimensionalität und spärlichen Daten zu kämpfen hat.

Vielen Dank an Deepnote für das Sponsoring dieses Artikels! Deepnote bietet mir die Möglichkeit, Python-Code einfach und schnell auf dieser Website einzubetten und auch die zugehörigen Notebooks in der Cloud zu hosten.

Andere Beiträge zum Thema Tensor

• Ausführliche Einführung von TensorFlow