The tensor is a mathematical function from linear algebra that maps a selection of vectors to a numerical value. The concept originated in physics and was subsequently used in mathematics. Probably the most prominent example that uses the concept of tensors is general relativity.

In the field of machine learning, tensors are used as representations for many applications, such as images or videos. They form the basis for TensorFlow’s machine learning framework, which also takes its name from this.

What are the Rank and Axis?

If you want to describe tensors more precisely, you need the so-called rank and the dimension. These can determine the size of the object. For this, we start with a matrix whose rank we want to find out. For this purpose, we form a simple Numpy array, which represents a matrix with three rows and three columns.

The rank of a tensor now provides information about how many indices are needed to reference a single number in the element. It is also often referred to as the number of dimensions.

In the case of a matrix, this means that it has rank 2 (the matrix is two-dimensional) because we need two indices to output a specific number. Suppose we want to change from the object “Matrix” to the number 5 in the first row and second column, then we need two steps to get there.

First, the first line with index 0 must be referenced:

In the array that we get, we can select the second element with the index 1 (note: with Numpy, the count starts at 0!):

So matrices have rank 2 (are two-dimensional) because two indices are needed to get one number. However, there are many different sizes of matrices, for example with three rows and four columns or with five rows and two columns.

In order to distinguish different matrices and define them precisely, we use the so-called axes and their length. The axis of a tensor is the values in a specific dimension. For our example, “matrix” the Numpy array with the first index is an axis in the first dimension.

The length of the axis in turn tells how many valid indices there are along the axis. In our case the length is three because on the first axis there are three indices in total (= the matrix has three rows). The following call leads to an error because the fourth index does not exist:

What is the Size of a Tensor?

The size of a tensor gives the length of the axes for each dimension. This means that we can specify the size of our object “matrix” as follows:

We get various information fed back from TensorFlow, which can be interpreted relatively easily. The tensor has the “Shape” 2, i.e. the rank 2 or two dimensions. We already expected this, since we know that a matrix is a 2-dimensional tensor. The “dtype” describes which data types are stored, in our case integers. At last, we get the size of the tensor with “([3,3])”, because there are three different indices in each of the two dimensions. We had already expected this result since it is a matrix with three rows and three columns.

What are the different Types of Tensors?

Tensors are the umbrella term for vectors and matrices and comprise multi-dimensional arrays in the machine learning field. Depending on the dimensionality of the array, a distinction is made between different types:

Scalar

The scalar, i.e. a single number, is a 0-dimensional tensor. No single index is needed to reference a number. The scalar, therefore, has no axes and therefore also the rank 0.

Vector

The vector is a 1-dimensional tensor and has rank 1. Depending on how many elements the vector has, the length of the axes changes accordingly.

Matrix

As we have already described in detail, the matrix is a 2-dimensional tensor.

Tensor

From three or more dimensions one speaks actually also of tensors. A tensor with three dimensions can be thought of as a collection of matrices.

Tensors are the generalization from the objects, which are already known from linear algebra. They are used in programming mainly because they offer the possibility to represent multidimensional data structures.

What arithmetic Operations can be done with them?

The allowed arithmetic operations are very similar to those of matrices, but may differ in naming:

• Addition: If two objects have the same dimensions, they can be simply added by adding them element by element, and a new object with the same dimensionality is created.
• Subtraction: If two objects have the same dimensions, they can be easily subtracted by subtracting them element by element, resulting in a new object with the same dimensionality.
• Hadamard Product: This special product is created by multiplying the objects element by element. The special name comes from the fact that there is still the “normal” way of multiplication, which is based on matrix multiplication.
• Division: If two objects have the same dimensions, they can be divided simply by dividing them element by element, and a new object with the same dimensionality is created.

What is their Function in Machine Learning?

In order to train a machine learning model, a lot of data is needed. However, the data as we know it from the real world is not in the mathematical form in which the model can use it. Therefore, we must first convert images, videos, or text, for example, into a multidimensional data structure so that they can be interpreted mathematically.

At the same time, due to their structure, neural networks can accommodate and output a variety of dimensions that go far beyond conventional vectors and matrices. Therefore, with the proliferation of neural networks, the use of tensors has also become more common.

The following applications use these objects in machine learning to increase model performance:

• Collaborative Filtering: This model is used in e-commerce, for example, to suggest the most suitable products possible to customers on a website, depending on their previous purchasing behavior. For training, a matrix was classically used in which the previous customers were displayed as rows and the products as columns. If the customer in the first row had already purchased the product in the second column, a 1 was displayed at this point, and if not, a 0. Although this setup was already able to deliver good results, these were further improved by adding dimensions to the matrix, which could then also include the customer context, for example.
• Computer Vision: Images and videos cannot be represented as a pure matrix. They not only contain a large number of pixels but are created by superimposing different colors on top of each other, thus creating the image. In simple images in the so-called RGB format, the colors red, green, and blue are superimposed.

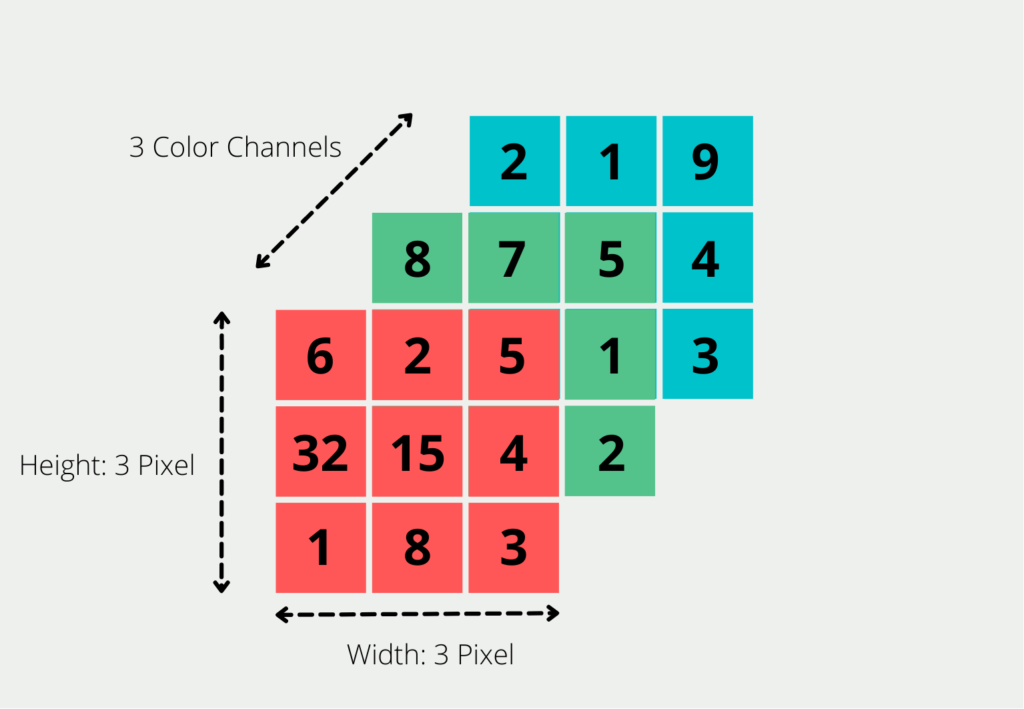
What problems arise in tensor analysis?

Tensors are multidimensional arrays that are used in a wide variety of areas, such as physics or machine learning. They offer a comprehensive way of representing complex data numerically. However, there are the following challenges that need to be considered when analyzing and representing them:

1. High dimensionality: Tensors are not limited in the number of dimensions. It becomes difficult to visualize this information in an understandable way when the number of dimensions exceeds four. In addition, analysis becomes more difficult with increasing dimensionality.
2. Sparse data: Depending on the application, individual dimensions of the tensors may contain so-called sparse data. This occurs when most of the entries in this dimension are zero. Sparse data makes it difficult to use linear algebra techniques and should be avoided wherever possible.
3. Non-uniqueness: Tensors can be represented in different ways that are mathematically equivalent but do not look directly identical. This can make interpretation considerably more difficult.
4. Computational complexity: Working with and analyzing tensors is computationally very complex and requires special hardware depending on the dimensionality. Dedicated graphics cards, for example, are suitable for working with large tensors, but they are not always installed as standard and can be expensive to order.
5. Pre-processing of the data: In the rarest of cases, data sets are already available in tensor form. For this reason, functions must be created during pre-processing to convert the data. These functions can quickly become complex and computationally intensive.
6. Evaluation: Results in tensor form are difficult to interpret, especially when it comes to complex and multidimensional data.

Although working with tensors is complex and computationally intensive, tensor analysis is making progress and the results of analyzing multidimensional data are improving. Further developments will follow in the future, which will simplify the work and mean additional progress in the field of machine learning.

This is what you should take with you

• Tensors are mathematical objects from linear algebra and are used to represent multidimensional objects.
• They can be used to perform the same arithmetic operations that are already familiar with vectors or matrices, for example.
• In Machine Learning, they are used, for example, to achieve better recommendations or to map images and videos in data structures.
• However, problems can arise in the evaluation, as one often has to deal with high dimensionality and sparse data.

Thanks to Deepnote for sponsoring this article! Deepnote offers me the possibility to embed Python code easily and quickly on this website and also to host the related notebooks in the cloud.

Other Articles on the Topic of Tensors

• Good Introduction from TensorFlow