Die Korrelation bezeichnet das Verhältnis zwischen zwei statistischen Variablen. Die beiden Variablen sind dann voneinander abhängig und ändern sich gemeinsam. Eine positive Korrelation zweier Variablen bedeutet also, dass eine Steigerung von A auch zu einer Steigerung von B führt. Die Abhängigkeit ist dabei ungerichtet. Es gilt also auch im umgekehrten Fall und eine Steigerung der Variable B verändert auch die Steigung von A im gleichen Umfang.

Eine Kausalität hingegen beschreibt einen Ursache-Wirkungs-Zusammenhang zwischen zwei Variablen. Eine Kausalität zwischen A und B bedeutet also, dass die Steigerung in A auch die Ursache für die Erhöhung von B ist. 

Was ist der Unterschied zwischen Korrelation und Kausalität?

Der Unterschied wird an einem einfachen Beispiel schnell deutlich. Eine Studie könnte sehr wahrscheinlich einen positiven Zusammenhang zwischen dem Hautkrebsrisiko eines Menschen und der Anzahl an Freibadbesuchen finden. Wenn eine Person also häufig das Freibad besucht, dann erhöht sich auch ihr Risiko an Hautkrebs zu erkranken. Eine eindeutige positive Abhängigkeit. Doch besteht auch eine Kausalität zwischen Freibadbesuchen und Hautkrebs? Wahrscheinlich eher nicht, denn das würde bedeuten, dass alleinig der Freibadbesuche die Ursache für das erhöhte Hautkrebsrisiko sind.

Vielmehr ist es so, dass Menschen, die sich häufiger im Freibad aufhalten auch deutlich mehr Sonneneinstrahlung ausgesetzt sind. Wenn dann nicht ausreichend mit Sonnencreme oder ähnlichem vorgesorgt wird, kann es zu mehr Sonnenbränden kommen und diese erhöhen das Hautkrebsrisiko. Man sieht deutlich, dass die Korrelation zwischen Freibadbesuchen und Hautkrebsrisiko keine Kausalität sind. 

Eine Vielzahl von kuriosen Zusammenhängen, die sehr wahrscheinlich keine Kausalität aufzeigen, finden sich auf tylervigen.com.

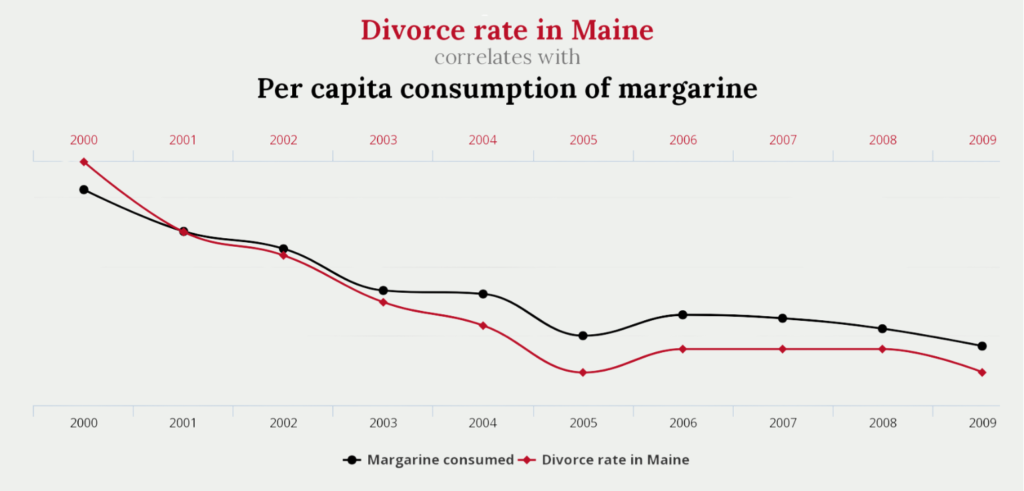
Es besteht beispielsweise eine sehr hohe Abhängigkeit zwischen der Scheidungsrate im amerikanischen Bundesstaat Maine und dem Pro-Kopf-Konsum von Margarine. Ob es sich dabei auch um eine Kausalität handelt, kann man bezweifeln.

Welche Arten der Korrelation gibt es?

Im Allgemeinen unterscheidet man zwei Arten von Zusammenhängen, die unterschieden werden können:

1. Linear oder Nicht-Linear: Die Abhängigkeiten sind linear, wenn die Änderungen in der Variablen A immer eine Änderung mit einem konstanten Faktor bei der Variablen B auslöst. Wenn dies nicht der Fall ist, spricht man von einer nicht-linearen Abhängigkeit. Eine lineare Korrelation besteht beispielsweise zwischen der Körpergröße und dem Körpergewicht. Mit jedem neu gewonnen Zentimeter an Körpergröße nimmt man sehr wahrscheinlich auch eine feste Menge an Körpergewicht zu, solange sich die Statur nicht ändert. Ein nicht-linearer Zusammenhang besteht beispielsweise zwischen der Umsatzentwicklung und der Aktienkursentwicklung eines Unternehmens. Mit der Zunahme des Umsatzes um 30 % wird sich der Aktienkurs womöglich noch um 10 % erhöhen, hingegen bei den darauffolgenden 30 % Umsatzsteigerung wird der Aktienkurs möglicherweise nur noch um 5 % zulegen.
2. Positiv oder Negativ: Wenn die Steigerung der Variablen A zu einer Steigerung der Variablen B führt, dann ist eine positive Korrelation gegeben. Wenn hingegen die Steigerung von A zu einer Abnahme von B führt, dann ist die Abhängigkeit negativ.

Um diese Zusammenhänge auch numerisch ausdrücken zu können, wird der sogenannte Korrelationskoeffizient betrachtet. Im nächsten Kapitel beschäftigen wir uns genauer damit, wie man diesen berechnen kann.

Wie wird die Pearson Korrelation berechnet?

Der Pearson-Korrelationskoeffizient wird am häufigsten genutzt, um die Stärke der Korrelation zwischen zwei Variablen zu bemessen. Diesen kann man ganz einfach mithilfe der folgenden Werte berechnen:

1. Mittelwertberechnung für beide Variablen
2. Berechnung der Standardabweichungen
3. Abweichung vom Mittelwert: Für jedes Element der beiden Variablen muss die jeweilige Abweichung vom Mittelwert berechnet werden.
4. Multiplizieren der Abweichungen: Elementweise werden dann die Abweichungen miteinander multipliziert und dies für alle Elemente der Datensätze aufsummiert.
5. Teilen durch Standardabweichung: Diese Berechnung wird abschließend noch durch das Produkt aus den beiden Standardabweichungen und der Anzahl der Datensätze, die um eins verringert ist, geteilt.

In Kurzform sieht die entsprechende Formel dann wie folgt aus:

\(\) \[r = \frac{ \sum_{i \in D}(x_{i} – \text{mean}(x)) \cdot (y_{i} – \text{mean}(y))}{(n-1) \cdot SD(x) \cdot SD(y)}\]

dabei:

• Σ repräsentiert die Summe über alle Observation in den Datensätzen hinweg.
• xi und yi sind die individuellen Observationen für die Variablen x und y.
• mean(x) und mean(y) sind die Mittelwerte für die Variablen x und y.
• SD(x) und SD(y) sind die einzelnen Standardabweichungen.
• n ist die Anzahl der Observationen und n-1 entsprechend die Anzahl um eins verringert.

Was ist der (Pearson) Korrelationskoeffizient und wie interpretiert man ihn?

Der Korrelationskoeffizient gibt an, wie stark die Abhängigkeit zwischen den beiden Variablen ausgeprägt ist. Im Beispiel von tylervigen.com ist diese Korrelation mit 99,26 % sehr stark ausgeprägt und bedeutet, dass die beiden Variablen sich nahezu 1 zu 1 bewegen, also eine Steigerung des Margarinekonsums um 10 % führt auch zu einer Steigerung der Scheidungsrate um 10 %. In dem oben gezeigten Screenshot ist dies verdeutlicht, da der Margarinekonsum und die Scheidungsrate nahezu parallel abnehmen. Somit zeigt, dass eine Abnahme des Margarinekonsums auch zur Abnahme der Scheidungsrate führt.

Der Korrelationskoeffizient kann dabei auch negativer Werte annehmen. Ein Korrelationskoeffizient kleiner 0 beschreibt die Antikorrelation und sagt aus, dass sich die beiden Variablen gegensätzlich verhalten. Eine negative Abhängigkeit besteht beispielsweise zwischen dem aktuellen Alter und der verbleibenden Lebenserwartung älter man wird, desto geringer ist die noch verbleibende Lebenserwartung eines Menschen. 

Eine Korrelation mit dem Koeffizienten Null hingegen besagt, dass keine Abhängig zwischen den beiden Werten besteht und diese somit nicht korreliert sind.

Welche Korrelationskoeffizienten gibt es?

Die Korrelation bezeichnet ein grundlegendes Konzept in der Statistik, welches die Beziehung zwischen zwei Variablen misst und quantifiziert. Es zeigt dabei nicht nur die Richtung des Zusammenhangs an, sondern ermittelt auch den Faktor an, wie stark die Änderung in der einen Variable zu einer Änderung der anderen Variablen führt. Abhängig vom Zusammenhang, der zwischen den Variablen besteht, gibt es verschiedene Möglichkeiten den konkreten Korrelationskoeffizienten zu berechnen. In diesem Abschnitt werden wir uns die drei weit verbreiteten Methoden zur Berechnung der Korrelation genauer anschauen. 

Pearson-Korrelation

Die Pearson-Korrelation wird am häufigsten verwendet, um die Stärke der linearen Beziehung zwischen zwei Variablen zu quantifizieren. Sie kann jedoch nur verwendet werden, wenn angenommen wird, dass die beiden Kenngrößen linear voneinander abhängen und außerdem metrisch skaliert sind, also numerische Werte besitzen. 

Wenn diese Annahmen gegeben sind, kann die Pearson Korrelation mithilfe von dieser Formel berechnet werden: 

\(\) \[r_{xy} = \frac{\sum (X_i – \overline{X})(Y_i – \overline{Y})}{\sqrt{\sum (X_i – \overline{X})^2} \sqrt{\sum (Y_i – \overline{Y})^2}} \]

Hierbei sind \(X_i\) und \(Y_i\) die Werte der beiden Variablen und \(\overline{X}\) und \(\overline{Y}\) die Mittelwerte der Variablen. Zusätzlich kann diese Formel auch umgeschrieben werden, sodass sie im Nenner die Standardabweichung nutzt: 

\(\) \[r = \frac{ \sum_{i \in D}(x_{i} – \text{mean}(x)) \cdot (y_{i} – \text{mean}(y))}{(n-1) \cdot SD(x) \cdot SD(y)}\]

Die resultierenden Werte liegen dann zwischen -1 und 1, wobei positive Werte auf eine positive Korrelation hindeuten und negative Werte entsprechend auf eine negative Korrelation.

Spearman-Korrelation

Die Spearman-Korrelation erweitert die Annahmen der Pearson-Korrelation und untersucht allgemein die monotone Beziehung zwischen zwei Variablen, ohne jedoch eine lineare Beziehung zu unterstellen. Viel allgemeiner untersucht sie, ob eine Änderung in einer Variablen zu einer Änderung der anderen Variablen führt, auch wenn dieser Zusammenhang nicht linear sein muss. Dadurch eignet sie sich nicht nur für Datensätze mit nichtlinearen Abhängigkeiten, sondern auch für sogenannte ordinale Daten, also Datensätze in denen lediglich die Reihenfolge der Datenpunkte eine wichtige Rolle spielt, nicht aber der genaue Abstand. 

Die Formel für die Spearman-Korrelation basiert auch maßgeblich auf dieser Rangfolge. Dazu werden die Datensätze zuerst nach der ersten Variablen und anschließend nach der zweiten Variable sortiert. Für beide Rangfolgen werden die Ränge beginnend mit 1 für den geringsten Wert durchnummeriert. Anschließend wird für jeden Datenpunkt die Differenz zwichen dem Rang für die erste Variable und dem Rang für die zweite Variable berechnet:

\(\) \[ d_i​ = \text{Rang}(X_i​) − \text{Rang}(Y_i​) \]

Der Spearman Korrelationskoeffizient errechnet sich dann mithilfe der folgenden Formel, wobei \(d\) die erklärte Differenz für jeden Datenpunkt ist und \(n\) die Anzahl der Datenpunkte im Datensatz. 

\(\) \[\rho = 1 – \frac{6 \sum d_i^2}{n(n^2 – 1)} \]

Kendall-Tau-Korrelation

Die Kendall-Tau-Korrelation ist eine weitere Methode, um einen Korrelationskoeffizienten zu bestimmen. Analog zur Spearman Korrelation kann sie nicht-lineare Beziehungen zwischen den Daten quantifizieren und arbeitet auf den ordinalen Beziehungen zwischen den Daten. Im Vergleich zur Spearman Korrelation eignet sie sich besonders bei kleineren Datensätzen und erfasst die Stärke der Beziehung etwas genauer. 

Die Kendall-Tau-Korrelation betrachtet immer Paare von Datenpunkten und unterscheidet dabei konkordante und diskordante Paare. Ein konkordantes Paar an Datenpunkten ist gegeben, wenn ein Paar von Beobachtungen \((x_i, y_i)\) und \((x_j, y_j)\) in der Rangfolge beider Variablen übereinstimmt. Es muss also gelten, dass wenn \((x_i > y_i)\), dann gilt auch \((x_j > y_j)\). Stimmt die Rangfolge hingegen nicht überein, dann gilt das Paar als diskordant. 

Die Formel zur Berechnung der Kendall-Tau-Korrelation ergibt sich dann mithilfe der folgenden Formel: 

\(\) \[\tau = \frac{(\text{Anzahl der konkordanten Paare}) – (\text{Anzahl der diskordanten Paare})}{\frac{1}{2}n(n-1)}\]

Welche Probleme gibt es bei der Untersuchung von Korrelation und Kausalität?

Bei der Erforschung der Zusammenhänge zwischen zwei Variablen, sollte man sich die häufig vorkommenden Probleme vor Augen führen, damit es zu keinen Fehlinterpretationen oder falschen Ergebnissen kommt.

Ein klassischer Fehler ist hierbei, aus einer Korrelation heraus auf eine Kausalität zu schließen. Eine Korrelation beschreibt lediglich, dass zwischen zwei Variablen eine Beziehung besteht, die dazu führt, dass eine Änderung der einen Variablen zu einer Änderung der anderen Variablen führt. Dies kann, muss aber nicht, eine Kausalität bedeuten. Um eine einwandfreie Kausalität nachzuweisen, Bedarf es zusätzliche Beweise, die über randomisierte Experimente erhalten werden können und meist sehr aufwendig sind.

Ein weiteres Problem kann die umgekehrte Kausalität sein, bei der die Richtung der Kausalität falsch interpretiert wird. In einem solchen Fall kann es passieren, dass die angenommene Wirkung der Kausalität tatsächlich die Ursache der Kausalität ist. Das beschriebene Beispiel der vermeintlichen Kausalität zwischen Eiskonsum und Hautkrebserkrankungen ist eine umgekehrte Kausalität, da die vermeintliche Ursache, nämlich der Konsum der Eiscreme, in Wirklichkeit auch eine Wirkung ist.

Bei der Untersuchung der Korrelation sollten Störvariablen bedacht werden, um korrekte Zahlen für die Korrelation zu erhalten. Bei Störvariablen handelt es sich um dritte Variablen, die sowohl einen Einfluss auf die Ursache als auch auf die Wirkung haben. Wenn diese nicht berücksichtigt werden, kann dies zu verfälschten Korrelationskoeffizienten führen. Eine multivariate Analyse, die mehr als zwei Variablen berücksichtigt, kann dabei Abhilfe schaffen.

Nicht ganz so bekannt, wie die bisher genannten Probleme, ist der Post-hoc Fehlschluss bei dem fälschlicherweise eine Kausalität vermutet wird, weil eine zeitliche Abfolge zwischen den Ereignissen besteht. Nur weil ein Ereignis auf ein anderes folgt, ist dies nicht unbedingt eine Wirkung. Es kann andere Gründe geben, die zu dieser beobachteten Beziehung führen.

Das Simpson – Paradoxon tritt auf, wenn die Daten in mehrere Gruppen unterteilt sein und zwischen den Gruppen eine Korrelation beobachtet wird. Das Paradoxon beschreibt den Umstand, dass diese Korrelation sich umkehrt oder sogar verschwindet wenn diese Gruppen kombiniert werden. Deshalb sollte in der Analyse die Auswirkungen von Gruppenzuordnungen beachtet werden, da diese einen Einfluss auf die Korrelation zwischen Variablen haben können.

Als ökologischer Trugschluss bezeichnet man den Fehler, dass Schlussfolgerungen auf Einzelpersonen gezogen werden, anhand von Korrelationen, die auf Gruppenebene gefunden wurden. Mit solchen Vorhersagen sollte man sich Allgemein zurückhalten, da statistische Rückschlüsse auf Einzelpersonen häufig zu falschen Annahmen führen.

Ein weiterer, aber häufiger, Fallstrick ist die Auslassung von Variablen, auch Omitted Variable Bias genannt. Es kann zu falschen Berechnungen beim Korrelationskoeffizient kommen, wenn wichtige Variablen, die eine Beziehung aufweisen, weggelassen werden. Deshalb sollten vor der Analyse immer alle Faktoren bedacht werden, die messbar sind und mit den Untersuchungen im Zusammenhang stehen. Wenn diese weggelassen werden, kann es zu schlichtweg falschen Ergebnissen kommen.

Diese Probleme sollten vor Erstellung einer Studie oder eines Experiments bekannt sein, um diese Fehler zu vermeiden und aussagekräftige Daten zu erhalten.

Wie weist man eine Kausalität nach?

Um eine Kausalität verlässlich nachweisen zu können werden wissenschaftliche Experimente durchgeführt. Darin versucht man Menschen oder Versuchsobjekte in Gruppen aufzuteilen (wie das genau passiert kannst du in unserem Beitrag zu Sampeln nachlesen), sodass im Optimalfall alle Merkmale der Teilnehmer ähnlich oder identisch sind bis auf das Merkmal, das als Ursache vermutet wird.

Für den „Hautkrebs-Freibad-Fall“ bedeutet das konkret, dass versucht wird zwei Gruppen zu bilden in denen beide Teilnehmerkreise in wichtigen Merkmalen, wie Alter, Geschlecht, körperliche Gesundheit und auch ausgesetzte Sonneneinstrahlung pro Woche ähnliche oder am besten sogar gleiche Ausprägungen aufweisen. Nun wird untersucht, ob die Freibadbesuche der einen Gruppe (Merke: die ausgesetzte Sonneneinstrahlung muss konstant bleiben),  das Hautkrebsrisiko im Vergleich zu der Gruppe, die nicht ins Freibad gegangen ist, verändert. Wenn diese Veränderung ein gewisses Level übersteigt, kann man von einer Kausalität reden.

Warum sind Experimente wichtig, um eine Kausalität nachzuweisen?

Nur mithilfe von sogenannten randomisierten, kontrollierten Studien (kurz: RCTs) lassen sich wirkliche Kausalitäten finden und nachweisen. Hier sind einige wichtige Gründe, weshalb diese Experimente für einen Kausalitätsnachweis unerlässlich sind:

• Kontrolle: Nur bei einem Experiment können mögliche Störfaktoren kontrolliert werden, die einen Einfluss auf die Ergebnisvariablen haben. Bei einer Studie werden die Teilnehmer zufällig (randomisiert) einer sogenannten Behandlungs- und Kontrollgruppe zugewiesen. Lediglich die Behandlungsgruppe wird dann der Einflussvariablen ausgesetzt, um die Kausalität zu ermitteln. Dadurch wird sichergestellt, dass die Auswirkungen lediglich durch die Einflussvariable hervorgerufen wurden und nicht auf Unterschieden zwischen den Gruppen basieren.
• Replikation: Durch die genaue Versuchsbeschreibung können RCTs einfach von anderen Forschern repliziert und nachgestellt werden. Dadurch lässt sich untersuchen, ob bei nochmaliger Durchführung dieselben oder ähnliche Ergebnisse erzielt werden, was wiederum die Robustheit der Ergebnisse erhöht und die Verallgemeinerbarkeit unterstreicht.
• Genauigkeit: Nur in Experimenten werden alle möglichen Störvariablen gemessen, soweit dies möglich ist, wodurch die Genauigkeit der Ergebnisse höchstmöglich ist.
• Ethische Erwägungen: Um unethische Entscheidungen und falsche Schlussfolgerungen zu vermeiden, sollten Kausalzusammenhänge nicht nur auf Beobachtungsstudien beruhen. Dies kann zu falschen Vorverurteilungen führen.
• Politische Implikationen: In vielen Fällen basieren politische Entscheidungen auf kausalen Zusammenhängen. Um zu vermeiden, dass schwerwiegende Gesetzesänderungen oder Verbote lediglich auf Korrelationen beruhen, sollten diese vielmehr in unabhängigen und aussagekräftigen Experimenten bestätigt werden.
• Wissenschaftlicher Fortschritt: Durch RCTs können neue Erkenntnisse in der Wissenschaft gemacht werden, die für andere Forscher verständlich und interpretierbar sind. Dabei werden Experimente genutzt, um Hypothesen zu testen und neue Vorschläge anzustellen, die unser gesamtes Leben verändern und verbessern können.

Abschließend lässt sich zusammenfassen, dass Experimente und vor allem RCTs unerlässlich sind, um eine Kausalität nachzuweisen und deren Stärke zu berechnen. Vor allem in Bereichen wie der Medizin, Psychologie und Wirtschaft führen solche Untersuchungen zu deutlich besseren Ergebnissen und belastbaren Zahlen. Beobachtungsstudien hingegen sind zwar wichtig, um Vermutungen anzustellen oder erste Hypothesen zu formulieren, sind jedoch von der Aussagekraft deutlich geringer einzustufen.

Das solltest Du mitnehmen

• Nur in sehr wenigen Fällen bedeutet eine Korrelation auch eine Kausalität.
• Korrelation bedeutet, dass sich zwei Variablen immer gemeinsam ändern. Kausalität hingegen bedeutet, dass die Änderung einer Variablen die Ursache ist für die Änderung der anderen.
• Der Korrelationskoeffizient gibt die Ausprägungsstärke der Abhängigkeit an. Er kann sowohl positiv als auch negativ sein. Bei einem negativen Koeffizienten spricht man von Antikorrelation.
• Um eine Kausalität nachzuweisen benötigt man aufwendige Experimente. 

Andere Beiträge zum Thema Korrelation und Kausalität

• Ausführliche Definitionen zu den Begrifflichkeiten findest Du hier.