What is Gibbs Sampling?

Gibbs sampling is a fundamental and versatile technique in Bayesian statistics and machine learning. It’s widely used for solving complex problems where traditional methods may fail. In this comprehensive guide, we’ll delve deep into Gibbs sampling, exploring its principles, applications, advantages, and how to implement it.

Gibbs sampling is a Markov chain Monte Carlo (MCMC) method used to draw samples from complex probability distributions, particularly those with many variables. It’s named after the physicist Josiah Willard Gibbs. The key idea behind Gibbs sampling is to sample each variable of a multivariate distribution conditionally on the values of all other variables. By iteratively updating one variable at a time, this sampling eventually converges to the target distribution.

Why does Gibbs Sampling matters in Bayesian Inference?

Bayesian inference, a foundational approach in the realm of statistics and probabilistic modeling, is centered on constructing models that express the relationships between observed data, latent variables, and model parameters. When dealing with complex models lacking analytical solutions for parameter estimation, Gibbs sampling emerges as a versatile and powerful technique for estimating posterior probability distributions.

At its core, Bayesian inference seeks to estimate the posterior distribution of model parameters, which represents the updated beliefs about these parameters after assimilating observed data. This is where Gibbs sampling steps in, offering a systematic methodology to draw samples from the joint posterior distribution of all model parameters. Unlike some other Markov chain Monte Carlo (MCMC) methods, Gibbs sampling follows a distinctive approach: it updates one parameter at a time, conditioned on the current values of all other parameters. This sequential, iterative process transforms it into a Markov chain, where each variable undergoes sequential updates based on its posterior distribution given the other variables.

To execute Gibbs sampling effectively, practitioners must derive the conditional posterior distributions for each parameter or latent variable in the model, given all other variables. These conditional distributions can be obtained through analytical or numerical means. With these distributions in hand, the Gibbs sampling algorithm proceeds iteratively. As the number of iterations increases, the samples drawn from the chain progressively converge to the true posterior distribution.

Gibbs sampling is notably well-suited for managing complex models characterized by numerous parameters and intricate dependencies. It simplifies the formidable task of sampling from high-dimensional posterior distributions by breaking it down into a sequence of sequential updates, one parameter at a time. This is a key advantage when dealing with models that encompass intricate structural or conditional relationships.

Practically, Gibbs sampling finds its application in diverse domains such as machine learning, Bayesian data analysis, image processing, and natural language processing. It empowers Bayesian practitioners to confront a wide array of problems by introducing probabilistic and uncertainty modeling, ultimately enabling data-driven, probabilistic, and context-aware solutions. Gibbs sampling is a quintessential tool in the Bayesian toolbox, contributing to the probabilistic understanding of complex phenomena and aiding in robust statistical decision-making.

How does the Gibbs Sampling Process work?

Gibbs sampling is a Markov Chain Monte Carlo (MCMC) technique used for estimating complex probability distributions. It’s particularly valuable in Bayesian statistics and machine learning when the posterior distribution is challenging to compute directly. The method allows us to sample from high-dimensional probability distributions, making it a versatile tool in various fields.

The core idea behind the sampling process is to sample one variable at a time while keeping all other variables fixed. By iteratively updating each variable, we eventually obtain a sequence of samples that converges to the joint distribution of all variables. Here’s a step-by-step breakdown of the sampling process:

1. Initialization: Start with an initial guess for the values of the variables in the model. These initial values can significantly impact the convergence of the Gibbs sampler.

2. Iterative Sampling: The key is the iterative process. In each iteration, select one variable to update, while keeping all others fixed. The choice of the order in which variables are updated can be arbitrary or based on specific criteria.

3. Conditional Distribution: For the selected variable, sample from its conditional distribution given the current values of all other variables. This step requires knowledge of the conditional distribution, which is often available in Bayesian models.

4. Update Values: Replace the current value of the selected variable with the sampled value. Now, the system has new values for this variable, while all other variables remain unchanged.

5. Repeat: Continue this iterative process for a large number of iterations or until convergence is achieved. Convergence is typically assessed by examining the stability of the sample sequences.

6. Collect Samples: As the Gibbs sampling process proceeds, it generates a sequence of samples for each variable. These sequences collectively form an approximation of the joint distribution of all variables.

7. Analyze Results: After the Gibbs sampling process is complete, the collected samples can be used to estimate the posterior distribution, calculate posterior means, and variances, and make probabilistic inferences about the model’s parameters.

8. Assess Convergence: Monitoring the convergence of the Gibbs sampler is essential. Convergence diagnostic tools like trace plots, autocorrelation plots, and the Geweke test can help ensure that the generated samples represent the true distribution.

By sampling from the conditional distribution of each variable, while holding the others constant, Gibbs sampling creates a Markov chain that eventually converges to the target distribution. This technique’s effectiveness is particularly evident in situations where the joint distribution is complex, and multidimensional, or where exact solutions are challenging to derive.

The ability to perform Bayesian inference, explore posterior distributions, and estimate complex models makes Gibbs sampling a valuable asset in statistical analysis, machine learning, and data science. Its adaptability to custom models and hierarchical structures further underscores its significance.

What is Convergence and Mixing in Gibbs Sampling?

Convergence and mixing are critical considerations when applying Gibbs sampling, as they determine the reliability and efficiency of the Markov chain generated by this MCMC method. In the context of Gibbs sampling, convergence refers to the idea that as the algorithm progresses, the generated samples approach the true underlying distribution. Mixing, on the other hand, pertains to how well the Markov chain explores the parameter space and samples from different regions efficiently. Let’s delve into these concepts in more detail:

1. Convergence Assessment:

Convergence is the central requirement for any MCMC method to provide reliable results. In Gibbs sampling, assessing convergence involves determining whether the Markov chain has reached a state where the sampled values are close enough to the true posterior distribution.

Common methods for assessing convergence include:

Visual Inspection: Plotting trace plots and autocorrelation plots to check for erratic behavior, and ensuring that the sampled values stabilize over time.
Gelman-Rubin Statistic (R-hat): This statistic compares the variance within and between multiple chains to assess whether they have converged to the same distribution. An R-hat value close to 1 indicates convergence.
Effective Sample Size (ESS): ESS quantifies how many independent samples are equivalent to the autocorrelated samples generated by the Markov chain. Higher ESS values imply better convergence.
Kernel Density Estimation: Plotting kernel density estimates of samples from different chains to visualize the convergence.

2. Mixing in Gibbs Sampling:

Mixing measures the efficiency of the Markov chain in exploring the parameter space. A well-mixed chain efficiently samples from all regions of interest, avoiding situations where the chain gets stuck in local optima or explores the space too slowly.

Factors influencing mixing include:

Parameterization: Choosing appropriate parameterization can significantly impact mixing. It’s essential to select parameterizations that promote efficient transitions between states.
Initial Values: The choice of initial values can affect mixing. If the chain starts far from regions of high probability density, it may require an extended burn-in period to reach the stationary distribution.
Adaptive Sampling: Some adaptive Gibbs sampling algorithms adjust the sampling scheme during the chain’s evolution to improve mixing. For instance, the Metropolis-adjusted Gibbs sampler can be used to adaptively accept or reject proposed samples, aiding in mixing.
Thinning: Sometimes, thinning the Markov chain, i.e., taking only every ‘k’ sample, can reduce autocorrelation and improve mixing. However, this may reduce the effective sample size.

3. Improving Convergence and Mixing:

To address convergence and mixing issues, consider the following strategies:

Increasing the number of iterations (samples) to allow the Markov chain more time to explore and converge.
Experiment with different initialization strategies to ensure the chain starts in a region of high probability density.
Choose more sophisticated proposal distributions that promote efficient mixing and convergence.
Consider alternative MCMC methods like Hamiltonian Monte Carlo (HMC) or Sequential Monte Carlo (SMC) if Gibbs sampling struggles with convergence.

In summary, convergence and mixing are vital aspects of Gibbs sampling. Assessing convergence ensures the reliability of the generated samples while achieving good mixing guarantees that the Markov chain explores the parameter space efficiently. Understanding these concepts and applying appropriate diagnostics is crucial when using Gibbs sampling in practice.

What are the applications of Gibbs Sampling?

Gibbs sampling has a wide range of applications across various fields. Here are a few notable ones:

Probabilistic Graphical Models: Gibbs sampling is used in graphical models like Markov Random Fields (MRFs) and Bayesian networks for tasks such as image denoising, image segmentation, and structure learning.

Latent Variable Models: In cases where some variables are unobserved (latent), it helps in estimating the hidden variables’ values.

Text Analysis: In natural language processing, Gibbs sampling can be applied to topic modeling, document classification, and sentiment analysis.

Bayesian Regression: It’s used to perform Bayesian linear regression, which allows modeling the uncertainty in regression coefficients.

Ising Model: In statistical physics, Gibbs sampling helps simulate the Ising model, which describes the magnetic properties of materials.

What are the advantages and disadvantages of Gibbs Sampling?

Gibbs sampling is a powerful Markov Chain Monte Carlo (MCMC) technique with several advantages that make it a valuable tool for various applications. However, like any method, it comes with certain limitations. Here, we explore both the advantages and disadvantages:

Advantages:

1. Simplicity and Flexibility: Gibbs sampling is conceptually straightforward, particularly when dealing with hierarchical models. It provides a unified framework for Bayesian analysis, simplifying complex problems into more manageable conditional distributions.

2. Approximation of Complex Distributions: Gibbs sampling excels in situations where direct sampling or analytical solutions for complex posterior distributions are infeasible. It effectively deals with high-dimensional spaces.

3. Bayesian Inference: It is a cornerstone of Bayesian statistics. It enables the estimation of posterior distributions, which is crucial for making probabilistic inferences, updating beliefs, and understanding uncertainties.

4. Customizable: The method is highly adaptable to different models and distributions. Practitioners can easily implement Gibbs sampling for models that don’t conform to standard distributions, making it a versatile tool in Bayesian analysis.

5. Convergence: With proper tuning and assessment, Gibbs sampling chains typically converge to the true posterior distribution, making it a reliable approach for estimating unknown parameters.

6. Conditional Independence: The method leverages conditional distributions, which can often lead to faster convergence and efficient sampling. This property is particularly useful when variables in a model exhibit conditional independence.

Disadvantages:

1. Requires Knowledge of Conditional Distributions: Gibbs sampling relies on knowing the conditional distributions of the variables of interest. For complex models, determining these distributions can be challenging and may require considerable domain expertise.

2. Computational Intensity: For high-dimensional problems, the Gibbs sampler can be computationally demanding. It may require a large number of iterations to achieve convergence, which can slow down the sampling process.

3. Mixing Issues: In certain situations, it may suffer from poor mixing, where the Markov chain explores the parameter space too slowly. This can hinder convergence and result in inefficient sampling.

4. Initialization Sensitivity: The quality of the initial values can influence the performance of the Gibbs sampler. Poor initialization can lead to slow convergence or even divergence. Selecting suitable initial values is often a non-trivial task.

5. May Not Be the Best for All Scenarios: While this sampling method is a powerful technique, there are instances where other MCMC methods, like Metropolis-Hastings or Hamiltonian Monte Carlo, may perform better, particularly in highly correlated or non-standard distributions.

In summary, Gibbs sampling is a valuable MCMC technique that simplifies Bayesian analysis, handles complex distributions and provides posterior inference. However, it is not without limitations, particularly in terms of computational intensity, sensitivity to initialization, and challenges in scenarios with multimodal distributions. When applied judiciously and in conjunction with convergence diagnostics, Gibbs sampling remains a powerful method for tackling a wide range of statistical and machine learning problems.

How can you implement the Gibbs Sampling in Python?

Here’s a simple example of implementing Gibbs sampling in Python. We’ll use a bivariate normal distribution for illustration:

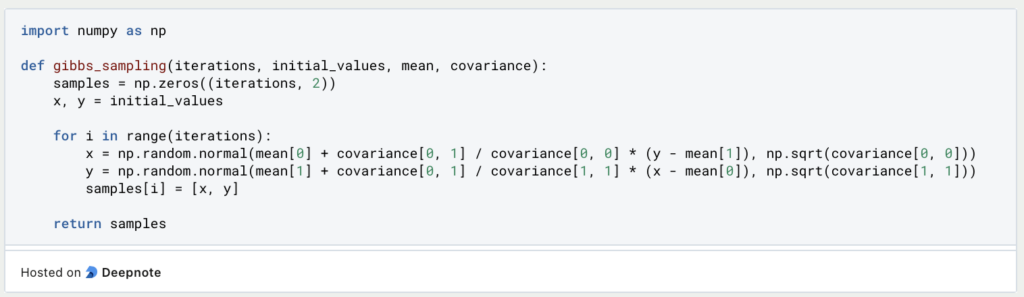
In this example, we’re performing Gibbs sampling to generate samples from a bivariate normal distribution.

What are common variations and enhancements of Gibbs Sampling?

Gibbs sampling is a powerful Markov chain Monte Carlo (MCMC) technique, but it has various variations and enhancements designed to address specific challenges and improve efficiency in different scenarios.

1. Blocked Gibbs Sampling: In standard Gibbs sampling, variables are sampled one at a time sequentially. Blocked Gibbs sampling, on the other hand, groups variables into blocks and samples all the variables within a block simultaneously. This can lead to faster convergence, especially in cases where variables are highly dependent.

2. Adaptive Gibbs Sampling: In this approach, the proposal distribution for each variable is updated during the sampling process based on the past samples. This adaptability can improve the mixing of the Markov chain and lead to a more efficient exploration of the posterior distribution.

3. Slice Sampling: Slice sampling is a variation that addresses challenges in selecting the width of the proposal distribution. It eliminates the need to specify proposal widths, making it more straightforward for users.

4. Collapsed Gibbs Sampling: Collapsed Gibbs sampling is used when certain variables in a model are integrated out rather than sampled. This reduces the dimensionality of the problem and can be more efficient in certain cases. It is often employed in latent variable models like Latent Dirichlet Allocation (LDA).

5. Nonparametric Bayesian Models: This sampling approach can be extended to nonparametric Bayesian models, such as the Dirichlet Process, Indian Buffet Process, and Chinese Restaurant Process. These models allow for a flexible number of clusters or groups, making Gibbs sampling applicable in a wide range of data clustering and classification problems.

6. Hybrid Sampling Methods: Researchers often combine Gibbs sampling with other MCMC methods to create hybrid samplers that leverage the strengths of both approaches. For instance, Gibbs sampling can be used within a Metropolis-Hastings framework to enhance the exploration of complex distributions.

The choice of which Gibbs sampling variation or enhancement to use depends on the specific problem and its characteristics. Practitioners need to consider the nature of the data, the model, and computational constraints when selecting the most appropriate Gibbs sampling approach. These variations and enhancements illustrate the adaptability of Gibbs sampling in addressing a wide range of challenges and making it a versatile tool in Bayesian inference and probabilistic modeling.

This is what you should take with you

Gibbs sampling is a fundamental technique in Bayesian statistics, enabling the estimation of complex posterior distributions and providing a framework for making probabilistic inferences.
The method’s elegance lies in its ability to sample from conditional distributions, simplifying high-dimensional problems into more manageable steps.
Gibbs sampling is highly adaptable to different models and distributions, making it a versatile tool for Bayesian analysis.
In cases where conditional distributions are conjugate to the prior distributions, Gibbs sampling can offer highly efficient sampling.
In high-dimensional spaces, Gibbs sampling can be computationally intensive and may require extensive iterations for convergence.
The quality of initial values can significantly impact the performance of the Gibbs sampler, necessitating careful consideration during implementation.
While Gibbs sampling is powerful, it’s not always the best choice. In cases of poor mixing, multimodal distributions, or non-standard models, other MCMC techniques like Metropolis-Hastings or Hamiltonian Monte Carlo may be more suitable.