Regressionen werden dafür genutzt einen mathematischen Zusammenhang zwischen zwei Variablen x und y herzustellen. Sowohl die Statistik als auch die Grundlagen von Machine Learning beschäftigen sich damit, wie man die Variable y mithilfe einer oder mehreren Variablen x erklären kann. Hier ein paar Beispiele:

• Welchen Einfluss hat die Lerndauer (=x) auf die Klausurnote (=y)?
• Wie hängt die Nutzung von Pflanzendünger (=x) mit der zu tatsächlich erzielten Ernte (=y) zusammen?
• Wie ändert sich die Kriminalitätsrate in einer Stadt (=y) abhängig von der Anzahl an Polizisten in der Stadt (=x)?

Die zu erklärende Variable y wird dabei als abhängige Variable, Kriterium oder Regressand bezeichnet. 

Die erklärende Variable x hingegen ist die sogenannte unabhängige Variable, Prädiktor oder Regressor.

Das Ziel der Linearen Regression ist es, einen mathematischen Zusammenhang zu formulieren, der den Einfluss von x auf y auch in Zahlen beschreibt: 

\(\) \[y = β_0 + β_1x + u \]

• β₀: Schnittpunkt mit der y-Achse, bspw. die Klausurnote, die man erreichen würde ohne zu lernen.
• β₁: Steigerung der Regressionsgeraden, bspw. der Einfluss, den eine zusätzliche Stunde Lernen auf die Klausurnote hat. 
• u: Fehlerterm, bspw. alle Einflüsse, die eine Auswirkung auf die Klausurnote haben, aber nicht über die Lerndauer erfasst werden, bspw. Vorwissen. 
• y: Variable, die man vorhersagen möchte mit hilfe der Linearen Regression.
• x: Variable, die als Grundlage der Vorhersage genutzt wird und eine Auswirkung auf y haben.

Bildlich gesprochen bedeutet dies, dass wir versuchen die Gerade durch die Punktewolke an Datensätzen zu finden, die den geringsten Abstand zu allen Punkten aufweist.

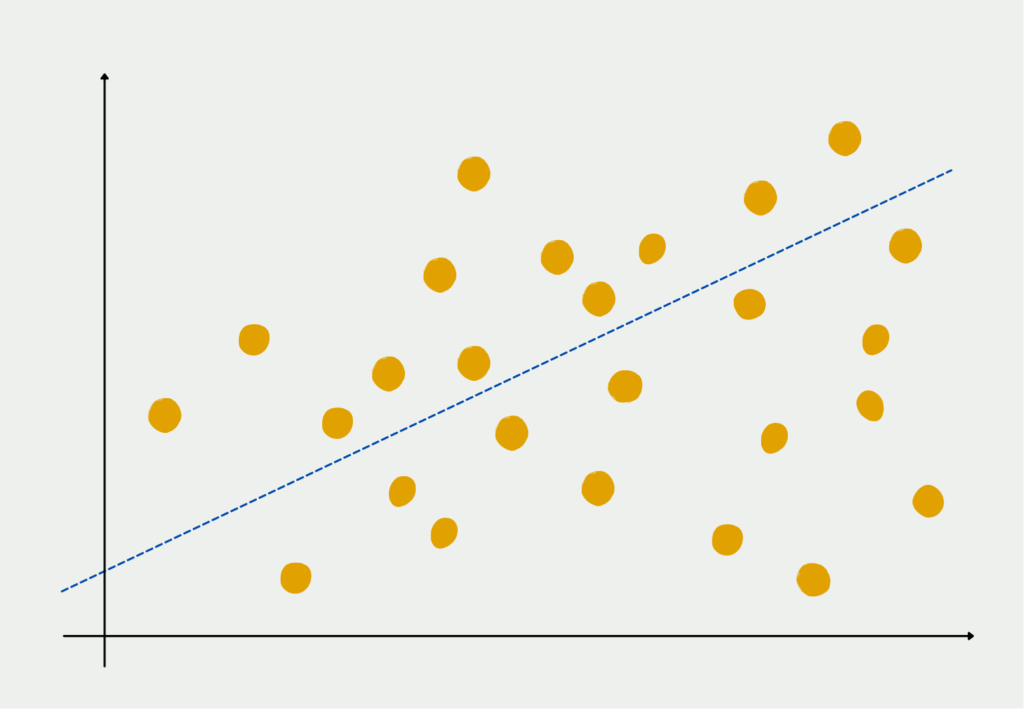
Wie interpretiert man eine Regressionsgleichung?

Angenommen wir erhalten für das Beispiel mit der Klausurvorbereitung die folgende Regressionsgleichung: 

\(\) \[y = 5,0 – 0,2x + u \]

In diesem Fall ist der y-Achsenabschnitt (β₀) 5,0. Das bedeutet, dass die untersuchten Personen ohne eine Stunde zu lernen, die Klausur voraussichtlich mit der Note 5,0 abschließen werden.

Das Regressionsgewicht (β₁) beträgt in diesem Fall -0,2. Somit wird die Klausurnote mit jeder Stunde in der für das Fach gelernt wird um 0,2 Noten besser. Mit 5h Lernaufwand wäre also die voraussichtliche Note des Studenten oder der Studentin um 1,0 besser verglichen mit dem Fall, dass nicht gelernt wurde.  

Insgesamt könnten die Studenten nach dieser Regression nach 10h Lernaufwand mit einer endgültigen Note von 3,0 rechnen. Gleichzeitig können sie ablesen, dass sie mindestens 5h lernen sollten um zu bestehen. 

Welche Annahmen müssen erfüllt sein?

Die lineare Regression ist eine statistische Methode, die die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen modelliert. Die Annahmen der linearen Regression sind:

• Linearität: Die Beziehung zwischen den unabhängigen und abhängigen Variablen sollte linear sein. Das bedeutet, dass sich der Wert der abhängigen Variable proportional zum Wert der unabhängigen Variablen ändert.
• Unabhängigkeit: Die Beobachtungen im Datensatz sollten voneinander unabhängig sein. Mit anderen Worten: Der Wert einer Beobachtung sollte nicht durch den Wert einer anderen Beobachtung beeinflusst werden.
• Homoskedastizität: Die Varianz der Fehler oder Residuen sollte über alle Stufen der unabhängigen Variablen hinweg konstant sein. Dies bedeutet, dass die Streuung der Residuen für alle Werte der unabhängigen Variable gleich sein sollte.
• Normalität: Die Fehler oder Residuen sollten einer Normalverteilung folgen. Das bedeutet, dass die Mehrzahl der Residuen nahe bei Null liegen sollte, und die Anzahl der Residuen, die weit von Null entfernt sind, sollte mit zunehmender Entfernung von Null abnehmen.
• Keine Multikollinearität: Die unabhängigen Variablen sollten nicht stark miteinander korreliert sein. Multikollinearität kann Probleme bei der Interpretation der Regressionskoeffizienten verursachen und zu instabilen und unzuverlässigen Modellen führen.
• Keine Ausreißer: Ausreißer sind Beobachtungen, die sich deutlich von den anderen Beobachtungen im Datensatz unterscheiden. Ausreißer können die Regressionslinie beeinflussen und zu ungenauen Vorhersagen führen.

Es ist wichtig, diese Annahmen zu überprüfen, bevor eine lineare Regression für Vorhersagen verwendet wird. Verstöße gegen diese Annahmen können zu verzerrten Schätzungen und ungenauen Vorhersagen führen.

Was ist die Fehlerkonstante?

In unseren bisherigen Ausführungen wurde auf den Fehlerterm u nicht genauer eingegangen, obwohl er eine entscheidende Bedeutung hat für die Interpretation der Regression. Wenn wir für eine Regression lediglich ein oder zwei unabhängige Variablen nutzen wird dies in vielen Fällen nicht ausreichen, um alle Einflussfaktoren auf die abhängige Variable y abzubilden. Natürlich ist nicht du die Anzahl der gelernten Stunden ausschlaggebend für die finale Klausurnote. Es gibt noch einige andere Faktoren, die dort mit reinspielen bspw. der Umgang mit Stresssituationen oder die Zahl der besuchten Vorlesungen. 

Dieser Umstand ist erstmal nicht schlimm, da wir nur die unabhängigen Variablen wählen, die für unsere Auswertung von Interesse sind. In unserem Beispiel wollen wir nur explizit eine Aussage treffen über den Zusammenhang zwischen Lernen und der Prüfungsnote. Deshalb müssen wir die Zahl der besuchten Vorlesungen nicht explizit als Variable aufführen, sondern können sie als eine von vielen in der Fehlerkonstante belassen. 

Kritisch wird es jedoch dann, wenn die unabhängige Variable “Lernstunden” mit einem Faktor korreliert (siehe Korrelation und Kausalität), der noch in der Fehlerkonstanten versteckt ist. Dann ist der Regressionsfaktor (β₁) nicht korrekt und wir machen einen Fehler in der Interpretation. 

Angenommen wir wollen bestimmen, wie sich der Bildungsgrad auf den Lohn pro Stunde auswirkt. Dazu nutzen wir die Bildung in Jahren als unabhängige Variable x und den aktuellen Stundenlohn als abhängige Variable y:

\(\) \[\text{Stundenlohn} = β_0 + β_1 \cdot \text{(Bildung in Jahren)} + u \]

Im Fehlerterm wären in diesem Beispiel Faktoren wie Betriebszugehörigkeit, Anzahl der Beförderungen oder allgemeine Intelligenz. In diesem Fall kann es zu Problemen kommen, wenn wir mit hilfe dieser Gleichung β₁ als Einfluss interpretieren, den ein zusätzliches Jahr Bildung auf den Stundenlohn hat. Der Faktor Intelligenz ist nämlich sehr wahrscheinlich mit der Variablen Bildung positiv korreliert. Eine Person mit einem höheren Intelligenzquotienten wird sehr wahrscheinlich auch einen höheren Bildungsabschluss besitzen und somit mehr Jahre in der Schule oder an der Universität verbracht haben.

Welche Anwendungen nutzen diese Modellart?

Die lineare Regression ist eine beliebte statistische Methode zur Modellierung der Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen. Die Technik ist in vielen Bereichen und Branchen weit verbreitet und findet sowohl in der Forschung als auch in der Wirtschaft zahlreiche Anwendungen.

Eine der häufigsten Anwendungen der linearen Regression findet sich im Bereich der Wirtschaftswissenschaften. In Wirtschaftsmodellen wird die lineare Regression häufig verwendet, um die Beziehung zwischen zwei oder mehr wirtschaftlichen Variablen zu schätzen, z. B. Einkommen und Ausgaben oder Arbeitslosigkeit und Inflation. Auf diese Weise können Wirtschaftswissenschaftler Vorhersagen über künftige Wirtschaftstrends treffen und Strategien zur Lösung wirtschaftlicher Probleme entwickeln.

Die lineare Regression wird auch häufig im Finanzbereich eingesetzt. Sie kann beispielsweise zur Modellierung der Beziehung zwischen Aktienkursen und verschiedenen Wirtschaftsindikatoren oder zur Analyse des Risikos und der Rendite verschiedener Anlageportfolios verwendet werden.

Im Marketingbereich kann die lineare Regression zur Modellierung des Verhältnisses zwischen den Marketingausgaben eines Unternehmens und seinen Verkaufserlösen verwendet werden. Auf diese Weise können Unternehmen ihre Marketingstrategien optimieren und Ressourcen effizienter zuweisen.

Die lineare Regression wird auch in den Gesundheitswissenschaften, insbesondere in der medizinischen Forschung, häufig eingesetzt. Sie kann beispielsweise dazu verwendet werden, die Beziehung zwischen einer bestimmten Krankheit und verschiedenen Risikofaktoren wie Alter, Geschlecht und Lebensstil zu analysieren. Auf diese Weise können Forscher mögliche Krankheitsursachen ermitteln und Strategien zur Prävention und Behandlung entwickeln.

Im Bereich der Sozialwissenschaften wird die lineare Regression häufig zur Analyse der Beziehung zwischen verschiedenen sozialen und verhaltensbezogenen Variablen wie Bildung, Einkommen und Gesundheitszustand verwendet. Auf diese Weise können Forscher soziale und wirtschaftliche Ungleichheiten besser verstehen und Maßnahmen zu deren Beseitigung entwickeln.

Insgesamt ist die lineare Regression ein vielseitiges und breit anwendbares statistisches Verfahren, das zur Modellierung und Analyse von Beziehungen zwischen Variablen in einer Vielzahl von Bereichen und Kontexten eingesetzt werden kann. Ihre Flexibilität und Einfachheit machen sie zu einer beliebten Wahl sowohl für Forscher als auch für Unternehmensanalysten.

Was sind die Herausforderungen bei einer linearen Regresssion?

Die lineare Regression hat mehrere Einschränkungen, darunter:

• Nur lineare Beziehungen: Bei der linearen Regression wird davon ausgegangen, dass die Beziehung zwischen den abhängigen und unabhängigen Variablen linear ist. Das heißt, wenn die Beziehung nicht linear ist, passt das Modell möglicherweise nicht gut zu den Daten.
• Anfälligkeit für Ausreißer: Bei diesem Regressionsmodell reagiert empfindlich auf Ausreißer, d. h. auf Datenpunkte, die erheblich vom Rest der Daten abweichen. Ausreißer können einen großen Einfluss auf die Steigung und den Achsenabschnitt der Linie haben, was zu ungenauen Vorhersagen führen kann.
• Multikollinearität: Die lineare Regression geht davon aus, dass die unabhängigen Variablen nicht stark miteinander korreliert sind. Liegt Multikollinearität vor, d. h. zwei oder mehr unabhängige Variablen sind stark korreliert, kann das Modell die einzelnen Auswirkungen der einzelnen Variablen möglicherweise nicht unterscheiden.
• Überanpassung oder Unteranpassung: Wenn das Modell zu komplex ist, kann es sich zu stark an die Daten anpassen, d. h. es passt sich eher dem Rauschen in den Daten an als dem zugrunde liegenden Muster. Wenn das Modell zu einfach ist, kann es die Daten nicht richtig abbilden, d. h., es vernachlässigt wichtige Beziehungen zwischen den Variablen.

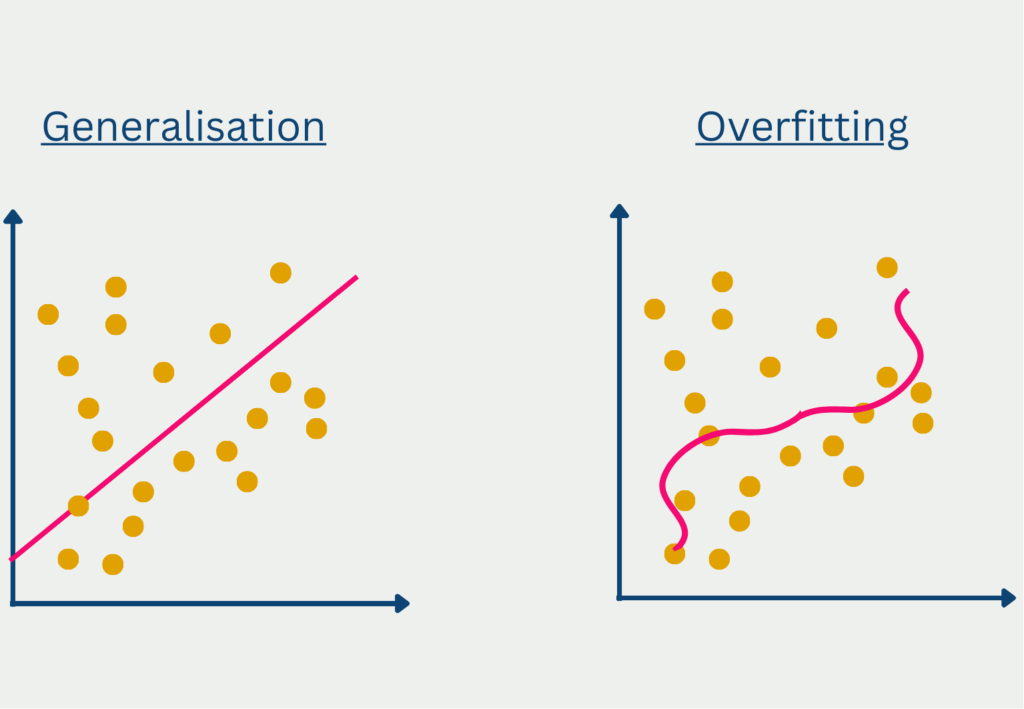
• Annahme der Unabhängigkeit: Bei dieser Regressionsart wird davon ausgegangen, dass die Beobachtungen unabhängig voneinander sind. Wenn die Beobachtungen nicht unabhängig sind, wie z. B. bei Zeitreihen, ist das Modell möglicherweise nicht geeignet.

Es ist wichtig, diese Einschränkungen bei der Verwendung der linearen Regression im Auge zu behalten und die Leistung des Modells sorgfältig zu bewerten, um sicherzustellen, dass es für die spezifischen Daten und das jeweilige Problem geeignet ist.

Das solltest Du mitnehmen

• Die Lineare Regression ist ein Spezialfall der Regressionsanalyse.
• Es wird versucht eine lineare Funktion zu finden, die beschreibt, wie die unabhängige Variable x die abhängige Variable y beeinflusst.

Andere Beiträge zum Thema Lineare Regression

• Ein anderes Beispiel für eine Lineare Regression inklusive Video ist hier.
• Die mathematischen Grundlagen sind hier ausführlicher beschrieben, als in unserem Beitrag.