Die Markow Kette ist ein zentrales Konzept in der Mathematik und der Stochastik und wird genutzt, um die Wahrscheinlichkeit von bestimmten Zuständen in stochastischen Prozessen vorherzusagen. Das zentrale Merkmal solcher Systeme ist die sogenannte „Gedächtnislosigkeit“, da die Wahrscheinlichkeit jedes Ereignisses nur vom aktuellen Zustand des Systems abhängt und nicht von der Vergangenheit. 

In diesem Artikel schauen wir uns die zentralen Eigenschaften der Markov Kette genauer an und gehen im Detail auf die mathematische Darstellung ein. Außerdem sprechen wir über reale Beispiele und simulieren ein solches Zustandsmodell in Python. 

Was ist die Markov Kette?

Eine Markow Kette ist ein zentrales Modell in der Wahrscheinlichkeitstheorie, welches sich mit Abfolgen von Zufallsereignissen beschäftigt. Das zentrale Merkmal dieser Kette ist, dass jede Wahrscheinlichkeit eines Ereignisses ausschließlich von dem Zustand abhängt, in dem sich das System gerade befindet. Die vorangegangenen Ereignisse hingegen sind völlig irrelevant für die Wahrscheinlichkeit des nächsten Schritts. Genauer gesagt ist eine Markow Kette also ein Prozess, welcher die Markov-Eigenschaft erfüllt, da sie besagt, dass das zukünftige Verhalten eines Systems nicht von der Vergangenheit, sondern nur vom aktuellen Zustand abhängt. 

Ein klassisches Beispiel für eine Markow Kette ist das Spiel Monopoly. Dabei bewegen sich mehrere SpielerInnen mit einem Würfelwurf über das Spielfeld. In jedem Zug hängt die Wahrscheinlichkeit des zukünftigen Felds ausschließlich vom Würfelwurf und dem aktuellen Feld des Spielers ab. Wie die Spielerin jedoch auf das aktuelle Feld gekommen ist, spielt für das zukünftige Verhalten keine Rolle mehr. 

Welche Begriffe werden im Zusammenhang mit der Markow Kette verwendet?

Bevor wir in die mathematische Definition der Markov Ketten tiefer einsteigen können, müssen wir einige Begrifflichkeiten einführen, die im Bereich der Wahrscheinlichkeitsberechnung im Allgemeinen und im Bereich der Markow Ketten im Besonderen verwendet werden. Zu den wichtigsten Begriffen und Konzepten zählen: 

Zustandsraum

Als Zustandsraum wird die Menge aller möglichen Zustände definiert, die ein System in einer Markow Kette einnehmen kann. Jedes Element in diesem Zustandsraum beschreibt eine konkrete Situation, in der sich das System zu einem beliebigen Zeitpunkt befinden kann. Dabei muss jedoch nicht gegeben sein, dass dieser Zustand im Verlauf des Systems auch wirklich erreicht wird. Dieser Zustandsraum kann sowohl endlich viele Zustände umfassen als auch unendlich viele. 

Beispiele: 

• Ein einfaches Wettermodell beispielsweise sagt lediglich die Werte „Sonne“ oder „Regen“ vorher. Somit umfasst der Zustandsraum eine Menge von zwei Zuständen und wird als {Regen, Sonne} ausgedrückt. 
• Bei Monopoly oder einem anderen Brettspiel umfasst der Zustandsraum alle Felder, die im Laufe des Spiels erreicht werden können. Obwohl ein Feld einen möglichen Zustand im Spielverlauf darstellt, ist nicht sichergestellt, dass in einem Spiel dieses Feld auch wirklich erreicht wird. 
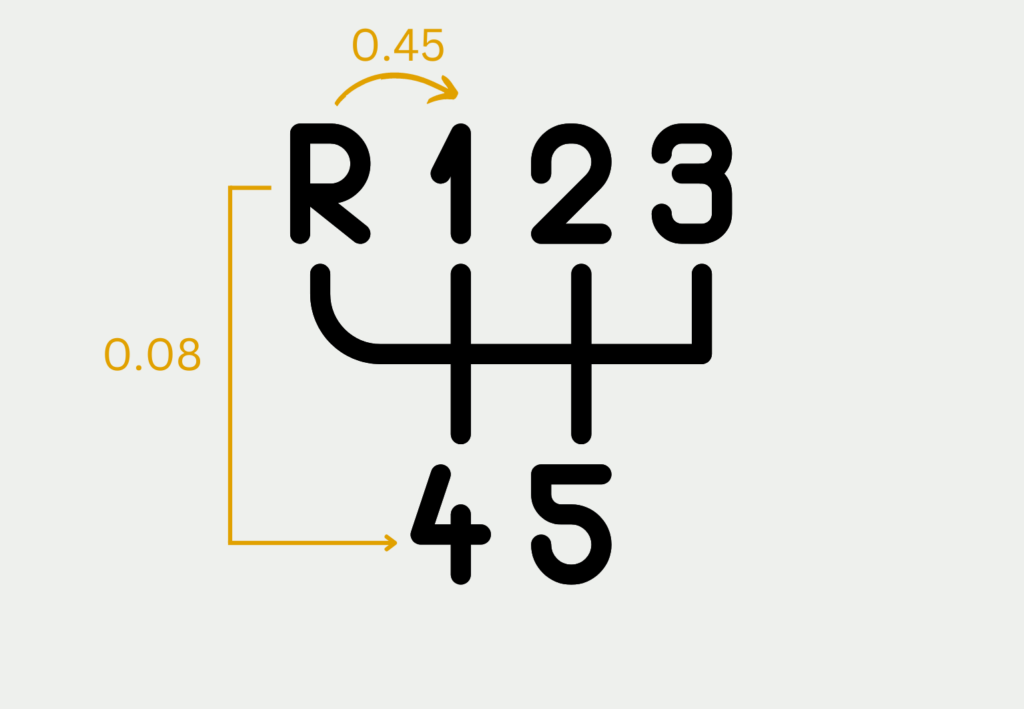
• In einem Schaltwagen umfasst der Zustandsraum des Getriebes alle Gänge, die vorhanden sind, also zum Beispiel {Rückwärtsgang, 1. Gang, 2. Gang, 3. Gang, 4. Gang, 5. Gang}

Übergangswahrscheinlichkeit / Übergangsmatrix

Die Übergangswahrscheinlichkeit beschreibt die Wahrscheinlichkeit, dass das System zu einem Zeitpunkt von einem Zustand in einen anderen Zustand übergeht. Bei der Markow Kette hängt diese Wahrscheinlichkeit aufgrund der Markov Eigenschaft ausschließlich vom aktuellen Zustand des Systems ab und nicht von der Vergangenheit des Systems. Beim Schaltvorgang können diese Wahrscheinlichkeiten zum Beispiel so aussehen, dass es deutlich wahrscheinlicher ist vom Rückwärtsgang in den ersten Gang zu schalten als vom Rückwärtsgang in den vierten Gang. 

In der Übergangsmatrix werden alle Übergangswahrscheinlichkeiten festgehalten, die im nächsten Zustand eingenommen werden können. Dabei müssen sich alle Übergangswahrscheinlichkeiten in einer Zeile auf 1 summieren, sodass sichergestellt ist, dass ein Zustand als nächstes eingenommen wird. Mathematisch gesehen wird die Übergangsmatrix \(P\) für \(n\) Zustände mithilfe einer \(n \times n\) Matrix beschrieben, in der das Element \(p_{i,j}\) die Wahrscheinlichkeit angibt, vom Zustand \(i\) in den Zustand \(j\) überzugehen.  

\(\) \[ P = \begin{pmatrix}
p_{R,R} & p_{R,1} & 0 & 0 & 0 & 0 \\
p_{1,R} & p_{1,1} & p_{1,2} & 0 & 0 & 0 \\
0 & p_{2,1} & p_{2,2} & p_{2,3} & 0 & 0 \\
0 & 0 & p_{3,2} & p_{3,3} & p_{3,4} & 0 \\
0 & 0 & 0 & p_{4,3} & p_{4,4} & p_{4,5} \\
0 & 0 & 0 & 0 & p_{5,4} & p_{5,5}
\end{pmatrix} \]

Dadurch ergibt sich auch eine Übergangsmatrix für den Gangwechsel, wobei wir davon ausgehen, dass keine Gänge übersprungen werden können und beispielsweise vom dritten Gang nur in den zweiten Gang heruntergeschalten oder in den vierten Gang hochgeschalten werden kann. Außerdem gibt es auch die Möglichkeit, dass man im dritten Gang verbleibt, was durch die Wahrscheinlichkeit \(p_{3,3}\) beschrieben wird. 

Diskrete Markow Kette

In einer diskreten Markov Kette werden die Zustände nur zu bestimmten, diskreten Zeitpunkten gewechselt. Das bedeutet, dass das System sich nur zu vorher definierten Zeitpunkten und in typischerweise gleichen Abständen verändert. Beim Monopoly Spiel beispielsweise verändert sich das System Spielfeld immer nur während eines Spielzugs. 

Kontinuierliche Markow Kette

Bei kontinuierlichen Markow Ketten passieren die Zustandsänderungen zu beliebigen Zeitpunkten, die kontinuierliche auf einer Zeitachse liegen. Dies hat zur Folge, dass der Zeitpunkt eines Übergangs rein zufällig ist und von einer Wahrscheinlichkeitsverteilung abhängt. Bei dem Fahren eines Schaltwagens beispielsweise finden die Schaltvorgänge nicht zu festen Zeitpunkten statt, sondern hängen vom Verkehrsfluss und der gefahrenen Geschwindigkeit ab. Dadurch unterliegen sie einer Wahrscheinlichkeitsverteilung.

Mithilfe von diesen grundlegenden Konzepten und Begriffen können wir nun eine Markow Kette allgemein und mathematisch definieren. 

Wie sieht die mathematische Darstellung der Markow Kette aus?

Eine Markow Kette wird mathematisch durch eine eigene Übergangsmatrix \(P\) beschrieben, die sich ganz allgemein, wie folgt definieren lässt: 

\(\)\[P(X_{n+1} = j \mid X_n = i) = p_{ij} \]

Hier ist \(p_{ij}\) ganz allgemein die Wahrscheinlichkeit, dass ein System vom Zustand \(i\) in den Zustand \(j\) übergeht. Die Übergangsmatrix umfasst alle möglichen Zustände, die das System annehmen kann, die also im Zustandsraum liegen. 

Zusätzlich ist die Übergangsmatrix stochastisch, was wiederum bedeutet, dass sich alle Einträge der Matrix in einer Zeile auf eins summieren, sodass das System sicher nach jedem Schritt in einen neuen Zustand übergeht oder im aktuellen Zustand verbleibt. Mathematisch wird diese Tatsache wie folgt ausgedrückt:

\(\) \[\sum_{j} p_{i,j} = 1 \]

Welche Eigenschaften besitzt eine Markov Kette?

Markov Ketten besitzen mehrere, wichtige Eigenschaften, die über das Verhalten und die Dynamik der Kette bestimmten. Im Folgenden werden einige Eigenschaften beschrieben, die eine Markov Kette annehmen kann, aber nicht muss. 

Irreduzibilität

Eine Markow Kette ist irreduzibel, wenn alle Übergangswahrscheinlichkeit echt positiv sind, also nicht null und auch nicht negativ sind. Diese Eigenschaft bedeutet, dass es möglich ist von jedem Zustand im System möglich ist, einen anderen Zustand zu erreichen. Das Gangschaltungsbeispiel wird erst dann irreduzibel, wenn man es erlaubt Gänge zu überspringen und somit direkt vom Rückwärtsgang in den sechsten Gang geschalten werden kann. 

Periodizität

Ein Zustand ist periodisch, wenn es nur möglich ist den Zustand nach einer Periode von \(d\) Schritten wieder zu erreichen ist. Obwohl das System weiterhin stochastisch bleibt, ist dadurch ein gewisser Determinismus vorhanden. Bei Monopoly beispielsweise äußert sich die periodische Eigenschaft dadurch, dass man vom Startpunkt zwar wieder auf den Startpunkt zurückkehren kann, dafür jedoch eine gewisse Mindestanzahl an Spielzügen erforderlich ist, da man einmal das gesamte Feld umwandern muss. 

Stationäre Verteilung

Eine Markow Kette folgt einer stationären Verteilung genau dann, wenn es eine Startverteilung gibt, die sich im Laufe des Systems nicht verändert und somit stationär bleibt. Mathematisch gesehen wird diese Verteilung durch \(\pi\) beschrieben. Diese besitzt die Eigenschaft, dass wenn \(\pi\) mit der Übergangsmatrix \(P\) multipliziert wird, wieder die Verteilung \(\pi\) herauskommt: 

\(\) \[\pi \cdot P = \pi \]

Durch Lösung dieser Gleichung findet man die stationäre Verteilung und eine feste Wahrscheinlichkeit für jeden Übergang. 

Rekkurenz und Transzienz

Diese Eigenschaften drehen sich um das Langzeitverhalten von Markow Ketten und beschreiben, wie oft gewisse Zustände erreicht werden. Wenn im Langzeitverhalten ein Zustand fast unendlich oft besucht wird, dann bezeichnet man ihn als rekurrent. Ansonsten heißt er transient. Wenn alle Zustände in einem Zustandsraum rekurrent sind, dann bezeichnet man die gesamte Markow Kette als rekurrent. 

Wie sieht das langfristige Verhalten von Markov Ketten aus?

Im Mittelpunkt der Analyse von Markov Ketten steht, wie sich das System langfristig verhält und ob es einen Zustand gibt, zu dem das System hin konvergiert und wie die Wahrscheinlichkeiten dann in diesem Gleichgewicht aussehen. Zentral für die Analyse des langfristigen Verhaltens ist der Gleichgewichtszustand und absorbierende Zustände. 

Ein zentraler Aspekt bei Markow Ketten ist der Gleichgewichtszustand oder die stationäre Verteilung. Unter bestimmten Umständen konvergiert die Markow Kette nach ausreichend Schritten hin zu dieser Verteilung. Die stationäre Verteilung ist die Verteilung, die multipliziert mit der Übergangsmatrix wieder die Verteilung ergibt. 

Beim Monopoly beispielsweise tendiert das System langfristig zu einer stationären Verteilung, die beschreibt, wie oft die Spieler auf den verschiedenen Feldern waren. Hierbei hat dann das Gefängnisfeld oder das Startfeld eine höhere Wahrscheinlichkeit als die übrigen Felder, da es mehrere Möglichkeiten gibt auf diese Felder zu gelangen. 

Eine weitere wichtige Beobachtung beim Langzeitverhalten von Markow Ketten ist, ob es zu sogenannten absorbierenden Zuständen kommt. Diese Zustände sind erreicht, wenn das System nicht mehr in der Lage ist, diesen Zustand zu verlassen und deshalb dort verbleibt. Im Glücksspiel ist beispielsweise der absorbierende Zustand erreicht, wenn ein Spieler kein Geld mehr besitzt und somit nicht mehr am Glücksspiel teilnehmen kann. 

Welche speziellen Arten von Markov Ketten gibt es?

Die Markow Ketten sind allgemeine stochastische Modelle, mit denen sich bereits viele reale Prozesse simulieren lassen. Jedoch gibt es auch Anwendungen, die sich mit den bisher vorgestellten Eigenschaften nicht vereinbaren lassen. Deshalb haben sich über die Zeit hinweg verschiedene spezielle Markow Ketten entwickelt. 

Mithilfe von Geburten- und Todesprozesse werden kontinuierliche Markow Ketten beschrieben, die Zustandsveränderungen durch diskrete Ereignisse erfahren. In dem Prozess wird dadurch modelliert, wie Individuen in dem System plötzlich auftauchen oder verschwinden. Diese können beispielsweise bei einem Onlineshop verwendet werden, wenn neue Nutzer erscheinen oder den Webshop wieder verlassen. Die Übergangswahrscheinlichkeiten beschreiben dann die Häufigkeit, dass solche Geburts- oder Todesprozesse stattfinden. 

Bei reversiblen Markow Ketten ist nicht ersichtlich, ob der Prozess vorwärts oder rückwärts abläuft. Der Prozess kann somit umgekehrt werden, ohne dass sich die Übergangswahrscheinlichkeiten verändern. Einfach gesprochen bedeutet dies, dass die Wahrscheinlichkeit von Zustand \(i\) in den Zustand \(j\) überzugehen genauso hoch ist, wie vom Zustand \(j\) in den Zustand \(i\) überzugehen. 

Diese speziellen Ketten finden vor allem in der Physik und in der Chemie Anwendung, bei der Modellierung von Gleichgewichtssystemen. Durch die mathematischen Eigenschaften können hierbei rechnerische Vereinfachungen vorgenommen werden. 

Wie kann eine Markov Kette simuliert und in Python umgesetzt werden?

In der praktischen Anwendung und Analyse ist vor allem die Simulation von Markow Ketten interessant, um die langfristigen Eigenschaften und das Verhalten dieser Systeme zu untersuchen und Rückschlüsse auf die Realität zu ziehen. Markow Ketten werden in unterschiedlichen Bereichen, wie beispielsweise den Naturwissenschaften oder der Finanzmathematik angewendet. 

Eine weit verbreitete Möglichkeit hierfür ist die sogenannte Monte Carlo Simulation. Dabei werden wiederholt zufällige Zustandsfolgen erzeugt und damit die statistischen Eigenschaften der Kette geschätzt. Im Allgemeinen werden dabei diese Schritte wiederholt:

1. Initialisierung: Als erstes wird ein Startzustand ausgewählt, von dem aus das System beginnt. 
2. Übergang: Mithilfe der Übergangswahrscheinlichkeiten wird der nächste Zustand im System bestimmt. 
3. Wiederholung: Der Schritt 2 wird einige Male wiederholt, um einen längerfristigen Zeitraum zu simulieren.
4. Statistische Analyse: Nach dieser Zeit kann die Häufigkeit der Zustände betrachtet werden, um damit die stationäre Verteilung oder andere Eigenschaften der Markow Kette abschätzen zu können. 

Mithilfe von dieser Herangehensweise kann eine schnelle und einfache Analyse der Markow Kette stattfinden, ohne dass eine analytische Lösung der Übergangsgleichungen erforderlich ist. 

Um diese Herangehensweise in Python zu veranschaulichen, nutzen wir eine fiktive Markow Kette mit insgesamt drei Zuständen. Die Übergangswahrscheinlichkeiten definieren wir dabei so, dass die Wahrscheinlichkeit von einem Zustand in den anderen zu wechseln bei 50 % liegt. Damit die Wahrscheinlichkeiten in einer Zeile der Übergangsmatrix bei 100 % liegen, ist die Wahrscheinlichkeit, dass die Markow Kette im selben Zustand verbleibt bei 0 %. In Python kann diese Übergangsmatrix mithilfe eines NumPy Arrays erstellt werden. 

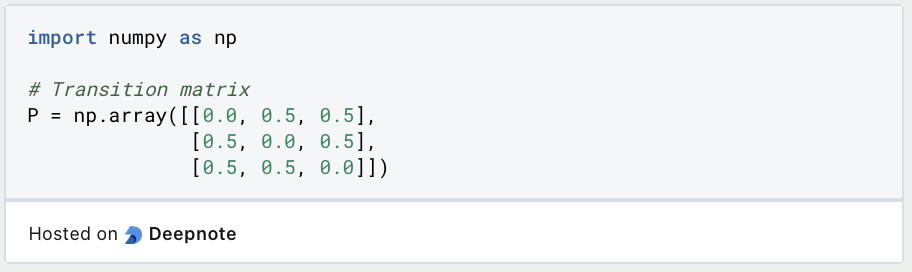
Als nächstes wird das System initialisiert und der Initialzustand festgelegt. Außerdem wiederholen wir die Monte Carlo Simulation 10.000-mal. 

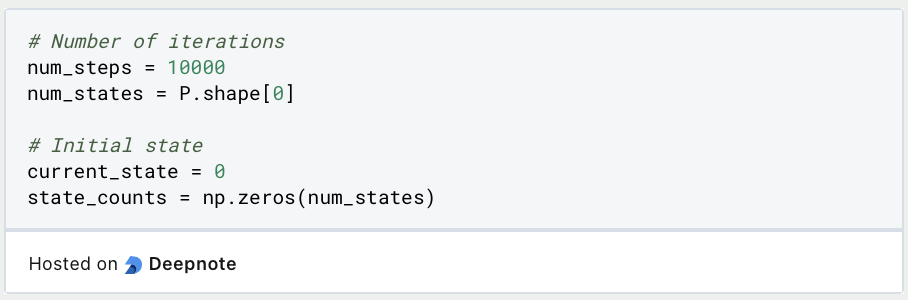
Während der Simulation wird in jedem Schritt zufällig einer der drei Zustände gewählt zu dem dann vorgerückt wird. Dabei werden die Wahrscheinlichkeiten aus der Übergangsmatrix berücksichtigt.

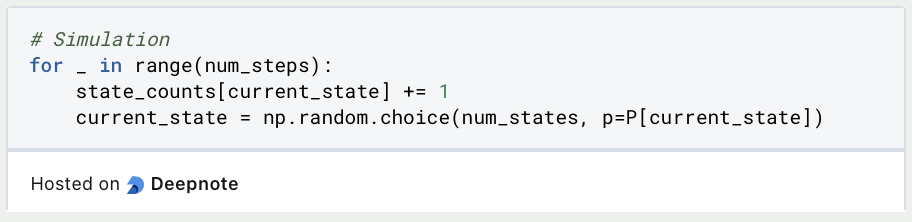
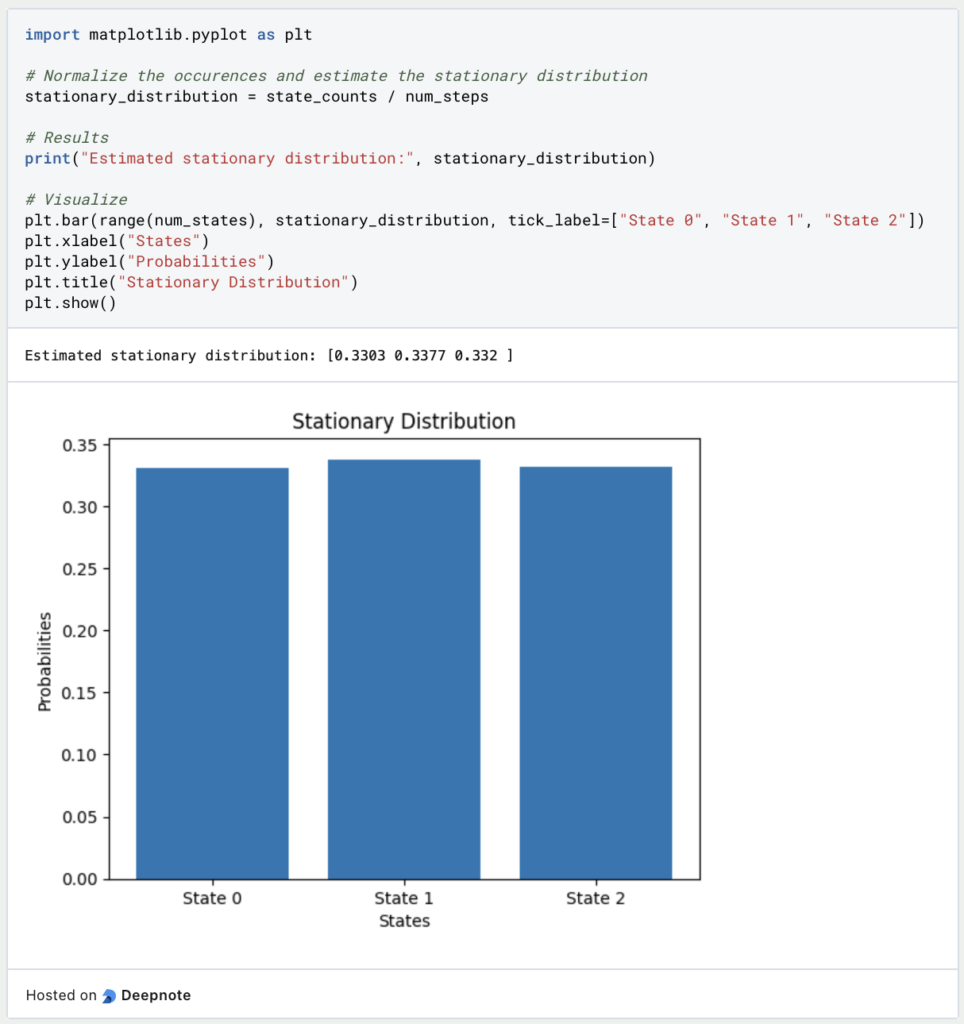
Abschließend können wir nun die stationäre Verteilung berechnen und diese mithilfe von Matplotlib grafisch ausgeben. Wie zu erwarten war, sind die drei Zustände nahezu gleich wahrscheinlich. Mithilfe von mehr Wiederholungen würde sich dieses Bild noch weiter verfestigen: 

Das solltest Du mitnehmen

• Markow Ketten sind stochastische Modelle, die Systeme von Zuständen beschreiben und wie diese sich über einen Zeitraum verhalten. 
• Für diese Ketten gilt die Markov Eigenschaft, die besagt, dass die Wahrscheinlichkeit des nächsten Zustands einzig vom aktuellen Zustand des Systems abhängt und nicht von der Vergangenheit. 
• Abhängig von der Zeitdefinition gibt es kontinuierliche und diskrete Markow Ketten. 
• Markow Ketten können unterschiedliche Eigenschaften besitzen, wie beispielsweise Periodizität oder die Rekurrenz. 
• Um Markow Ketten zu simulieren wird häufig die sogenannte Monte Carlo Simulation verwendet, die sich auch einfach in Python umsetzen lässt. 

Andere Beiträge zum Thema Markow Ketten

Die Universität Ulm hat ein Skript über Markov-Ketten, das Sie hier finden können.