Die Normalverteilung, oder auch Gauß-Verteilung, ist die wichtigste stetige Wahrscheinlichkeitsverteilung, da nahezu alle Werte, die wir in unserem Umfeld haben, normalverteilt sind. Körpergröße (innerhalb eines Geschlechts), die 100m Zeiten eines Schwimmers bei verschiedenen Wettkämpfen aber auch so etwas spezielles wie das Gewicht von mehreren Kaffeepackungen folgen ab einer ausreichend großen Stichprobe der Gauß-Verteilung. 

Wenn wir ein Zufallsexperiment durchführen, wie beispielsweise die Zeiten eines Schwimmers immer wieder messen, dann wollen wir zum einen eine sogenannte Dichtefunktion erhalten. Diese gibt uns an wie häufig ein gewisses Ereignis vorkommt. Es könnte uns zum Beispiel interessieren, wie wahrscheinlich es ist, dass der Schwimmer die 100m in einer Zeit von 1:15 min vollendet. Zusätzlich könnte uns aber auch interessieren, wie hoch die Wahrscheinlichkeit ist, dass der Sportler die 100m in unter oder maximal 1:15min schwimmt. Diese Frage können wir mit hilfe der Verteilungsfunktion beantworten. Die Verteilungsfunktion gibt an mit welcher Wahrscheinlichkeit das Ergebnis des Zufallsexperiment kleiner oder gleich eines bestimmten Wertes ist. 

Wie ist die Definition der Normalverteilung?

Eine stetige Zufallsgröße X mit einer Dichtefunktion f(x) der Form

\(\) \[f(x) = \frac{1}{\sigma \sqrt{2 \pi}} \cdot e^{-\frac{1}{2} \cdot \frac{(x – \mu)^2}{\sigma}}\]

mit dem Erwartungswert µ und der Varianz σ² heißt normalverteilt (kurz: N(µ, σ²)). Der Erwartungswert µ…

• … ist eine reelle Zahl, er kann also auch negativ werden.
• … ist die X-Koordinate des Maximums der Dichtefunktion.

Die Varianz σ²…

• … ist die quadrierte Standardabweichung σ. 
• … muss immer größer 0 sein.
• … bestimmt wie stark der Graph horizontal gestreckt oder gestaucht ist. Eine geringe Varianz bedeutet, dass der Graph schmal ist. 

Was ist die Dichtefunktion?

Im Zusammenhang mit der Normalverteilung, wird meistens die Dichtefunktion mit ihrer bekannten Glockenkurve gezeigt. Kurz gesagt nutzt man diesen Graphen, um für einen Erwartungswert X die Wahrscheinlichkeit abzulesen, mit der dieses Ereignis eintritt.

Der Graph bildet die Normalverteilung von Körpergrößen in Zentimetern ab, die bei männlichen Testpersonen gemessen wurden. Der Erwartungswert µ = 180 sagt aus, dass der Großteil der Probanden 180cm groß waren. Die Varianz σ² beträgt in diesem Beispiel 7. Die Wahrscheinlichkeit für den Erwartungswert X = 176 beträgt etwa 5%, d.h. eine zufällige, männliche Testperson ist mit einer Wahrscheinlichkeit von 5% genau 176cm groß.

Was ist die Verteilungsfunktion?

Die Verteilungsfunktion F(x) der Normalverteilung ist definiert durch

\(\) \[f(x) = \frac{1}{\sigma \sqrt{2 \pi}} \cdot \int_{- \infty}^{x} e^{-\frac{1}{2} \cdot \frac{(x – \mu)^2}{\sigma}} \]

Also das Integral der Dichtefunktion f(x) im Bereich von – bis zur Zufallsgröße X. Die Verteilungsfunktion gibt entsprechend an, wie hoch die Wahrscheinlichkeit ist, dass die Zufallsgröße einen Wert von kleiner oder gleich X annimmt: 

\(\) \[ f(x) = Prob(X \leq x) \]

Für den Erwartungswert X = 176 erhalten wir in der Verteilungsfunktion eine Wahrscheinlichkeit von etwa 6,7%. Eine zufällige, männliche Person ist somit mit einer Wahrscheinlichkeit von 6,7% kleiner oder genau 176cm groß. 

Was ist die empirische Regel der Normalverteilung?

Die empirische Regel, auch bekannt als 68-95-99,7-Regel, ist eine statistische Richtlinie für die Normalverteilung. Sie besagt, dass:

• Ungefähr 68 % der Daten liegen innerhalb einer Standardabweichung des Mittelwerts.
• Ungefähr 95 % der Daten liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
• Ungefähr 99,7 % der Daten liegen innerhalb von drei Standardabweichungen vom Mittelwert.

Diese Regel kann beim Interpretieren und Verstehen von Daten, die einer Normalverteilung folgen, hilfreich sein. Wenn wir zum Beispiel wissen, dass ein Datensatz normalverteilt ist, und wir seinen Mittelwert und seine Standardabweichung berechnen, können wir die empirische Regel verwenden, um den Anteil der Daten zu schätzen, der in bestimmte Bereiche fällt.

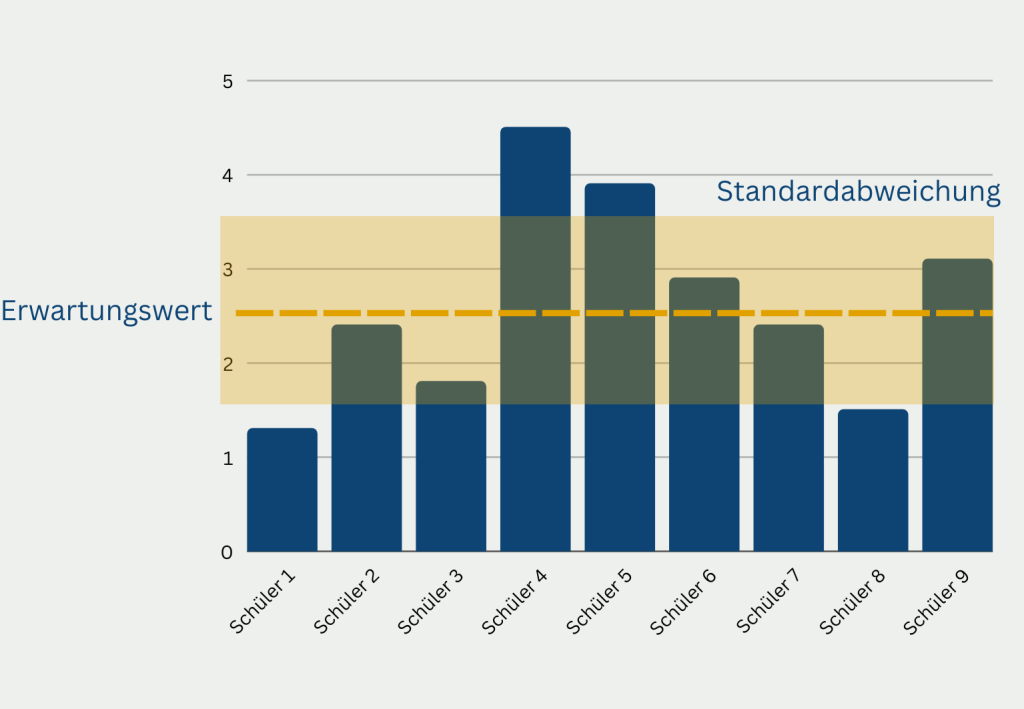
Es ist wichtig zu beachten, dass die empirische Regel nur eine Annäherung ist und nicht für alle Normalverteilungen gilt. Außerdem gilt sie nur für kontinuierliche Daten, die einer Normalverteilung folgen, und nicht für kategoriale oder diskrete Daten. Nichtsdestotrotz kann die empirische Regel ein nützliches Instrument sein, um Einblicke in normalverteilte Daten zu gewinnen.

Welche Alternativen zur Normalverteilung gibt es?

Für viele Anwendungen eignet sich die Normalverteilung sehr gut, um kontinuierliche Zufallsvariablen in der Statistik zu modellieren. In einzelnen Situationen sind jedoch andere Verteilungen geeigneter. Die bekanntesten Alternativen sind:

• Die Binomialverteilung wird verwendet, um Situationen mit einem binären Ergebnis, zum Beispiel Kopf oder Zahl, zu modellieren. Hierfür wird die Anzahl der Erfolge bei einer festen Anzahl an versuchen gemessen.
• Die Poisson-Verteilung dient zur Abbildung von Ereignissen, die in einem festen Zeit- oder Raumintervall auftreten. Hierbei ist wichtig zu beachten, dass zwei Ereignisse nicht gleichzeitig stattfinden können und dass die Einzelereignisse unabhängig voneinander sind.
• Die Exponentialverteilung ist eng mit der Poisson-Verteilung verbunden und modelliert die Zeit zwischen zwei aufeinanderfolgenden Ereignissen. In der Praxis kann dies beispielsweise die Dauer zwischen zwei Erdbeben sein oder die Zeit zwischen zwei Kunden, die ein Geschäft betreten.
• Die Gamma-Verteilung umfasst verschiedene Verteilungen, wie darunter auch die Exponentialverteilung als Spezialfall. Diese Verteilungen dienen zur Modellierung der Zeiten zwischen zwei Ereignissen ganz Allgemein.
• Die Beta-Verteilung wird genutzt, um eine Situation nachzustellen in der die Wahrscheinlichkeiten in einem begrenzten Bereich liegen. Also zum Beispiel den Anteil der Wähler, die für einen bestimmten Kandidaten stimmen.
• Die Weibull-Verteilung beschreibt die Zeit bis zum Ausfall eines System. Die Ausfallrate nimmt dabei mi der Zeit steig zu oder ab, wie beispielsweise die Wahrscheinlichkeit eines Reifenplatzers mit mehr gefahrenen Kilometern zunimmt.
• Die Gleichverteilung wird genutzt, um Zufallsvariablen mit konstanten Dichtefunktionen über einen bestimmten, endlichen Bereich abzubilden.

Jede Anwendung sollte auf eine geeignete Wahrscheinlichkeitsverteilung zurückgreifen, die auf der Art der Daten und der jeweiligen Forschungsfrage beruht. Die Ergebnisse hängen maßgeblich von der richtigen Wahl der Verteilung ab. Deshalb beschäftigen wir uns im nächsten Kapitel mit der Wahl der passenden Wahrscheinlichkeitsverteilung.

Wie wählt man die passende Datenverteilung?

Bei der Arbeit mit Daten ist es wichtig, die richtige Verteilung für den jeweiligen Datensatz zu wählen. Die Wahl der falschen Verteilung kann zu falschen Annahmen über die Daten führen und die Ergebnisse der durchgeführten Analyse oder Modellierung beeinträchtigen.

Eine Möglichkeit, die richtige Verteilung zu wählen, besteht darin, die Merkmale der Daten zu untersuchen. Wenn die Daten beispielsweise einen einzigen Spitzenwert oder Modus aufweisen, kann es angemessen sein, eine Normalverteilung anzunehmen. Wenn die Daten positiv schief sind, kann es sinnvoll sein, eine Lognormal- oder Gamma-Verteilung anzunehmen. Sind die Daten hingegen negativ geneigt, kann es sinnvoll sein, eine inverse Gamma- oder Weibull-Verteilung anzunehmen.

Ein anderer Ansatz ist die Verwendung statistischer Tests, um die Anpassung verschiedener Verteilungen an die Daten zu vergleichen. Zu den häufig verwendeten Tests gehören der Kolmogorov-Smirnov-Test, der Anderson-Darling-Test und der Chi-Quadrat-Test. Mit Hilfe dieser Tests lässt sich feststellen, welche Verteilung die beste Anpassung an die Daten bietet.

Es ist auch wichtig, den Kontext der Analyse oder Modellierung zu berücksichtigen. Wenn die Daten beispielsweise eine Anzahl von diskreten Ereignissen darstellen, kann es angemessen sein, eine Poisson- oder negative Binomialverteilung anzunehmen. Wenn die Daten einen Anteil darstellen, kann eine Beta-Verteilung angemessener sein.

Letztendlich erfordert die Wahl der richtigen Verteilung für die Daten eine sorgfältige Abwägung und ein Verständnis der Daten und des Kontexts, in dem sie verwendet werden sollen.

Was sind Hypothesentests und wie nutzen sie die Normalverteilung?

In der Statistik ist es häufig nicht praktikabel die komplette Gruppe an Objekten, die sogenannte Grundgesamtheit, zu befragen, um Rückschlüsse ziehen zu können. Dies ist meist aufgrund von zeitlichen oder monetären Beschränkungen nicht möglich. Deshalb wird versucht eine möglichst repräsentative Stichprobe zu bilden, mit deren Hilfe festgestellt werden kann, ob eine Hypothese, die in der Stichprobe beobachtet wird auch für die Grundgesamtheit zutrifft.

Da viele natürliche Phänomene, wie beispielsweise die Größe von Menschen, normalverteilt sind, nutzen Hypothesentests häufig eine Normalverteilung, um die Grundgesamtheit zu simulieren. Für die Hypothesenprüfung wird dann eine sogenannte Nullhypothese formuliert, die es zu testen gilt, wie zum Beispiel die Behauptung, dass höchstens zwei Prozent aller Teile in einer Produktion fehlerbehaftet sind. Um feststellen zu können, ob die Nullhypothese zutrifft oder nicht wird dann die Teststatistik, die abhängig von der angenommenen Verteilung ist, mit einem kritischen Wert verglichen. Dieser kritische Wert ist abhängig von dem sogenannten Signifikanzniveau, also einfach gesprochen, wie sicher man sich mit dem Ergebnis sein will.

Wenn die Teststatistik größer ist als der kritische Wert, wird die Nullhypothese verworfen und kann nicht auf die Grundgesamtheit übertragen werden. In unserem Fall würde dies bedeuten, dass nicht höchstens zwei Prozent der Produktionsteile fehlerhaft sind, was gleichbedeutend wäre mit der Aussage, dass mehr als zwei Prozent der Teile fehlerhaft sind.

Die Normalverteilung wird bei Hypothesentests genutzt, wenn angenommen wird, dass die Datenverteilung normalverteilt ist. Die Voraussetzung, dass die Hypothese in der Population normalverteilt ist, ermöglicht es uns entsprechende Rückschlüsse von der Verteilung in der Stichprobe auf die Verteilung in der Grundgesamtheit ziehen zu können. Dadurch kann beispielsweise die Standardabweichung der Grundgesamtheit geschätzt werden und außerdem kann die Wahrscheinlichkeit eines bestimmten Ereignisses oder eines Wertebereichs vorhergesagt werden.

Es ist jedoch wichtig zu beachten, dass nicht alle Phänomene normalverteilt sind. Wenn die Daten nicht normalverteilt sind, müssen wir bei der Hypothesenprüfung möglicherweise eine andere Verteilung verwenden. Es gibt viele verschiedene Wahrscheinlichkeitsverteilungen, jede mit ihren eigenen Eigenschaften und Anwendungen. Die Wahl der richtigen Verteilung für einen bestimmten Datensatz erfordert eine sorgfältige Prüfung der Art der Daten und der zu prüfenden Hypothese.

Das solltest Du mitnehmen

• Die Normalverteilung ist ein grundlegendes Konzept in der Statistik und Wahrscheinlichkeitstheorie.
• Sie wird häufig zur Modellierung verschiedener Phänomene in den Natur- und Sozialwissenschaften verwendet.
• Die empirische Regel bietet einen nützlichen Leitfaden für das Verständnis der Verteilung von Daten.
• Obwohl die Normalverteilung ein gängiges und nützliches Modell ist, ist es wichtig, gegebenenfalls auch alternative Verteilungen in Betracht zu ziehen.
• Die Wahl der richtigen Verteilung für die Daten ist für eine genaue statistische Analyse unerlässlich.
• Hypothesentests sind ein leistungsfähiges Instrument, das sich auf die Normalverteilung stützt, um Rückschlüsse auf Populationsparameter zu ziehen.
• Das Verständnis der Normalverteilung und ihrer Eigenschaften ist eine wichtige Grundlage für weitere Studien im Bereich Statistik und Datenanalyse.

Andere Beiträge zum Thema Normalverteilung

• Eine prägnante Zusammenfassung zu dem Thema findest Du hier.