Die Standardabweichung ist ein sogenanntes Streumaß, welches eine Aussage darüber trifft, wie weit die Datenpunkte in einem Datensatz vom Mittelwert entfernt liegen. In der Praxis wird der griechische Buchstabe σ (Sigma) als Symbol genutzt.

Was ist die Standardabweichung?

In der Statistik gibt es verschiedene Kennwerte, die einen Datensatz oder eine Verteilung von Werten genauer beschreiben. Häufig wird dafür beispielsweise der Erwartungswert herangezogen, der bei einer Wahrscheinlichkeitsverteilung den Wert ausgibt, der am wahrscheinlichsten eintreten wird.

\(\) \[E(X) = x_1 \cdot P(X = x_1) + x_2 \cdot P(X = x_2) + … + x_n * P(X = x_n)\]

Der Wert alleine reicht jedoch nicht aus, um detaillierte Informationen über einen Datensatz zu liefern. Angenommen wir wollen zwei Schulklassen vergleichen, die dieselbe Klausur geschrieben haben und nach der Bewertung, denselben Notendurchschnitt, also denselben Erwartungswert, von 2,5 erzielt haben. Würden wir nun annehmen, dass die Schüler beider Klassen in etwa dasselbe Wissen besitzen?

Wahrscheinlich nur dann, wenn die Schüler der beiden Klassen ähnliche Noten erzielt haben. In Klasse A kommt der Durchschnitt von 2,5 jedoch dadurch zustande, dass einige starke Schüler eine 1,0 geschrieben haben, während andere, schwächere Schüler in der Klausur nur eine 4,0 erzielen konnten. In Klasse B hingegen liegen die Schüler sehr viel enger beieinander und es wurden vor allem die Note 2 und die Note 3 erzielt. Ausreißer nach oben und unten gab es hingegen gar nicht.

In der Statistik nennt man diese Kennwerte das Streuungsmaß. Man schaut sich dabei an, wie weit die einzelnen Werte, in unserem Fall die Schüler, vom Erwartungswert, also dem Notendurchschnitt, entfernt sind. Zwei Datensätze können zwar denselben Erwartungswert haben, jedoch sehr unterschiedliche Streuungsmaße.

Was ist die Varianz und wie berechnet man sie?

Die Varianz ist ein Streuungsmaß aus der Statistik. Es berechnet die Summe der durchschnittlichen Abweichung der Datensätze vom Mittelwert und setzt diese Differenz ins Quadrat. Durch das Quadrat werden positive und negative Abweichungen vom Mittelwert mit einbezogen und können sich nicht gegenseitig aufheben. Außerdem fallen durch das Quadrieren große Abweichungen viel stärker ins Gewicht als kleine.

\(\) \[\sigma^2 = \sum_{i=1}^{n}(x_{i} – E(X)) \cdot p_{i}\]

Wer bis hierher aufgepasst hat stellt fest, dass die Varianz kein eigenes Symbol oder einen eigenen griechischen Buchstaben besitzt, sondern mit σ^2 gekennzeichnet wird. Wie wir bereits gesagt hatten, steht σ für die Standardabweichung. Somit ist die Varianz die quadrierte Standardabweichung.

Wie berechnet man die Standardabweichung?

Da wir nun bereits den Zusammenhang zwischen Varianz und Standardabweichung kennen, lässt sich die dazugehörige Formel ziemlich einfach aufstellen, da es sich lediglich um die Wurzel der Varianz handelt:

\(\) \[\sigma = \sqrt{\sigma^2} = \sqrt{\sum_{i=1}^{n}(x_{i} – E(X)) \cdot p_{i}}\]

Wie interpretiert man den Wert?

Wie wir bereits erklärt haben, macht es bei der Varianz durchaus Sinn, die Differenz aus dem Datenpunkt und dem Erwartungswert zu quadrieren. Jedoch ist die Varianz dadurch auch deutlich schwieriger zu interpretieren, da sie nicht wirklich praktikabel ist.

Bei der Standardabweichung ist das hingegen anders, da wir hier wieder die Wurzel ziehen und somit wieder in der ursprünglichen Einheit sind. Für unser Klausurbeispiel würde somit eine Standardabweichung von 1,2 bedeuten, dass die Klasse im Schnitt eine Note erzielt, die 1,2 über oder unter dem Notendurchschnitt von 2,5 liegt. Durch diesen Wert wird also ein Intervall von 1,3 bis 3,7 eröffnet, da die Richtung der Abweichung nicht angegeben ist.

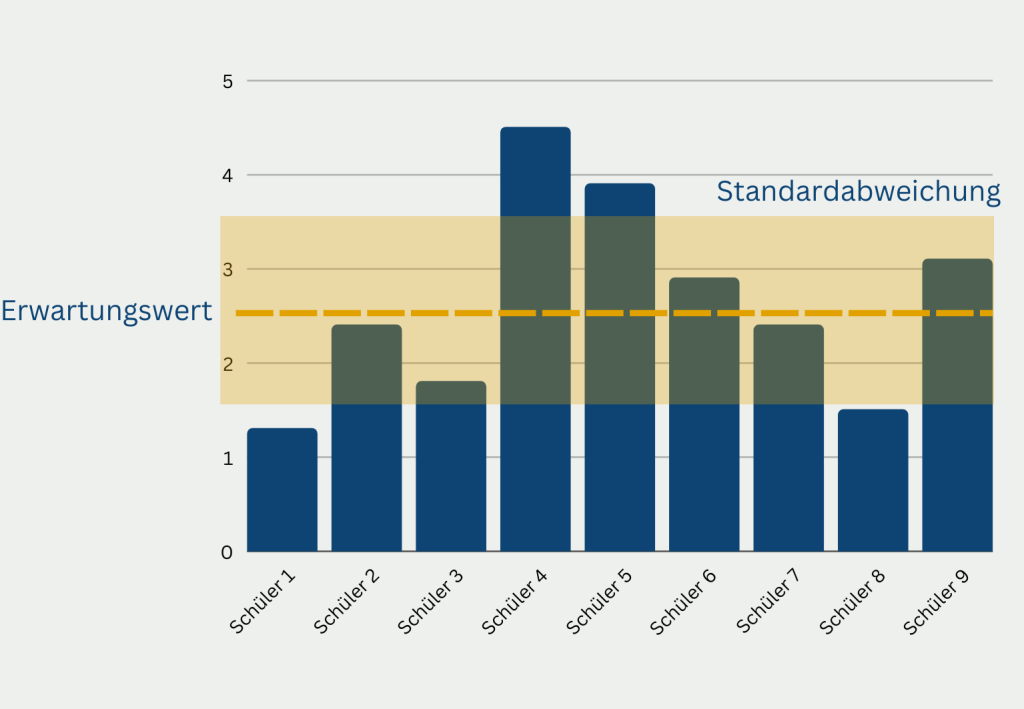
Eine niedrigere Standardabweichung bedeutet also allgemein, dass der Datensatz relativ nah am Erwartungswert gelegen ist und die einzelnen Datensätze nur sehr wenig von ihm abweichen.

Wann nutzt man die Standardabweichung für die Grundgesamtheit und wann für die Stichprobe?

In mancher Literatur werden zwei verschiedene Standardabweichungen unterschieden, nämlich für die Grundgesamtheit, die dann mit σ beschrieben wird, und die für die Stichprobe, welche mit s, gekennzeichnet wird. Die beiden Begriffe unterscheiden sich in der zugrundeliegenden Menge, die untersucht wurde:

• Die Untersuchungseinheit (auch Stichprobe oder Sample (engl.) genannt) sind einzelne Elemente aller Objekte (z.B. die Gesellschaft) von denen in einer Untersuchung Daten erhoben werden. Diese können dann für eine statistische Analyse genutzt werden. 
• Die Grundgesamtheit (Population (engl.) genannt) ist die Zusammenfassung aller Untersuchungseinheiten. Für diese Gruppe will man mithilfe der statistischen Analyse Aussagen treffen können. 

In der Statistik ist es eigentlich nicht möglich oder einfach nicht praktikabel die komplette Grundgesamtheit zu befragen. Deshalb wird versucht, eine möglichst repräsentative Untersuchungseinheit zu finden, die eine Verallgemeinerung auf die Grundgesamtheit zulässt.

In der Formel für die Standardabweichung unterscheiden sich die beiden Varianten lediglich dadurch, dass man für die Grundgesamtheit durch die Größe der Stichprobe teilt und für die Standardabweichung der Stichprobe lediglich durch die Größe der Stichprobe – 1 teilt.

Was ist die empirische Regel der Normalverteilung?

Die empirische Regel hilft bei der Interpretation der Normalverteilung und ist auch als 68-95-99,7 Regel bekannt. Sie besagt, dass:

• Innerhalb von einer Standardabweichung vom Mittelwert lassen sich bei einem normalverteilten Datensatz 68 % der Datenpunkte finden.
• Innerhalb von zwei Standardabweichungen vom Mittelwert lassen sich bei einem normalverteilten Datensatz etwa 95 % der Datenpunkte finden.
• Innerhalb von drei Standardabweichungen vom Mittelwert lassen sich bei einem normalverteilten Datensatz etwa 99,7 % der Datenpunkte finden.

Diese Regel ist eine wichtige Hilfe bei der Interpretation von Datensätzen, die einer Normalverteilung folgen oder von denen angenommen wird, dass sie einer Normalverteilung folgen. Wenn dann der Mittelwert und die Standardabweichung bekannt sind, können wichtige Schlüsse aus dem Datensatz gezogen werden, die hinreichend genau sind.

Jedoch hat die empirische Regel auch ihre Tücken, da sie das Vorliegen einer Normalverteilung voraussetzt und sonst nicht genutzt werden kann. Außerdem kann sie nicht für kategoriale oder diskrete Daten verwendet werden, da diese nicht normal verteilt sind, was jedoch in einigen Anwendungen gegeben ist. Trotz alledem ist die empirische Regel eine wichtige Stütze in der heutigen Statistik.

Was wird bei der Standardabweichung oft missverstanden?

Bei der Arbeit mit der Standardabweichung lassen sich viele oft von dem reinen Wert verleiten und treffen falsche Vorhersagen basierend auf dieser Kennzahl. Folgende Missverständnisse passieren häufig:

• Wahrheitsgehalt: Die Standardabweichung sagt nichts über die Genauigkeit oder die Präzision der Daten aus. Eine kleine Abweichung weist ebenso wenig auf genaue Daten hin, wie ein großer Wert auf fehlerhafte oder unzuverlässige Daten hinweist.
• Diese Kenngröße kann nicht nur bei der Auswertung von normal verteilten Daten verwendet werden, sondern lässt sich auch auf andere Datenverteilungen anwenden.
• Außerdem gibt es häufig Missverständnisse über die Standardabweichung der Grundgesamt und der Stichprobe. Hierbei sollte beachtet werden, wann die jeweiligen Kennzahlen zu verwenden sind und vor allem bedacht werden, dass diese unterschiedlich sind.

Solche Missverständnisse können schneller als gedacht auftreten. Deshalb ist es wichtig, die folgenden Regeln zu beachten, um diese falschen Interpretationen zu vermeiden:

• Eine geringe Standardabweichung besagt ausschließlich, dass die Datenpunkte sehr nahe am Mittelwert liegen, was keinen Rückschluss auf die Genauigkeit der Daten zulässt. Die Körpergröße beispielsweise hat eine geringe Standardabweichung, jedoch bedeutet dies nicht bei jedem Datensatz zur Körpergröße, dass dieser auch ausreichend genau ist.
• Bevor die Standardabweichung genutzt wird, sollte die zugrundeliegende Verteilung der Daten geprüft werden, um sicherzustellen, dass die Kennzahl richtig eingesetzt wird. Außerdem sollte man, nur weil keine Normalverteilung vorliegt, nicht automatisch die Standardabweichung außen vor lassen.
• Bei der Arbeit mit einer Stichprobe, sollte auch auf die Stichprobenstandardabweichung zurückgegriffen werden, um die entsprechende Kennzahl der Grundgesamtheit zu schätzen.

Wenn diese Missverständnisse bei der Arbeit mit Datensätzen beachtet werden, lassen sich viele einfache Fehler bei der Interpretation von Daten einfach vermeiden und es ist sichergestellt, dass die Standardabweichung korrekt verwendet wurden. Darauf basierende Schlussfolgerungen können wichtige Erkenntnisse über die Grundgesamtheit liefern.

Wie hängen Standardabweichung, Hypothesentests und Konfidenzintervalle zusammen?

Zum Einsatz kommt die Standardabweichung beispielsweise bei sogenannten Hypothesentests. Diese statistische Methode prüft mithilfe eines Datensatzes, ob eine Hypothese statistisch signifikant ist, sodass sich Erkenntnisse aus dem Datensatz auf eine Population übertragen lassen. Dabei kommen die sogenannten Konfidenzintervalle ins Spiel, die verwendet werden, um den Wertebereich zu finden, in dem der Populationsparameter voraussichtlich liegt.

Bei der Hypothesenprüfung kommen verschiedene Kennzahlen zum Einsatz, die unter anderem mithilfe der Standardabweichung berechnet werden können. Zum einen gibt es die sogenannte Teststatistik, die aus der Differenz zwischen Stichprobenmittelwert und dem hypothetischen Populationsmittelwert besteht. Diese Differenz wird dividiert durch den Standardfehler des Mittelwerts. Dieser wiederum ist die Standardabweichung der Stichprobenverteilung. Diese Teststatistik wird dann mit einem kritischen Wert verglichen, um festzustellen, ob Hypothese bestätigt werden kann oder nicht.

Dazu werden die sogenannten Konfidenzintervalle gebildet, die mithilfe des Stichprobenmittelwerts und dem Abweichungswert errechnet werden. Das Konfidenzintervall umfasst alle Werte, die um den Stichprobenmittelwert liegen plus oder minus einer Fehlermarge. Diese Marge erhält man durch die Multiplikation des Standardfehlers mit einem kritischen Wert, der sich auf Grundlage des gewünschten Konfidenzniveaus ergibt. Die Standardabweichung ist maßgeblich für die Breite des Konfidenzintervalls.

Mithilfe dieser Methode können Analysten belastbare Aussagen basierend auf Datensätzen liefern, die einen Einblick in die Gesamtpopulation und deren Zusammenhänge liefert. Die Standardabweichung ist dabei von entscheidender Bedeutung, um ein besseres Verständnis für die Variabilität der Daten zu bekommen und dadurch genauere Vorhersagen und Schlussfolgerungen zu treffen.

Das solltest Du mitnehmen

• Die Standardabweichung ist ein sogenanntes Streuungsmaß aus der Statistik.
• Es gibt Auskunft darüber, wie weit die einzelnen Datenpunkte im Schnitt vom Erwartungswert entfernt sind. Eine niedrige Standardabweichung sagt aus, dass die Datenpunkte relativ nahe am Erwartungswert gelegen sind und vice versa.
• Die Standardabweichung ist eng verwandt mit der Varianz, da sie lediglich die Quadratwurzel der Varianz ist.

Andere Beiträge zum Thema Standardabweichung

Statista bietet einen ausführlichen Beitrag zum Thema.