Im Bereich der Statistik und der Regressionsmodellierung sind Präzision und Zuverlässigkeit von größter Bedeutung. Stelle Dir vor, Du hättest ein Werkzeug, das verborgene Probleme in Deinen Modellen aufdeckt und so die Vertrauenswürdigkeit Deiner Erkenntnisse erhöht. Dieses Werkzeug ist als Varianzinflationsfaktor, kurz VIF, bekannt. In diesem Artikel werden wir die Bedeutung dieses Maßes bei der Erkennung von Multikollinearität untersuchen, einem häufigen, aber oft übersehenen Problem bei der Regressionsanalyse. Tauche mit uns in die Welt des VIF ein, entschlüssel seine Funktionsweise und erfahre, wie er die Qualität Deiner datengestützten Entscheidungen verbessern kann.

Was ist Multikollinearität?

In der Welt der Regressionsanalyse besteht eine der wichtigsten Annahmen darin, dass die Prädiktorvariablen (auch als unabhängige Variablen bezeichnet) voneinander unabhängig sein sollten. Das bedeutet, dass Veränderungen bei einem Prädiktor keinen signifikanten Einfluss auf Veränderungen bei einem anderen haben sollten. Die Multikollinearität stellt diese Annahme jedoch in Frage.

Multikollinearität bezieht sich auf eine Situation, in der zwei oder mehr Prädiktorvariablen in einem Regressionsmodell hoch korreliert sind. Einfacher ausgedrückt, handelt es sich um zwei oder mehr Merkmale, die so miteinander verflochten sind, dass es schwierig wird, ihre individuellen Auswirkungen auf die abhängige Variable zu entschlüsseln.

Stelle Dir vor, Du versuchst, Hauspreise vorherzusagen, und Du nimmst sowohl die Anzahl der Schlafzimmer als auch die Gesamtfläche eines Hauses als Vorhersagevariablen auf. Es ist wahrscheinlich, dass diese beiden Merkmale korreliert sind, da größere Häuser in der Regel mehr Schlafzimmer haben. Wenn Multikollinearität vorliegt, wird es schwierig, die spezifischen Auswirkungen der einzelnen Merkmale auf das Ergebnis zu erkennen, was zu unzuverlässigen und instabilen Regressionsergebnissen führen kann.

Multikollinearität ist nicht nur auf zwei Variablen beschränkt, sondern kann auch mehrere Prädiktoren in einem Modell betreffen. Dieses Phänomen kann die wahren Beziehungen zwischen den Prädiktoren und der Antwortvariablen verschleiern, was es schwierig macht, aussagekräftige Schlussfolgerungen zu ziehen und die Interpretierbarkeit des Regressionsmodells zu untergraben.

Das Verständnis der Multikollinearität ist bei der Regressionsanalyse von entscheidender Bedeutung, da sie zu Mehrdeutigkeit und Unsicherheit in den Vorhersagen Ihres Modells führen kann. Die Identifizierung und Behebung von Multikollinearität ist von entscheidender Bedeutung, um die Zuverlässigkeit und Genauigkeit Ihrer Regressionsergebnisse zu gewährleisten.

Was ist der Varianzinflationsfaktor?

Der Varianzinflationsfaktor ist ein statistisches Maß zur Bewertung des Ausmaßes der Multikollinearität in einer Regressionsanalyse. Er gibt an, wie stark die Varianz eines geschätzten Regressionskoeffizienten zunimmt, wenn die Prädiktoren korreliert sind. Im Wesentlichen hilft er Dir festzustellen, wie stark die Standardfehler der Regressionskoeffizienten aufgrund von Multikollinearität aufgebläht sind.

Und so funktioniert es:

Bei einem multiplen linearen Regressionsmodell mit mehreren Prädiktorvariablen wird jede Koeffizientenschätzung unter Kontrolle des Einflusses der anderen Prädiktoren berechnet. Wenn diese Prädiktoren korreliert sind, werden die Koeffizientenschätzungen instabil, was zu größeren Standardfehlern führt. Der VIF misst das Ausmaß dieser Instabilität.

Mathematisch gesehen wird der VIF für eine bestimmte Prädiktorvariable als das Verhältnis der Varianz der Koeffizientenschätzung bei Einbeziehung aller Prädiktoren zur Varianz der Koeffizientenschätzung bei Ausschluss dieses bestimmten Prädiktors aus dem Modell berechnet. Die Formel lautet wie folgt:

\(\) \[VIF = \frac{1}{(1 – R^2)} \]

Wobei:

• R² ist das Bestimmtheitsmaß der Prädiktorvariable in einem Regressionsmodell, das alle anderen Prädiktorvariablen als Prädiktoren verwendet.

Der VIF-Wert liefert wertvolle Erkenntnisse:

• Ist der VIF-Wert gleich 1, bedeutet dies, dass keine Multikollinearität vorliegt; die Prädiktorvariable ist nicht mit anderen Prädiktorvariablen korreliert.
• Ist der Wert größer als 1, aber kleiner als 5, deutet dies auf eine mäßige Multikollinearität hin, die nicht unbedingt ein großes Problem darstellt.
• Wenn der VIF-Wert 5 oder 10 übersteigt, deutet dies auf eine hohe Multikollinearität hin, was bedeutet, dass die Prädiktorvariable stark mit anderen Variablen im Modell korreliert ist. Hohe VIF-Werte können zu instabilen Koeffizientenschätzungen und unzuverlässigen p-Werten führen, was es schwierig macht, sinnvolle Schlussfolgerungen aus der Regressionsanalyse zu ziehen.

Analysten verwenden in der Regel VIF-Werte, um festzustellen, welche Prädiktorvariablen am stärksten zur Multikollinearität beitragen. Durch das Entfernen oder Ansprechen dieser Variablen oder durch andere Korrekturmaßnahmen wie die Auswahl von Merkmalen können die Auswirkungen der Multikollinearität abgeschwächt werden, was zu stabileren und zuverlässigeren Regressionsmodellen führt.

Wie kannst Du die VIF-Werte interpretieren?

Der Varianzinflationsfaktor ist ein wichtiges Instrument zur Bewertung der Multikollinearität in Regressionsmodellen. VIF-Werte geben Aufschluss darüber, inwieweit die Prädiktorvariablen miteinander korreliert sind. Die Interpretation von VIF-Werten ist wichtig, um fundierte Entscheidungen darüber zu treffen, ob und wie Multikollinearität behandelt werden soll.

Im Folgenden wird erläutert, wie VIF-Werte zu interpretieren sind:

• VIF = 1: Ein Wert von 1 bedeutet keine Multikollinearität. In diesem Fall ist die Prädiktorvariable nicht mit anderen Prädiktoren im Modell korreliert. Dieses Szenario ist ideal, weil es bedeutet, dass jeder Prädiktor einzigartige Informationen über die abhängige Variable liefert.
• VIF < 5: Werte unter 5 deuten im Allgemeinen darauf hin, dass die Multikollinearität zwischen den Prädiktorvariablen gering bis moderat ist. Auch wenn eine gewisse Korrelation besteht, ist sie in der Regel für die Regressionsanalyse nicht problematisch. Sie können mit dem Modell ohne größere Bedenken fortfahren.
• VIF ≥ 5: Ein VIF von 5 oder höher wird oft als rotes Tuch betrachtet, das auf erhebliche Multikollinearität hinweist. Dies bedeutet, dass die Prädiktorvariable stark mit einem oder mehreren anderen Prädiktoren im Modell korreliert ist. Hohe Werte können zu instabilen Koeffizientenschätzungen und einer verminderten Interpretierbarkeit des Regressionsmodells führen.
• VIF ≥ 10: Werte über 10 sind ein deutliches Zeichen für starke Multikollinearität. In solchen Fällen sind die Standardfehler der Regressionskoeffizienten erheblich aufgebläht, so dass es schwierig ist, den Koeffizientenschätzungen zu vertrauen. Hohe VIF-Werte können zu unzuverlässigen Vorhersagen führen und sollten behandelt werden.
• Analyse der spezifischen VIF-Werte: Während die Bewertung der Multikollinearität insgesamt wichtig ist, ist es auch sinnvoll, einzelne VIF-Werte zu untersuchen. Die Feststellung, welche spezifischen Prädiktorvariablen hohe Werte aufweisen, kann helfen, die Quellen der Multikollinearität im Modell zu ermitteln.

Bei der Interpretation von VIF-Werten ist ein Gleichgewicht zwischen statistischer Signifikanz und praktischer Bedeutung erforderlich:

• Eine geringe statistische Signifikanz (niedrige p-Werte) für Prädiktorvariablen kann darauf hindeuten, dass sie für das Modell wesentlich sind. In solchen Fällen kann es selbst bei mäßig hohen VIF-Werten (z. B. zwischen 5 und 10) akzeptabel sein, diese Variablen im Modell zu belassen, insbesondere wenn sie theoretisch relevant sind.
• Hohe VIF-Werte deuten zwar auf Multikollinearität hin, bedeuten aber nicht unbedingt, dass eine Variable aus dem Modell entfernt werden sollte. Dies hängt von der Forschungsfrage, dem Kontext und den mit der Modellvereinfachung verbundenen Kompromissen ab.

In der Praxis beinhaltet der Umgang mit Multikollinearität oft eine Kombination von Strategien, einschließlich der Entfernung stark korrelierter Variablen, der Kombination zu zusammengesetzten Variablen oder der Verwendung von Regularisierungstechniken wie Ridge-Regression. Die Wahl der Maßnahme sollte sich an den spezifischen Zielen der Analyse und den Auswirkungen auf die Interpretierbarkeit des Modells und die Vorhersageleistung orientieren.

Wie kann man Multikollinearität in Python entdecken?

Die Erkennung von Kollinearität in Deinem Datensatz ist ein entscheidender Schritt, bevor Du mit der statistischen Analyse fortfährst oder Vorhersagemodelle erstellst. Glücklicherweise gibt es mehrere Methoden und Techniken, um das Vorhandensein von Kollinearität zwischen Vorhersagevariablen festzustellen:

1. Korrelationsmatrix: Der gängigste Ansatz ist die Berechnung der Korrelationsmatrix aller Prädiktorvariablen. Korrelationskoeffizienten, wie z. B. der Korrelationskoeffizient von Pearson, quantifizieren die Stärke und Richtung der linearen Beziehungen zwischen Variablenpaaren. Hohe absolute Korrelationswerte (nahe bei 1 oder -1) zwischen zwei oder mehr Variablen deuten auf eine mögliche Kollinearität hin.

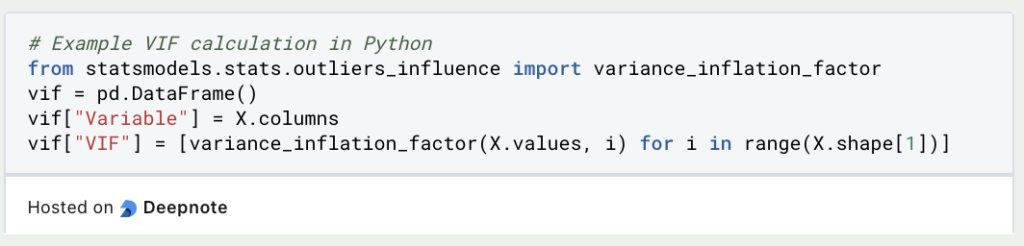
2. Varianzinflationsfaktor: Dieser misst das Ausmaß, in dem die Varianz der geschätzten Regressionskoeffizienten aufgrund von Kollinearität zunimmt. Ein hoher VIF (in der Regel über 5 oder 10) für eine Variable weist auf Probleme mit anderen Variablen hin.

3. Paarweise Streudiagramme: Die visuelle Inspektion von Streudiagrammen zwischen Variablenpaaren kann lineare Muster aufzeigen. Variablen, die starke lineare Trends aufweisen, wenn sie gegeneinander aufgetragen werden, können kollinear sein.

4. Eigenwerte der Korrelationsmatrix: Die Eigenwerte geben die Größe der Varianz in den Daten entlang bestimmter Dimensionen an. Kleine Eigenwerte (nahe Null) deuten darauf hin, dass einige Variablen stark korreliert sind, was auf Kollinearität hindeuten könnte.

5. Toleranz und Zustandsindex: Diese Metriken bieten zusätzliche Einblicke in die kollinearen Variablen. Die Toleranz misst den Anteil der Varianz in einer Variablen, der nicht durch andere Prädiktorvariablen erklärt wird, wobei eine niedrige Toleranz auf Kollinearität hinweist. Der Zustandsindex quantifiziert den Schweregrad der Multikollinearität; höhere Werte deuten auf stärker kollineare Variablen hin.

Sobald Du dieses Problem erkannt hast, kannst Du geeignete Schritte unternehmen, um es zu beheben. Dazu kann das Entfernen einer der korrelierten Variablen, die Transformation von Variablen oder die Verwendung von Regularisierungstechniken wie Ridge-Regression gehören. Die Erkennung ist ein wichtiger Teil der Datenvorbereitung.

Welche Maßnahmen helfen bei Multikollinearität?

Multikollinearität, ein häufiges Problem bei der Regressionsanalyse, kann die Zuverlässigkeit von Vorhersagemodellen beeinträchtigen. Glücklicherweise gibt es mehrere praktische Strategien, um ihre Auswirkungen abzuschwächen:

1. Redundante Variablen entfernen: Der erste Schritt im Umgang mit Multikollinearität besteht darin, hoch korrelierte Prädiktorvariablen zu identifizieren und zu eliminieren. Auf diese Weise kannst Du die informativsten Variablen in Deinem Modell beibehalten und gleichzeitig die Redundanz reduzieren.
2. Kombiniere oder transformiere Variablen: Anstatt korrelierte Prädiktoren zu verwerfen, kannst Du neue Variablen erstellen, indem Du sie kombinierst oder transformierst. Bei diesem Ansatz bleiben die wesentlichen Informationen erhalten, während die Multikollinearität reduziert wird.
3. Verwenden Sie die Hauptkomponentenanalyse (PCA): Die PCA ist ein Verfahren zur Dimensionalitätsreduktion, mit dem korrelierte Variablen in eine Reihe unkorrelierter Hauptkomponenten umgewandelt werden können. Diese Komponenten können dann als Prädiktoren in Ihrem Modell dienen.
4. Regularisierungstechniken verwenden: Regularisierungsmethoden wie Ridge-Regression und Lasso-Regression können helfen, Multikollinearität zu vermeiden. Sie fügen der Regressionsgleichung einen Strafterm hinzu, der extreme Parameterschätzungen verhindert und die Multikollinearität wirksam abschwächt.
5. Ziehe die Methode der partiellen kleinsten Quadrate (PLS) in Betracht: PLS ist eine Alternative zur PCA. Sie kombiniert Dimensionalitätsreduktion mit Regression und zielt darauf ab, die Kovarianz zwischen den Prädiktoren und der Zielvariablen zu maximieren und gleichzeitig die Multikollinearität zu berücksichtigen.

Ein effektiver Umgang mit Multikollinearität verbessert die Genauigkeit und Interpretierbarkeit von Regressionsmodellen. Die Wahl der Strategie sollte sich an den Merkmalen Deines Datensatzes, den Zielen Deiner Analyse und dem Kontext Deines Problems orientieren.

Was sind die praktischen Anwendungsfälle von VIF?

Der Varianzinflationsfaktor spielt eine zentrale Rolle in verschiedenen Anwendungen, die seinen Nutzen über seine primäre Funktion der Erkennung von Multikollinearität zwischen Prädiktorvariablen in der Regressionsanalyse hinaus erweitern. Im Folgenden gehen wir auf praktische Szenarien ein, in denen sich der VIF als unverzichtbar erweist:

• Identifizierung von Multikollinearität: Die wichtigste Anwendung des VIF ist seine Fähigkeit, Multikollinearität zu erkennen – ein Phänomen, bei dem Prädiktorvariablen in einem Regressionsmodell eine hohe Korrelation aufweisen. Hohe VIF-Werte weisen auf eine starke Interdependenz zwischen den Prädiktoren hin. Die Identifizierung von Multikollinearität ist von entscheidender Bedeutung, da sie die Fähigkeit des Modells beeinträchtigen kann, die individuellen Auswirkungen dieser korrelierten Variablen auf die Zielvariable zu unterscheiden.
• Informierte Modellauswahl: Der VIF dient als Leitfaden für die Auswahl von Variablen, die in Regressionsmodelle aufgenommen werden sollen. Durch die Untersuchung der Werte können Analysten datengestützte Entscheidungen über die Beibehaltung, den Ausschluss oder die Umwandlung von Variablen treffen. Dieser Prozess optimiert die Leistung des Modells, indem er Probleme, die sich aus der Multikollinearität ergeben, entschärft.
• Verbesserte Interpretation der Koeffizienten: Multikollinearität erschwert die Interpretation von Regressionskoeffizienten. VIF hilft bei der Erstellung stabiler und interpretierbarer Koeffizientenschätzungen. Dank dieser Klarheit können Analysten den Einfluss der einzelnen Prädiktoren auf die Zielvariable besser verstehen und kommunizieren.
• Verbesserte Modellleistung: Multikollinearität kann prädiktive Modelle ernsthaft beeinträchtigen. Durch die Beseitigung der Multikollinearität mittels VIF-gesteuerter Variablenauswahl oder -transformation können Analysten genauere Modelle mit verbesserter Vorhersageleistung entwickeln.
• Abschwächung der Überanpassung: Überanpassung ist ein häufiger Fallstrick bei der Modellierung, wenn ein Modell übermäßig gut zu den Trainingsdaten passt, was zu einer schlechten Generalisierung auf neue Daten führt. Multikollinearität verschlimmert die Überanpassung. VIF hilft bei der Abschwächung dieses Problems und stellt sicher, dass die Modelle effektiv verallgemeinert werden.

Der Varianzinflationsfaktor geht über seine Rolle als Multikollinearitäts-Detektor in der Regressionsanalyse hinaus. Seine Fähigkeit, Multikollinearität aufzudecken und abzuschwächen, erhöht die Robustheit und Interpretierbarkeit von Regressionsmodellen. Als grundlegender Wert für die datengestützte Entscheidungsfindung bietet die VIF Vorteile für verschiedene Branchen und Forschungsbereiche, da sie die Präzision und den Erkenntnisgewinn von Analysen bereichert.

Was sind die Grenzen des Varianzinflationsfaktors?

Der Varianzinflationsfaktor ist ein wertvolles Instrument zur Erkennung von Multikollinearität in der Regressionsanalyse. Es ist jedoch wichtig, seine Grenzen zu kennen, um ihn effektiv zu nutzen:

Der VIF konzentriert sich in erster Linie auf die Identifizierung von Multikollinearität, die auftritt, wenn unabhängige Variablen in einem Regressionsmodell hohe Korrelationen aufweisen. Andere Faktoren, die die Leistung des Modells beeinträchtigen können, wie z. B. die Verzerrung durch ausgelassene Variablen oder Endogenität, werden jedoch nicht berücksichtigt.

Eine weitere Einschränkung ist die Annahme linearer Beziehungen zwischen den Variablen. In Fällen, in denen nichtlineare Zusammenhänge bestehen, liefert VIF daher möglicherweise keine genaue Bewertung der Multikollinearität.

Außerdem können die VIF-Werte je nach Größe des Datensatzes erheblich schwanken. In kleineren Datensätzen kann dieses Maß auf Multikollinearität hinweisen, auch wenn seine praktischen Auswirkungen minimal sind.

Es ist wichtig zu beachten, dass hohe VIF-Werte zwar auf Multikollinearität hindeuten, die Ergebnisse des Modells aber nicht unbedingt ungültig machen. In einigen Fällen kann ein hoher Wert akzeptabel sein, wenn die Multikollinearität die Ziele der Analyse nicht wesentlich beeinträchtigt.

Außerdem befasst sich der VIF ausschließlich mit exogener Multikollinearität, bei der die Prädiktoren miteinander korrelieren. Er befasst sich nicht mit der Endogenität, bei der die abhängige Variable die Prädiktoren beeinflusst, was zu verzerrten Schätzungen führen kann.

Um den Varianz-Inflations-Faktor wirksam einzusetzen, ist es wichtig, diese Einschränkungen zu berücksichtigen und ergänzende Techniken und Fachwissen zu nutzen, um zuverlässige Regressionsmodelle zu erstellen.

Das solltest Du mitnehmen

• Der Varianzinflationsfaktor ist ein leistungsfähiges Instrument zur Ermittlung von Multikollinearität in der Regressionsanalyse.
• Der VIF hilft bei der Bewertung des Ausmaßes, in dem unabhängige Variablen in einem Regressionsmodell miteinander korreliert sind.
• Hohe Werte weisen auf potenzielle Multikollinearität hin, die zu instabilen und unzuverlässigen Regressionsergebnissen führen kann.
• Der Umgang mit Multikollinearität ist entscheidend für die Erstellung gültiger und interpretierbarer Regressionsmodelle.
• Durch die Berechnung des VIF für jede Prädiktorvariable können Analysten problematische Beziehungen zwischen den Variablen aufdecken.
• VIF-Werte über einem bestimmten Schwellenwert (in der Regel 5 oder 10) werden häufig als Anzeichen für eine hohe Multikollinearität angesehen.
• Zur Verringerung der Multikollinearität können Variablen entfernt, kombiniert oder zusätzliche Daten erhoben werden.
• Der VIF ist zwar ein wertvolles Instrument, hat aber auch seine Grenzen, da er sich auf lineare Beziehungen konzentriert und die Endogenität nicht berücksichtigen kann.
• Es ist wichtig, die Werte im Kontext der spezifischen Analyse zu interpretieren und bei Bedarf zusätzliche Techniken in Betracht zu ziehen.
• Insgesamt ist VIF eine wertvolle Ergänzung des Instrumentariums von Datenanalysten und Statistikern zur Verbesserung der Qualität und Zuverlässigkeit von Regressionsmodellen.

Andere Beiträge zum Thema Varianzinflationsfaktor

Hier findest Du eine Erklärung, wie Du den VIF in der Python-Bibliothek statsmodels berechnen kannst.