Die Principal Component Analysis (kurz: PCA, deutsch: Hauptkomponentenanalyse) verwendet man, wenn man die Anzahl der Variablen in einem großen Datensatz verringern will. Sie versucht nur die Variablen im Datensatz zu halten, die einen Großteil der Varianz erklären. Alle Features, die stark mit anderen Features korrelieren, werden entfernt.

Warum nutzen wir die Principal Component Analysis?

Verschiedene Algorithmen, wie beispielsweise die Lineare Regression haben Probleme, wenn der Datensatz Variablen hat, die miteinander korreliert sind, also voneinander abhängen. Um dieser Problematik aus dem Weg zu gehen, kann es Sinn machen, die Variablen aus dem Datensatz zu entfernen, die mit einer anderen Variablen korrelieren. Gleichzeitig aber sollen die Daten auch nicht ihren ursprünglichen Informationsgehalt verlieren bzw. so viel Information wie möglich behalten. Die Principal Component Analysis verspricht eben genau solche Variablen zu entfernen, die mit anderen korreliert sind und keinen großen Informationsverlust bedeuten.

Eine weitere Anwendung von PCA haben wir bei Clusteranalysen, wie beispielsweise dem k-Means Clustering, bei welchem wir die Anzahl der Cluster im Vorhinein definieren müssen. Die Dimensionalität des Datensatzes zu verringern hilft uns dabei, einen ersten Eindruck von den Informationen zu bekommen und beispielsweise abschätzen zu können, welches die wichtigsten Variablen sind und wie viele Cluster der Datensatz haben könnte. Wenn wir es beispielsweise schaffen, den Datensatz auf drei Dimensionen zu reduzieren, können wir die Datenpunkte in einem Diagramm visualisieren. Daraus lässt sich dann möglicherweise schon die Anzahl der Cluster ablesen.

Zusätzlich bieten große Datensätze mit vielen Variablen auch die Gefahr, dass das Modell overfitted. Das bedeutet einfach erklärt, dass das Modell sich im Training zu stark an die Trainingsdaten anpasst und dadurch nur schlechte Ergebnisse für neue, ungesehene Daten liefert. Daher kann es beispielsweise bei Neuronalen Netzwerken Sinn machen, das Modell erst mit den wichtigsten Variablen zu trainieren und dann Stück für Stück neue Variablen hinzuzunehmen, die möglicherweise die Performance des Modell weiter erhöhen ohne Overfitting. Auch hier ist die Principal Component Analysis ein wichtiges Werkzeug im Bereich des Machine Learnings.

Wie funktioniert die PCA Analyse?

Der Kerngedanke der Principal Component Analysis ist, dass möglicherweise mehrere Variablen in einem Datensatz dasselbe messen, also korreliert sind. Somit kann man die verschiedenen Dimensionen zu weniger sogenannten Hauptkomponenten zusammenfassen, ohne, dass die Aussagekraft des Datensatzes darunter leidet. Die Körpergröße beispielsweise weist eine hohe Korrelation mit der Schuhgröße auf, da große Menschen in vielen Fällen auch eine größere Schuhgrößere haben und andersrum. Wenn wir also die Schuhgröße als Variable aus unserem Datensatz streichen, nimmt der Informationsgehalt nicht wirklich ab.

Der Informationsgehalt eines Datensatzes wird in der Statistik durch die Varianz bestimmt. Diese gibt an, wie stark die Datenpunkte vom Mittelpunkt entfernt sind. Je kleiner die Varianz, desto näher liegen die Datenpunkte bei ihrem Mittelwert und andersrum. Eine kleine Varianz sagt somit aus, dass der Mittelwert bereits ein guter Schätzwert für den Datensatz ist.

Die PCA versucht im ersten Schritt die Variable zu finden, die die erklärte Varianz des Datensatzes maximiert. Anschließend werden schrittweise mehr Variablen hinzugefügt, die den verbleibenden Teil der Varianz erklären, denn in der Varianz, also der Abweichung vom Mittelwert, steckt die meiste Information. Diese sollte erhalten bleiben, wenn wir darauf basierend ein Modell trainieren wollen.

Dabei versucht die Principal Component Analysis im ersten Schritt eine Linie zu finden, die den Abstand zwischen ihr und den Datenpunkten so gut es geht minimiert. Diese Vorgehensweise ist dieselbe, wie bei der Linearen Regression. Die Linie ist also eine aufsummierte Kombination aller einzelnen Features des Datensatzes und bildet die erste Hauptkomponente.

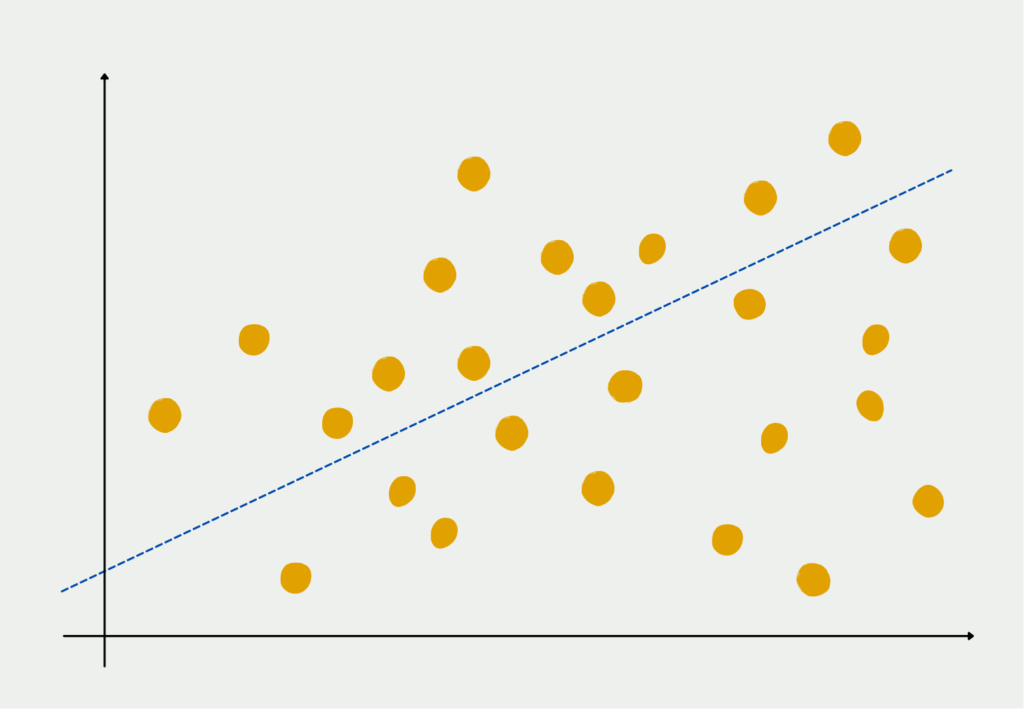
Anschließend wird versucht, eine zweite Linie zu erstellen, die orthogonal, also senkrecht, zur ersten Hauptkomponente steht und wiederum den Abstand zu den Datenpunkten minimiert. Die Linien müssen orthogonal zueinander stehen, da die Hauptkomponenten untereinander nicht korreliert sein sollen und weil eine senkrechte Linie auch sehr wahrscheinlich Varianz erklären kann, die in der ersten Komponente nicht enthalten ist.

Wie viele Hauptkomponenten sind das Ziel?

Grundsätzlich gibt es einen Zusammenhang zwischen der Anzahl der Hauptkomponenten und dem verbleibenden Informationsgehalt. Das bedeutet, dass man mit mehr Komponenten auch noch mehr Varianz erklären und somit Informationsgehalt im Datensatz hat. Sehr wenige Komponenten hingegen bedeuten, dass die Dimensionen stark verringert wurden, was der Zweck der Principal Component Analyse ist. Wir benötigen also mehr Komponenten, um den Inforamtionsgehalt zu erhöhen, jedoch nimmt dadurch der Effekt der PCA ab.

Nach Kaiser (1960) gibt es jedoch einen ganz guten Anhaltspunkt, nach dem die Komponenten ausgewählt werden können. Laut dieser Methode sollen nur die Hauptkomponenten ausgewählt werden, die eine Varianz größer als 1 haben. Denn nur diese Komponenten erklären mehr Varianz als eine einzige Variable im Datensatz und führen wirklich zu einer Dimensionsreduktion.

Wie können die Hauptkomponenten interpretiert werden?

Die Hauptkomponenten selbst sind nur sehr schwierig zu interpretieren, da sie als eine Linearkombination der Dimensionen entstehen. Dadurch stellen sie eine gewichtete Mischung mehrer Variablen dar. Jedoch lassen sich in praktischen Anwendungsfällen diese Kombinationen aus Variablen auch konkret interpretieren.

Nehmen wir beispielsweise einen Datensatz mit verschiedenen Informationen zu einzelnen Personen, wie Alter, Gewicht, Größe, Bonität, Einkommen, Ersparnisse und Schulden. In diesem Datensatz könnten sich beispielsweise zwei Hauptkomponenten ausbilden. Die erste Hauptkomponente würde sich vermutlich aus den Dimensionen Bonität, Einkommen, Ersparnisse und Schulden zusammensetzen und hätte für diese Variablen hohe Koeffizienten. Diese Hauptkomponente ließe sich dann beispielsweise als finanzielle Stabilität der Person interpretieren.

Welche Voraussetzungen benötigen wir für die Hauptkomponentanalyse?

Im Vergleich zu ähnlichen statistischen Analysen hat die Principal Component Analysis nur wenige Voraussetzungen, die erfüllt sein müssen, um aussagekräftige Ergebnisse zu liefern. Die grundlegenden Eigenschaften, die der Datensatz aufweisen sollte sind:

• Die Korrelation zwischen den Features sollte linear abbildbar sein.
• Der Datensatz sollte frei von Ausreißern sein, also einzelnen Datenpunkten, die stark von der Masse abweichen.
• Nach Möglichkeit sollten die Variablen stetig sein.
• Das Ergebnis der PCA wird besser, umso größer die Stichprobe ist.

Nicht alle Datensätze können ohne weiteres für eine Principal Component Analysis genutzt werden. Es muss sichergestellt sein, dass die Daten annähernd normalverteilt und intervallskaliert sind, also ein Intervall zwischen zwei numerischen Werten immer den gleichen Abstand hat. Datumsangaben beispielsweise sind intervallskaliert, denn vom 01.01.1980 bis zum 01.01.1981 ist der Zeitabstand genauso groß wie vom 01.01.2020 bis zum 01.01.2021 (Schaltjahre ausgeschlossen). Vor allem die Intervallskalierung muss vom Anwender selbst beurteilt werden und kann nicht durch standardisierte, statistische Tests erfasst werden.

Wie kann man eine Hauptkomponentenanalyse in Python machen?

Es gibt mittlerweile viele Programme mit denen sich Hauptkomponentenanalysen automatisiert berechnen lassen und die Ergebnisse mit verschiedenen Anzahlen von Komponenten verglichen werden kann. In Python funktioniert dies mithilfe des Moduls “Scikit-Learn” dessen Beispiel wir uns hier auch genauer ansehen werden.

In dieser Anwendung wird der sogenannte Iris Dataset genutzt. Es ist ein beliebter Trainingsdatensatz im Bereich des Machine Learnings. Es handelt sich dabei um Daten aus der Biologie, genauer gesagt Informationen von sogenannten Iris Pflanzen. Für jede Blume ist die Länge und Breite des Blüttenblattes und des sogenannten Kelchblattes vorhanden. Die Informationen über die Pflanzen speichern wir in der Variablen X und die Namen der jeweiligen Blume in der Variablen y.

In unserem Fall wollen wir versuchen diese vier Dimensionen auf drei Hauptkomponenten zu reduzieren, um sie in einem dreidimensionalen Diagramm visualisieren zu können. Die tatsächliche Umwandlung der Daten findet in drei Zeilen Code statt. Zuerst müssen wir ein PCA Objekt mit der gewünschten Anzahl der Komponenten aufsetzen. Dieses können wir dann auf unseren Datensatz anpassen und abschließend unsere vierdimensionalen Werte in dreidimensionale Werte umrechnen lassen:

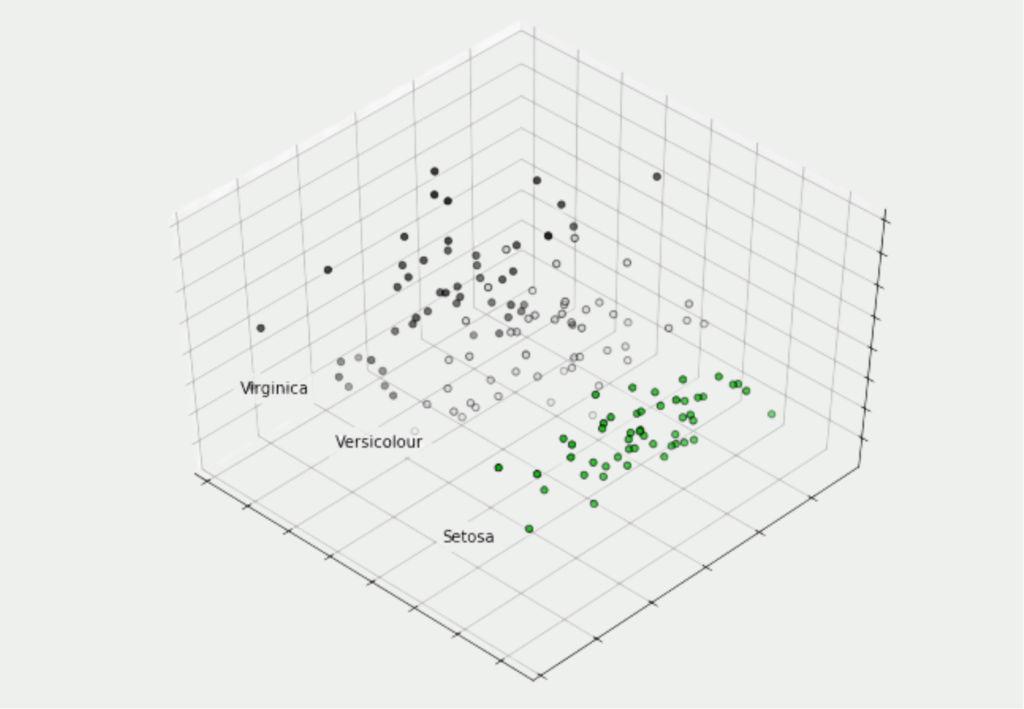
Mithilfe von Matplotlib lassen sich unsere Ergebnisse in einem dreidimensionalen Diagramm veranschaulichen und man sieht, dass auch in drei Dimensionen die Pflanzen derselben Blumenart noch nahe beieinander liegen. Somit ist kein wirklicher Informationsgehalt des Datensatzes verloren gegangen.

tSNE vs. Principal Component Analysis

Obwohl das Ziel von PCA und tSNE erstmal dasselbe ist, nämlich die Dimensionsreduzierung, gibt es einige Unterschiede in den Algorithmen. Zum einen funktioniert tSNE für einen Datensatz sehr gut, kann jedoch nicht auf neue Datenpunkte angewandt werden, da sich dadurch die Abstände zwischen den Datenpunkten verändern und ein neues Ergebnis errechnet werden muss. PCA hingegen erstellt als Ergebnis eine Regel, die auch auf neue Datenpunkte angewandt werden können, die während dem Training noch nicht Teil des Datensatzes waren.

Der t-distributed stochastic neighbor embedding Algorithmus kann auch genutzt werden, wenn die Zusammenhänge zwischen den Datenpunkten nicht-linear sind. Die Principal Component Analysis kann hingegen nur lineare Zusammenhänge erkennen und in die Trennung einbeziehen. Für nicht-lineare Abhängigkeiten kann man auch Neuronale Netzwerke nutzen, deren Aufwand und Training ist jedoch zeitaufwändig. Obwohl tSNE im Vergleich zu PCA auch eine relativ lange Trainingsphase hat, ist sie meist immer noch kürzer als bei Neuronalen Netzwerken und stellt somit einen guten Kompromiss dar.

Ein weiterer wichtiger Unterschied zwischen PCA und tSNE ist der Fokus auf die Datenverteilung. Bei der Principal Component Analysis wird versucht, die globale Anordnung der Datenpunkte auch in weniger Dimensionen beizubehalten. tSNE hingegen fokussiert sich eher auf lokale Abstände und Zusammenhänge, welche auch in niedrigeren Dimensionen beibehalten werden sollen. Deshalb kann es den Anschein machen, dass nach einer Dimensionsreduktion durch tSNE die Daten so aussehen, als seien sie auch schon in Cluster aufgeteilt worden.

Das solltest Du mitnehmen

• Die Principal Component Analysis wird zur Dimensionsreduktion in großen Datensätzen genutzt.
• Sie hilft bei der Vorverarbeitung von Daten für darauf aufbauende Machine Learning Modelle, wie Cluster-Analysen oder Lineare Regressionen.
• Es müssen gewisse Voraussetzungen im Datensatz gegeben sein, damit eine PCA überhaupt möglich ist. Beispielsweise sollte die Korrelation zwischen den Features linear abbildbar sein.

Vielen Dank an Deepnote für das Sponsoring dieses Artikels! Deepnote bietet mir die Möglichkeit, Python-Code einfach und schnell auf dieser Website einzubetten und auch die zugehörigen Notebooks in der Cloud zu hosten.

Andere Beiträge zum Thema Principal Component Analysis

• Eine ausführliche Erklärung zur Hauptkomponentenanalyse inklusive eines anschaulichen Videos, findest Du bei unseren Kollegen von Studyflix.
• Schimmelpfennig, H: Bekannte, aktuelle und neue Anforderungen an Treiberanalysen. In: Keller, B. et al. (Hrsg.): Marktforschung der Zukunft – Mensch oder Maschine?, Wiesbaden, 2016, S. 231-243.
• Kaiser, H. F.: The Application of Electronic Computers to Factor Analysis. In: Educational and Psychological Measurement, Nr. 1/1960, S. 141-151.