Der z-Score, auch Standardwert genannt, ist ein Konzept aus der Statistik, das für die Datenanalyse und Hypothesentests genutzt wird. Er misst, wie viele Standardabweichungen eine einzelne Beobachtung oder ein Datenpunkt vom Mittelwert der Verteilung entfernt ist. Mithilfe des z-Scores können Ausreißer identifiziert werden und außerdem ein Verständnis für die Variabilität der Daten geschaffen werden. Diese Kennzahl wird in verschiedensten Anwendungen eingesetzt, wie beispielsweise in den Bereichen Finanzen, Technik oder Medizin. 

Dieser Beitrag beschäftigt sich mit dem grundlegenden Konzept des z-Scores, der mathematischen Berechnung und den Vor- und Nachteilen der Verwendung. 

Was ist der z-Score?

Der z-Score ist ein statistisches Maß, das auch als Standardwert bezeichnet wird und die Anzahl der Standardabweichungen eines Datenpunkts vom Mittelwert des Datensatzes angibt. Einfach gesprochen misst diese Kennzahl, wie weit ein Datenpunkt vom Mittelwert entfernt ist. Diese Kennzahl wird verwendet, um Daten zu standardisieren und Datensätze untereinander vergleichbar zu machen. Der Datenpunkt selbst ist dafür häufig nicht aussagekräftig genug. 

Das wird an dem folgenden Beispiel aus der Schule besonders deutlich. Zwei Schülerinnen aus verschiedenen Klassen derselben Stufe haben ihre Klausurnote in Mathematik erhalten. Schülern A hat eine 2+ geschrieben, während Schülerin B die Klausur mit der Note 3- zurückerhalten hat. Schülerin A behauptet nun besser in Mathematik zu sein, da eine 2+ eine bessere Note sei als eine 3-. Schülerin B wiederum entgegnet, dass ihre Klausur besonders schwierig gewesen sei und sie deshalb die bessere Mathematikschülerin sei.

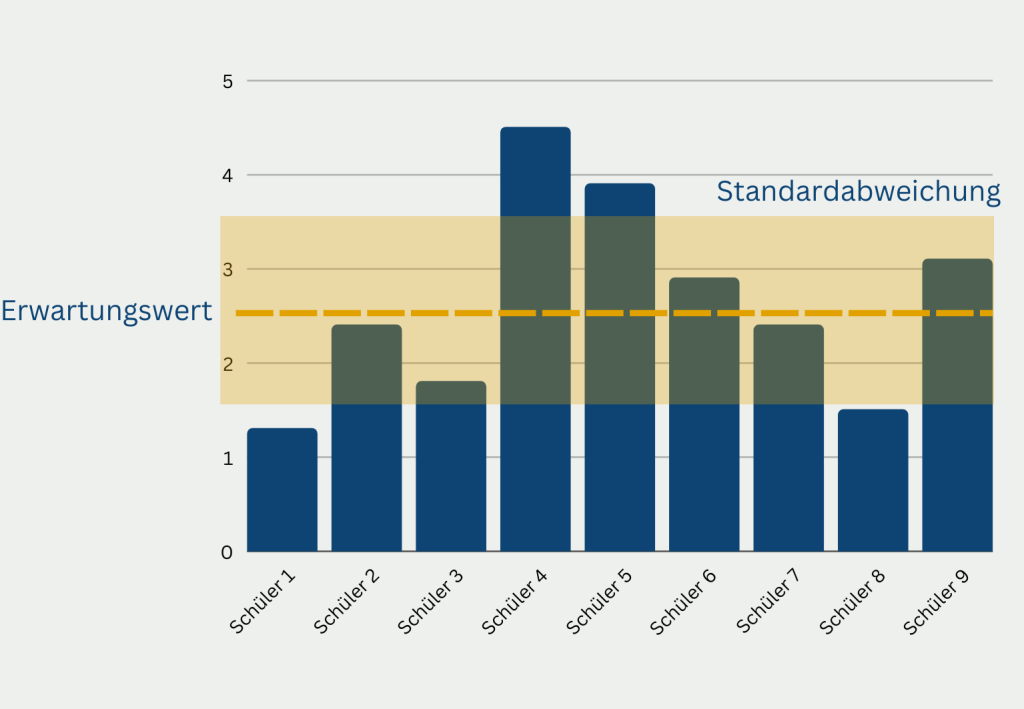
Um diese Behauptung zu stützen, bringt sie an, dass die Klausur in ihrer Klasse eine Durchschnittsnote von 4,0 hatte, während der Durchschnitt in der Klasse von Schülerin A eine 2,0 gewesen sei. Somit habe sie deutlich besser als der Durchschnitt abgeschlossen, im Vergleich zu Schülerin A. Obwohl Schülerin B mit ihrer Aussage im Allgemeinen richtig liegt, muss für einen neutralen Vergleich nicht nur der Durchschnitt der Klasse, sondern auch die Standardabweichung berücksichtigt werden. Dafür kann sie den z-Score nutzen. Wie sich dieser berechnet, wird im nächsten Kapitel genauer erklärt. 

Wie wird der z-Score berechnet?

Die Formel zur Berechnung des z-Scores ist relativ unkompliziert. Als erstes wird die Abweichung des Datenpunktes vom Mittelwert des Datensatzes berechnet. Um diese Differenz noch zu standardisieren und dadurch vergleichbar zu machen, wird sie anschließend durch die Standardabweichung geteilt. Als Formel ergibt sich somit: 

\(\) \[z = \frac{(x – \mu)}{\sigma}\]

Wobei:

• z ist der z-Score
• x ist der Datenpunkt oder -wert
• μ ist der Mittelwert des Datensatzes
• σ ist die Standardabweichung des Datensatzes

Um den z-Score in der Praxis berechnen zu können, müssen die folgenden Schritte ausgeführt werden: 

1. Berechne den Mittelwert (μ) des Datensatzes: Hierfür wird das arithmetische Mittel genutzt. Es werden also alle Datenpunkte addiert und anschließend durch die Gesamtzahl der Datenpunkte geteilt. 
2. Berechne die Standardabweichung (σ) des Datensatzes: Die Standardabweichung misst die durchschnittliche Abweichung eines Datenpunkts vom Mittelwert. Dazu wird für jeden Datenpunkt die Differenz zum Mittelwert errechnet und anschließend quadriert. Diese quadrierten Differenzen werden anschließend zusammenaddiert und durch die Gesamtzahl der Datenpunkte geteilt. Abschließend muss noch die Quadratwurzel dieses Ergebnisses gebildet werden, damit der Wert wieder in derselben Einheit wie der Datensatz ist. 
3. Wähle einen bestimmten Datenpunkt: Der z-Score wird immer für einen bestimmten Datenpunkt und nicht für den kompletten Datensatz berechnet. Für eine Berechnung muss also ein bestimmter Punkt gewählt werden. 
4. Berechne die Differenz zwischen Mittelwert und dem Datenpunkt. 
5. Teile das Ergebnis durch die Standardabweichung (σ).

Ein positiver z-Score bedeutet, dass der gewählte Datenpunkt oberhalb des Mittelwerts liegt und ein negativer Wert, dass er unterhalb des Mittelwerts liegt. Umso größer der absolute Wert ist, umso stärker weicht der Datenpunkt vom Mittelwert ab. Durch diesen Wert kann die relative Position des Datenpunkts in der Verteilung bestimmt werden und es können die Datenpunkte zwischen verschiedenen Datensätzen verglichen werden, auch wenn sich deren absolute Skala in den Daten unterscheidet. 

Wie ist der z-Score an der Standardisierung von Daten beteiligt?

Der z-Score ist ein statistisches Maß, das die Abweichung eines Datenpunktes vom Mittelwert misst, in Abhängigkeit von der Standardabweichung. Es kann für die Standardisierung von Daten genutzt werden, indem der komplette Datensatz von der zugrundeliegenden Skala abstrahiert wird und jeder Datenpunkt noch lediglich durch den dazugehörigen z-Score gemessen wird. Ansonsten können verschiedene Variablen Verzerrungen aufweisen, da sie Skalenunterschiede haben, also in verschiedenen Werten gemessen werden. Ein Datensatz der Haushaltseinkommen in einem Land beispielsweise hat eine absolut höhere Abweichung vom Mittelwert, da diese in Tausend Euro Schritten gemessen wird, als ein Datensatz über die Brotpreise in verschiedenen Städten. 

Durch die Standardisierung mithilfe des z-Scores lassen sich Datensätze besser vergleichen und gegenüberstellen und außerdem können einfacher Muster und Beziehungen in den Daten erkannt werden. Zusätzlich dazu sind die z-Scores nützlich bei der Erkennung von Ausreißern oder anderen ungewöhnlichen Beobachtungen, die sehr weit vom Mittelwert entfernt liegen. 

Welche Anwendungen hat der Score bei Hypothesentests und statistischen Schlussfolgerungen?

Der z-Score spielt eine wichtige Rolle in verschiedenen statistischen Tests. Vor allem in den folgenden Bereichen wird er eingesetzt: 

1. Hypothesentest: Das Ziel eines Hypothesentests ist es zu untersuchen, ob eine Hypothese signifikant von einer Normalverteilung abweicht oder nicht. Mithilfe des z-Scores kann berechnet werden, wie weit der Stichprobenmittelwert vom Mittelwert der Population, also der Normalverteilung abweicht. Dieser Wert kann dann mit einem kritischen Wert der Normalverteilung verglichen werden, um festzustellen, ob sich der Stichprobenwert signifikant vom Populationswert unterscheidet. Wenn dies nicht der Fall ist, wird die Hypothese angenommen. 
2. Konfidenzintervalle: Der z-Score wird außerdem zur Berechnung von Konfidenzintervallen verwendet. Durch diesen Wert eines Stichprobenmittelwerts kann der Wertebereich geschätzt werden, in den der Populationswert mit einer gewissen Wahrscheinlichkeit fällt. 
3. Erkennung von Ausreißern: Durch die Definition eines Schwellenwerts können einfach Ausreißer erkannt werden, indem der z-Score für jeden Datenpunkt berechnet wird. Daten, deren Werte außerhalb eines definierten Bereichs liegen können als Ausreißer klassifiziert werden. 
4. Normalitätstests: Der z-Score ermöglicht außerdem, dass geprüft werden kann, ob Daten einer Normalverteilung folgen. Mithilfe dieser Berechnung und der Veranschaulichung der Verteilung in einem Normalwahrscheinlichkeitsdiagramm kann beurteilt werden, ob eine Normalverteilung vorliegt. 

Der z-Score bildet die Basis für viele statistische Anwendungen. Vor allem bei Hypothesentests und bei der Prüfung der Normalverteilung wird er eingesetzt. 

Wie ist der z-Score zu interpretieren?

Der z-Score lässt sich relativ einfach interpretieren. Dazu werden zwei Größen betrachtet, zum einen das Vorzeichen und zum anderen der tatsächliche Wert. Ein positiver Wert bedeutet, dass der Datenpunkt oberhalb des Mittelwerts liegt, während ein negativer Wert aussagt, dass der Datenpunkt unterhalb des Mittelwerts liegt. Die Größe des z-Scores wiederum misst, wie weit der Datenpunkt vom Mittelwert entfernt liegt. Für eine bessere Vergleichbarkeit wird dies in Standardabweichungen und nicht in absoluten Zahlen gemessen. 

Ein z-Score von 1 bedeutet somit, dass der Punkt oberhalb des Mittelwerts für den Datensatz liegt und außerdem eine Standardabweichung entfernt ist. Ein Wert von 2 kann genauso interpretiert werden. Dieser Datenpunkt ist also zwei Standardabweichungen oberhalb des Mittelwerts gelegen. Schließlich liegt ein Datenpunkt mit dem z-Score -1 unterhalb des Mittelwerts und zwar eine Standardabweichung entfernt. 

Was sind die Vor- und Nachteile des Scores?

Der z-Score ist ein beliebtes Tool im Bereich der Statistik, das dazu genutzt wird, Daten aus verschiedenen Quellen zu standardisieren und damit Datensätze vergleichbar zu machen. Jedoch hat diese Kennzahl nicht nur Vorteile, sondern weist auch einige Grenzen. Deshalb befassen wir uns in diesem Abschnitt mit den Vor- und Nachteilen des z-Scores, sodass er je nach Anwendung effektiv eingesetzt werden kann. 

Vorteile:

• Der z-Score bietet ein einfaches und standardisiertes Maß, um beurteilen zu können, wie weit ein Datenpunkt vom Durchschnitt des Datensatzes entfernt liegt. 
• Dadurch ist sichergestellt, dass sich verschiedene Datensätze unabhängig und auf einer einheitlichen Skala vergleichen lassen. 
• Außerdem ist der z-Score eine sinnvolle Möglichkeit, um Ausreißer oder Extremwerte in einem Datensatz zu erkennen. 
• Diese Kennzahl kann in zahlreichen Anwendungen, wie beispielsweise bei Hypothesentests, verwendet werden, um statistische Schlussfolgerungen zu ziehen und zu entscheiden, ob eine Hypothese abgelehnt werden sollte. 

Nachteile:

• Der z-Score basiert auf einer Normalverteilung und setzt voraus, dass der Datensatz einer Normalverteilung folgt. In manchen Fällen kann diese Annahme nicht zutreffen. 
• Die Kennzahl basiert auf dem Durchschnitt, der durch Ausreißer beeinflusst werden kann. Dadurch wird auch der z-Score selbst indirekt von Ausreißern beeinflusst. 
• Bei kleinen Datensätzen muss man mit der Verwendung dieser Kennzahl vorsichtig sein, da möglicherweise die Verteilung nicht ausreichend etabliert ist und deshalb keine aussagekräftigen Werte zustande kommen. 

Welche alternativen statistischen Maße können stattdessen verwendet oder kombiniert werden?

Je nach Anwendung kann der z-Score nicht das optimale Maß sein oder sollte für eine ausgewogene Analyse durch andere Kennzahlen ergänzt werden. Die beliebtesten Kennzahlen dafür sind: 

• T-Score: Dieser ist ein ähnliches Maß wie der z-Score, das genauso die Anzahl der Standardabweichungen zum Mittelwert misst. Er wird in der Regel für kleinere Stichproben genutzt, in denen der z-Score möglicherweise keine guten Ergebnisse liefert. 
• Perzentile: Die Perzentile sind eine Möglichkeit, Datenpunkte anhand ihrer relativen Position innerhalb der Verteilung einzustufen. Das 75. Perzentil beispielsweise umfasst alle Datenpunkte, die unter 75 % der Daten fallen. 
• Effektgrößen: Die Effektgrößen quantifizieren das Ausmaß, welches der Unterschied zwischen zwei Variablen angenommen hat. Diese finden Anwendung, um Ergebnisse zwischen Datensätzen mit unterschiedlichen Messgrößen oder Skalen zu vergleichen. 
• Konfidenzintervalle: Die Konfidenzintervalle geben einen Bereich an, in den der wahre Parameter der Population voraussichtlich fällt. Diese können verwendet werden, um Schätzungen zu bewerten und Ergebnisse von Studien zu vergleichen. 

Der z-Score ist vor allem bei Hypothesentests ein weit verbreitetes Instrument. Er kann jedoch auch durch andere Kennzahlen ersetzt werden, um Datensätze zu vergleichen. 

Das solltest Du mitnehmen

• Der z-Score ist eine Kennzahl in der Statistik mit der bestimmt wird, wie weit ein Datenpunkt vom Mittelwert eines Datensatzes enfernt liegt. Diese Entfernung wird in Standardabweichungen gemessen. 
• Diese Kennzahl wird zur Standardisierung von Daten eingesetzt und außerdem können damit Datensätze in unterschiedlichen Skalen verglichen werden. 
• Zur Anwendung kommt dieses Maß häufig in Hypothesentests und bei statistischen Schlussfolgerungen. Vor allem dann, wenn der Populationswert und die Standardabweichung kann ist.
• Der z-Score ist eine besonders einfache Kennzahl in der Berechnung und Interpretation. Jedoch hat er auch seine Nachteile, da er zum Beispiel sehr abhängig vom Populationsparameter ist und außerdem empfindlich gegenüber Ausßreißern. 
• Es können auch andere statistische Maße zum Einsatz kommen, wie beispielsweise der t-Score oder Konfidenzintervalle. Diese können entweder als Alternative oder in Verbindung mit dem z-Score genutzt werden. 

Andere Beiträge zum Thema z-Score

Das Maß kann auch in Python mit einer Bibliothek wie SciPy berechnet werden. Die Dokumentation dazu findest Du hier.