Im Bereich der Datenanalyse ist das Verständnis der Beziehungen zwischen den Variablen oft der Schlüssel zur Entschlüsselung wertvoller Erkenntnisse. Willkommen in der Welt der bivariaten Analyse, bei der sich der Schwerpunkt von einzelnen Variablen auf das dynamische Zusammenspiel zwischen Paaren von Variablen verlagert. Diese Analysetechnik ist ein Eckpfeiler der statistischen Untersuchung, der es uns ermöglicht, tiefer in die Daten einzudringen, Verbindungen herzustellen und fundierte Entscheidungen zu treffen.

Stelle Dir vor, Du untersuchst die Auswirkungen von Werbeausgaben auf Produktverkäufe oder erforschst, wie die Leistung von Studenten mit den Studienzeiten zusammenhängt. Die bivariate Analyse ist Dein zuverlässiger Kompass, der Dich durch das verschlungene Terrain der Assoziationen, Abhängigkeiten und Korrelationen führt.

In diesem Artikel begeben wir uns auf eine Reise in das Herz der bivariaten Analyse. Wir befassen uns mit den grundlegenden Konzepten, praktischen Methoden und realen Anwendungen. Ganz gleich, ob Du ein Datenenthusiast, ein Forscher oder ein Geschäftsmann bist, der die Geheimnisse Deiner Datensätze lüften möchte: Begleite uns durch die Welt der bivariaten Analyse und mache Dir die Macht zweier Variablen zunutze, die zusammenarbeiten.

Was ist eine bivariate Analyse?

Die bivariate Analyse ist eine statistische Methode, die in der Datenanalyse und Forschung eingesetzt wird, um die Beziehung zwischen zwei Variablen zu untersuchen. Im Gegensatz zur univariaten Analyse, die sich jeweils auf eine einzige Variable konzentriert, wird bei der bivariaten Analyse untersucht, wie zwei verschiedene Variablen zusammenwirken oder sich gegenseitig beeinflussen.

Im Kern geht es bei der bivariaten Analyse um die Beantwortung von Fragen wie:

• Entspricht die Veränderung einer Variablen der Veränderung einer anderen Variablen?
• Sind die beiden Variablen in irgendeiner Weise miteinander verbunden?
• Kann eine Variable auf der Grundlage der Werte der anderen Variable vorhergesagt oder erklärt werden?

Dieser analytische Ansatz ist in verschiedenen Bereichen besonders wertvoll, z. B. in den Wirtschafts- und Sozialwissenschaften, im Gesundheitswesen und im Marketing, wo das Verständnis der Zusammenhänge zwischen den Variablen für fundierte Entscheidungen von entscheidender Bedeutung ist.

Die bivariate Analyse kann viele Formen annehmen, je nach Art der untersuchten Variablen. Einige gängige Szenarien sind:

• Kontinuierlich vs. Kontinuierlich: Wenn beide untersuchten Variablen kontinuierlich (numerisch) sind, verwenden Forscher häufig Techniken wie Korrelationsanalysen oder Streudiagramme, um die Stärke und Richtung der Beziehung zu visualisieren und zu messen.
• Kategorisch vs. kategorisch: In Fällen, in denen beide Variablen kategorisch (nicht numerisch) sind, helfen Methoden wie Chi-Quadrat-Unabhängigkeitstests dabei festzustellen, ob ein signifikanter Zusammenhang zwischen den beiden Variablen besteht.
• Kontinuierlich vs. kategorial: Wenn eine Variable kontinuierlich und die andere kategorial ist, werden Verfahren wie t-Tests oder Varianzanalysen (ANOVA) eingesetzt, um Mittelwerte zwischen verschiedenen Kategorien oder Gruppen zu vergleichen.
• Bivariate Zeitreihenanalyse: Bei Zeitreihendaten können Forscher untersuchen, wie sich Veränderungen einer Variablen im Laufe der Zeit auf eine andere Variable auswirken. Dies kann Techniken wie Kreuzkorrelation oder Granger-Kausalitätstests beinhalten.

Die bivariate Analyse dient als grundlegender Baustein für komplexere multivariate Analysen und Modellierungen. Sie ermöglicht es Forschern und Analysten, wertvolle Einblicke in die Abhängigkeiten und Wechselwirkungen zwischen Variablen zu gewinnen und ebnet so den Weg für eine fundiertere Entscheidungsfindung und ein tieferes Verständnis der zugrunde liegenden Muster in den Daten.

Was sind die verschiedenen Arten der bivariaten Analyse?

Die bivariate Analyse umfasst eine Vielzahl von Techniken, die jeweils dazu dienen, die Beziehung zwischen zwei verschiedenen Variablen zu untersuchen. Die Wahl der zu verwendenden Methode hängt von der Art der Variablen, mit denen Du arbeitetst, und von den Forschungsfragen ab, die Du beantworten willst. Hier sind einige gängige Arten der bivariaten Analyse:

• Korrelationsanalyse: Dies ist eine der am häufigsten verwendeten Techniken zur Untersuchung der Beziehung zwischen zwei kontinuierlichen Variablen. Der Pearson-Korrelationskoeffizient misst die Stärke und Richtung einer linearen Beziehung. Ein Wert nahe 1 weist auf eine starke positive Korrelation hin, ein Wert nahe -1 auf eine starke negative Korrelation und ein Wert nahe 0 auf eine geringe bis keine Korrelation.
• Streudiagramme: Streudiagramme sind grafische Darstellungen von Datenpunkten in einem zweidimensionalen Raum. Sie sind besonders nützlich für die Visualisierung der Beziehung zwischen zwei kontinuierlichen Variablen. Das Muster der Punkte auf dem Streudiagramm kann Aufschluss über die Art der Beziehung geben.
• Kovarianz: Die Kovarianz ist ein statistisches Maß, mit dem beurteilt wird, wie sich zwei kontinuierliche Variablen gemeinsam verändern. Sie gibt die Richtung der linearen Beziehung an (positiv oder negativ), bietet jedoch kein standardisiertes Maß wie Korrelationskoeffizienten.
• Chi-Quadrat-Test: Bei zwei kategorialen Variablen ist der Chi-Quadrat-Test auf Unabhängigkeit eine gängige Wahl. Mit ihm lässt sich feststellen, ob ein signifikanter Zusammenhang zwischen den beiden Variablen besteht. Er kann zum Beispiel verwendet werden, um zu analysieren, ob ein Zusammenhang zwischen dem Geschlecht und den Wahlpräferenzen besteht.
• T-Test: Der t-Test wird verwendet, wenn Du die Mittelwerte von zwei Gruppen für eine kontinuierliche Variable vergleichen möchtest. Du kannst zum Beispiel einen t-Test verwenden, um festzustellen, ob ein signifikanter Unterschied in den Testergebnissen von zwei verschiedenen Lehrmethoden besteht.
• Varianzanalyse (ANOVA): Die ANOVA ist eine Erweiterung des t-Tests und wird verwendet, wenn mehr als zwei Gruppen zu vergleichen sind. Sie prüft, ob es statistisch signifikante Unterschiede zwischen den Mittelwerten von drei oder mehr Gruppen gibt.
• Regressionsanalyse: Die bivariate Regressionsanalyse wird zur Modellierung und Vorhersage der Beziehung zwischen einer abhängigen und einer unabhängigen Variable verwendet. Sie könnten zum Beispiel eine einfache lineare Regression verwenden, um vorherzusagen, wie sich Temperaturänderungen (unabhängige Variable) auf den Eisverkauf (abhängige Variable) auswirken.
• Logistische Regression: Diese Technik ist geeignet, wenn die Ergebnisvariable binär ist (z. B. ja/nein, Erfolg/Misserfolg). Die logistische Regression hilft, die Beziehung zwischen einer oder mehreren Prädiktorvariablen und der Wahrscheinlichkeit des binären Ergebnisses zu verstehen.
• Spearman’s Rangordnungs-Korrelation: Bei ordinalen oder nicht-normalverteilten kontinuierlichen Variablen bietet die Spearman-Korrelation ein nicht-parametrisches Maß für die Assoziation. Sie basiert auf der Rangfolge der Datenpunkte und nicht auf deren tatsächlichen Werten.

Dies sind nur einige Beispiele für die vielen verfügbaren bivariaten Analyseverfahren. Die Wahl der Methode hängt von den Datentypen, den Forschungszielen und den Annahmen ab, die Du über Deine Daten machen willst. Eine ordnungsgemäß durchgeführte bivariate Analyse kann wertvolle Einblicke in die Beziehungen zwischen den Variablen liefern, die als Grundlage für die Entscheidungsfindung und für die weitere Forschung dienen.

Was sind Streudiagramme und Streuungsdiagramme?

Im Bereich der bivariaten Analyse sind Punktdiagramme und Streudiagramme unverzichtbare Hilfsmittel für die visuelle Untersuchung und das Verständnis der Beziehung zwischen zwei kontinuierlichen Variablen. Diese grafischen Darstellungen bieten wertvolle Einblicke in Muster, Trends und potenzielle Zusammenhänge in Ihren Daten.

Was ist ein Scatterplot?

Ein Scatterplot, auch als Streudiagramm oder Streudiagramm bekannt, ist eine zweidimensionale grafische Darstellung von Datenpunkten. Bei der bivariaten Analyse wird jeder Datenpunkt als Punkt auf einer kartesischen Ebene dargestellt, wobei eine Variable auf der x-Achse (horizontal) und die andere auf der y-Achse (vertikal) aufgetragen wird.

Wie man ein Streudiagramm erstellt:

Die Erstellung eines Streudiagramms ist ganz einfach:

• Datenvorbereitung: Stelle sicher, dass Du einen Datensatz mit zwei kontinuierlichen Variablen hast, die Du zusammen analysieren möchtest.
• Achsen auswählen: Wähle aus, welche Variable auf der x-Achse und welche auf der y-Achse erscheinen soll, je nach Deiner Forschungsfrage und der Rolle der Variablen.
• Datenpunkte aufzeichnen: Suche für jeden Datenpunkt die entsprechenden Werte der beiden Variablen und setze einen Punkt an den Schnittpunkt der entsprechenden x- und y-Werte.
• Achsen beschriften: Beschrifte die x-Achse und die y-Achse, um die dargestellten Variablen zu kennzeichnen.

Interpretieren eines Streudiagramms:

Zur Interpretation eines Streudiagramms gehört es, das Muster der Punkte zu untersuchen und Trends zu erkennen:

• Richtung: Achte auf die allgemeine Richtung der Punkte. Neigen sie sich von links nach rechts nach oben, was auf eine positive Korrelation hinweist? Oder sind sie abwärts geneigt, was auf eine negative Korrelation hindeutet?
• Stärke: Beurteile den Grad der Streuung oder Häufung der Punkte. Eine enge Anhäufung deutet auf eine starke Korrelation hin, während ein verstreutes Muster auf eine schwache Korrelation hindeutet.
• Ausreißer: Identifiziere alle Datenpunkte, die weit von der Hauptgruppe der Punkte entfernt liegen. Ausreißer können einen Einfluss auf die Analyse haben und erfordern möglicherweise weitere Untersuchungen.
• Linearität: Prüfe, ob die Datenpunkte ein lineares Muster bilden. Ist dies der Fall, besteht möglicherweise eine lineare Beziehung zwischen den beiden Variablen. Wenn nicht, ist die Beziehung möglicherweise nichtlinear.

Anwendungsfälle von Streudiagrammen in der bivariaten Analyse:

• Bewertung der Korrelation: Streudiagramme werden häufig verwendet, um die Stärke und Richtung der Beziehung zwischen zwei kontinuierlichen Variablen zu bewerten. Eine starke positive Korrelation erscheint als eine dichte Ansammlung von Punkten, die nach oben geneigt sind, während eine starke negative Korrelation als eine dichte Ansammlung von Punkten erscheint, die nach unten geneigt sind.
• Ausreißer-Erkennung: Ausreißer, d. h. Datenpunkte, die sich deutlich von den anderen unterscheiden, lassen sich auf einem Streudiagramm leicht erkennen. Ihr Vorhandensein kann auf Probleme mit der Datenqualität oder auf einzigartige Beobachtungen hinweisen, die besondere Aufmerksamkeit erfordern.
• Erkennung von Mustern: Streudiagramme helfen bei der Erkennung von Mustern, wie z. B. Saisonalität in Zeitreihendaten, zyklisches Verhalten oder lineare Trends. Diese Muster können bei der Entscheidungsfindung helfen und die weitere Analyse leiten.
• Erkennung von Heteroskedastizität: Bei der Regressionsanalyse können Streudiagramme Heteroskedastizität aufzeigen, d. h. eine Situation, in der die Streuung der Datenpunkte systematisch mit der unabhängigen Variable variiert. Diese Information ist für die Modellauswahl und -interpretation von entscheidender Bedeutung.

Zusammenfassend lässt sich sagen, dass Streudiagramme und Streuungsdiagramme eine zentrale Rolle bei der bivariaten Analyse spielen, da sie ein visuelles Mittel zur Untersuchung und Interpretation der Beziehung zwischen zwei kontinuierlichen Variablen bieten. Diese Visualisierungen dienen als Grundlage für fortgeschrittenere statistische Analysen und unterstützen Entscheidungsprozesse in verschiedenen Bereichen, von Wirtschaft und Finanzen bis hin zu Gesundheitswesen und Umweltwissenschaften.

Was ist die Korrelationsanalyse?

Die Korrelationsanalyse ist eine grundlegende Komponente der bivariaten Analyse, die darauf abzielt, die Stärke und Richtung der Beziehung zwischen zwei kontinuierlichen Variablen zu quantifizieren und zu verstehen. Sie bietet wertvolle Einblicke in die Art und Weise, wie Veränderungen in einer Variablen mit Veränderungen in einer anderen verbunden sein können.

Bei der Korrelationsanalyse wird ein Korrelationskoeffizient berechnet, in der Regel der Pearsonsche Korrelationskoeffizient (oft als “r” bezeichnet), um die lineare Beziehung zwischen zwei Variablen zu quantifizieren. Dieser Koeffizient gibt Aufschluss über die folgenden Aspekte der Beziehung:

1. Stärke: Die Größe des Korrelationskoeffizienten gibt an, wie stark die Beziehung ist. Ein Koeffizient nahe bei 1 bedeutet eine starke positive Korrelation, während ein Koeffizient nahe bei -1 eine starke negative Korrelation anzeigt. Ein Koeffizient nahe 0 deutet auf eine schwache oder keine lineare Korrelation hin.
2. Richtung: Das Vorzeichen des Korrelationskoeffizienten (+ oder -) gibt die Richtung der Beziehung an. Ein positiver Koeffizient deutet auf eine positive Korrelation hin, d. h., wenn eine Variable zunimmt, nimmt auch die andere tendenziell zu. Umgekehrt bedeutet ein negativer Koeffizient eine negative Korrelation, bei der eine Variable tendenziell abnimmt, wenn die andere zunimmt.

Interpretation von Korrelationskoeffizienten:

Der Korrelationskoeffizient reicht von -1 bis 1:

• Positive Korrelation (r > 0): Wenn “r” größer als 0 ist, deutet dies darauf hin, dass bei einem Anstieg der einen Variablen die andere tendenziell ebenfalls ansteigt. Je näher “r” bei 1 liegt, desto stärker ist die positive Korrelation.
• Negative Korrelation (r < 0): Ein Korrelationskoeffizient, der kleiner als 0 ist, bedeutet, dass die eine Variable zunimmt, während die andere abnimmt. Je näher “r” bei -1 liegt, desto stärker ist die negative Korrelation.
• Keine Korrelation (r = 0): Wenn der Korrelationskoeffizient nahe bei 0 liegt, deutet dies auf eine geringe oder gar keine lineare Beziehung zwischen den Variablen hin.

Erstellen eines Streudiagramms zur Korrelationsvisualisierung:

Vor der Berechnung des Korrelationskoeffizienten ist es üblich, ein Streudiagramm zu erstellen, um die Beziehung zwischen den beiden Variablen zu visualisieren. Streudiagramme helfen Dir, die Linearität der Beziehung zu beurteilen, Ausreißer zu erkennen und Muster zu identifizieren.

Anwendungsfälle der Korrelationsanalyse in der bivariaten Analyse:

• Stärke der Assoziation: Die Korrelationsanalyse wird verwendet, um die Stärke der Beziehung zwischen Variablen zu bestimmen. Im Finanzwesen kann sie beispielsweise die Beziehung zwischen Zinssätzen und Aktienmarktrenditen quantifizieren.
• Modellbildung: Bei der prädiktiven Modellierung hilft das Verständnis der Korrelationen zwischen Variablen bei der Auswahl relevanter Prädiktoren für ein Modell. Stark korrelierte Variablen können redundant sein.
• Qualitätskontrolle: In der Fertigung kann die Korrelationsanalyse Variablen identifizieren, die stark miteinander verbunden sind, was auf ein Qualitätskontrollproblem hinweisen kann, das Aufmerksamkeit erfordert.
• Gesundheitswesen: In der medizinischen Forschung kann die Korrelationsanalyse verwendet werden, um die Beziehung zwischen Faktoren wie der Ernährung und den gesundheitlichen Ergebnissen zu bewerten.
• Sozialwissenschaften: In der Soziologie oder Psychologie kann die Korrelationsanalyse Zusammenhänge zwischen Variablen wie Einkommen und Zufriedenheit untersuchen.
• Umweltstudien: Die Korrelationsanalyse kann Zusammenhänge zwischen Umweltfaktoren wie dem Verschmutzungsgrad und der öffentlichen Gesundheit aufzeigen.

Es ist wichtig zu beachten, dass Korrelation nicht gleichbedeutend mit Kausalität ist. Eine Korrelation deutet zwar auf einen Zusammenhang zwischen zwei Variablen hin, beweist aber nicht, dass Veränderungen bei einer Variablen Veränderungen bei der anderen verursachen. Der Nachweis der Kausalität erfordert oft zusätzliche Forschung und Experimente.

Zusammenfassend lässt sich sagen, dass die Korrelationsanalyse ein leistungsfähiges Instrument der bivariaten Analyse zur Quantifizierung und Interpretation der Beziehung zwischen zwei kontinuierlichen Variablen ist. Sie liefert wertvolle Erkenntnisse darüber, wie die Variablen zusammenhängen, was für fundierte Entscheidungen in verschiedenen Studienbereichen und Industriezweigen unerlässlich ist.

Was ist eine Regressionsanalyse?

Die Regressionsanalyse ist ein statistisches Verfahren, das bei der bivariaten Analyse eingesetzt wird, um die Beziehung zwischen zwei kontinuierlichen Variablen zu untersuchen. Im Gegensatz zur Korrelationsanalyse, die die Stärke und Richtung einer Beziehung quantifiziert, geht die Regressionsanalyse einen Schritt weiter, indem sie die Beziehung modelliert und auf der Grundlage dieses Modells Vorhersagen macht.

Bei der Regressionsanalyse wird ein mathematisches Modell an die Daten angepasst, um zu beschreiben, wie sich eine Variable (die abhängige oder Reaktionsvariable) im Verhältnis zu einer anderen Variablen (der unabhängigen oder Prädiktorvariable) verändert. Ziel ist es, das am besten passende Modell zu finden, das die Beziehung zwischen den beiden Variablen erklärt.

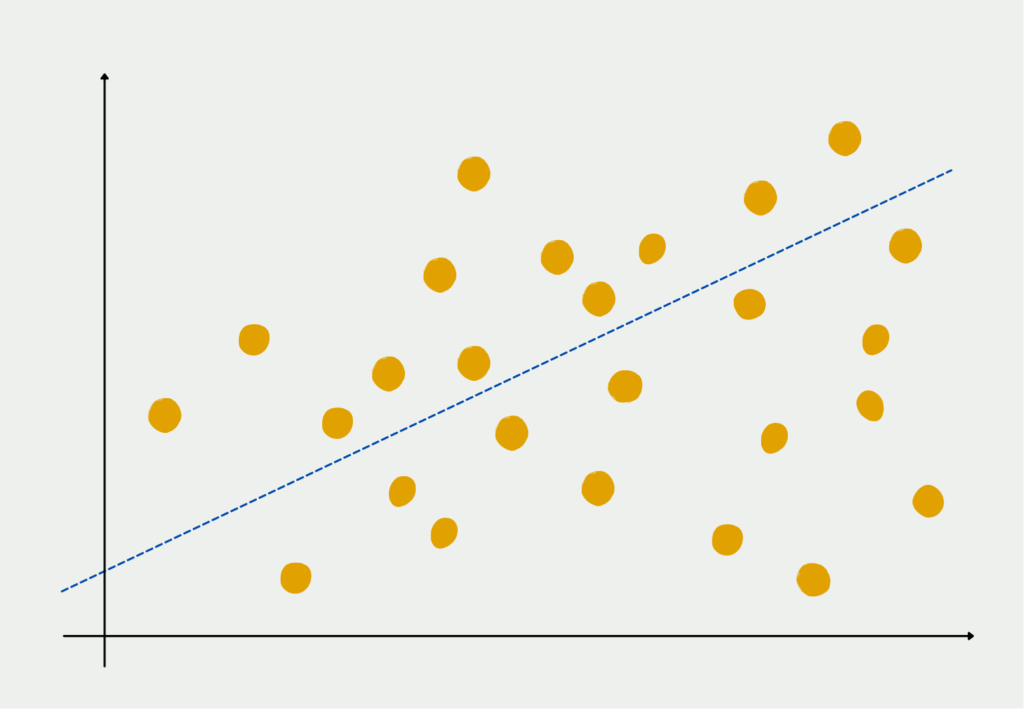
Schlüsselelemente der Regressionsanalyse:

1. Abhängige Variable: Die Variable, die Du vorhersagen oder erklären willst, wird als abhängige Variable (Y) bezeichnet. Sie ist die Ergebnisvariable oder das, was Du zu verstehen versuchst.
2. Unabhängige Variable: Die Variable, von der Du glaubst, dass sie Veränderungen in der abhängigen Variable beeinflusst oder erklärt, ist die unabhängige Variable (X). Sie ist die Vorhersagevariable.
3. Regressionsmodell: Das Regressionsmodell ist eine mathematische Gleichung, die die Beziehung zwischen der abhängigen und der unabhängigen Variable darstellt. Die einfachste Form ist das lineare Regressionsmodell, bei dem eine lineare Beziehung zwischen den Variablen angenommen wird:

\(\) \[ y = \beta_{0} + \beta_{1} \cdot X + \epsilon \]

• Y ist die abhängige Variable.
• X ist die unabhängige Variable.
• β₀ ist der Achsenabschnitt (der Wert von Y, wenn X gleich 0 ist).
• β₁ ist die Steigung (wie stark sich Y bei einer Änderung von X um eine Einheit ändert).
• ε ist der Fehlerterm (unerklärte Variabilität).

β₀ und β₁ sind die Parameter des Regressionsmodells. Sie werden anhand der Daten geschätzt, um die beste Anpassungslinie zu finden, die die Summe der quadrierten Fehler (die Unterschiede zwischen den beobachteten und den vorhergesagten Werten) minimiert.

Interpretation der Regressionsanalyse:

Die Regressionsanalyse bietet Einblicke in die folgenden Aspekte der Beziehung zwischen Variablen:

• Stärke und Signifikanz: Der Koeffizient β₁ gibt die Stärke und Richtung der Beziehung an. Ein positives β₁ deutet darauf hin, dass mit einem Anstieg von X auch Y tendenziell zunimmt, während ein negatives β₁ das Gegenteil bedeutet. Die Größe von β₁ spiegelt den Grad der Auswirkung wider.
• Vorhersage: Mit der Regressionsanalyse kannst Du den Wert der abhängigen Variable für einen bestimmten Wert der unabhängigen Variable vorhersagen. Diese Vorhersagefähigkeit ist in verschiedenen Bereichen wertvoll, z. B. im Finanzwesen (Vorhersage von Aktienkursen), in der Wirtschaft (Vorhersage von Inflationsraten) und im Gesundheitswesen (Vorhersage von Patientenergebnissen).

Anwendungsfälle der Regressionsanalyse in der bivariaten Analyse:

• Wirtschaft: Vorhersage der Beziehung zwischen Faktoren wie Einkommen und Ausgaben oder Beschäftigungsquoten und Wirtschaftswachstum.
• Gesundheitswesen: Modellierung der Auswirkungen von Variablen wie Ernährung und Bewegung auf gesundheitliche Ergebnisse wie Gewichtsverlust oder Blutdruck.
• Marketing: Analyse des Einflusses von Werbeausgaben auf den Produktabsatz.
• Umweltwissenschaft: Verständnis der Beziehung zwischen Verschmutzungsgrad und Artenvielfalt.
• Ingenieurwesen: Vorhersage der Beziehung zwischen Variablen wie Temperatur und Materialfestigkeit.

Es ist wichtig, die Regressionsanalyse mit Vorsicht durchzuführen und mögliche Einschränkungen zu berücksichtigen. Korrelation bedeutet nicht gleich Kausalität, und Regressionsergebnisse sollten nicht ohne weitere Beweise als kausale Beziehungen interpretiert werden. Außerdem sollten die Annahmen des Regressionsmodells, wie Linearität und Homoskedastizität, geprüft werden.

Zusammenfassend lässt sich sagen, dass die Regressionsanalyse ein leistungsstarkes Instrument der bivariaten Analyse ist, das über die Korrelation hinausgeht, indem es die Beziehung zwischen zwei kontinuierlichen Variablen modelliert und vorhersagt. Sie wird in vielen Bereichen eingesetzt, um Daten zu verstehen, zu erklären und Vorhersagen zu treffen.

Das solltest Du mitnehmen

• Die bivariate Analyse ist eine grundlegende statistische Technik, die Beziehungen und Assoziationen zwischen zwei Variablen aufdeckt.
• Durch die Korrelationsanalyse können wir die Stärke und Richtung der Beziehungen quantifizieren. Eine positive, negative oder gar keine Korrelation liefert wertvolle Erkenntnisse.
• Streudiagramme sind ein leistungsstarkes Instrument zur Visualisierung bivariater Daten. Sie ermöglichen es uns, Muster und Trends zu erkennen, indem wir Datenpunkte in ein Diagramm einzeichnen.
• Die Regressionsanalyse hebt die bivariate Analyse auf die nächste Stufe, indem sie die Beziehung modelliert und Vorhersagen macht. Sie ist eine vielseitige Technik, die in verschiedenen Bereichen eingesetzt wird.
• Die bivariate Analyse wird unter anderem in den Bereichen Wirtschaft, Gesundheitswesen, Marketing, Umweltwissenschaften und Technik eingesetzt.
• Die bivariate Analyse ist zwar wertvoll, aber sie impliziert keine Kausalität. Es ist wichtig, die Ergebnisse mit Vorsicht zu interpretieren und die zugrunde liegenden Annahmen zu berücksichtigen.
• Die bivariate Analyse unterstützt die datengestützte Entscheidungsfindung, indem sie Einblicke in die Beziehung zwischen zwei Variablen gewährt, was für das Verständnis komplexer Systeme und für fundierte Entscheidungen unerlässlich ist.
• Die bivariate Analyse dient als Grundlage für die fortgeschrittene multivariate Analyse, bei der die Beziehungen zwischen mehreren Variablen untersucht werden.

Andere Beiträge zum Thema Bivariate Analyse

Die University of West Georgia hat einen interessanten Artikel zum Thema bivariate Analyse verfasst, den Du hier finden kannst.