In der Welt der Datenanalyse ist die univariate Analyse der erste Schritt, das Fundament und die Kunst des Verstehens von Daten, eine Variable nach der anderen. Diese grundlegende Technik enthüllt die Geschichten, die in einzelnen Datenpunkten verborgen sind, bevor wir uns mit komplexen multivariaten Beziehungen befassen.

In diesem Artikel werden wir die Kernkonzepte der univariaten Analyse erkunden, von den Datentypen bis zu Visualisierungstechniken und statistischen Maßen. Du wirst erfahren, wie man Rohdaten in sinnvolle Erkenntnisse verwandelt, um wertvolle Fähigkeiten für verschiedene Bereiche zu erlangen, von Finanzen bis zur Gesundheitsversorgung und darüber hinaus.

Was ist die univariate Analyse?

Die univariate Analyse ist eine grundlegende Technik in der Datenanalyse, die sich darauf konzentriert, die Merkmale einer einzelnen Variable isoliert zu untersuchen und zusammenzufassen. Dabei geht es darum, ein einzelnes Datenattribut oder eine Variable zu betrachten, ohne die Beziehungen oder Korrelationen zu anderen Variablen zu berücksichtigen. Das Hauptziel der univariaten Analyse besteht darin, Einblicke in die Verteilung, Muster und Eigenschaften einzelner Variablen in einem Datensatz zu gewinnen.

Zu den wichtigsten Komponenten der univariaten Analyse gehören:

• Datenexploration: Dieser Schritt beinhaltet das Verständnis der Art der Variable, ihres Datentyps (z. B. numerisch oder kategorisch) und des Wertebereichs, den sie annehmen kann. Bei numerischen Variablen werden Maße wie Mittelwert, Median, Varianz und Verteilungsform untersucht. Bei kategorischen Variablen wird die Häufigkeit jeder Kategorie betrachtet.
• Datenvisualisierung: Visuelle Darstellungen wie Histogramme, Balkendiagramme, Boxplots und Tortendiagramme werden verwendet, um die Verteilung und die Merkmale der Variable zu veranschaulichen. Diese Visualisierungen helfen Analysten dabei, Muster, Ausreißer und Trends in den Daten zu identifizieren.
• Zusammenfassende Statistiken: Die univariate Analyse berechnet zusammenfassende Statistiken, die eine prägnante Beschreibung der zentralen Tendenz (z. B. Mittelwert) und der Streuung (z. B. Standardabweichung) der Variable liefern. Diese Statistiken bieten einen Einblick in das Verhalten der Variable.
• Datentransformation: In einigen Fällen können Datenverarbeitungstechniken wie Skalierung, Normalisierung oder Logarithmus-Transformation angewendet werden, um die Variable für die Analyse oder Modellierung besser geeignet zu machen.
• Hypothesentests: Die univariate Analyse kann Hypothesentests umfassen, um festzustellen, ob die Verteilung oder die Merkmale der Variable signifikant von einer spezifizierten Erwartung oder Hypothese abweichen.

Die univariate Analyse dient als entscheidender Vorläuferschritt, bevor komplexe multivariate Analysen durchgeführt werden. Sie hilft Analysten dabei, Ausreißer zu identifizieren, die Datenqualität zu verstehen und erste Hypothesen über die Daten zu bilden. Dieser Prozess ist in verschiedenen Bereichen von großer Bedeutung, einschließlich Finanzen, Gesundheitswesen, Marketing und Sozialwissenschaften, in denen datengesteuerte Entscheidungsfindung auf einem tiefen Verständnis einzelner Variablen basiert, bevor deren Wechselwirkungen erkundet werden.

Was sind die verschiedenen Datentypen und warum sind sie für die Datenanalyse wichtig?

Bei der univariaten Analyse werden einzelne Variablen innerhalb eines Datensatzes untersucht, um deren Merkmale und Verteilung zu verstehen. Die Art der Daten, mit denen Du zu tun hast, spielt eine entscheidende Rolle bei der Gestaltung der Methoden und Techniken, die bei dieser Analyse verwendet werden. Es gibt zwei primäre Datentypen: numerisch (quantitativ) und kategorisch (qualitativ), die jeweils ihre Bedeutung in der univariaten Analyse haben.

1. Numerische Daten (Quantitativ):

• Kontinuierliche Daten: Kontinuierliche numerische Daten können jeden Wert innerhalb eines Bereichs annehmen. Beispiele sind Alter, Einkommen, Temperatur und Körpergröße. In der univariaten Analyse hilft dir das Verständnis der zentralen Tendenz (Mittelwert, Median) und der Streuung (Varianz, Standardabweichung) kontinuierlicher Daten dabei, die Variabilität und Verteilung der Daten zu erfassen.
• Diskrete Daten: Diskrete numerische Daten bestehen aus getrennten, separaten Werten. Beispiele sind die Anzahl der Kinder in einer Familie, die Anzahl der Kundenbeschwerden oder die Anzahl der verkauften Produkte. In der univariaten Analyse für diskrete Daten geht es oft darum, die Anzahl, Proportionen oder Prozentsätze bestimmter Werte zu berechnen.
• Bedeutung: Numerische Daten liefern wichtige Einblicke in die Größe, Variation und Muster innerhalb einer Variable. Die univariate Analyse hilft dabei, die statistischen Eigenschaften der Daten aufzudecken, Ausreißer zu identifizieren und deren Verteilung zu verstehen. Sie bildet die Grundlage für fortgeschrittenere statistische Techniken.

2. Kategoriale Daten (Qualitativ):

• Nominaldaten: Nominalkategoriale Daten repräsentieren Kategorien ohne inhärente Reihenfolge oder Rangfolge. Beispiele sind Geschlecht, Familienstand oder Arten von Obst. In der univariaten Analyse für nominale Daten liegt der Fokus auf der Berechnung von Häufigkeiten und Anteilen für jede Kategorie.
• Ordinaldaten: Ordinalkategoriale Daten verfügen über Kategorien mit einer sinnvollen Reihenfolge oder Rangfolge, aber die Intervalle zwischen ihnen sind nicht gleichmäßig. Beispiele sind Bildungsniveaus (z. B. Abitur, Bachelor, Master) oder Kundenzufriedenheitsbewertungen (z. B. niedrig, mittel, hoch). In der univariaten Analyse für ordinale Daten berücksichtigt man die Rangfolge und kann Mediane oder Modalwerte berechnen.
• Bedeutung: Kategoriale Daten liefern wertvolle Informationen über Gruppen, Klassen oder Kategorien. Die univariate Analyse hilft dabei, die Verteilung dieser Kategorien und die Häufigkeit jeder einzelnen aufzudecken. Das Verständnis der Verteilung kategorialer Daten ist entscheidend für fundierte Entscheidungen, die Segmentierung von Daten und die Identifizierung von Mustern.

Warum Datentypen in der univariaten Analyse wichtig sind:

• Angemessene Zusammenfassung: Die Wahl von Zusammenfassungsstatistiken, Diagrammen und Visualisierungstechniken hängt vom Datentyp ab. Für numerische Daten kannst du Histogramme oder Boxplots verwenden, während Balkendiagramme oder Kreisdiagramme für kategoriale Daten geeigneter sind.
• Statistische Tests: Unterschiedliche Datentypen erfordern unterschiedliche statistische Tests. Für numerische Daten könntest du Tests wie t-Tests oder ANOVA durchführen, während für kategoriale Daten Chi-Quadrat-Tests oder Kontingenztafeln verwendet werden.
• Daten-Transformation: Der Datentyp beeinflusst, ob Daten-Transformationsmethoden wie Normalisierung oder Skalierung erforderlich sind. Numerische Daten erfordern möglicherweise diese Transformationen für die Modellierung, während kategoriale Daten die Codierung oder die Erstellung von Dummy-Variablen erfordern könnten.
• Verständnis der Daten: Der Datentyp liefert Einblicke in die Natur der Variable. Handelt es sich um kontinuierliche Daten, die auf einen allmählichen Fortschritt hinweisen, oder um kategoriale Daten, die verschiedene Kategorien oder Gruppen darstellen? Dieses Verständnis ist entscheidend für eine sinnvolle Interpretation.

Zusammenfassend ist die Anerkennung und Unterscheidung zwischen numerischen und kategorialen Daten in der univariaten Analyse von grundlegender Bedeutung. Jeder Datentyp erfordert maßgeschneiderte Ansätze, um seine einzigartigen Eigenschaften und Verteilungen aufzudecken, was den Weg für tiefere Einblicke und fundierte Entscheidungsfindung ebnet.

Was ist deskriptive Statistik?

Deskriptive Statistiken sind ein Zweig der Statistik, der sich darauf konzentriert, Daten in einer sinnvollen und informativen Weise zusammenzufassen und darzustellen. Sie bieten Werkzeuge und Techniken zur Analyse einzelner Variablen (univariate Analyse) und zum Verständnis der zentralen Tendenzen, Variationen und Verteilungen dieser Variablen.

Die Verbindung zwischen deskriptiven Statistiken und univariater Analyse ist intrinsisch, da beide grundlegende Schritte im Prozess der explorativen Datenanalyse (EDA) sind. Hier sind einige Gründe, warum die univariate Analyse und die deskriptive Statistik eng miteinander verbunden sind:

• Zusammenfassung der Daten: Deskriptive Statistiken helfen dir dabei, die wesentlichen Merkmale einer einzelnen Variable zusammenzufassen. Die univariate Analyse hingegen beinhaltet das Erforschen und Untersuchen einer Variable nach der anderen, um deren Eigenschaften zu verstehen.
• Zentrale Tendenz: Deskriptive Statistiken liefern Maße der zentralen Tendenz wie den Mittelwert, den Median und den Modus. Diese Maße sind wesentliche Bestandteile der univariaten Analyse und helfen dir dabei, den typischen oder zentralen Wert innerhalb der Daten zu identifizieren.
• Variabilität: Deskriptive Statistiken bieten Einblicke in die Variabilität oder Streuung der Daten, oft durch Kennzahlen wie Varianz, Standardabweichung und Spannweite. Die univariate Analyse beinhaltet die Bewertung, wie sich Datenpunkte von der zentralen Tendenz abweichen, um dir ein Gefühl für die Datenverteilung zu vermitteln.
• Datenverteilung: Deskriptive Statistiken geben auch Informationen über die Datenverteilung preis. Das Verständnis, ob Daten einer Normalverteilung folgen oder Schiefe oder Kurtosis aufweisen, ist in der univariaten Analyse wichtig, um fundierte Entscheidungen über Datenmodellierung und Analysetechniken zu treffen.
• Visualisierung: Deskriptive Statistiken werden durch verschiedene Datenvisualisierungstechniken wie Histogramme, Boxplots und Dichtediagramme ergänzt, die integraler Bestandteil der univariaten Analyse sind. Visualisierungen helfen dir, Einblicke in Datenmuster und Verteilungen zu gewinnen.
• Datenbereinigung: In der deskriptiven Statistik und der univariaten Analyse ist die Identifizierung und Behandlung von Ausreißern, fehlenden Werten oder Datenanomalien entscheidend, um die Genauigkeit und Zuverlässigkeit der Ergebnisse sicherzustellen.
• Dateninterpretation: Deskriptive Statistiken bilden die Grundlage für die Interpretation der Ergebnisse der univariaten Analyse. Wenn du beispielsweise den Mittelwert und die Standardabweichung einer Variable berechnest, ermöglicht dir die univariate Analyse, zu untersuchen, wie einzelne Datenpunkte zu diesen Zusammenfassungsstatistiken in Beziehung stehen.
• Vergleich: Deskriptive Statistiken können verwendet werden, um verschiedene univariate Datensätze miteinander zu vergleichen. Durch die Zusammenfassung der Merkmale jedes Datensatzes kannst du fundierte Vergleiche anstellen und sinnvolle Schlussfolgerungen ziehen.

Zusammenfassend gehen deskriptive Statistiken und univariate Analyse in den ersten Stadien der Datenexploration Hand in Hand. Deskriptive Statistiken rüsten dich mit den Werkzeugen aus, um einzelne Variablen zusammenzufassen und zu verstehen, während die univariate Analyse es dir ermöglicht, deine Exploration zu vertiefen, indem du die Eigenschaften, die Verteilung und die Beziehungen einer Variablen untersuchst, um ein umfassendes Verständnis deiner Daten zu erlangen. Gemeinsam legen diese Techniken den Grundstein für fortgeschrittenere statistische Analysen und datengesteuerte Entscheidungsfindung.

Was sind die verschiedenen Maße der zentralen Tendenz?

Maße der zentralen Tendenz in der univariaten Analyse

Bei der univariaten Analyse ist das Verständnis der zentralen Tendenz der Daten von grundlegender Bedeutung. Maße der zentralen Tendenz geben Aufschluss darüber, wo sich die meisten Datenpunkte gruppieren, und helfen Dir, den typischen oder zentralen Wert eines Datensatzes zu erfassen. Hier sind die wichtigsten Maße:

Mittelwert (Durchschnitt):

• Der Mittelwert ist die Summe aller Datenpunkte geteilt durch die Anzahl der Datenpunkte.
• Er ist empfindlich gegenüber Extremwerten (Ausreißern) und eignet sich für normal verteilte Daten.
• Berechnet als:

\(\) \[ \text{Mean} = \frac{\sum_{i=1}^{n} x_i}{n} \]

Median:

• Der Median ist der mittlere Wert in einem Datensatz, der in auf- oder absteigender Reihenfolge angeordnet ist.
• Er wird weniger von Ausreißern beeinflusst und eignet sich daher für schiefe Daten.
• Bei Datensätzen mit einer geraden Anzahl von Beobachtungen ist der Median der Durchschnitt der beiden mittleren Werte.

Modus:

• Der Modus ist der am häufigsten vorkommende Wert in einem Datensatz.
• Er ist ideal für kategoriale oder diskrete Daten, kann aber auch für kontinuierliche Daten verwendet werden.
• Ein Datensatz kann einen Modus (unimodal), mehrere Modi (multimodal) oder keinen Modus aufweisen.
• Jedes dieser Maße bietet einzigartige Einblicke in die zentralen Tendenzen der Daten. Ziehe bei der Datenanalyse die Verwendung aller drei Maße in Betracht, um ein umfassendes Verständnis für die Verteilung und die Merkmale Ihres Datensatzes zu entwickeln.

Was sind die Herausforderungen und Grenzen der univariaten Analyse?

Die univariate Analyse, d. h. die isolierte Untersuchung einzelner Variablen, ist ein grundlegender Ansatz für die Datenerforschung und -analyse. Es ist jedoch wichtig, die ihr innewohnenden Einschränkungen und Herausforderungen zu erkennen. Das Verständnis dieser Einschränkungen kann Datenanalysten und Forschern helfen, fundiertere Entscheidungen bei der Auswahl von Analysemethoden und der Interpretation von Ergebnissen zu treffen.

Eine der wichtigsten Einschränkungen der univariaten Analyse ist ihr begrenzter Kontext. Dieser Ansatz konzentriert sich ausschließlich auf eine einzelne Variable und bietet Einblicke in das Verhalten dieser Variable, aber oft keine ganzheitliche Sicht auf komplexe Phänomene. In Situationen, in denen mehrere Variablen interagieren und sich gegenseitig beeinflussen

Eine weitere Herausforderung ist das Potenzial für eine zu starke Vereinfachung. Die univariate Analyse vereinfacht die Beziehungen, indem sie Wechselwirkungen zwischen den Variablen nicht berücksichtigt. In der Realität interagieren die Variablen oft auf komplizierte Weise, und ihre kombinierten Auswirkungen können durch eine univariate Untersuchung allein nicht angemessen erfasst werden. Dies kann zu einer verzerrten oder übermäßig vereinfachten Darstellung komplexer Systeme führen.

Darüber hinaus ist die univariate Analyse nur begrenzt in der Lage, einen Kausalzusammenhang herzustellen. Sie kann zwar Korrelationen zwischen Variablen aufzeigen, aber keine Kausalität feststellen. Korrelation impliziert keine Kausalität, und die Feststellung kausaler Beziehungen erfordert in der Regel weitere Experimente, Kausalanalysen oder kontrollierte Studien.

Die Datenqualität ist ein entscheidender Faktor, der die Wirksamkeit der univariaten Analyse beeinflusst. Ausreißer, Anomalien oder fehlende Werte in den Daten können die Ergebnisse und Interpretationen der univariaten Analyse erheblich beeinträchtigen. Daher ist eine gründliche Datenvorverarbeitung erforderlich, um die Qualität und Integrität der Daten zu gewährleisten.

Eine weitere Überlegung betrifft die Annahme der Datenverteilung. Bei der univariaten Analyse wird häufig davon ausgegangen, dass die Daten einer bestimmten Verteilung folgen, z. B. einer Normalverteilung. Reale Daten können jedoch erheblich von diesen Annahmen abweichen, was zu unzuverlässigen Ergebnissen führt, wenn univariate Verfahren angewendet werden.

Die univariate Analyse ist von Natur aus nur begrenzt geeignet, multivariate Erkenntnisse zu liefern. Sie konzentriert sich ausschließlich auf einzelne Variablen und gibt keinen Aufschluss darüber, wie die Variablen zueinander in Beziehung stehen. Für ein umfassenderes Verständnis komplexer Zusammenhänge sind multivariate Analyseverfahren erforderlich, die die Wechselwirkungen zwischen den Variablen berücksichtigen.

Außerdem eignet sich die univariate Analyse möglicherweise nicht für die Vorhersagemodellierung in Fällen, in denen mehrere Faktoren die Ergebnisse beeinflussen. Sie kann zwar das Verhalten einzelner Variablen aufdecken, greift aber oft zu kurz, wenn es um die Vorhersage von Ergebnissen geht, die durch komplexe Wechselwirkungen zwischen Variablen beeinflusst werden.

Die Stichprobengröße ist ein weiterer Aspekt. Die Wirksamkeit der univariaten Analyse kann durch den Umfang der Stichprobe beeinflusst werden. Kleine Stichproben liefern möglicherweise keine statistisch aussagekräftigen Ergebnisse und schränken den Umfang und die Zuverlässigkeit der Analyse ein.

Zeitliche Aspekte werden bei der univariaten Analyse oft übersehen. Sie kann zeitliche Trends oder saisonale Muster in Zeitreihendaten oder Daten mit einer zeitlichen Komponente nicht angemessen erfassen. Um die zeitliche Dynamik zu verstehen, sind spezielle Techniken der Zeitreihenanalyse erforderlich.

Schließlich geht die univariate Analyse nicht auf Veränderungen oder Trends im Zeitverlauf ein. Um zu verstehen, wie sich die Variablen im Laufe der Zeit entwickeln, sind Zeitreihenanalysen oder fortgeschrittenere Methoden erforderlich.

Zusammenfassend lässt sich sagen, dass die univariate Analyse zwar einen wertvollen ersten Schritt in der Datenerforschung darstellt, aber nicht ohne Einschränkungen ist. Das Erkennen dieser Grenzen ist für eine fundierte Entscheidungsfindung darüber, wann univariate Techniken eingesetzt werden sollen und wann zu multivariaten Methoden übergegangen werden soll, die komplexe Wechselwirkungen zwischen Variablen berücksichtigen, unerlässlich.

Wie kannst Du eine univariate Analyse in Python umsetzen?

Python ist eine vielseitige und weit verbreitete Programmiersprache im Bereich der Datenanalyse und bietet ein reichhaltiges Ökosystem an Bibliotheken und Werkzeugen, um univariate Analysen effektiv durchzuführen. Hier findest Du eine schrittweise Anleitung, wie Du Python für univariate Analysen verwendest:

1. Datenerfassung:

• Beginne mit dem Importieren Deiner Daten in eine Python-Umgebung. Beliebte Bibliotheken für die Datenverarbeitung sind Pandas und NumPy. Du kannst Daten aus verschiedenen Quellen einlesen, z. B. aus CSV-Dateien, Excel-Arbeitsblättern oder Datenbanken.

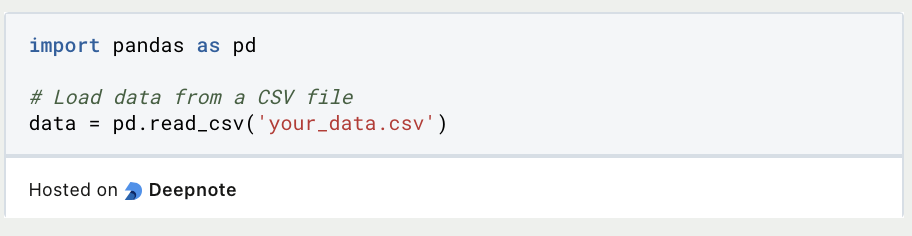
2. Datenexploration:

• Beginne mit der Erkundung Deiner Daten mit Pandas. Verwende Funktionen wie head(), describe() und info(), um einen ersten Überblick über Deinen Datensatz zu erhalten. Diese Funktionen liefern Informationen über Datentypen, fehlende Werte und grundlegende Statistiken.

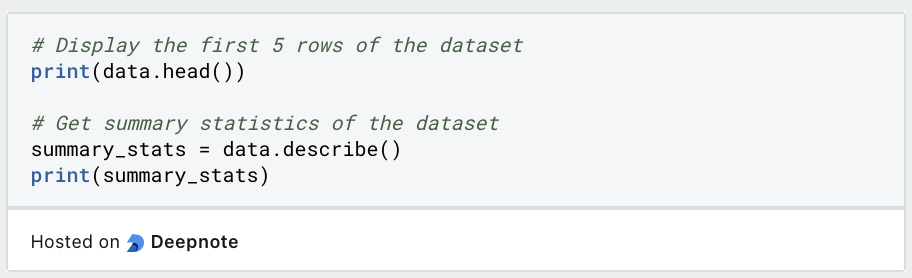
3. Datenvisualisierung:

• Die Visualisierung ist ein wichtiger Aspekt der univariaten Analyse. Python bietet mehrere Bibliotheken zur Erstellung informativer Diagramme und Grafiken.
• Verwende Matplotlib für die Erstellung statischer, stark anpassbarer Diagramme. Für interaktive und visuell ansprechende Visualisierungen kannst Du Bibliotheken wie Seaborn und Plotly verwenden.
• Zu den gängigen univariaten Diagrammen gehören Histogramme, Boxplots, Balkendiagramme und Dichteplots. Diese helfen Dir, die Verteilung und die Merkmale einzelner Variablen zu visualisieren.

4. Deskriptive Statistik:

• Python-Bibliotheken wie Pandas bieten Funktionen zur Berechnung von deskriptiven Statistiken für Deine Variablen. Verwende mean(), median(), std() und var(), um zentrale Tendenzen und Streuungsmaße zu berechnen.

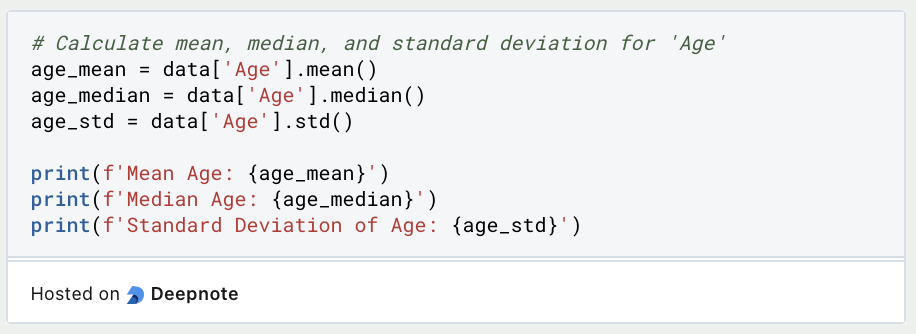
5. Umgang mit fehlenden Werten:

• Behebe fehlende Daten mit Pandas-Funktionen wie dropna() oder fillna(). Ziehe Strategien wie Mittelwert-Imputation oder Interpolation je nach Art Deiner Daten in Betracht.

6. Ausreißererkennung:

• Identifiziere und behandle Ausreißer mit Python-Bibliotheken wie Scipy oder speziellen Bibliotheken wie PyOD. Visualisierungen wie Box-Plots und Streudiagramme können ebenfalls bei der Erkennung von Ausreißern helfen.

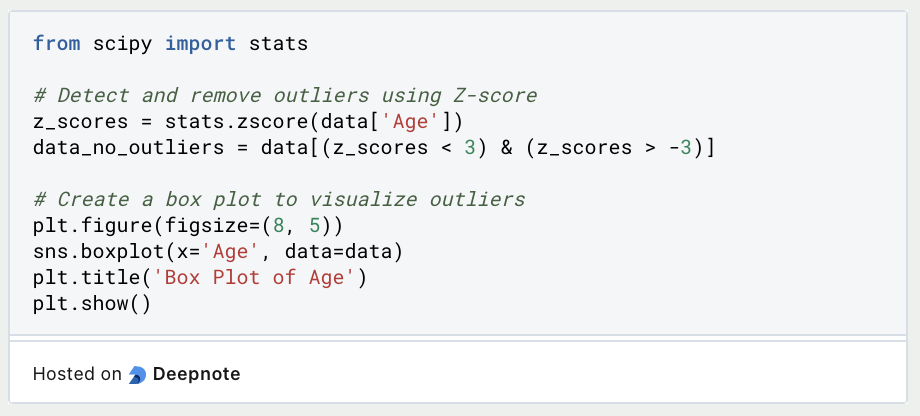
7. Datentransformation:

• Je nach Deiner Analyse musst Du Deine Daten möglicherweise transformieren. Zu den üblichen Transformationen gehören logarithmische Transformationen, Standardisierung (Skalierung) oder Normalisierung. Bibliotheken wie Scikit-Learn bieten zu diesem Zweck Vorverarbeitungswerkzeuge.

8. Statistische Tests:

• Führe statistische Tests durch, um Hypothesen über Deine Daten zu überprüfen. Die Scipy-Bibliothek von Python enthält eine breite Palette statistischer Tests, darunter t-Tests, ANOVA, Chi-Quadrat-Tests und mehr. Diese Tests helfen Dir, Rückschlüsse auf Deine Daten zu ziehen und Schlussfolgerungen zu ziehen.

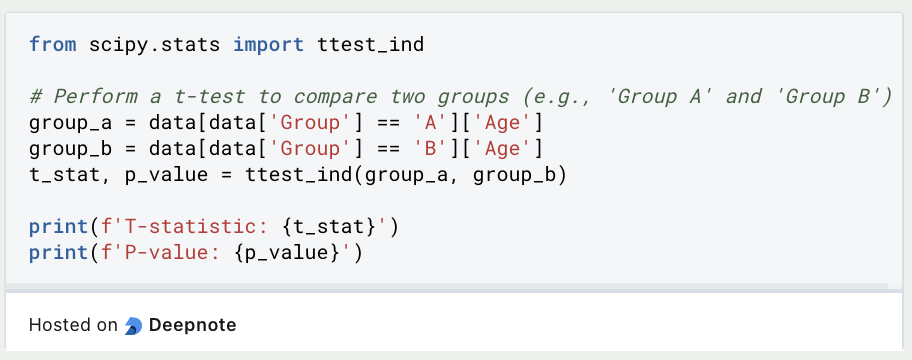
Zusammenfassend lässt sich sagen, dass die Verwendung von Python für univariate Analysen Dich in die Lage versetzt, effizient und effektiv aussagekräftige Erkenntnisse aus Deine Daten zu gewinnen. Diese schrittweise Anleitung hat Dir gezeigt, wie Du verschiedene Python-Bibliotheken und -Werkzeuge einsetzen kannst, um Aufgaben wie Datenerfassung, Exploration, Visualisierung, deskriptive Statistik, Umgang mit fehlenden Werten, Ausreißererkennung, Datentransformation, statistische Tests, Dateninterpretation, Dokumentation und fortgeschrittene Analyse durchzuführen.

Das solltest Du mitnehmen

• Die univariate Analyse ist ein grundlegender Schritt in der Datenanalyse und konzentriert sich auf das Verständnis einzelner Variablen.
• Sie bietet Einblicke in die Datenverteilung, zentrale Tendenzen, Variabilitäten und grundlegende Statistiken.
• Verschiedene Datentypen (numerisch, kategorisch) erfordern spezifische Techniken zur Analyse und Visualisierung.
• Deskriptive Statistiken und Datenvisualisierungen (Histogramme, Boxplots usw.) spielen bei der univariaten Analyse eine entscheidende Rolle.
• Python bietet eine vielseitige Umgebung für die effiziente Durchführung univariater Analyseaufgaben.
• Bibliotheken wie Pandas, Matplotlib, Seaborn und Scipy sind wertvolle Werkzeuge in Python für univariate Analysen.
• Der Umgang mit fehlenden Daten, die Erkennung von Ausreißern und die Datentransformation sind wesentliche Schritte der Datenvorverarbeitung.
• Die univariate Analyse stattet Datenanalysten mit den grundlegenden Fähigkeiten aus, die sie benötigen, um Erkenntnisse zu gewinnen, Anomalien zu erkennen und Daten für weitergehende Analysen vorzubereiten. Dies ist ein entscheidender Schritt im Datenanalyseprozess, der es Ihnen ermöglicht, einzelne Variablen zu verstehen, bevor Sie sich in multivariate Beziehungen vertiefen.

Andere Beiträge zum Thema univariate Analyse

IBM hat einen interessanten Artikel zum Thema General Linear Model Univariate Analysis verfasst, den Du hier finden kannst.