Die logistische Regression ist eine spezielle Form der Regressionsanalyse, die genutzt wird, wenn die abhängige, also die vorherzusagende, Variable, nur eine bestimmte Anzahl an möglichen Werten annehmen kann. Man spricht dann auch davon, dass diese Variable nominal- bzw. ordinalskaliert ist. Die logistische Regression liefert uns als Ergebnis eine Wahrscheinlichkeit mit der der Datensatz einer Klasse zuzuordnen ist.

Bei welchen Fragestellungen kann man die logistische Regression nutzen?

In Anwendungsfällen kommt es tatsächlich sehr häufig vor, dass wir nicht einen konkreten Zahlenwert vorhersagen wollen, sondern lediglich bestimmen, in welche Klasse oder welchen Bereich ein Datensatz fällt. Hier mal ein paar klassische, praktische Beispiele für die man die logistische Regression nutzen kann:

• Politik: Welche der möglichen fünf Parteien wird eine Person wählen, wenn nächsten Sonntag Wahlen wären?
• Medizin: Ist eine Person “anfällig” oder “nicht anfällig” für eine bestimmte Krankheit abhängig von einigen medizinischen Parametern der Person?
• Betriebswirtschaft: Wie hoch ist die Wahrscheinlichkeit, dass ein bestimmtes Produkt gekauft wird abhängig von Alter, Wohnort und Beruf einer Person?

Wie funktioniert die logistische Regression?

Bei der linearen Regression haben wir versucht einen konkreten Wert für die abhängige Variable vorherzusagen, statt eine Wahrscheinlichkeit auszurechnen, mit der die Variable einer bestimmten Klasse angehört. Beispielsweise haben wir versucht die konkrete Klausurnote eines Studenten zu bestimmen, abhängig von den Stunden, die der Student für das Fach gelernt hat. Die Grundlage für die Schätzung des Modells ist die Regressionsgleichung und entsprechend auch der Graph, der sich daraus ergibt.

Ein Beispiel: Wir wollen ein Modell aufbauen, das uns die Wahrscheinlichkeit vorhersagt, dass eine Person ein E-Bike kauft, abhängig von ihrem Alter. Nachdem wir ein paar Probanden befragt haben, erhalten wir folgendes Bild:

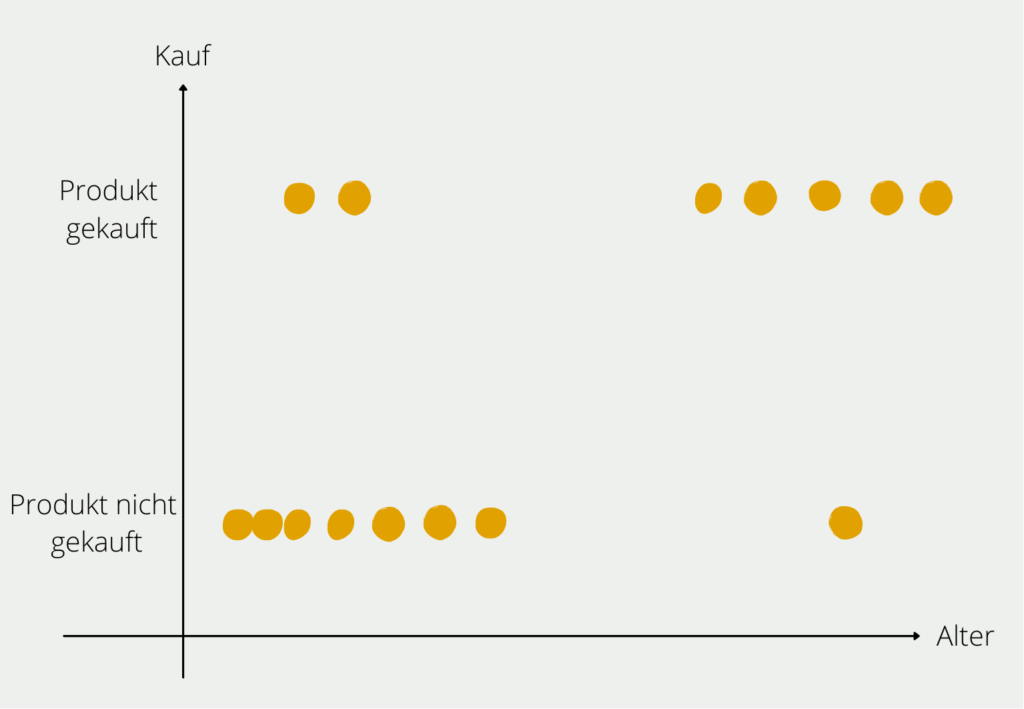
Aus unserer kleinen Probandengruppe können wir die Verteilung erkennen, dass junge Personen größtenteils kein E-Bike gekauft haben (unten links im Diagramm) und vor allem ältere Menschen sich ein E-Bike kaufen (oben rechts im Diagramm). Natürlich gibt es in beiden Altersschichten auch Ausreißer, aber der Großteil der Befragten entspricht der Regel, dass mit steigendem Alter die Wahrscheinlichkeit wächst, dass man sich ein E-Bike zulegt. Diese Regel, die wir in den Daten erkannt haben, wollen wir nun auch mathematisch belegen.

Dazu müssen wir eine Funktion finden, die möglichst nahe an der Punkteverteilung, die wir im Diagramm sehen, liegt und zusätzlich nur Werte zwischen 0 und 1 annimmt. Somit fällt eine lineare Funktion, wie wir sie bei der linearen Regression genutzt haben bereits raus, da diese im Bereich zwischen -∞ und +∞ liegt. Jedoch gibt es eine andere mathematische Funktion, die unseren Anforderungen entspricht: die Sigmoid Funktion.

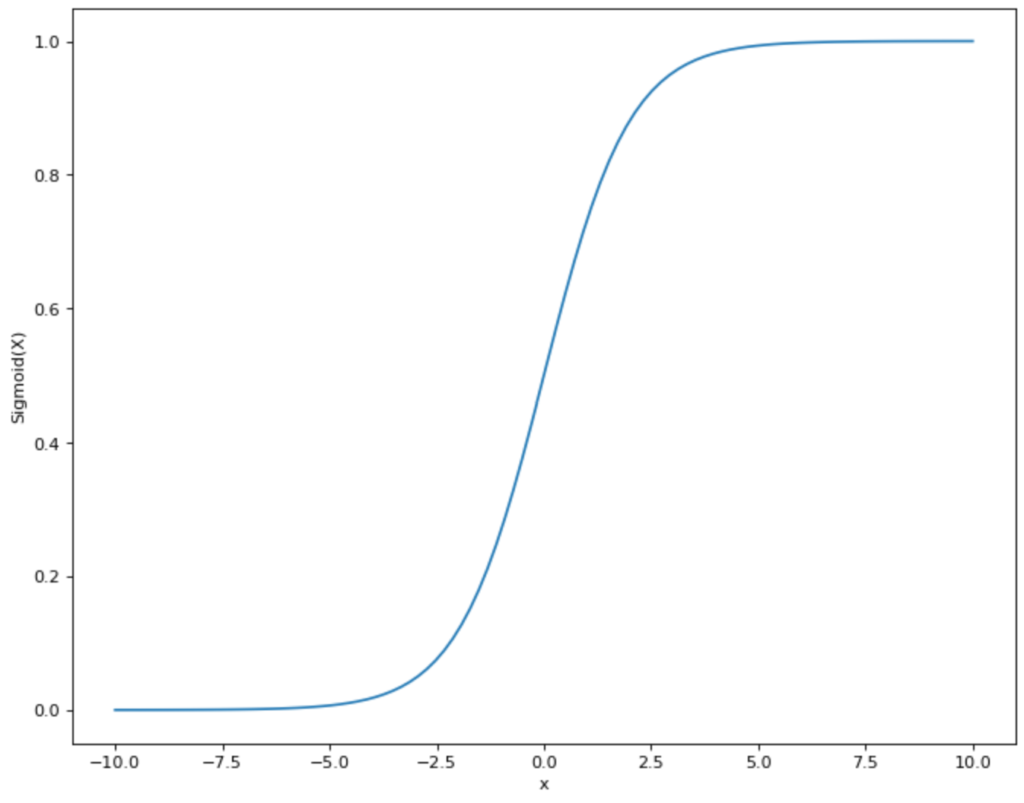
Die Funktionsgleichung des Sigmoid Graphen sieht folgendermaßen aus:

\(\) \[S(x) = \frac{1}{1+e^{-x}}\]

Oder für unser Beispiel:

\(\) \[P(\text{Kauf E-Bike})) = \frac{1}{1+e^{-(a + b_1 \cdot \text{Alter})}}\]

Damit haben wir eine Funktion, die uns als Ergebnis die Wahrscheinlichkeit des E-Bike Kaufs liefert und als Variable das Alter der Person nutzt. Der Graph würde dann für unser Beispiel in etwa so aussehen:

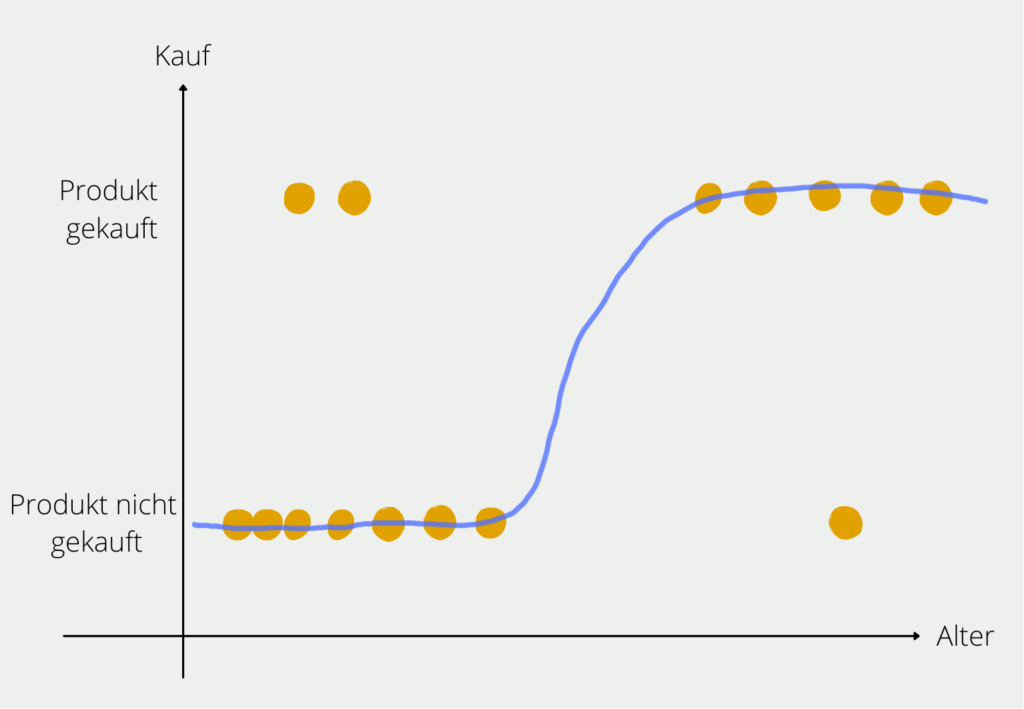
In der Praxis sieht man häufig nicht die Schreibweise, die wir genutzt haben. Stattdessen stellt man die Funktion so um, dass die eigentliche Regressionsgleichung deutlich wird:

\(\) \[logit(P(\text{Kauf E-Bike}) = a + b_1 \cdot \text{Alter}\]

Wie lässt sich die logistische Regression interpretieren?

Die Zusammenhänge zwischen unabhängiger und abhängiger Variable, die man bei einer logistischen Regression bekommt, sind nicht linear und können somit auch nicht so einfach interpretiert werden, wie bei einer linearen Regression.

Eine grundlegende Interpretation ist trotzdem möglich. Wenn der Koeffizient vor der unabhängigen Variable (Alter) positiv ist, dann steigt auch mit Zunahme der Variable die Wahrscheinlichkeit der Sigmoid Funktion. In unserem Fall bedeutet das, dass wenn b1 positiv ist, mit zunehmendem Alter auch die Wahrscheinlichkeit des E-Bike Kaufs zunimmt. Das Gegenteil trifft natürlich auch zu, also bei positivem b1, sinkt auch die Wahrscheinlichkeit des E-Bike Kaufs mit abnehmendem Alter.

Darüber hinaus sind verständliche Interpretationen mit einer logistischen Regression nur sehr schwierig möglich. In vielen Fällen berechnet man die sogenannte Odds Ratio, also das Verhältnis aus der Wahrscheinlichkeit des Eintritts und der Wahrscheinlichkeit des Nicht-Eintritts:

\(\) \[odds = \frac{p}{1-p}\]

Wenn man zusätzlich den Logarithmus aus diesem Bruch bildet, erhält man den sogenannten Logit:

\(\) \[z = Logit = \ln (\frac{p}{1-p})\]

Das sieht verwirrend aus. Widmen wir uns wieder unserem Beispiel, um hier mehr Klarheit reinzubringen. Angenommen für unser Beispiel erhalten wir die folgende logistische Regressionsgleichung:

\(\) \[logit(P(\text{Kauf E-Bike})) = 0.2 + 0.05 \cdot \text{Alter}\]

Diese Funktion können wir erstmal linear interpretieren, also ein Jahr erhöht den logit(p) um 0.05. Der logit(p) ist nach unserer Definition nichts anderes als ln(p/(1-p)). Wenn sich also ln(p/(1-p)), um 0.05 erhöht, dann erhöht sich p/(1-p), um exp(0.05) (Merke: Der Logarithmus ln und die e-Funktion (exp) lösen sich gegenseitig auf). Mit jedem Jahr, das man älter wird, erhöht sich also die Chance (nicht Wahrscheinlichkeit!) ein E-Bike zu kaufen um exp(0.05) = 1.051, also um 5.1 Prozent.

Wie kann man die logistische Regression bewerten?

Die logistische Regression ist eine weit verbreitete statistische Methode für binäre Klassifizierungsprobleme, bei denen das Ziel darin besteht, die Wahrscheinlichkeit des Eintretens eines Ereignisses (z. B. ob ein Kunde ein Produkt kauft oder nicht) auf der Grundlage einer Reihe von Eingangsmerkmalen vorherzusagen. Um die Leistung eines logistischen Regressionsmodells zu bewerten, können verschiedene Metriken verwendet werden.

• Konfusionsmatrix: Eine Konfusionsmatrix ist eine Tabelle, die die Leistung eines binären Klassifikationsmodells zusammenfasst. Sie zeigt die Anzahl der wahren Positiven (TP), falschen Positiven (FP), wahren Negativen (TN) und falschen Negativen (FN) in tabellarischer Form.
• Genauigkeit: Die Genauigkeit ist die am häufigsten verwendete Metrik zur Bewertung der Leistung eines logistischen Regressionsmodells. Sie ist definiert als das Verhältnis zwischen der Anzahl der richtigen Vorhersagen und der Gesamtzahl der Vorhersagen. Die Genauigkeit kann jedoch irreführend sein, wenn die Klassen unausgewogen sind.
• Precision: Die Präzision ist das Verhältnis zwischen der Zahl der richtigen positiven Vorhersagen und der Gesamtzahl der positiven Vorhersagen (d. h. richtige positive Vorhersagen plus falsch positive Vorhersagen). Sie misst den Anteil der positiven Vorhersagen, die tatsächlich richtig sind.
• Recall: Der Recall ist das Verhältnis zwischen der Anzahl wahrer positiver Vorhersagen und der Gesamtzahl tatsächlich positiver Vorhersagen (d. h. wahrer positiver Vorhersagen plus falscher negativer Vorhersagen). Sie misst den Anteil der tatsächlich positiven Instanzen, die korrekt vorhergesagt wurden.
• F1-Score: Der F1-Score ist das harmonische Mittel aus Precision und Recall. Es handelt sich um eine einzige Metrik, die sowohl Präzision als auch Recall kombiniert und ein ausgewogenes Maß für beide darstellt.
• ROC-Kurve: Die ROC-Kurve (Receiver Operating Characteristic) ist eine grafische Darstellung der Leistung eines binären Klassifikationsmodells bei verschiedenen Klassifikationsschwellenwerten. Sie stellt die wahr-positive Rate (TPR) gegen die falsch-positive Rate (FPR) für verschiedene Schwellenwerte dar.
• AUC-Wert: Der Bereich unter der ROC-Kurve (AUC) ist ein skalarer Wert, der die Leistung eines binären Klassifikationsmodells über alle Klassifikationsschwellenwerte hinweg zusammenfasst. Er bietet ein aggregiertes Maß für die Fähigkeit des Modells, zwischen positiven und negativen Instanzen zu unterscheiden.

Zusammenfassend lässt sich sagen, dass die Bewertung eines logistischen Regressionsmodells die Verwendung mehrerer Metriken beinhaltet, von denen jede eine andere Perspektive auf die Leistung des Modells bietet. Die Wahl der Metriken hängt von den spezifischen Anforderungen der Anwendung und dem Kompromiss zwischen Präzision und Recall ab.

Wie kann man mit unausgeglichenen Daten um?

Der Umgang mit unausgewogenen Daten ist eine häufige Herausforderung beim maschinellen Lernen, die insbesondere bei der Arbeit mit logistischen Regressionsmodellen relevant ist. In vielen realen Szenarien kann eine der interessierenden Klassen in den Daten unterrepräsentiert sein, was zu einem verzerrten Modell führt, das bei dieser Klasse schlecht abschneidet.

Es gibt mehrere Techniken zur Behandlung unausgewogener Daten bei der Arbeit mit logistischen Regressionsmodellen:

• Resampling: Dabei wird entweder ein Oversampling der Minderheitenklasse oder ein Undersampling der Mehrheitsklasse durchgeführt, um den Datensatz auszugleichen. Dieser Ansatz kann jedoch zu einer Überanpassung oder zum Verlust wichtiger Informationen führen.
• Kostensensitives Lernen: Hierbei werden der Fehlklassifizierung verschiedener Klassen unterschiedliche Kosten zugewiesen. Indem die Kosten für die Fehlklassifizierung der Minderheitenklasse erhöht werden, wird das Modell ermutigt, die korrekte Klassifizierung dieser Klasse zu bevorzugen.
• Ensemble-Methoden: Ensemble-Methoden wie Bagging, Boosting oder Stacking können für den Umgang mit unausgewogenen Daten effektiv sein. Bei diesen Methoden werden mehrere logistische Regressionsmodelle kombiniert, um die Gesamtleistung des Modells zu verbessern.
• Synthetische Datengenerierung: Dabei werden neue Datenpunkte für die Minderheitenklasse mit Techniken wie SMOTE (Synthetic Minority Over-sampling Technique) erzeugt. Dies kann dazu beitragen, den Datensatz auszugleichen und die Leistung des Modells zu verbessern.
• Auswahl des Algorithmus: In einigen Fällen ist ein logistisches Regressionsmodell möglicherweise nicht der beste Algorithmus für unausgewogene Daten. Andere Algorithmen, wie z. B. Entscheidungsbäume, Random Forest oder Support-Vektor-Maschinen, können bei unausgewogenen Datensätzen besser abschneiden.

Es ist wichtig, die Leistung von logistischen Regressionsmodellen bei unausgewogenen Daten sorgfältig zu bewerten und die geeignete Technik zur Behandlung des Ungleichgewichts zu wählen. Auch die Bewertungsmetriken für unausgewogene Datensätze sollten sorgfältig ausgewählt werden, z. B. die Fläche unter der Receiver-Operating-Characteristic (ROC)-Kurve, die Precision-Recall-Kurve oder der F1-Score.

Das solltest Du mitnehmen

• Die logistische Regression wird genutzt wenn die Ergebnisvariable kategorisch ist.
• Wir nutzen die Sigmoid Funktion als Regressionsgleichung, die nur Werte zwischen 0 und 1 annehmen kann.
• Die logistische Regression und deren Parameter lassen sich nicht so einfach interpretieren, wie die lineare Regression.

Andere Beiträge zum Thema logistische Regression

• Die Universität Zürich hat einen interessanten Beitrag, in dem sie die logistische Regression ausführlich und mit Beispielen erklärt.