What is Fuzzy Logic?

Fuzzy logic is an extension of classical logic and makes it possible to deal with imprecise and uncertain data. Compared to traditional logic, which is based on things being either true or false, fuzzy logic also allows for states in between. This means that states can be “partially true” or “somewhat false”.

In this article, we take a detailed look at fuzzy logic, its concepts, and fundamentals and try to use examples that are as simple as possible. We also show the advantages and disadvantages of using this method and explain how it differs from traditional logic.

Fuzzy logic is an extension of classical Boolean logic which, in addition to the two states true/false or 0/1, also allows statements that are only true or false to a certain degree and therefore assume a value between 0 and 1. This concept was invented in the 1960s by Lotfi Zadeh at the University of California. He tried to solve the problem of teaching a machine to speak human, natural language and discovered that language cannot be classified into 0 and 1.

To be able to represent these vague terms, he invented the concept of fuzzy logic to map uncertainties in a model. Since its introduction, it has become very widespread and is used in a wide variety of applications, such as control engineering or artificial intelligence.

What are Fuzzy Sets and Membership Functions?

To be able to map fuzzy logic, the basic concepts of logic also require some adjustments to function. Fuzzy sets provide a mathematical framework for mapping the uncertainty of fuzzy logic. In contrast to conventional mathematical sets, they enable partial membership. They achieve this by allowing so-called degrees of membership to be set between 0 and 1. A value of 0.7, for example, indicates that a certain element belongs to the set as a percentage of 70%.

This value is determined using the so-called membership function, or fuzzy function. It assigns each element a membership value between 0 and 1, which indicates the degree of membership. In contrast to normal logic, in which a statement can be either true or false, this function enables a gradual classification.

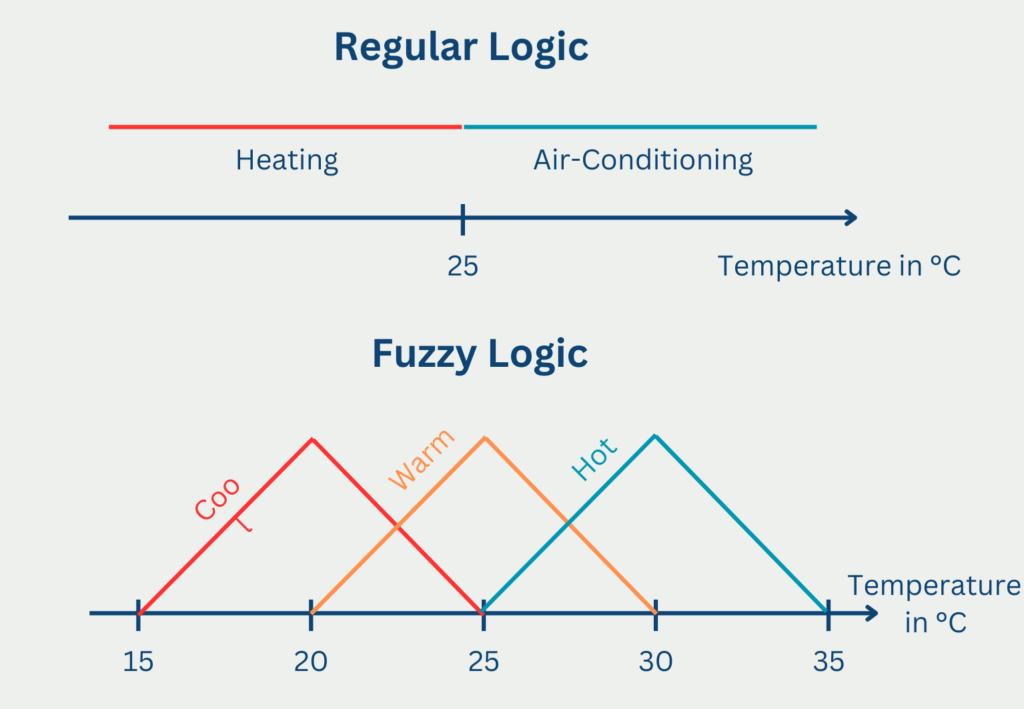
A classic example of this structure is the classification into “warm” or “cold”. In Boolean logic, this could be done by classifying all temperatures below 25°C as “cold” and all above as “warm”. In fuzzy logic, on the other hand, this definition can be made much more flexible, which can then lead to the following membership function, for example:

At 20°C, the membership of the set “warm” is very low at 0.2, so it is only “20% warm”.
At 25°C, on the other hand, the membership value is already 0.7, so it is 70% warm.
At 30°C, the affiliation is 1 and it is therefore completely warm.

This flexible classification option describes reality much more accurately, as we humans perceive temperature in a much more differentiated way than “warm” and “cold”.

What are Fuzzy Operators?

As in classical logic, there are also logical operators in fuzzy logic, such as AND, OR, and NOT. However, these do not behave in the same way with fuzzy sets as with conventional sets, as they work with continuous degrees of membership. In this section, we will take a closer look at the three logical fuzzy operators and give a brief example to explain each of them.

Fuzzy-AND

The fuzzy AND operator describes a conjunction of two or more fuzzy values, which are therefore connected with an AND. The membership value from a conjunction then results from the minimum of the two values:

\(\) \[\mu_{\text{AND}}(A, B) = \min(\mu_A, \mu_B) \]

Here, \(\mu_A\) is the membership value for fuzzy set A, and \(\mu_B\) is the membership value for fuzzy set B. The lower of the two values is used to implement the idea that both conditions must be as true as possible.

Assume an air conditioning system automatically decides whether it should become active. It measures two values, namely whether it is warm and how high the humidity in the room is. Let’s assume that a room has the following values:

“warm”: \(\mu_A = 0.7 \, (70\%)\)
“humid”: \(\mu_B = 0.5 \, (50\%)\)

The fuzzy AND operator now uses the minimum value, i.e. 0.5. Based on this, the air conditioning system now decides that it should run at 50%.

Fuzzy-OR

The fuzzy OR operator is a disjunction of two or more fuzzy values. In contrast to a conjunction, the maximum value is determined from the membership values:

\(\) \[\mu_{\text{OR}}(A, B) = \max(\mu_A, \mu_B) \]

This means that the union of the two fuzzy values is determined by the higher membership value. In Boolean logic, this is similar, as the disjunction becomes true (1) if at least one of the two values is true (1).

If the air conditioner decides based on a disjunction, the example with the previous values could look like this: the air conditioner decides to cool 70% of the time because the air in the room is very humid.

Fuzzy-NOT

The fuzzy NOT operator negates the membership value of an element by subtracting the value from 1. This reflects the fact that if an element has a membership value of 0.8, for example, i.e. 80% of it is true, 20% of it is false.

\(\) \[\mu_{\text{NOT}}(A) = 1 – \mu_A\]

So a room that is 30% warm, i.e. has a membership value of 0.3, has a negated value of 0.7. This is analogous to the statement that a room that is 30% warm is also 70% cold.

T-norms & S-norms

In fuzzy logic, the min function does not necessarily have to be used for conjunction, and the max function for disjunction. Rather, this is just one way of implementing the fuzzy operators, which can also be changed depending on the application.

The T-norms therefore include functions that can be used to model the conjunction. All of these functions have the properties of being monotonically increasing and associative. In most cases, the min function is used for this.

Accordingly, the S-norms include all functions that can be used for a disjunction in fuzzy logic. The most frequently used operator is the max function.

How are decisions made in Fuzzy Logic?

Due to the fuzzy definition of states, decision-making in fuzzy logic is somewhat more complex than in Boolean logic, in which only two states are distinguished. This is why “if-then” formulations play a central role, as they enable decisions to be made based on fuzzy input data.

An exemplary if-then rule in the case of an air conditioning system could then say: “If the temperature is warm and the humidity is high, then set the fan to the medium level”. In this case, the measured values for temperature and humidity are fuzzy, so the decision cannot be based on fixed threshold values, but rather on fluid transitions.

In fuzzy logic, the process of inference describes how a corresponding fuzzy output can be generated based on fuzzy values. In the previous example, the fuzzy inputs of temperature and humidity generate a fuzzy output when setting the fan.

As we have seen, a fuzzy system usually also generates fuzzy outputs. In reality, however, the devices cannot handle these fuzzy instructions. The fan described may not have a “medium” setting and a specific rotational speed should be specified. Therefore, methods are needed that convert fuzzy output into a precise, concrete decision. This method is known as defuzzification.

In many cases, the so-called center of gravity method is used, which uses mathematical calculations to calculate the center of gravity of the fuzzy output as the final value. This defuzzification could then be used in the fan example to calculate the specific increase in speed that needs to be set on the fan.

What are the Applications of Fuzzy Logic?

Fuzzy logic has already established itself in a wide variety of areas, especially when dealing with vague and uncertain values. Due to the given flexibility, significantly more precise and robust decisions can be made. In this section, we present three areas of application in which fuzzy logic has become indispensable.

Automation & Control Technology

Fuzzy logic has become an integral part of control technology, as the examples of air conditioning systems and fans already mentioned make clear. It is also used in washing machines, for example, where attention must be paid to the weight load and the water temperature, which can be very vague. With the help of fuzzy logic, the appliances can make differentiated decisions independently without having to define fixed threshold values.

Artificial Intelligence

In artificial intelligence, the fuzziness often stems from the data sets themselves, for example, because the images in a data set are not entirely clear due to poor lighting or shadows. Fuzzy logic can be used to react to such uncertainties and still make decisions. For example, the outline of a person on surveillance cameras can be very unclear because the lighting is not optimal. Nevertheless, a decision must be made as to whether a person can be recognized with sufficient certainty to trigger an alarm.

Business decisions

In the field of economics, fuzzy logic is used for financial models and risk assessments to take into account uncertainties such as market fluctuations or inaccurate forecasts and still arrive at reliable decisions. Such uncertainties cannot be ruled out when granting loans or making investment decisions, but must not hurt the decision-making process.

The integration of fuzzy logic in different application areas expands the ability of systems to deal with uncertainties and imprecise inputs and still make reliable decisions. In reality, such inaccuracies often cannot be avoided, which is why these systems have great added value.

What are the Advantages and Disadvantages of Fuzzy Logic?

Fuzzy logic offers numerous advantages in various applications if uncertainties and imprecise values are to be included in a decision. However, the limitations should not be ignored, especially in complex systems. This section outlines the most important advantages and disadvantages of fuzzy logic, which should be weighed up before use.

Advantages:

Flexibility: The main undisputed advantage of fuzzy logic is the ability to extend pure Boolean logic with imprecise values. In most realistic applications, such vague states are unavoidable and can only be implemented with great difficulty using the concepts of classical logic. Fuzzy logic, on the other hand, is much more flexible here and allows individual scenarios to be created using the membership function.
User-friendliness: The formulation of rules in the “if-then” format is very intuitive and easy to understand. This makes it possible to map everyday decision-making processes in which decisions are not always based on strict specifications but have to deal with imprecise information.
Robustness: A decision-making system based on fuzzy logic can deal robustly with erroneous data and therefore leads to errors much less frequently than systems based on Boolean logic.

However, such systems also have disadvantages and limitations that should be taken into account when making a choice:

Complexity: with an increase in parameters, a fuzzy system and its rules can quickly become very complex, especially when the number of rules increases. The more rules and parameters are added, the more confusing and complex the overall system becomes, which also significantly increases the computing power required. Maintainability also suffers as a result.
Subjectivity: Due to the high degree of customizability, the choice of membership function is often subjective. This is not a problem in itself, but there is a risk that the performance of the system depends largely on the subjective decisions of the developer. For this reason, a high level of expert knowledge should be available when formulating the rules.

Fuzzy logic is a powerful tool for creating rule-based decision models. However, it can also quickly become highly complex, especially in systems with many parameters. parameters. These points should therefore be considered before making a decision.

What are the Differences between Fuzzy Logic and Regular Logic and other Logic Systems?

Fuzzy logic differs from classical logic systems in many ways. These points are important to be able to evaluate the applicability in specific systems and to make the optimal choice depending on the application.

Comparison with classical logic

Classical or Boolean logic is based on the fact that decisions are binary, i.e. the statements are either true (1) or false (0). Although this has the advantage that decisions are often unambiguous, in reality, this simplification is often too rigid to adequately reflect the complexity.

This difference can be seen in a simple example from control engineering. In Boolean logic, there are only two states, namely switching an air conditioner off or on. In reality, however, the situation is much more complex, as the appliance can be operated in different stages and cool more or less. This complexity can only be mapped as realistically as possible with the help of fuzzy logic.

These differences also become clear in the underlying mathematics of the systems. The AND operator in Boolean logic, for example, is only true if both statements of the conjuncts are true. In fuzzy logic, on the other hand, the so-called T-norm must first be determined, which in many cases is the min function and then returns a vague value.

Comparison with probabilistic logic

Probabilistic systems are based on the probability that a certain result will occur based on the given conditions. These probabilities are objective and are based on data from the past and its analysis. However, this approach differs from fuzzy logic, as the probability does not indicate membership of a set, but merely makes a statement about how systems have behaved in such a situation in the past.

The statement “it will rain 70% of the time tomorrow” therefore has no information content about the degree of affiliation to “rain” or “no rain”, but merely states that it has rained 70% of the time in the past if the external conditions were comparable.

This is what you should take with you

Fuzzy logic differs from Boolean logic in that it allows imprecise values.
Specialized concepts such as fuzzy sets and membership functions are required to map this logic.
Analogous to Boolean logic, fuzzy logic also has the AND, OR, and NOT operators. However, these differ in the underlying functions.
Decision-making in fuzzy logic is carried out using “if-then” formulations, which are intended to imitate human thinking.
With the help of defuzzification, the vague output of fuzzy logic can then be converted back into a real decision value. The center of gravity concept is often used for this purpose.
Fuzzy logic is used in a wide variety of areas, such as control engineering or artificial intelligence.