In the ever-evolving landscape of data science and machine learning, techniques like Lasso regression have emerged as invaluable tools for predictive modeling and feature selection. Lasso, which stands for Least Absolute Shrinkage and Selection Operator, is a regression method that not only predicts outcomes but also sifts through the noise to identify the most influential variables.

This article embarks on a journey through the intricacies of Lasso regression, shedding light on its mathematical foundation, practical applications, and how it differs from other regression methods. Whether you’re a seasoned data scientist or just starting your journey into the world of regression analysis, understanding Lasso’s principles and power can significantly enhance your predictive modeling skills. So, let’s unravel the mysteries of Lasso regression and discover how it can be a game-changer in the realm of data-driven decision-making.

What is the Lasso Regression?

Lasso regression, short for “Least Absolute Shrinkage and Selection Operator,” is a popular regression technique used in data analysis and machine learning. It’s a variation of linear regression that introduces regularization to improve model performance and feature selection. The primary goal of lasso regression is to find the best-fitting linear model while simultaneously shrinking the coefficients of less important features toward zero.

In lasso regression, the regularization term added to the linear regression cost function is the absolute value of the coefficients, multiplied by a tuning parameter (λ). This term penalizes large coefficients, forcing some of them to become exactly zero. As a result, lasso regression effectively performs feature selection by excluding certain features from the model, making it particularly useful when dealing with datasets containing many potentially irrelevant or redundant features.

Lasso regression strikes a balance between fitting the data well and preventing overfitting. By shrinking coefficients toward zero, it encourages a simpler model that generalizes better to new, unseen data. This property makes lasso regression a valuable tool in situations where interpretability and model complexity are crucial considerations.

Through its unique approach to regularization and feature selection, lasso regression offers an effective way to build predictive models while handling multicollinearity and reducing the impact of irrelevant features. In the following sections, we’ll delve deeper into the mechanics, benefits, and applications of lasso regression in various real-world scenarios.

What is the equation of the Lasso Regression?

Lasso regression modifies the standard linear regression equation by adding a regularization term that encourages the model to have small coefficient values. The cost function for lasso regression can be expressed as:

\(\) \[ \text{Cost}(\beta) = \text{Least Squares Loss} + \lambda \sum_{i=1}^{n} |\beta_i| \]

Here’s a breakdown of the components:

• Cost(β): The overall cost or error associated with the model’s predictions based on the coefficients β.
• Least Squares Loss: This is the traditional least squares loss function, which measures the squared difference between the predicted values and the actual target values.
• λ (Lambda): This is the regularization parameter or penalty term. It controls the strength of the regularization. A higher λ results in stronger regularization, which in turn leads to smaller coefficient values. The choice of λ is crucial in controlling the trade-off between model complexity and accuracy.
• Sum Term: This term represents the sum of the absolute values of the coefficient estimates 𝛽i. It’s the L1 norm of the coefficient vector.

The primary objective of lasso regression is to minimize this cost function by adjusting the coefficients 𝛽i while considering the regularization term. The key feature of lasso is that it includes an absolute value in the regularization term, making it capable of shrinking coefficients all the way to zero.

Example:

Let’s illustrate lasso regression with a simple example. Suppose we want to predict house prices based on several features like square footage, number of bedrooms, and location. The lasso regression equation for this problem would be:

\(\) \[ \text{House Price} = \beta_0 + \beta_1 \times \text{Square Footage} + \beta_2 \times \text{Number of Bedrooms} + \beta_3 \times \text{Location} + \ldots \]

In this equation, 𝛽0, 𝛽1, etc., are the coefficients that the lasso algorithm will estimate. The regularization term, controlled by λ, ensures that some of these coefficients may become exactly zero, effectively removing certain features from the model. This feature selection capability is a distinctive advantage of lasso regression, particularly when dealing with datasets with many features or potential multicollinearity issues.

What are the advantages and disadvantages of the Lasso Regression?

Lasso regression is a popular technique in the realm of linear regression that comes with its own set of advantages and disadvantages. In this section, we’ll delve into the specifics of what makes Lasso a valuable tool and where it might have limitations. Understanding these aspects is essential for making informed decisions when applying Lasso regression to real-world data analysis tasks.

Advantages of Lasso Regression:

1. Feature Selection: Lasso regression is renowned for its feature selection capability. It encourages sparsity in the model, which means it tends to force the coefficients of irrelevant or redundant features to exactly zero. This leads to a simpler and more interpretable model. For example, in a housing price prediction model, Lasso might automatically identify that the number of bedrooms and bathrooms are the most crucial predictors while disregarding less relevant features.
2. Prevents Overfitting: Lasso’s regularization term, represented by the (\lambda) (lambda) parameter, helps prevent overfitting. Overfitting occurs when a model fits the training data extremely closely but performs poorly on unseen data. Lasso’s regularization penalizes large coefficient values, effectively reducing the model’s complexity and its tendency to fit noise in the training data.
3. Handles Multicollinearity: Multicollinearity arises when predictor variables in a regression model are highly correlated. This can pose challenges in traditional regression, but Lasso can effectively deal with it. It does so by selecting one of the correlated variables while driving the coefficients of the others to zero. For example, if two variables, such as “income” and “years of education,” are highly correlated, Lasso might choose one and set the other’s coefficient to zero.
4. Robustness to Outliers: Lasso regression is relatively robust to the presence of outliers in the dataset. Outliers are extreme data points that can disproportionately influence a traditional regression model, leading to biased parameter estimates. Lasso’s regularization tends to reduce the impact of outliers, making the model more robust.
5. Interpretability: The simplicity achieved through feature selection in Lasso makes the model more interpretable. In cases where you need to explain the model’s predictions to non-technical stakeholders, a sparse model with fewer predictors is easier to communicate and understand.

Disadvantages of Lasso Regression:

1. Selection Bias: While feature selection is an advantage, it can also lead to selection bias. If the Lasso incorrectly excludes important variables from the model, it may result in a biased model that fails to capture essential relationships in the data.
2. Unstable for Correlated Predictors: Lasso can be unstable when dealing with highly correlated predictors. Small changes in the dataset or the inclusion of slightly different variables can lead to different variable selections. This instability can make it challenging to rely on a specific set of selected variables.
3. Choice of Lambda: Lasso’s effectiveness relies on selecting an appropriate value for the regularization parameter (\lambda) (lambda). Choosing the right (\lambda) requires techniques like cross-validation, which can be computationally intensive and may not always yield an obvious choice.
4. Not Ideal for All Datasets: Lasso is most effective when there’s a genuine reason to believe that some predictors should have exactly zero coefficients. In datasets where all features are likely to be relevant, other regression techniques, such as Ridge regression, which shrinks coefficients towards zero but doesn’t force them to zero, might be more appropriate.
5. Loss of Information: By reducing the magnitude of coefficients, Lasso may lose some information that could be useful in making predictions. In cases where all predictors are genuinely informative, Lasso’s tendency to set some coefficients to zero can result in a less accurate model compared to non-regularized regression methods.

In conclusion, Lasso regression is a powerful tool in the realm of regression analysis, especially when feature selection, dealing with multicollinearity, or preventing overfitting is crucial. However, it’s essential to be aware of its limitations and consider the nature of the dataset and the specific goals of the analysis when deciding whether Lasso or another regression method is most appropriate.

Lasso vs. Ridge vs. Elastic Net

In the realm of linear regression, several regularization techniques aim to improve model performance and address the challenges of multicollinearity. Lasso, Ridge, and Elastic Net are three such techniques, each with its unique characteristics and use cases. Let’s explore how these methods differ and when you might prefer one over the others.

Lasso Regression:

• Advantages:
• Feature Selection: Lasso performs automatic feature selection by driving the coefficients of irrelevant or less important features to zero.
• Simplicity: It’s straightforward to implement and interpret.
• Disadvantages:
• Unstable with Many Features: Lasso can be unstable when dealing with a high number of features, and it might select a subset of them randomly.
• Non-Unique Solutions: For highly correlated features, Lasso may produce non-unique solutions.

Ridge Regression:

• Advantages:
• Stability: Ridge regression is more stable than Lasso when handling multicollinearity.
• Unique Solution: It always produces a unique solution, even with highly correlated features.
• Disadvantages:
• Doesn’t Perform Feature Selection: Ridge doesn’t perform feature selection; it shrinks coefficients toward zero but doesn’t eliminate them.

Elastic Net Regression:

• Advantages:
• Balance: Elastic Net combines the strengths of both Lasso and Ridge. It can perform feature selection and handle multicollinearity effectively.
• Tunability: The combination of L1 (Lasso) and L2 (Ridge) regularization allows you to fine-tune the balance between feature selection and coefficient shrinkage.
• Disadvantages:
• Complexity: Elastic Net involves an additional hyperparameter to control the balance between L1 and L2 regularization, making it slightly more complex than Lasso or Ridge alone.

When to Choose Which:

• Lasso: Use Lasso when you suspect that only a subset of your features is relevant, and you want automatic feature selection. It’s also suitable when dealing with high-dimensional data.
• Ridge: Opt for Ridge when you have multicollinearity issues, and you want a more stable solution. Ridge is also a good choice when you believe that all features contribute to the prediction, but you want to reduce their impact.
• Elastic Net: Elastic Net strikes a balance between Lasso and Ridge and is useful when you need feature selection and multicollinearity handling simultaneously. It provides a more tunable approach.

In practice, the choice among Lasso, Ridge, or Elastic Net depends on your specific data, the problem you’re solving, and the trade-offs you’re willing to make between feature selection and multicollinearity handling. Experimentation and cross-validation are valuable tools for determining which method works best for your particular modeling task.

How can you do Training and Hyperparameter Tuning for Lasso Regression?

Hyperparameter tuning is a vital step in building accurate and robust machine learning models, including Lasso regression. In Lasso regression, the primary hyperparameter to tune is the regularization strength, often denoted as ‘alpha’ (α). This parameter controls the extent to which Lasso penalizes the absolute values of the coefficients.

Here’s a step-by-step guide on how to perform hyperparameter tuning in Lasso regression:

1. Define a Range of Alpha Values:

Start by defining a range of alpha values that you want to explore during the tuning process. This range should span from very small values (close to zero) to larger values, often distributed on a logarithmic scale.

2. Split Your Data:

Divide your dataset into two subsets: a training set and a validation set. The training set is used to train multiple Lasso regression models with different alpha values, while the validation set is employed to evaluate their performance.

3. Train Lasso Models:

Iterate through the predefined alpha values and train a separate Lasso regression model for each alpha using the training dataset. The goal is to assess how different alpha values affect the model’s performance.

4. Evaluate Model Performance:

After training each Lasso model, evaluate its performance on the validation set using an appropriate evaluation metric. Common metrics include R-squared, Mean Squared Error (MSE), or any other suitable metric for your specific problem.

5. Choose the Best Alpha:

Select the alpha value that results in the best model performance on the validation set. This alpha is the one you should use for your final Lasso regression model.

6. Test on Holdout Data:

Once you’ve chosen the best alpha, it’s a good practice to test your selected model on a separate holdout test dataset that it has not encountered during training or validation. This provides a final evaluation of your model’s performance.

7. Cross-Validation (Optional):

For a more robust evaluation, consider using k-fold cross-validation instead of a single train-validation split. Cross-validation helps ensure that your model’s performance is stable across different data splits.

8. Fine-Tuning (Optional):

If necessary, you can further fine-tune other hyperparameters, such as the choice of a specific solver or tolerance level, depending on your software library and specific requirements.

Hyperparameter tuning is an iterative process where you aim to strike the right balance between model complexity (controlled by alpha) and predictive accuracy. Experiment with different alpha values to assess their impact on your model’s performance and choose the one that best aligns with your specific problem and dataset.

How can you implement the Lasso Regression in Python?

Lasso regression, a popular linear regression technique with L1 regularization, can be effectively implemented in Python using libraries like scikit-learn. Below, we’ll walk through the steps to implement Lasso regression with an example using the California Housing dataset, a publicly available dataset commonly used for regression tasks.

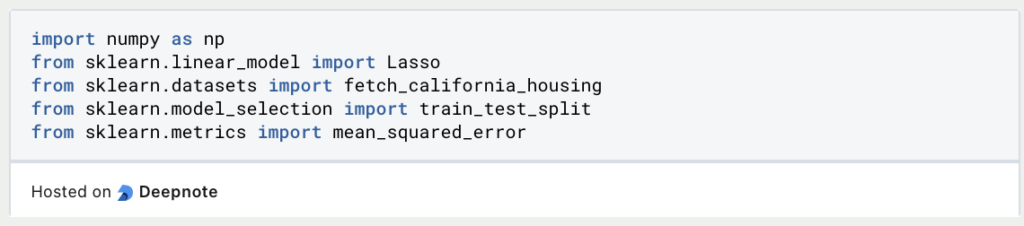
1. Import Necessary Libraries:

Begin by importing the required libraries for your Python environment. You’ll need scikit-learn for modeling, NumPy for numerical operations, and potentially other libraries for data manipulation and visualization.

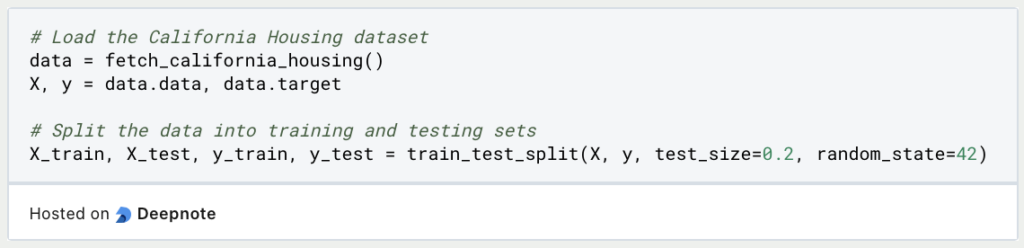
2. Load and Prepare the Dataset:

Load the California Housing dataset, which is available through scikit-learn’s datasets module. Split the data into features (X) and the target variable (y), and further divide it into training and testing sets.

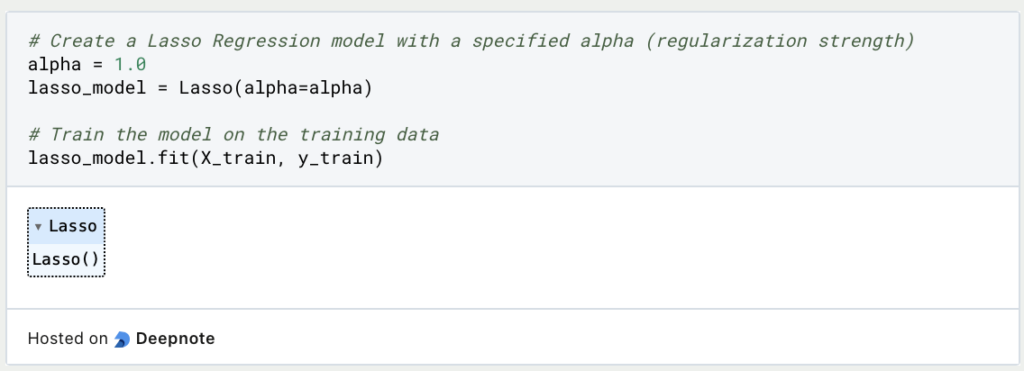
3. Create and Train the Lasso Regression Model:

Next, create an instance of the Lasso regression model, specifying the regularization strength (alpha). Train the model using the training data.

4. Make Predictions:

Use the trained Lasso regression model to make predictions on the test data.

5. Evaluate the Model:

Assess the performance of the Lasso regression model using appropriate evaluation metrics. For regression tasks, metrics like Mean Squared Error (MSE) or R-squared are commonly used.

6. Hyperparameter Tuning (Optional):

You can fine-tune the alpha hyperparameter by experimenting with different values and selecting the one that results in the best model performance. Techniques like cross-validation can help in this process.

This example demonstrates how to implement Lasso regression in Python using the scikit-learn library with the California Housing dataset. Keep in mind that the choice of dataset and specific hyperparameters may vary depending on your particular regression problem.

How do you interpret the parameters of the Lasso Regression?

Interpreting the parameters (coefficients) in a Lasso regression model is essential for understanding the relationship between the independent variables (features) and the dependent variable (target). In Lasso regression, the coefficients are subject to L1 regularization, which can lead to some coefficients being exactly zero. This feature selection property makes interpretation relatively straightforward.

1. Non-Zero Coefficients:

In Lasso regression, some coefficients are usually set to exactly zero as part of the feature selection process. These are the variables that the model considers irrelevant in predicting the target variable. If a coefficient is not zero, it means that the corresponding feature has a non-zero effect on the target.

2. Coefficient Sign:

The sign (positive or negative) of a non-zero coefficient indicates the direction of the relationship between the feature and the target. For example, if the coefficient of a feature is positive, an increase in that feature’s value will lead to an increase in the predicted target variable, and vice versa for a negative coefficient.

3. Magnitude of Coefficients:

The magnitude of the coefficients reflects the strength of the relationship between each feature and the target. Larger coefficient values indicate a stronger influence on the target, while smaller values suggest a weaker influence. You can compare the magnitudes of coefficients to determine which features have a more significant impact.

4. Feature Importance:

By examining the non-zero coefficients, you can identify which features are the most important for predicting the target. Features with non-zero coefficients contribute to the model’s predictive power. This can be valuable for feature selection and simplifying your model.

5. Coefficient Stability:

In Lasso regression, the stability of coefficients can vary with different alpha values (regularization strength). Smaller alpha values tend to produce more stable and interpretable coefficients. Experimenting with alpha values and observing changes in coefficients can help you understand how sensitive your model is to different regularization levels.

6. Domain Knowledge:

While interpreting coefficients is crucial, it’s essential to combine statistical insights with domain knowledge. Understanding the context of your data and how variables relate to each other can provide valuable insights into the practical implications of coefficient values.

Remember that interpreting coefficients in Lasso regression is more straightforward compared to some other regression techniques because of the feature selection property. It allows you to focus on the most relevant variables for your analysis and decision-making.

This is what you should take with you

• Lasso regression is a valuable tool for feature selection, helping identify the most important variables in a dataset.
• It provides robustness to overfitting by adding a penalty term to the linear regression, which can lead to better generalization.
• Lasso’s L1 regularization often leads to sparse solutions, where many coefficients are exactly zero, simplifying the model.
• Lasso and Ridge regression offer different types of regularization, and the choice between them depends on the specific problem and the desired model characteristics.
• Fine-tuning the alpha parameter is crucial for optimizing Lasso regression’s performance.
• Implementing Lasso regression in Python, especially with libraries like scikit-learn, is straightforward, allowing practitioners to apply it to real-world datasets.
• Lasso’s feature selection properties enhance model interpretability, making it a preferred choice in some domains.
• Proper data scaling is essential when using Lasso regression to ensure fair regularization across features.

Other Articles on the Topic of Lasso Regression

You can find the documentation for the Lasso Regression in Scikit-Learn here.