What is Recursion?

Recursion is a fundamental technique in computer science that describes the method by which a programmed function can call itself, thereby gradually breaking down the problem into smaller sub-problems that are easier to solve. This is used, for example, in sorting algorithms or when traversing tree structures.

In this article, we take a closer look at the structure of recursions and understand this method with the help of simple examples in the Python programming language. We also show the advantages and disadvantages of this technique and highlight the differences to normal iterations. To understand the article, you should have a basic knowledge of the Python programming language to be able to follow the examples.

Recursion is a concept from computer science that is characterized by the fact that a function calls itself. The idea behind it is that the function splits the higher-level problem into simpler sub-problems and thus gradually arrives at the solution. This sequence is repeated until the so-called base case is reached and the recursion is stopped.

A Real Example of Recursion | Source: Author

A classic example of recursion is the calculation of the factorial \(n!\) of a number \(n\). This is defined in such a way that the factorial of a number \(n\) is simply the product of the number itself with the factorial of the next smaller integer \(n-1\). In mathematical terms, the factorial follows the following formula:

\(\) \[ n!=n\times\left(n-1\right)!\]

With this formula, the recursive approach of the factorial is already clear, in that for a large number this can simply be calculated until the base case \(1!\) is reached.

In general, there are two types of recursion:

Direct Recursion describes the case where a function calls itself directly. This is by far the most common case in computer science. In the following example, the function f() calls itself within the function sequence until a termination condition is reached.

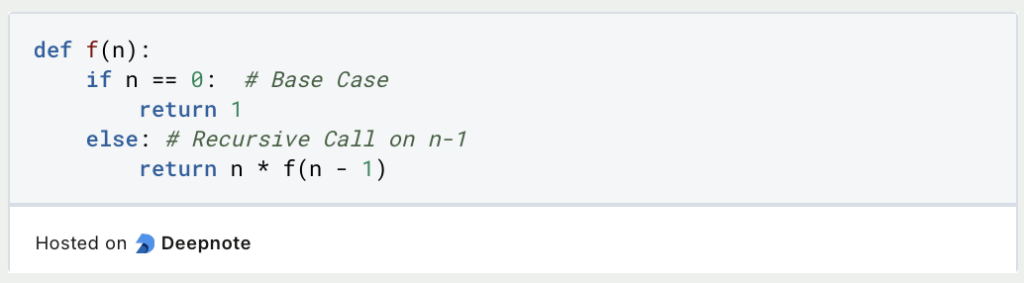
With Indirect Recursion, f() is not called directly via the function itself, but via a second function, such as g(). This creates a chain in which the function f() first calls g(), whereupon g() then calls f() in turn. Indirect recursion is significantly more complex, as more functions are involved in the process, but it still follows the principle of step-by-step problem-solving.

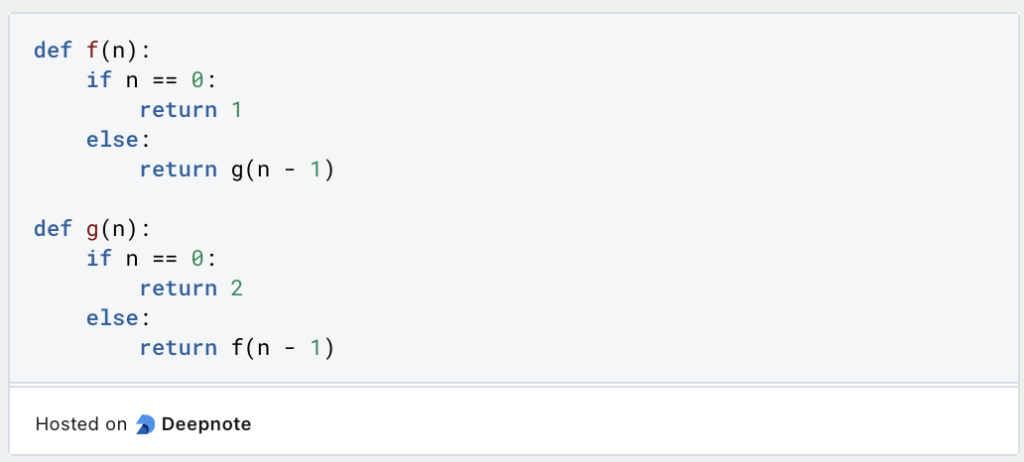
Recursion is a powerful technique in computer science for breaking down complex problems into simpler and solvable sub-problems.

What is the Structure of Recursion Functions?

Recursion consists of two basic components, the base case and the recursive case. These ensure that the function splits the problem into sub-problems until a final solution is found.

Base Case (Termination Condition)

The base case, also known as the termination condition, is the condition that leads to the algorithm being terminated and a solution being output. Without the termination condition, the loop would run endlessly and run into an error as soon as the memory for function calls overflows. The base case is the simplest case of the problem, in which no further recursive calls are necessary.

When calculating the factorial, for example, the base case is reached when n == 0 and no further recursion is necessary:

Recursive Case

The recursive case is the part of the function in which it continues to call itself and breaks the problem down into smaller sub-problems. It must be ensured that the recursive case ensures that the function gradually approaches the base case and does not move away from it. This is shown by the fact that the remaining problem becomes smaller in each step.

In the factorial calculation, the number in the recursive case decreases by 1 in each step until it finally reaches 0:

Recursion is ultimately made up of this interaction between the recursive case and the base case, which ensures that the overall problem is gradually reduced and then finally solved.

What are classic Examples of recursive Functions?

To understand the functionality of recursion in more detail, we will take a closer look at two classic examples with concrete values in this section. These illustrate how smaller subproblems are formed and solved step by step.

Calculating the Factorial

The factorial calculation is mathematically defined as the product of all positive integers up to the number itself, i.e:

\(\) \[ n!=n\times\left(n-1\right)\times\left(n-2\right)\times\ldots\times1 \]

We have already introduced the recursive function for this in Python. It consists of the base case and the recursive case.

Now let’s take a closer look at the individual steps to calculate the factorial of 4. The individual steps are as follows:

With factorial(4), the function first calls the function for factorial(3).
factorial(3) in turn calls factorial(2) and then factorial(1).
This continues until the base case factorial(0) is reached, which in turn returns 0. Here are the individual results of the sub-problems, which are now multiplied:
- factorial(1) returns 1.
- factorial(2) returns 2 * 1 = 2.
- factorial(3) returns 3 * 2 = 6.
- Finally, factorial(4) returns 4 * 6 = 24, which is the final result.

Fibonacci Sequence

The Fibonacci sequence is another mathematical problem that is often solved using recursion. This is a sequence in which any element is calculated from the sum of the two previous elements:

\(\) \[ F(n)\ =\ F(n-1)\ +\ F(n-2) \]

This sequence begins with the values for 0 and 1, which in turn apply:

\(\) \[ F(0)\ =\ 0;\ F(1)\ =\ 1\]

In Python, this recursive sequence can be calculated using the following function:

The function is characterized by the fact that two base cases are defined, namely once for n==0 and once for n==1.

The following sequence then results for fibonacci(5):

At the start, fibonacci(4) and fibonacci(3) are calculated.
These calls are repeated until the base cases are reached.
Finally, the individual results are added together, and the final result fibonacci(5) = 4 + 3 + 2 + 1 + 0 = 10 is output.

Application Examples in Practice

In addition to these mathematical problems, there are also some other practical application examples in which recursion is used:

Sorting algorithms: When sorting elements, such as Python lists, sorting algorithms such as Merge Sort or Quick Sort are used. These divide the lists into smaller elements and sort them independently of each other. These are then merged again.
Search Algorithms: When searching for individual elements in a large data structure, the search is divided into recursive cases by gradually halving the data structure and then searching through the smaller parts.
Tree Traversal: In various file systems, such as XML parsing, recursion is used to traverse the hierarchical structures and thus traverse all points of the tree.
Fractals: Recursion is also used in the creation of so-called fractals. These are geometric patterns that are repeated at different levels of magnification.

Recursion is a versatile concept that is used in a wide range of problems.

What is the Difference between Recursion and Iteration?

In programming, recursion and iteration are two basic approaches to performing repeated calculations. Although both methods lead to the same result, they are fundamentally different in their approach, which means that the choice has a major impact on the efficiency of the algorithm.

A recursive function calls itself to break down the problem into sub-problems and solve them step by step. Iteration, on the other hand, uses loops, such as for or while in Python, to execute certain blocks of code repeatedly.

In the following sections, we will compare these two approaches based on different parameters:

Elegance and Readability: In many cases, recursion offers a much simpler and more readable code, as they adapt to the natural structure of the problem. For simpler problems, however, iteration may appear clearer, for example when traversing data structures such as NumPy arrays or Pandas DataFrames.
Memory: In recursion, each function call generates a certain overhead and is stored in the so-called call stack. In complex cases, this can lead to a so-called stack overflow error, which forces the program to abort. Iteration, on the other hand, is often more efficient as it can access the data structures directly and no additional overhead is generated.
Performance: Due to the memory problem, recursion can be more inefficient than iteration, as saving and restoring contexts takes time and ties up memory.

Recursion is particularly suitable if the problem itself can be formulated recursively and offers a simple and natural solution. Iteration, on the other hand, should be used if the number of iterations is already foreseeable and the state can be easily managed.

What are the Advantages and Disadvantages of Recursion?

Up to this point in the article, recursion has proven to be a very elegant solution for solving complex problems in a simple and efficient way. They are also easier to implement and expect, as they are not as verbose as an iterative solution. Without recursion, complex loops would have to be created for such solutions, which may require additional data structures.

Furthermore, recursion can be used in a wide variety of areas, such as mathematical problems or computer science. The previous section has already presented some problems that can be solved using recursion. In addition, there are many applications that are already recursive from the ground up, such as tree structures.

However, recursion also brings with it some challenges that should be taken into account when implementing it:

Stack Overflow: A stack overflow error occurs when a loop does not end and continues to run until the device’s memory overflows. This can happen with recursions if the base case is not properly defined and therefore never occurs. It must therefore be ensured that the base case can also be reached.
Performance: Compared to iterative approaches, recursion can lead to performance problems, as each function call is stored in the so-called call stack and leads to increased memory consumption, especially with deep recursions. In addition, the function calls are associated with an overhead, whereas iterative approaches can access the data structures directly.
Tail recursion: A special form of recursion is tail recursion, where the last command of a function is a recursive call. In such a case, the compiler or interpreter can optimize the memory requirement by not filling the call stack any further. This saves memory and optimizes performance. However, not all programming languages support such a procedure.

Overall, recursion is a powerful tool for solving complex programming problems. However, before using it, you need to assess whether iterative or recursive use is more suitable.

This is what you should take with you

Recursion is a concept from computer science in which a function calls itself repeatedly.
A distinction is made between two basic components. The basic case describes the condition that causes the algorithm to end. The recursive case, on the other hand, leads to the function being called again.
Recursion is used in a wide variety of mathematical problems and in programming, for example when sorting elements or in search algorithms.
Compared to iteration, i.e. the use of loops, recursion has a greater overhead and can therefore have performance problems. There is also a risk of stack overflow, which can lead to the program being aborted.