Was ist das ARIMA Modell?

ARIMA-Modelle (AutoRegressive Integrated Moving Average) sind eine Klasse von statistischen Modellen, die für Zeitreihenprognosen und -analysen verwendet werden. Sie sind in vielen Bereichen weit verbreitet, darunter Finanzen, Wirtschaft, Technik und Naturwissenschaften. ARIMA-Modelle sind besonders nützlich für die Modellierung von Daten, die eine zeitliche Autokorrelation aufweisen, d. h. die Tendenz einer Zeitreihe, mit ihren vergangenen Werten korreliert zu sein.

In diesem Artikel werden die Prinzipien von ARIMA-Modellen, ihre Anwendungen und ihr potenzieller Nutzen für Industrie und Forschung untersucht. Wir werden erörtern, wie man die geeigneten Modellparameter ermittelt, wie man ein ARIMA-Modell an eine Zeitreihe anpasst und wie man diese Modelle für Prognosen verwendet. Wir werden auch einige der Einschränkungen und Herausforderungen der ARIMA-Modellierung untersuchen und einige fortgeschrittene Techniken für die Zeitreihenanalyse erörtern.

Was sind Zeitreihendaten?

Bei Zeitreihendaten handelt es sich um eine Art von Daten, bei denen Beobachtungen über einen längeren Zeitraum in gleichmäßigen Abständen aufgezeichnet werden. Sie werden häufig in verschiedenen Bereichen verwendet, z. B. in der Finanz-, Wirtschafts-, Ingenieur- und Umweltwissenschaft. Zeitreihendaten unterscheiden sich von anderen Datentypen, da sie eine zeitliche Dimension enthalten, die die Analyse zusätzlich komplex macht. Diese Komplexität ergibt sich aus der Tatsache, dass Zeitreihendaten häufig durch Trends, Saisonalität und andere Formen der zeitlichen Abhängigkeit gekennzeichnet sind, was die Modellierung und Vorhersage zukünftiger Werte erschweren kann.

Bei Zeitreihendaten handelt es sich um eine Abfolge von Beobachtungen, die in regelmäßigen Abständen im Laufe der Zeit gemacht werden. Sie werden häufig in verschiedenen Bereichen wie Wirtschaft, Finanzen, Technik und Umweltwissenschaften verwendet. Zeitreihendaten können aufgrund ihrer Merkmale in verschiedene Typen eingeteilt werden, darunter:

Trend: Ein Trend ist ein langfristiges Muster in den Daten, das eine gleichmäßige Zunahme oder Abnahme im Laufe der Zeit zeigt.
Saisonalität: Die Saisonalität bezieht sich auf das Muster von Schwankungen in den Daten, die sich in regelmäßigen Abständen wiederholen, z. B. täglich, wöchentlich oder jährlich.
Zyklisch: Zyklische Muster sind Schwankungen in den Daten, die nicht regelmäßig oder saisonal sind und oft mit Geschäftszyklen oder wirtschaftlichen Trends in Verbindung gebracht werden.
Unregelmäßig: Unregelmäßige Muster sind zufällige Schwankungen in den Daten, die nicht vorhersehbar sind und keinem Trend, keiner Saisonalität oder einem Zyklus folgen.
Autokorrelation: Autokorrelation liegt vor, wenn ein Datenpunkt in einer Zeitreihe mit einem vergangenen oder zukünftigen Datenpunkt in derselben Reihe korreliert ist.

Was ist ARIMA?

Die ARIMA-Modellierung (Autoregressive Integrated Moving Average) ist eine statistische Methode zur Analyse und Prognose von Zeitreihendaten. Es handelt sich dabei um eine leistungsstarke Technik, die die vergangenen Werte einer Reihe und ihre Veränderungen im Laufe der Zeit berücksichtigt, um Vorhersagen über ihr zukünftiges Verhalten zu treffen. ARIMA-Modelle sind in verschiedenen Bereichen weit verbreitet, darunter Finanzen, Wirtschaft, Klimamodellierung und Technik.

Die Abkürzung ARIMA steht für Autoregressive Integrated Moving Average, was die drei Hauptkomponenten des Modells beschreibt:

Autoregression (AR): Diese Komponente bezieht sich auf die Abhängigkeit der Reihe von ihren eigenen Vergangenheitswerten. Mit anderen Worten: Die zukünftigen Werte der Reihe werden als lineare Kombination ihrer vergangenen Werte modelliert.
Integriert (I): Diese Komponente bezieht sich auf die Notwendigkeit, jegliche Trends oder Saisonalität in der Reihe zu entfernen, um Stationarität zu erreichen. Stationarität ist eine statistische Eigenschaft einer Zeitreihe, die bedeutet, dass sich ihre statistischen Eigenschaften im Laufe der Zeit nicht ändern.
Gleitender Durchschnitt (MA): Diese Komponente bezieht sich auf die Abhängigkeit der Reihe von vergangenen Vorhersagefehlern. Mit anderen Worten: Die zukünftigen Werte der Reihe werden als lineare Kombination vergangener Fehler modelliert und nicht als vergangene Werte der Reihe.

Das ARIMA-Modell wird durch drei Parameter spezifiziert:

p: Die Ordnung der autoregressiven Komponente (AR).
d: Der Grad der Differenzierung, der erforderlich ist, um die Reihe stationär zu machen (I).
q: Die Ordnung der Komponente des gleitenden Durchschnitts (MA).

Diese drei Parameter werden zusammen mit den Daten der Reihe verwendet, um das ARIMA-Modell an die Daten anzupassen. Sobald das Modell angepasst ist, kann es verwendet werden, um Vorhersagen über zukünftige Werte der Reihe zu machen.

ARIMA-Modelle werden häufig um zusätzliche Komponenten erweitert, wie z. B. das saisonale ARIMA (SARIMA), das zusätzlich zu den Standardkomponenten auch saisonale Komponenten enthält. Eine weitere Erweiterung ist das ARIMAX-Modell, das exogene Variablen enthält, die die Vorhersagekraft des Modells verbessern können.

Insgesamt sind ARIMA-Modelle leistungsstarke Instrumente für die Zeitreihenanalyse und -prognose. Sie können komplexe Muster in Zeitreihendaten erfassen und genaue Prognosen für zukünftige Werte liefern. Sie erfordern jedoch eine sorgfältige Abstimmung der Modellparameter und können bei der Anpassung an große Datensätze rechenintensiv sein.

Wie schätzt man die verschiedenen Parameter?

Das ARIMA-Modell ist ein leistungsfähiges Zeitreihenprognosemodell, das zur Analyse und Vorhersage des Verhaltens eines breiten Spektrums realer Phänomene verwendet werden kann. Der Erfolg eines Modells hängt jedoch stark von der genauen Schätzung seiner Parameter ab. Bei der ARIMA-Modellierung besteht das Ziel darin, die Werte der Modellparameter zu schätzen, die die beste Anpassung an die Daten bieten.

Der Prozess der Parameterschätzung bei der ARIMA-Modellierung umfasst die Auswahl der geeigneten Werte für die drei Hauptparameter des Modells, nämlich die autoregressive Ordnung (p), die integrierte Ordnung (d) und die Ordnung des gleitenden Durchschnitts (q). Die autoregressive Ordnung (p) gibt die Anzahl der verzögerten Werte der abhängigen Variable an, die in das Modell einbezogen werden sollen. Die Ordnung des gleitenden Durchschnitts (q) gibt die Anzahl der verzögerten Werte des Fehlerterms an, die in das Modell aufgenommen werden. Die integrierte Ordnung (d) gibt an, wie oft der Differenzierungsoperator auf die Zeitreihendaten angewendet wird, um sie stationär zu machen.

Es gibt mehrere Methoden zur Schätzung der Parameter eines ARIMA-Modells, darunter die Maximum-Likelihood-Schätzung (MLE), die Hannan-Rissanen-Methode und die Methode der bedingten Quadratsumme (CSS). MLE ist die am häufigsten verwendete Methode zur Schätzung von ARIMA-Parametern, da sie die besten Parameterschätzungen liefert, die die Likelihood-Funktion für die beobachteten Daten maximieren. Die Hannan-Rissanen-Methode ist eine zweistufige Methode, bei der zunächst die autoregressiven und gleitenden Durchschnittsparameter geschätzt werden und anschließend die übrigen Parameter mit der CSS-Methode. Die CSS-Methode schätzt die Parameter durch Minimierung der Summe der quadratischen Fehler zwischen den Vorhersagen des Modells und den tatsächlichen Daten.

Sobald die Parameter des ARIMA-Modells geschätzt sind, kann das Modell verwendet werden, um Vorhersagen für zukünftige Werte der Zeitreihe zu treffen. Es ist jedoch wichtig zu beachten, dass die Genauigkeit der Vorhersagen stark von der Qualität der Parameterschätzungen abhängt. Es wird daher empfohlen, das ARIMA-Modell mit Hilfe geeigneter statistischer Tests zu testen und zu validieren, bevor es für Vorhersagen verwendet wird.

Wie erfolgt die Modellauswahl bei ARIMA?

Die Modellauswahl ist ein wichtiger Aspekt der ARIMA-Modellierung, da die Auswahl des optimalen Modells die Genauigkeit der Vorhersagen erheblich verbessern kann. Es gibt mehrere Ansätze für die Modellauswahl, darunter das Akaike-Informationskriterium (AIC), das Bayes’sche Informationskriterium (BIC) und die Kreuzvalidierung.

AIC und BIC sind Informationskriterien, die die Anpassung des Modells an die Daten mit der Anzahl der Parameter im Modell in Einklang bringen. Beide Kriterien bestrafen Modelle mit mehr Parametern, aber BIC bestraft sie stärker als AIC. Niedrigere Werte von AIC und BIC weisen auf eine bessere Modellanpassung hin.

Die Kreuzvalidierung ist eine weitere Methode zur Auswahl des optimalen ARIMA-Modells. Dabei werden die Daten in einen Trainings- und einen Testsatz aufgeteilt und die Leistung des Modells auf dem Testsatz bewertet. Dieser Prozess wird für verschiedene Kombinationen von ARIMA-Parametern wiederholt, und die Kombination, die in der Testgruppe die beste Leistung erbringt, wird ausgewählt.

Im Allgemeinen ist das beste Modell dasjenige, das den niedrigsten AIC- oder BIC-Wert aufweist und in der Kreuzvalidierung auf der Testmenge gut abschneidet. Es ist jedoch wichtig, sich daran zu erinnern, dass die ARIMA-Modellierung nur ein Werkzeug im Werkzeugkasten eines Datenanalysten ist und in Verbindung mit anderen Methoden verwendet werden sollte, um die bestmöglichen Ergebnisse zu erzielen.

Wie wird das Modell bewertet?

Die Bewertung der Leistung eines ARIMA-Modells ist wichtig, um seine Wirksamkeit bei der Vorhersage künftiger Werte zu bestimmen. Es gibt mehrere Messgrößen, die zur Bewertung eines ARIMA-Modells herangezogen werden können, darunter der mittlere quadratische Fehler (MSE), die Wurzel des mittleren quadratischen Fehlers (RMSE), der mittlere absolute Fehler (MAE) und der mittlere absolute Fehler in Prozent (MAPE).

MSE und RMSE messen die durchschnittliche quadratische oder Quadratwurzel der Differenz zwischen den vorhergesagten Werten und den tatsächlichen Werten. MAE misst die durchschnittliche absolute Differenz zwischen den vorhergesagten Werten und den tatsächlichen Werten, und MAPE misst die durchschnittliche prozentuale Differenz zwischen den vorhergesagten Werten und den tatsächlichen Werten.

Zusätzlich zu diesen Metriken können auch grafische Methoden wie Residualdiagramme zur Bewertung eines ARIMA-Modells verwendet werden. Residuen sind die Differenzen zwischen den vorhergesagten und den tatsächlichen Werten, und Residuen-Diagramme können dabei helfen, Muster oder Trends in den Residuen zu erkennen, die darauf hindeuten könnten, dass das Modell nicht alle Informationen in den Daten abbildet.

Es ist wichtig zu beachten, dass ein gutes ARIMA-Modell zwar die Genauigkeit der Vorhersagen verbessern kann, aber nicht die einzige Methode für Prognosen sein sollte. Andere Methoden wie die Regressionsanalyse und Algorithmen des maschinellen Lernens können ebenfalls in Verbindung mit der ARIMA-Modellierung verwendet werden, um die bestmöglichen Ergebnisse zu erzielen.

Wie ist das Modell zu interpretieren?

Zur Interpretation eines ARIMA-Modells gehört es, die Bedeutung und Größe seiner Parameter zu verstehen. Diese Modelle sind durch drei Parameter gekennzeichnet: p, d und q.

Der Parameter p gibt die Anzahl der autoregressiven Terme im Modell an. Autoregressive Terme beziehen sich auf die Abhängigkeit des aktuellen Wertes von früheren Werten. Der Parameter d steht für den Grad der Differenzierung, der auf die Zeitreihendaten angewendet wird, um sie stationär zu machen. Der Parameter q steht für die Anzahl der Terme des gleitenden Durchschnitts im Modell. Die Terme des gleitenden Durchschnitts beziehen sich auf die Abhängigkeit des aktuellen Wertes von den vorherigen Fehlern.

In einem ARIMA-Modell geben die Koeffizienten der autoregressiven und gleitenden Durchschnittsterme die Stärke und Richtung ihrer jeweiligen Beziehung zur abhängigen Variable an. Ein positiver Koeffizient weist auf eine positive Beziehung hin, während ein negativer Koeffizient eine negative Beziehung anzeigt. Die Größe des Koeffizienten zeigt die Stärke der Beziehung an.

Neben der Interpretation der Koeffizienten ist es auch wichtig, die statistische Signifikanz der einzelnen Parameter zu bewerten. Dies kann mithilfe von Hypothesentests erfolgen, wobei die Nullhypothese lautet, dass der Parameter gleich Null ist, und die Alternativhypothese, dass er nicht gleich Null ist. Ist der p-Wert kleiner als das Signifikanzniveau, in der Regel 0,05, so gilt der Parameter als statistisch signifikant und kann in das Modell aufgenommen werden.

Insgesamt geht es bei der Interpretation eines ARIMA-Modells darum, die Beziehung zwischen der abhängigen Variable und ihren historischen Werten sowie die statistische Signifikanz und Größe der Modellparameter zu verstehen. Dieses Verständnis kann genutzt werden, um Vorhersagen über zukünftige Werte der abhängigen Variable zu treffen.

Was sind die Anwendungen von ARIMA-Modellen?

ARIMA-Modelle werden häufig in der Zeitreihenanalyse und -prognose verwendet. Hier sind einige gängige Anwendungen dieser Modelle:

Wirtschaft und Finanzen: ARIMA-Modelle werden zur Modellierung und Vorhersage wirtschaftlicher und finanzieller Zeitreihen wie Aktienkurse, Wechselkurse und Inflationsraten verwendet. Mit diesen Modellen lassen sich Trends, Zyklen und andere Muster in den Daten erkennen, was bei fundierten Investitionsentscheidungen hilfreich sein kann.
Vertrieb und Marketing: ARIMA-Modelle werden zur Prognose des Absatzes und der Nachfrage nach Produkten und Dienstleistungen verwendet. Durch die Analyse vergangener Verkaufsdaten können Unternehmen mithilfe dieser Modelle saisonale Trends und andere Muster erkennen, die ihnen helfen können, bessere Entscheidungen über Bestandsmanagement, Produktionsplanung und Preisgestaltung zu treffen.
Energie und Versorgungsunternehmen: ARIMA-Modelle werden zur Vorhersage des Energiebedarfs, z. B. des Strom- und Gasverbrauchs, verwendet. Diese Modelle können Versorgungsunternehmen dabei helfen, ihre Produktions- und Vertriebsaktivitäten effizienter zu planen, und auch Regierungen bei der Planung des künftigen Energiebedarfs unterstützen.
Gesundheit und Medizin: ARIMA-Modelle werden in der medizinischen Forschung zur Modellierung und Vorhersage von Krankheitsausbrüchen, Krankenhauseinweisungen und anderen gesundheitsbezogenen Zeitreihendaten verwendet. Diese Modelle können Beamten des öffentlichen Gesundheitswesens dabei helfen, den künftigen Bedarf an medizinischer Versorgung zu planen und die Ressourcen effizienter zu verteilen.
Wettervorhersage: ARIMA-Modelle werden bei der Wettervorhersage verwendet, um verschiedene Wettervariablen wie Temperatur, Niederschlag und Windgeschwindigkeit zu modellieren und vorherzusagen. Diese Modelle können Meteorologen dabei helfen, genaue Vorhersagen über das Wetter zu treffen, die zum Schutz von Menschen und Eigentum vor extremen Wetterereignissen genutzt werden können.

Im Allgemeinen sind ARIMA-Modelle immer dann nützlich, wenn es darum geht, Zeitreihendaten zu modellieren und vorherzusagen sowie Trends, Zyklen und andere Muster in den Daten zu erkennen.

Wie implementiert man das ARIMA-Modell in Python?

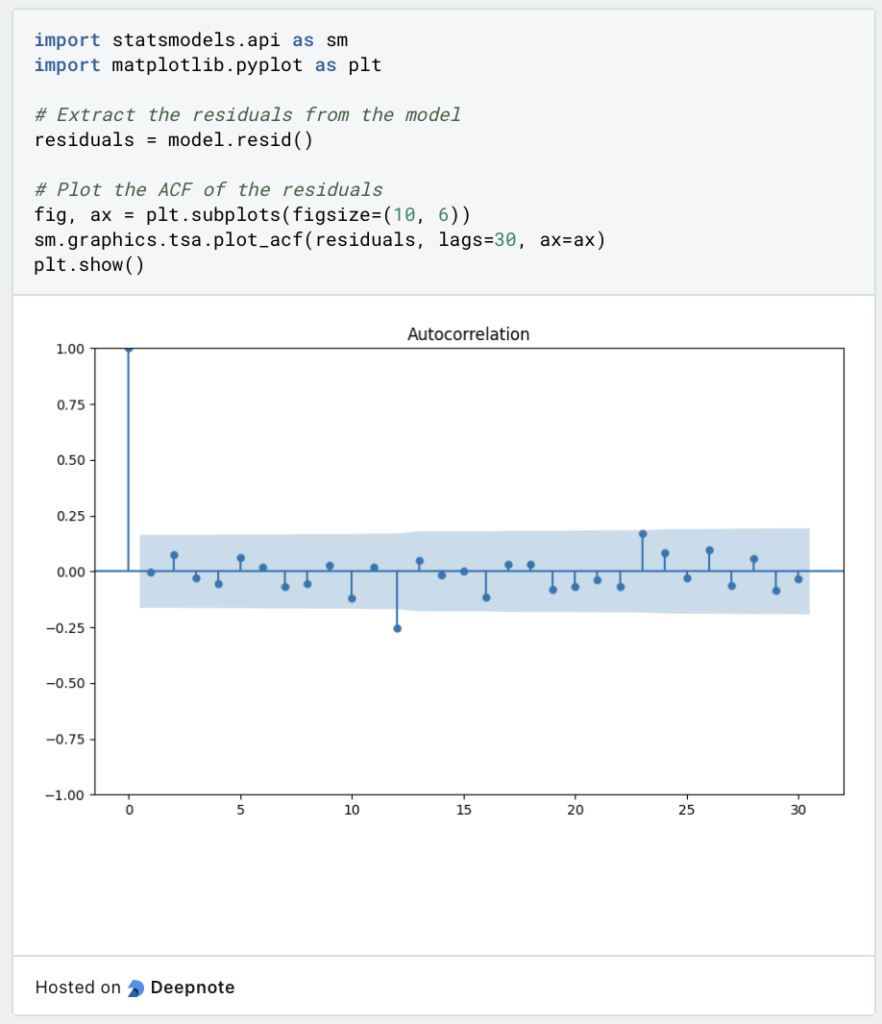
Das ARIMA-Modell (Autoregressive Integrated Moving Average) ist ein leistungsfähiges Werkzeug für die Prognose von Zeitreihen. In Python können wir ARIMA-Modelle mithilfe der statsmodels-Bibliothek implementieren. Lassen Sie uns ein Beispiel anhand eines öffentlich zugänglichen Datensatzes durchgehen.

Für dieses Beispiel verwenden wir den Datensatz “Air Passengers”, der die monatliche Zahl der Passagiere internationaler Fluggesellschaften enthält. Wir können den Datensatz mit der read_csv-Funktion von Pandas laden:

Sehen wir uns die Daten an, indem wir die ersten Zeilen ausgeben:

Als Nächstes werden wir die Spalte “Month” in ein Datumsformat konvertieren, um mit Zeitreihendaten arbeiten zu können:

Zur besseren Handhabung von Zeitreihendaten können wir die Spalte “Month” als Index des DataFrame festlegen:

Um ein ARIMA-Modell anzupassen, müssen wir die Reihenfolge der Differenzierung, der autoregressiven (AR) Terme und der Terme des gleitenden Durchschnitts (MA) bestimmen. Wir können die Funktion auto_arima aus der pmdarima-Bibliothek verwenden, um automatisch die optimalen Parameter auszuwählen:

Sobald wir die optimalen Parameter haben, können wir das ARIMA-Modell an die Daten anpassen:

Um Vorhersagen zu treffen, können wir die predict Methode verwenden. Nehmen wir zum Beispiel eine Prognose für die nächsten 12 Monate:

Schließlich können wir die ursprünglichen Daten und die prognostizierten Werte visualisieren:

Wenn Du diese Schritte befolgst, kannst Du ein ARIMA-Modell in Python unter Verwendung eines öffentlich verfügbaren Datensatzes implementieren. Experimentiere mit verschiedenen Datensätzen und passe die Parameter an, um die Genauigkeit des Modells zu verbessern.

Denke daran, die Leistung des Modells anhand geeigneter Metriken zu bewerten und zusätzliche Techniken wie die Kreuzvalidierung in Betracht zu ziehen, um seine Robustheit zu beurteilen.

Das solltest Du mitnehmen

ARIMA-Modelle sind ein beliebtes und leistungsfähiges Verfahren zur Modellierung von Zeitreihen, das zur Vorhersage künftiger Werte auf der Grundlage vergangener Beobachtungen verwendet wird.
Sie können sowohl mit stationären als auch mit nicht-stationären Daten umgehen, was sie sehr vielseitig macht.
Parameterschätzung, Modellauswahl und Modellbewertung sind allesamt wichtige Schritte bei der Erstellung eines zuverlässigen und genauen ARIMA-Modells.
ARIMA-Modelle werden in der Praxis häufig eingesetzt, z. B. zur Vorhersage von Finanzdaten, Aktienkursen, Wettermustern und vielem mehr.
ARIMA-Modelle haben zwar ihre Stärken, aber auch ihre Grenzen und sollten zusammen mit anderen Techniken verwendet werden, um eine umfassende Analyse von Zeitreihendaten zu ermöglichen.