Zeitreihendaten sind eine Art von Daten, bei denen Beobachtungen im Laufe der Zeit in gleichmäßigen Abständen aufgezeichnet werden. Sie werden häufig in verschiedenen Bereichen verwendet, z. B. in der Finanz-, Wirtschafts-, Ingenieur- und Umweltwissenschaft. Zeitreihendaten unterscheiden sich von anderen Datentypen, da sie eine zeitliche Dimension enthalten, die die Analyse zusätzlich komplex macht. Diese Komplexität ergibt sich aus der Tatsache, dass Zeitreihendaten häufig durch Trends, Saisonalität und andere Formen der zeitlichen Abhängigkeit gekennzeichnet sind, was die Modellierung und Vorhersage zukünftiger Werte erschweren kann.

In diesem Artikel werden die wichtigsten Konzepte und Methoden der Zeitreihenanalyse sowie einige gängige Anwendungen und Herausforderungen im Zusammenhang mit dieser Art von Daten erörtert.

Was sind Zeitreihendaten?

Zeitreihendaten sind eine bestimmte Art von Daten, bei denen Beobachtungen in regelmäßigen Abständen über einen kontinuierlichen Zeitraum aufgezeichnet werden. Im Gegensatz zu Querschnittsdaten, die Informationen zu einem bestimmten Zeitpunkt erfassen, geben Zeitreihendaten Aufschluss darüber, wie sich Variablen im Laufe der Zeit verändern.

Sie weisen einzigartige Merkmale auf, die sie von anderen Datentypen unterscheiden. Zu diesen Merkmalen gehören:

• Zeitliche Ordnung: Zeitreihendaten sind von Natur aus geordnet, wobei die Beobachtungen in chronologischer Reihenfolge angeordnet sind. Dieser zeitliche Aspekt ermöglicht die Analyse von Trends, Mustern und Abhängigkeiten im Zeitverlauf.
• Zeitabhängige Beziehungen: Zeitreihendaten weisen häufig Abhängigkeiten auf, wie z. B. Autokorrelation, bei der der Wert einer Variablen zu einem bestimmten Zeitpunkt mit ihren früheren Werten in Beziehung steht. Das Verständnis dieser Abhängigkeiten ist für eine genaue Modellierung und Vorhersage von entscheidender Bedeutung.
• Saisonalität und Trends: Zeitreihendaten weisen häufig wiederkehrende Muster und Trends auf, die auf verschiedene Faktoren wie Saisonalität (z. B. tägliche, wöchentliche oder jährliche Muster) oder langfristige Trends (z. B. Aufwärts- oder Abwärtsbewegungen im Laufe der Zeit) zurückzuführen sind.
• Unregelmäßige Stichprobenintervalle: Zeitreihendaten werden zwar in der Regel in regelmäßigen Abständen erhoben, können aber auch unregelmäßige Stichprobenintervalle aufweisen. Diese Unregelmäßigkeit stellt eine Herausforderung bei der Datenvorverarbeitung und -analyse dar.
• Zeitabhängige Variation: Zeitreihendaten weisen im Laufe der Zeit oft ein unterschiedliches Maß an Variabilität oder Volatilität auf. Die Identifizierung und Modellierung dieser Schwankungen ist für das Verständnis der den Daten innewohnenden Unsicherheit unerlässlich.

Die Analyse von Zeitreihendaten spielt in verschiedenen Bereichen eine wichtige Rolle, z. B. im Finanzwesen, in der Wirtschaft, in der Klimawissenschaft, bei Umsatzprognosen und in vielen anderen Bereichen. Durch die Untersuchung historischer Muster und Beziehungen ermöglicht uns die Zeitreihenanalyse, fundierte Vorhersagen zu treffen, Anomalien zu erkennen und Einblicke in die zugrunde liegende Dynamik zu gewinnen.

Warum ist die Zeitreihenanalyse wichtig?

Die Zeitreihenanalyse ist ein leistungsfähiges Instrument zum Verständnis und zur Gewinnung von Erkenntnissen aus Daten, die sich im Laufe der Zeit entwickeln. Sie ist aus den folgenden Gründen in verschiedenen Bereichen und Branchen von großer Bedeutung:

1. Erkennung von Trends: Die Zeitreihenanalyse hilft bei der Erkennung von Trends und Mustern in den Daten. Durch die Untersuchung historischer Datenpunkte ist es möglich, Aufwärts- oder Abwärtstrends zu erkennen, so dass Unternehmen fundierte Entscheidungen und Vorhersagen über zukünftige Ergebnisse treffen können.
2. Prognosen und Vorhersagen: Die Zeitreihenanalyse ermöglicht genaue Prognosen und Vorhersagen für künftige Werte auf der Grundlage historischer Datenmuster. Dies ist besonders wertvoll in Bereichen wie Absatzprognosen, Nachfragevorhersagen, Börsenanalysen und Ressourcenplanung, wo genaue Vorhersagen für eine effektive Entscheidungsfindung entscheidend sind.
3. Erkennung von Anomalien: Die Zeitreihenanalyse hilft bei der Erkennung von Anomalien oder Ausreißern in Daten. Diese Anomalien können auf kritische Ereignisse oder ungewöhnliche Verhaltensweisen hinweisen, die Aufmerksamkeit erfordern. Durch die frühzeitige Erkennung solcher Anomalien können Unternehmen rechtzeitig Maßnahmen ergreifen, um Risiken zu mindern oder neue Chancen zu nutzen.
4. Analyse der Saisonalität: Viele Zeitreihendaten weisen saisonale Muster auf, wie etwa tägliche, wöchentliche, monatliche oder jährliche Schwankungen. Die Zeitreihenanalyse ermöglicht die Identifizierung und das Verständnis dieser saisonalen Muster, so dass Unternehmen ihre Strategien entsprechend anpassen können. So können Einzelhändler beispielsweise Werbeaktionen auf der Grundlage wöchentlicher oder jährlicher Einkaufstrends planen.
5. Leistungsbewertung: Die Zeitreihenanalyse bietet die Möglichkeit, die Leistung eines Systems oder Prozesses im Laufe der Zeit zu bewerten. Durch die Verfolgung relevanter Metriken und den Vergleich mit historischen Daten können Unternehmen die Wirksamkeit ihrer Strategien bewerten, verbesserungswürdige Bereiche ermitteln und ihre Abläufe optimieren.

Zusammenfassend lässt sich sagen, dass die Zeitreihenanalyse für das Verständnis und die Nutzung von Daten, die sich im Laufe der Zeit entwickeln, von großer Bedeutung ist. Durch die Analyse historischer Muster, die Identifizierung von Trends und die Erstellung präziser Vorhersagen können Unternehmen wertvolle Einblicke gewinnen, fundierte Entscheidungen treffen, ihre Abläufe optimieren und auf dem dynamischen und sich entwickelnden Markt von heute wettbewerbsfähig bleiben.

Wie werden Zeitreihendaten vorverarbeitet?

Die Datenvorverarbeitung spielt bei der Zeitreihenanalyse eine entscheidende Rolle, um genaue und zuverlässige Ergebnisse zu gewährleisten. Sie umfasst verschiedene Techniken zur Bewältigung gängiger Probleme, die bei Zeitreihendaten auftreten, darunter die Behandlung fehlender Werte, Glättung und Resampling.

Eine häufige Herausforderung sind fehlende Werte, die sich negativ auf die Analyse auswirken können. Imputationstechniken wie Forward Fill, Backward Fill oder Interpolation können verwendet werden, um fehlende Werte auszugleichen. Alternativ dazu können Zeitpunkte mit signifikanten fehlenden Werten entfernt werden, wenn eine genaue Imputation nicht möglich ist.

Glättungsverfahren werden eingesetzt, um das Rauschen und die Variabilität in Zeitreihendaten zu reduzieren und die zugrunde liegenden Muster aufzudecken. Gleitende Durchschnitte, wie der einfache gleitende Durchschnitt oder der exponentiell gewichtete gleitende Durchschnitt, werden häufig zur Glättung verwendet. Bei diesen Techniken wird der Durchschnitt eines gleitenden Fensters von Datenpunkten berechnet, um langfristige Trends hervorzuheben und kurzfristige Schwankungen zu minimieren.

Beim Resampling wird die Häufigkeit der Zeitreihendaten geändert. Beim Upsampling wird die Häufigkeit durch Interpolation erhöht, um häufigere oder feinere Beobachtungen zu erfassen, während beim Downsampling die Häufigkeit durch Aggregation mehrerer Beobachtungen zu einem einzigen Datenpunkt verringert wird. Resampling hilft bei der Anpassung der Daten an eine gemeinsame Frequenz oder bei der Verringerung des Rechenaufwands.

Der Umgang mit Ausreißern ist bei der Zeitreihenanalyse von wesentlicher Bedeutung. Ausreißer sind Extremwerte, die erheblich vom erwarteten Muster abweichen. Techniken wie der Z-Score, die mittlere absolute Abweichung (MAD) oder robuste statistische Methoden können eingesetzt werden, um Ausreißer zu identifizieren und angemessen zu behandeln.

Normalisierung und Skalierung sind wichtig, um sicherzustellen, dass Variablen mit unterschiedlichen Skalen einen vergleichbaren Einfluss auf die Analyse haben. Normalisierungstechniken wie Min-Max-Skalierung, z-Score-Normalisierung oder Dezimalskalierung können angewendet werden, um Variablen auf eine einheitliche Skala zu bringen.

Das Feature-Engineering ist ein weiterer wichtiger Schritt in der Datenvorverarbeitung für die Zeitreihenanalyse. Dabei werden neue Variablen erstellt oder bestehende Variablen transformiert, um die Vorhersagekraft des Modells zu verbessern. Techniken wie das Nachziehen von Variablen, die Differenzierung oder die Erstellung rollierender Statistiken können eingesetzt werden, um aussagekräftige Merkmale aus den Zeitreihendaten zu extrahieren.

Durch eine effektive Datenvorverarbeitung, einschließlich der Behandlung fehlender Werte, Glättung, Resampling, Behandlung von Ausreißern, Normalisierung und Feature Engineering, können Zeitreihendaten für die weitere Analyse angemessen vorbereitet werden. Diese Vorverarbeitungstechniken tragen zu genaueren und aussagekräftigeren Erkenntnissen aus der Zeitreihenanalyse bei.

Welche Modelle werden verwendet, um eine Zeitreihe in die Zukunft zu prognostizieren?

Bei der Zeitreihenprognose können je nach den Merkmalen der Daten und der spezifischen Prognoseaufgabe verschiedene Modelle verwendet werden. Hier sind einige häufig verwendete Modelle:

• Autoregressiver integrierter gleitender Durchschnitt (ARIMA): ARIMA ist ein beliebtes Modell für univariate Zeitreihenprognosen. Es kombiniert autoregressive (AR), differenzierende (I) und gleitende Durchschnittskomponenten (MA). ARIMA-Modelle sind in der Lage, sowohl den Trend als auch die Saisonalität in den Daten zu erfassen.

• Saisonales ARIMA (SARIMA): SARIMA ist eine Erweiterung des ARIMA-Modells, die neben dem Trend auch die Saisonalität berücksichtigt. Es ist nützlich, wenn die Daten wiederkehrende Muster über bestimmte Zeitintervalle aufweisen, z. B. täglich, monatlich oder jährlich.
• Exponentielle Glättungsmethoden: Zu den exponentiellen Glättungsmethoden gehören Modelle wie Simple Exponential Smoothing (SES), Holt’s Linear Exponential Smoothing und Holt-Winters’ Seasonal Exponential Smoothing. Diese Modelle eignen sich für die Prognose von Zeitreihen mit oder ohne Trend und Saisonalität. Sie weisen älteren Beobachtungen exponentiell abnehmende Gewichte zu und geben jüngeren Daten mehr Bedeutung.
• Vektorielle Autoregression (VAR): VAR ist ein multivariates Zeitreihenmodell, das die Beziehung zwischen mehreren Variablen erfasst. Es ermöglicht die Analyse und Vorhersage der gegenseitigen Abhängigkeiten zwischen diesen Variablen. VAR-Modelle sind nützlich, wenn die Prognose einer Variablen von den verzögerten Werten anderer Variablen abhängt.
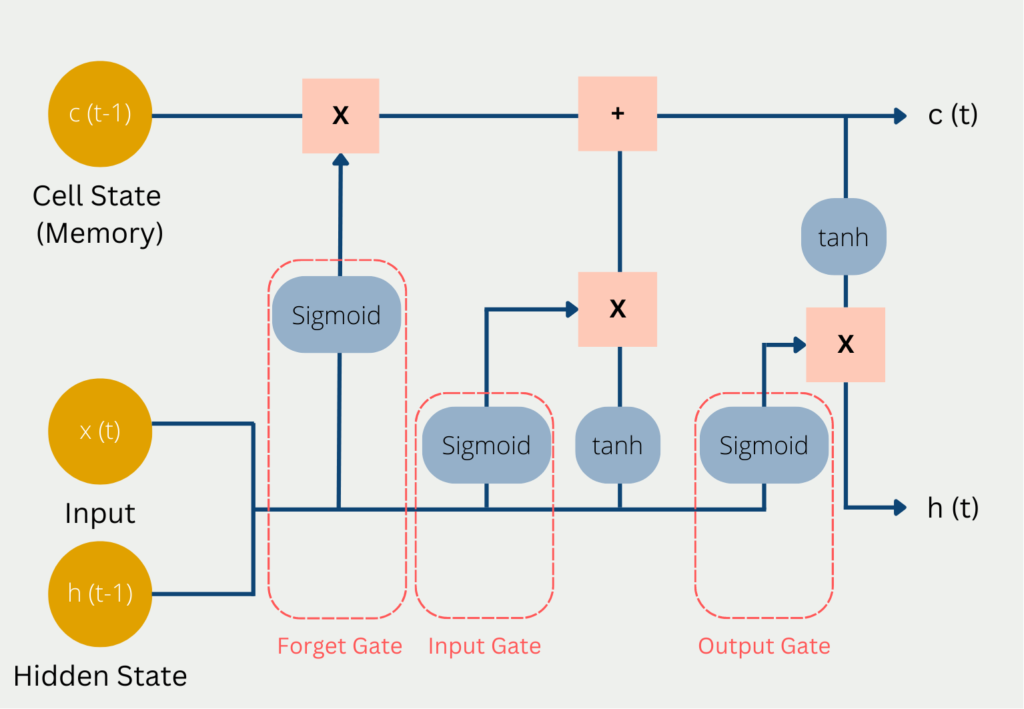
• Netzwerke mit langem Kurzzeitgedächtnis (LSTM): LSTM ist eine Art rekurrentes neuronales Netz (RNN), das effektiv langfristige Abhängigkeiten und Muster in sequentiellen Daten erfassen kann. Es kann für Zeitreihenprognosen verwendet werden, indem es aus historischen Mustern lernt und auf der Grundlage des erlernten Kontexts Vorhersagen trifft.

• Prophet: Prophet ist ein von Facebook entwickeltes Zeitreihenprognosemodell. Es wurde entwickelt, um Zeitreihendaten mit mehreren saisonalen Komponenten zu verarbeiten, einschließlich täglicher, wöchentlicher, monatlicher und jährlicher Muster. Prophet berücksichtigt verschiedene Komponenten wie Trend, Saisonalität und Ferieneffekte, um genaue Prognosen zu erstellen.
• Gaußsche Prozesse (GP): GP-Modelle sind probabilistische Modelle, die nicht-lineare Abhängigkeiten in Zeitreihendaten erfassen können. Sie sind flexibel und können mit Unsicherheitsschätzungen umgehen. GP-Modelle sind geeignet, wenn der zugrunde liegende Datenerzeugungsprozess als glatt und kontinuierlich angesehen wird.
• Zustandsraum-Modelle: Zustandsraummodelle, wie der Kalman-Filter und seine Erweiterungen, werden zur Modellierung dynamischer Systeme mit verborgenen Zuständen verwendet. Diese Modelle können komplexe Beziehungen zwischen beobachteten Variablen und latenten Variablen erfassen, was sie für die Vorhersage von Zeitreihen nützlich macht.

Jedes dieser Modelle hat seine Stärken und Grenzen, und die Wahl des Modells hängt von Faktoren wie der Art der Daten, dem Vorhandensein eines Trends oder einer Saisonalität, den verfügbaren Rechenressourcen und dem gewünschten Grad der Interpretierbarkeit ab. Oft ist es von Vorteil, mit mehreren Modellen zu experimentieren und dasjenige auszuwählen, das am besten zu den Daten passt und genaue Prognosen für die jeweilige Prognoseaufgabe liefert.

Wie bewertet man Zeitreihenmodelle?

Die Bewertung von Zeitreihenmodellen ist wichtig, um die Qualität und Genauigkeit der Vorhersagen zu verstehen. Der gängigste Ansatz ist die Verwendung historischer Daten zur Schätzung der Modellparameter und die Prüfung der Vorhersagekraft anhand eines separaten Datensatzes. Die folgenden Bewertungstechniken werden üblicherweise für Zeitreihenmodelle verwendet:

1. Mittlerer quadratischer Fehler (MSE): Damit wird die Differenz zwischen vorhergesagten und tatsächlichen Werten gemessen. Je kleiner der Wert des MSE ist, desto besser ist das Modell.
2. Root Mean Squared Error (RMSE): Dies ist die Quadratwurzel des MSE und gibt ein Maß für den typischen Fehler des Modells in denselben Einheiten wie die Daten an.
3. Mittlerer absoluter Fehler (MAE): Dieser Wert misst die absolute Differenz zwischen den vorhergesagten und den tatsächlichen Werten. Er ist weniger empfindlich gegenüber Ausreißern als der MSE.
4. Mittlerer absoluter prozentualer Fehler (MAPE): Dieser Wert misst die prozentuale Differenz zwischen vorhergesagten und tatsächlichen Werten.
5. Symmetrischer mittlerer absoluter prozentualer Fehler (SMAPE): Ähnlich wie MAPE, jedoch wird hier der Durchschnitt der prozentualen Differenz zwischen vorhergesagten und tatsächlichen Werten gemessen.
6. Theils U-Statistik: Sie misst die relative Genauigkeit der Vorhersage im Vergleich zur naiven Vorhersage, d. h. der Vorhersage für die nächste Periode, die dem Wert der aktuellen Periode entspricht.
7. Akaike Information Criterion (AIC) und Bayesian Information Criterion (BIC): Dies sind Maßstäbe für die Anpassungsgüte eines Modells, die auch die Anzahl der Parameter im Modell berücksichtigen. Niedrigere Werte von AIC und BIC weisen auf bessere Modelle hin.
8. Varianzzerlegung der Vorhersagefehler (FEVD): Sie misst den Beitrag der einzelnen Schocks zur Varianz des Prognosefehlers.
9. Diebold-Mariano-Test: Hierbei handelt es sich um einen statistischen Test, mit dem die Vorhersagegenauigkeit zweier Modelle verglichen werden kann.

Es ist wichtig zu beachten, dass die beste Bewertungsmetrik von dem Problem und den Daten abhängt. Eine gute Praxis ist es, verschiedene Bewertungsmetriken zu vergleichen und diejenige zu wählen, die für die jeweilige Anwendung am besten geeignet ist.

Was sind die Herausforderungen und Überlegungen bei der Arbeit mit Zeitreihendaten?

Die Analyse und Vorhersage von Zeitreihendaten bringt einzigartige Herausforderungen und Überlegungen mit sich. Diese Faktoren spielen eine entscheidende Rolle beim Verständnis und bei der Erstellung von Vorhersagen auf der Grundlage von zeitabhängigen Daten. Hier sind einige wichtige Aspekte, die es zu beachten gilt:

Zeitabhängigkeit: Zeitreihendaten beruhen auf der Beziehung zwischen vergangenen und aktuellen Beobachtungen. Jeder Datenpunkt wird durch seinen zeitlichen Kontext beeinflusst, und diese Abhängigkeit erfordert spezielle Modellierungstechniken.

Saisonalität und Trend: Viele Zeitreihen weisen wiederkehrende Muster auf, wie etwa tägliche, wöchentliche oder jährliche Schwankungen. Die Identifizierung und Berücksichtigung dieser Muster sowie die Erfassung langfristiger Trends sind für genaue Prognosen unerlässlich.

Nicht-Stationarität: Bei Zeitreihendaten kommt es im Laufe der Zeit häufig zu Veränderungen der statistischen Eigenschaften, wie Mittelwert und Varianz. Diese Veränderungen können auf verschiedene Faktoren zurückzuführen sein und erfordern Transformationen, um die Daten für Modellierungszwecke stationär zu machen.

Fehlende Daten: Zeitreihendaten können aus verschiedenen Gründen Lücken oder fehlende Werte aufweisen. Der Umgang mit fehlenden Daten ist entscheidend für die Integrität der Analyse und der Prognosen. Techniken wie Interpolation oder Imputation können verwendet werden, um

Ausreißer und Anomalien: Anomalien und Ausreißer, d. h. Datenpunkte, die erheblich vom erwarteten Muster abweichen, können die Modelle verzerren und die Prognosegenauigkeit beeinträchtigen. Robuste Methoden zur Erkennung von Ausreißern sind unerlässlich, um zuverlässige Ergebnisse zu gewährleisten.

Wechselwirkungen zwischen Variablen: Bei der multivariaten Zeitreihenanalyse ist das Verständnis der Wechselwirkungen zwischen den Variablen entscheidend. Variablen können komplexe Abhängigkeiten und Beziehungen aufweisen, die eine sorgfältige Modellierung erfordern, um diese Interaktionen genau zu erfassen.

Computerkomplexität: Die Analyse und Modellierung von Zeitreihendaten kann rechenintensiv sein, insbesondere bei großen Datensätzen oder komplexen Modellen. Der Einsatz effizienter Algorithmen und ausreichender Rechenressourcen ist notwendig, um die rechnerischen Anforderungen zu bewältigen.

Validierung und Bewertung: Die Validierung und Evaluierung von Zeitreihenmodellen stellt aufgrund der sequentiellen Natur der Daten eine besondere Herausforderung dar. Techniken wie die Walk-Forward-Validierung oder die Rolling-Origin-Validierung können eingesetzt werden, um die Leistung des Modells bei ungesehenen Daten zu bewerten.

Interpretierbarkeit: Komplexe Modelle können zwar genaue Prognosen liefern, ihre Interpretierbarkeit kann jedoch eingeschränkt sein. Es ist wichtig, ein Gleichgewicht zwischen Modellkomplexität und Interpretierbarkeit zu finden und dabei die spezifischen Bedürfnisse und Anforderungen der Analyse zu berücksichtigen.

Durch die Bewältigung dieser Herausforderungen und fundierte Entscheidungen in Bezug auf die Datenvorverarbeitung, Modellierungstechniken und Auswertungsmethoden können Analysten Zeitreihendaten effektiv steuern und aussagekräftige Erkenntnisse und genaue Prognosen gewinnen.

Welche Anwendungen nutzen die Zeitreihenanalyse?

Die Zeitreihenanalyse ist ein leistungsfähiges Instrument, das in zahlreichen Branchen Anwendung findet. Hier sind einige Beispiele:

1. Finanzen: Die Zeitreihenanalyse wird im Finanzwesen häufig zur Vorhersage von Aktienkursen, Wechselkursen und Zinssätzen verwendet.
2. Wirtschaft: Die Zeitreihenanalyse wird in den Wirtschaftswissenschaften zur Analyse makroökonomischer Variablen wie Bruttoinlandsprodukt, Inflation und Arbeitslosenquote verwendet.
3. Marketing: Die Zeitreihenanalyse kann zur Analyse von Verkaufsdaten, zur Ermittlung von Trends und zur Vorhersage künftiger Verkäufe verwendet werden.
4. Gesundheitswesen: Mit Hilfe der Zeitreihenanalyse können medizinische Daten, wie z. B. die Vitalwerte von Patienten, analysiert und Trends und Muster ermittelt werden, die bei der Diagnose und Behandlung hilfreich sein können.
5. Umweltwissenschaften: Die Zeitreihenanalyse kann zur Analyse von Daten über den Klimawandel, einschließlich Temperatur- und Niederschlagsmustern, verwendet werden.
6. Verkehrswesen: Zeitreihenanalysen können zur Vorhersage von Verkehrsmustern und zur Optimierung von Transportrouten verwendet werden.
7. Fertigung: Mit Hilfe der Zeitreihenanalyse lassen sich Trends und Muster in Produktionsdaten erkennen und die Nachfrage nach Produkten vorhersagen.
8. Sozialwissenschaften: Die Zeitreihenanalyse kann zur Analyse von Daten über Kriminalitätsraten, Bevölkerungsdemografie und andere soziale Phänomene verwendet werden.

Insgesamt ist die Zeitreihenanalyse ein wertvolles Instrument, um komplexe Systeme zu verstehen und fundierte Entscheidungen auf der Grundlage historischer Muster und Trends zu treffen.

Das solltest Du mitnehmen

• Zeitreihendaten sind eine Art von Daten, die chronologisch geordnet sind.
• Sie können mit verschiedenen Zeitreihenmodellen analysiert werden, z. B. ARIMA, SARIMA und exponentielle Glättung.
• Die Vorverarbeitung von Zeitreihendaten umfasst die Behandlung fehlender Werte und Ausreißer sowie die Skalierung der Daten.
• Die Bewertung von Zeitreihenmodellen kann mit verschiedenen Techniken erfolgen, z. B. mit dem mittleren quadratischen Fehler, dem mittleren quadratischen Fehler und dem mittleren absoluten Fehler in Prozent.
• Die Zeitreihenanalyse findet in verschiedenen Bereichen Anwendung, z. B. im Finanzwesen, in der Wirtschaft, bei der Wettervorhersage und bei Umsatzprognosen.
• Genaue Zeitreihenprognosen können Unternehmen helfen, bessere Entscheidungen zu treffen und ihre Gesamtleistung zu verbessern.

Andere Beiträge zum Thema Zeitreihendaten

InfluxDB ist eine optimierte Datenbank für Zeitreihendaten. Du kannst ihre Homepage hier finden.