Ein Konfidenzintervall umfasst eine Reihe von Werten, die mit einer gewissen Wahrscheinlichkeit den wahren Wert eines Parameters beinhalten. Bei diesem Parameter handelt es sich meist um statistische Kennzahlen, wie beispielsweise den Mittelwert oder die Varianz, deren wahrer Wert mit den gegebenen Daten nicht genau berechnet werden kann. Das Konfidenzintervall wird in vielen Fällen aus einer Stichprobe errechnet und besteht aus einer Schätzung für einen Parameter, sowie einer Fehlerspanne, die angibt in welchem Bereich der Messwert auch liegen könnte. Außerdem wird ein Konfidenzniveau angegeben, das aussagt, wie hoch die Wahrscheinlichkeit ist, dass der Messwert in dieser Spanne liegt. 

In diesem Beitrag beschäftigen wir uns mit Konfidenzintervallen und erklären, warum wir überhaupt mit statistischen Schätzungen arbeiten müssen und wie uns Konfidenzintervalle helfen können, diese Unsicherheit auszudrücken. Dazu erklären wir das Konzept anhand eines einfachen Beispiels und zeigen, wie sich das Konfidenzintervall berechnen lässt und wie man es interpretieren kann. Außerdem werden wir die Faktoren beleuchten, die das Intervall beeinflussen, und uns einige Erweiterungen anschauen. 

Warum treten Unsicherheiten in statistischen Schätzungen auf?

In der Statistik entstehen oft Unsicherheiten, da wir mit Stichproben arbeiten müssen, weil es häufig nicht praktikabel oder effizient wäre, die gesamte Population zu befragen, um den wahren Wert herauszubekommen. In vielen Fällen reicht es deshalb aus, eine möglichst repräsentative Menge aus der Population zu befragen und damit eine möglichst genaue Schätzung über die gesuchten Kennzahlen zu machen. 

Angenommen wir wollen herausfinden, wie groß die durchschnittliche Person in New York City ist, dann wäre es nicht wirtschaftlich eine Umfrage durchzuführen, die wirklich jeden gemeldeten Bewohner befragt. Selbst wenn die Mittel dafür vorhanden wären, könnte es außerdem passieren, dass uns ein Teil der Befragten nicht antwortet oder wir eine veraltete Datenbasis haben und dadurch nicht alle Personen erfasst sind. Dies führt dazu, dass wir die tatsächliche, durchschnittliche Körpergröße eines Bewohners von New York City nur sehr schwer herausfinden können. Aus diesem Grund müssen wir auf Stichproben zurückgreifen, sodass wir lediglich eine ausgewählte Menge an Bewohnern befragen, also zum Beispiel 10.000.

Jedoch bestimmt hierbei eine Unsicherheit, dass die durchschnittliche Körpergröße der 10.000 Befragten auch wirklich mit dem tatsächlichen Wert der ganzen Stadt übereinstimmt, weshalb wir auf Wahrscheinlichkeiten zurückgreifen müssen. Es gibt einige Faktoren, welche die Genauigkeit unserer Schätzung erhöhen können, wie zum Beispiel die Stichprobengröße zu erhöhen oder die Datenqualität zu verbessern, indem unter anderem sichergestellt ist, dass alle Stadteile in der Umfrage berücksichtigt wurden. Nichtsdestotrotz bleibt die Unsicherheit ein zentraler Punkt in der statistischen Analyse, welcher quantifiziert und kommuniziert werden muss. Dabei helfen die Konfidenzintervalle, indem sie quantifizieren, wie sicher man sich bei einer Schätzung sein kann. 

Wie ist ein Konfidenzintervall aufgebaut und wie berechnet man es?

Die Basis eines Konfidenzintervalls ist der zentrale Schätzwert, um den sich das Intervall dreht und welcher aus der Stichprobe errechnet wurde. In unserem Fall ist das der Durchschnitt der Körpergröße, welcher aus der Befragung von 10.000 New Yorkern errechnet wurde. 

Als nächstes benötigen wir die Grenzen des Intervalls. Die Fehlerspanne, oder auch der marginale Fehler genannt, gibt an, wie weit der wahre Wert von der Schätzung entfernt sein könnte. Sie gibt also einen Maximal- und einen Minimalwert an, in dem der tatsächliche Wert des Parameters liegen kann. Um dieses Intervall berechnen zu können, werden die folgenden Schritte getätigt: 

1. Berechnung des Standardfehlers

Dieser Wert misst, wie breit die Stichprobenstatistik um den wahren Parameter gestreut ist und berechnet sich mit dieser Formel: 

\(\) \[SE = \frac{s}{\sqrt{n}} \]

Hierbei ist \(s\) die Standardabweichung des Datensatzes und \(n\) die Größe der Stichprobe. Wie man sieht, nimmt der Standardfehler, ab wenn die Standardabweichung niedriger ist, also die Datenpunkte näher beieinander liegen und die Abweichung vom Mittelwert nicht so groß ist. Außerdem nimmt der Standardfehler mit steigender Stichprobengröße ab, da er im Nenner des Bruchs steht. Mit steigender Stichprobengröße decken wir einen größeren Teil der Population ab und Schwankungen in den Daten werden. Meist geringer. 

2. Berechnung der Fehlerspanne

Das sogenannte Konfidenzniveau bestimmt darüber, wie breit das Konfidenzintervall ist. Es gibt eine Aussage darüber, wie sicher wir uns sein können, dass das berechnete Konfidenzintervall auch den wahren Wert des Parameters beinhaltet. Ein Konfidenzniveau von 95% bedeutet zum Beispiel, dass bei 100 zufälligen Stichprobenziehungen 95-mal der wahre Wert des Parameters im Konfidenzintervall liegt und fünfmal außerhalb des Intervalls. Ein höheres Konfidenzniveau steht für eine höhere Sicherheit, dass der wahre Wert im Intervall liegt, sorgt aber dafür, dass das Intervall breiter wird. Um vom Konfidenzniveau zu einem tatsächlichen numerischen Wert zu kommen, wird entweder die z-Verteilung oder die t-Verteilung verwendet, auf deren Unterschiede wir im folgenden Abschnitt noch genauer eingehen. Der entsprechende Wert der Verteilung für das Konfidenzniveau, also zum Beispiel 1,96 bei der z-Verteilung für ein Konfidenzniveau von 95%, wird dann mit dem Standardfehler multipliziert und man erhält die Fehlerspanne: 

\(\)\[ \text{Fehlerspanne} = z \cdot \text{SE} \]

3. Konfidenzintervall bestimmen

Mithilfe der bisher berechneten Werte ergibt sich dann das Konfidenzintervall, indem man den Stichprobenwert berechnet, also zum Beispiel den Mittelwert oder eine andere statistische Kennzahl, und dann die Fehlerspanne, abzieht und auf den Wert addiert, sodass der Stichprobenwert in der Mitte des Konfidenzintervalls liegt. 

Beispiel: 

Angenommen wir haben 10.000 zufällige BewohnerInnen von New York City befragt, wie groß sie sind, und haben dabei einen durchschnittliche Körpergröße von \(\bar{x} = 170cm\) gemessen mit einer Standardabweichung von \(s= 10cm\). Dann können wir daraus den Standardfehler berechnen: 

\(\)\[SE = \frac{s}{\sqrt{n}}\ = \frac{10}{\sqrt{10000}} = 0,1\]

Für unsere Auswertung wählen wir ein Konfidenzniveau von 95 % und nutzen die z-Verteilung mit dem entsprechenden z-Wert von 1,96. Dadurch erhalten wir die Fehlerspanne: 

\(\)\[\text{Fehlerspanne} = z \cdot SE = 1,96 \cdot 0,1 = 0,196 \]

Somit erhalten wir für diese Stichprobe das folgende Konfidenzintervall: 

\(\)\[\bar{x} \pm z \cdot SE = 170 \pm 0,196 \]

Anders geschrieben ergibt sich dann dieser Wertebereich: 

\(\)\[\left[169,804 cm\ ; 170,196 cm\right] \]

Was ist der Unterschied zwischen dem z- und dem t-Wert?

Die z- und t-Verteilung sind zwei unterschiedliche Zufallsverteilungen mit einer ähnlichen Form, die sich jedoch in gewissen Details unterscheiden. Diese Unterscheidungen führen dazu, dass sie für verschiedene Anwendungen genutzt werden sollten. 

Die z-Verteilung, oder auch Standardnormalverteilung, weist einen Mittelwert von 0 auf und eine Standardabweichung von 1. Sie hat die charakteristische, glockenförmige Kurve, welche symmetrisch um die y-Achse verläuft. Die z-Werte sollten für die Konfidenzintervalle verwendet werden, wenn: 

1. Die Stichprobe groß ist, also etwa \(n \geq 30\), denn dann sind die Ergebnisse aufgrund des zentralen Grenzwertsatzes genauer und werden weniger von Zufallsschwankungen beeinflusst. 
2. Die Standardabweichung der gesamten Population bekannt ist. Dies ist ein wichtiges Kriterium, das es uns ermöglicht, die Unsicherheit besser berechnen zu können. 

In vielen Fällen wird der z-Wert für die Bestimmung des Konfidenzintervalls benutzt, da die Werte für die verschiedenen Konfidenzniveaus konstant bleiben und sich nicht mit der Stichprobengröße verändern. 

Die t-Verteilung hat eine ähnliche Form wie die z-Verteilung jedoch mit dem Unterschied, dass es sogenannte „breitere Schwänze“ hat, also der Graph an den Rändern etwas höher liegt. Dies führt dazu, dass extreme Werte in dieser Verteilung wahrscheinlicher sind. Die t-Verteilung verändert sich mit der Größe der Stichprobe und nähert sich mit steigender Stichprobengröße immer stärker der z-Verteilung an, weil dann präzisere Schätzungen möglich sind. 

Die t-Werte sind für die Konfidenzintervalle interessant, wenn die folgenden Bedingungen erfüllt sind: 

1. Die Stichprobe klein ist, also \(n < 30\). Wenn weniger Daten vorhanden sind, ist die Unsicherheit größer und die t-Verteilung sollte verwendet werden. 
2. Die Standardabweichung der gesamten Population nicht bekannt ist. Dadurch sind wir gezwungen, die Standardabweichung der Population aus der Stichprobe abzuschätzen, wodurch die Berechnungen ungenauer werden. 

Wie interpretiert man das Konfidenzniveau und welche Missverständnisse gibt es?

Mithilfe des Konfidenzniveaus wird angegeben, wie zuverlässig die Methode zur Berechnung des Konfidenzintervalls wirklich ist. Dies ist jedoch nicht damit gleichzusetzen, wie sicher wir über ein konkretes Intervall sind. 

Bei einem Konfidenzniveau von 95% sprechen wir davon, dass bei wiederholter Erstellung von Stichproben und auch einer erneuten Berechnung des Konfidenzintervalls in 95 von 100 Fällen der wahre Wert im berechneten Intervall liegt. Die Wahrscheinlichkeit von 95% gibt also nicht an, dass der wahre Wert mit einer 95-prozentigen Wahrscheinlichkeit innerhalb des Intervalls liegt. Das Intervall ist fest und der Wert kann entweder darin liegen oder nicht. Hinzu kommen auch die folgenden Missverständnisse, die häufig bei der Interpretation des Konfidenzniveaus aufkommen: 

1. „95% der Daten liegen im Konfidenzintervall.“: Ein Konfidenzintervall gibt keine direkte Aussage über die Verteilung der Daten, sondern lediglich über die Schätzung eines Parameters, wie zum Beispiel den Mittelwert oder die Varianz. Es kann sowohl passieren, dass viele Daten innerhalb des Intervalls als auch außerhalb des Intervalls liegen, da sich das Intervall lediglich auf den geschätzten Parameter bezieht. 
2. „Der wahre Wert liegt mit einer Wahrscheinlichkeit von 95% im Intervall.“: Der wahre Wert des Parameters ist unbekannt und kann entweder im Intervall oder außerhalb des Intervalls liegen. Die Wahrscheinlichkeit bezieht sich auf die Unsicherheit, ob die Methode korrekte Intervalle liefert und nicht auf den Wert selbst. Somit ist diese Aussage streng genommen nicht richtig, da der wahre Wert des Parameters keine Zufallsgröße ist und somit nicht stochastisch ist. Die obere und untere Grenze des Konfidenzintervalls sind hingegen stochastisch. Man trifft diese Formulierung jedoch in der Realität sehr häufig an (so wie auch in diesem Beitrag).
3. „Ein breites Konfidenzintervall ist schlechter als ein schmales.“: Ein breiteres Intervall entsteht häufig bei einer größeren Unsicherheit im Datensatz, also bei einer höheren Standardabweichung oder einer kleinen Stichprobe. Es ist jedoch auch ehrlicher als ein schmales Intervall, welches möglicherweise die Unsicherheit unterschätzt.
4. „Ein einzelnes Intervall garantiert Genauigkeit.“: Das Konfidenzniveau bezieht sich auf die langfristige Genauigkeit der Methode zur Intervallberechnung und nicht auf ein einzelnes Intervall. Selbst bei einem hohen Konfidenzniveau kann es passieren, dass der wahre Wert nicht innerhalb des Konfidenzintervalls liegt. Unabhängig vom Konfidenzniveau bleibt die statistische Unsicherheit gegeben. 

Das Konfidenzniveau beschreibt die Sicherheit der Methode und sollte nicht verwechselt werden mit der Wahrscheinlichkeit, dass der wahre Wert innerhalb des Intervalls liegt. 

Welche Erweiterungen gibt es bei Konfidenzintervallen?

Die Konfidenzintervalle sind ein wichtiges Werkzeug in der Statistik, weshalb sich über die Zeit verschiedene Anwendungen und Methoden entwickelt haben, die auf diesen Intervallen basieren oder sie so verändern, dass sie auch für nicht normalverteilte Daten genutzt werden können. In diesem Abschnitt gehen wir auf die wichtigsten Erweiterungen der Konfidenzintervalle ein, um die Anpassungsfähigkeit und Vielseitigkeit dieser Methode aufzuzeigen. 

Einseitige vs. Zweiseitige Intervalle

Allgemein formuliert definiert das Konfidenzintervall einen Wertebereich in dem der wahre Wert eines Parameters, wie zum Beispiel der Mittelwert oder die Varianz, liegt. Abhängig von der Fragestellung unterscheidet man zweiseitige Intervalle, bei denen beide Abweichungsrichtungen vom geschätzten Wert berücksichtigt werden, und einseitige Intervalle, bei denen nur eine Abweichungsrichtung in Frage kommt: 

• Zweiseitige Intervalle: Bei zweiseitigen Intervallen liegt der geschätzte Wert des Parameters mittig im Konfidenzintervall und es ist möglich, dass der wahre Wert kleiner oder größer als der geschätzte Wert ist. Bei unserem vorherigen Beispiel zur Abschätzung der durchschnittlichen Körpergröße in New York City beispielsweise kann der wahre Durchschnitt sowohl größer sein als der geschätzte Wert von 170cm, er kann aber auch kleiner sein. In unserem Beispiel ergab sich also ein Intervall mit den folgenden Grenzen: [169,804cm; 170,196cm]. Zweiseitige Intervall werden vor allem dann verwendet, wenn es keine spezifische Vermutung über die Richtung der Abweichung gibt und somit beide Richtungen in die Abschätzung mit einbezogen werden sollen. Die Berechnung des zweiseitigen Konfidenzintervalls funktioniert im Detail wie oben beschrieben und lässt sich mit der folgenden Formel gut zusammenfassen: 

\(\)\[\bar{x} \pm z\cdot SE = \bar{x} \pm z \cdot \frac{s}{\sqrt{n}} \]

• Einseitige Intervalle: Bei einseitigen Konfidenzintervallen wird hingegen nur eine Abweichungsrichtung vom geschätzten Wert betrachtet, sodass nur Werte, welche größer sind, oder nur Werte, welche kleiner sind, in das Intervall mit einbezogen werden. In der Anwendung machen einseitige Intervalle vor allem dann Sinn, wenn wir nur an einer Abweichungsrichtung interessiert sind, da Grenzwerte oder Sicherheitsstandards eingehalten werden müssen. Beispielsweise könnte es bei einer Maschine sinnvoll sein, dass diese maximal 100 Einheiten in der Stunde produziert, da ansonsten nicht genügend Rohstoffe nachgeliefert werden können. Somit sollte das Konfidenzintervall unter 100 liegen und eine Abweichung nach oben ist nicht zulässig. Das Konfidenzintervall berechnet sich in diesem Fall sehr ähnlich zum zweiseitigen Fall: 

\(\)\[\bar{x} – z \cdot SE = \bar{x} – z \cdot \frac{s}{\sqrt{n}}\]

Wichtig ist hierbei jedoch zu beachten, dass der z-Wert für einseitige Intervalle nicht derselbe ist wie bei einem zweiseitigen Intervall, auch dann, wenn das Konfidenzniveau identisch ist. Für ein Konfidenzniveau von 95% zum Beispiel ist z-Wert für ein zweiseitiges Intervall 1,96 und für einen einseitiges Intervall 1,65.

Hypothesentests

Konfidenzintervalle und Hypothesentests sind zwei eng miteinander verbundene Konzepte innerhalb der Statistik, welche genutzt werden, um belastbare Aussagen über die Schätzung von Parametern treffen zu können. Während der Hypothesentest an sich nur prüft, ob ein spezifischer Wert plausibel ist, erhält er mithilfe des Konfidenzintervalls eine breitere Perspektive, da man sieht, ob die Hypothese innerhalb des Intervalls liegt oder nicht. 

Um das Vorgehen genauer zu verstehen, betrachten wir das Beispiel eines Unternehmens, welches Batterien herstellt. Das Unternehmen behauptet, dass die von ihnen produzierten Batterien im Durchschnitt eine Laufzeit von 50 Stunden haben. Es stellt also die sogenannte Nullhypothese auf, dass der wahre Mittelwert aller ihrer Batterien 50 Stunden beträgt, also \(H_0: \mu = 50 \). Da es nicht möglich ist, alle jemals produzierten Batterien zu untersuchen, schauen wir uns eine Stichprobe von 30 Produkten genauer an, für die wir die Lebensdauer bestimmen. Das Ziel des Hypothesentests ist es nun herauszufinden, ob die Stichprobe die Hypothese über den wahren Wert unterstützt oder nicht. 

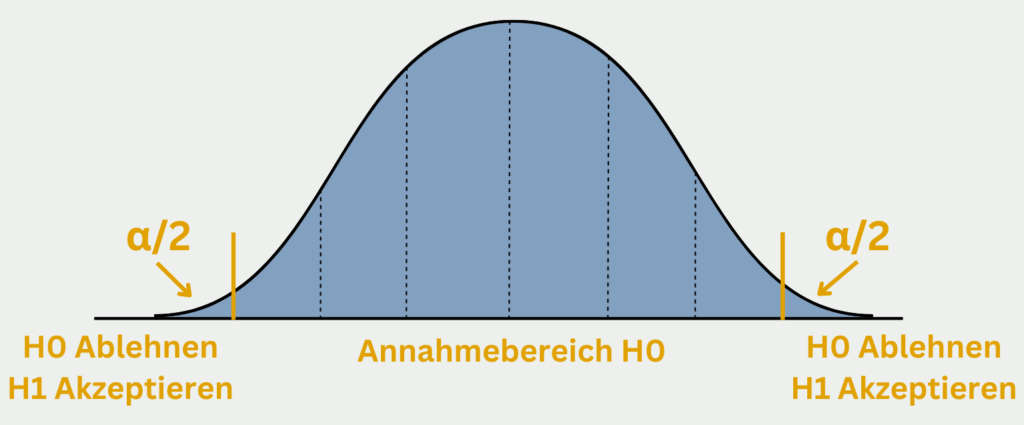
Angenommen das Konfidenzintervall unserer Stichprobe liegt mit einem Konfidenzniveau von 95% zwischen 45 und 49 Stunden. Wie wir nun gelernt haben, bedeutet das Konfidenzintervall, dass bei 100 Stichproben 95mal ein Intervall gebildet wird, welches den wahren Wert inkludiert. Wie wir feststellen, liegt die Hypothese des Unternehmens, also ein Durchschnittswert von 50 Stunden, nicht in diesem Intervall, sodass wir die Nullhypothese mit einem Signifikanzniveau von fünf Prozent ablehnen können. Vielmehr ist es wahrscheinlicher, dass die tatsächliche durchschnittliche Lebensdauer leicht unter 50 Stunden liegt. 

Die Konfidenzintervalle sind ein wichtiges Werkzeug bei der Überprüfung von Hypothesen, da sie im Gegensatz zu reinen Wahrscheinlichkeitswerten auch Informationen über die Präzision des Ergebnisses geben und das wahrscheinliche Intervall definieren, in dem der tatsächliche Wert vermutlich liegt. Dadurch erhöht sich die Interpretationsfähigkeit und das Verfahren wird deutlich intuitiver. 

Bootstrapping

Abhängig von der Anwendung kann es passieren, dass die Grundannahmen der Konfidenzintervalle nicht gegeben sind, also zum Beispiel die Daten keine Normalverteilung darstellen. Dies kann bei sehr kleinen Stichproben schnell passieren. Statt trotzdem von einer Normalverteilung auszugehen, nutzen wir die sogenannte Bootstrapping-Methode und generieren künstliche Stichproben, um die Verteilung des Parameters abzuschätzen. Dazu wird aus dem Topf der vorhandenen Datenpunkte zufällig ein Wert gezogen und dieser wird danach wieder zurückgelegt. Daraus kann dann eine neue Stichprobe mit beliebiger Größe erstellt werden. 

Angenommen wir untersuchen die durchschnittliche Schlafdauer von verschiedenen Probanden, haben jedoch nur eine Stichprobe von zehn Personen, mit denen wir trotzdem das Konfidenzintervall für den Durchschnittswert errechnen wollen. Dazu ziehen wir tausend Mal zufällig eine der zehn Personen aus dem „Topf“ und speichern diese in einer neuen Stichprobe ab. Danach legen wir den Probanden wieder in den „Topf“ zurück, sodass dieselbe Person theoretisch auch zweimal hintereinander gezogen werden können. Mit diesem neuen Datensatz aus tausend Personen, den wir künstlich aus lediglich zehn Personen erstellt haben, können wir wie gewohnt ein Konfidenzintervall und einen geschätzten Parameter errechnen. 

Die Bootstrapping-Methode bietet sich nicht nur bei sehr kleinen Stichproben an, sondern kann beispielsweise auch verwendet werden, wenn die Daten asymmetrisch sind, anderweitig verteilt sind oder sich keine Aussage über eine mögliche Verteilung treffen lässt. Durch den Bootstrapping-Algorithmus erhält der künstliche Datensatz eine Normalverteilung, da das Prinzip vom „Ziehen und Zurücklegen“ einer Normalverteilung folgt. 

Das solltest Du mitnehmen

• Das Konfidenzintervall definiert einen Wertebereich um einen geschätzten Parameter aus einer Stichprobe, welcher mit einer gewissen Wahrscheinlichkeit, den tatsächlichen Parameter der Population enthält. 
• Dabei können einseitige Intervalle, welche nur Abweichungen in eine Richtung zulassen, und zweiseitige Intervalle, welche Abweichungen in beide Richtungen zulassen, bestimmt werden. 
• Der z-Wert wird bei der Berechnung der Fehlerspanne genutzt, wenn eine ausreichend große Stichprobe gegeben ist und die Standardabweichung der Population bekannt ist. Wenn eines dieser Merkmale nicht erfüllt ist, sollte auf den t-Wert zurückgegriffen werden. 
• Das Konfidenzintervall spielt vor allem bei Hypothesentests eine wichtige Rolle, da es diese Methode intuitiver macht, indem es nicht nur eine Aussage darüber gibt, ob die Hypothese abgelehnt wird oder nicht, sondern auch den Wertebereich mitliefert. 
• Mithilfe von Bootstraping können Konfidenzintervalle auch für sehr kleine Stichproben oder asymmetrische Datenverteilungen berechnet werden. 

Andere Beiträge zum Thema Konfidenzintervalle

Die Universität Yale bietet einen ausführlichen Artikel zu diesem Thema.