Modelle mit Nullen sind eine Art von statistischen Modellen, die zur Analyse von Datensätzen mit einer übermäßigen Anzahl von Nullwerten verwendet werden. Diese Zero-Inflated Models werden häufig auf Datensätze angewandt, bei denen eine bestimmte Antwortvariable häufig Null ist, aber auch durch einen separaten Prozess erzeugt wird, der Nicht-Null-Werte erzeugen kann.

Dieses Phänomen wird als Null-Inflation bezeichnet und kann aus verschiedenen Gründen auftreten, z. B. Messfehler, Stichprobenverzerrungen oder biologische Prozesse. Null-Inflations-Modelle schätzen die Wahrscheinlichkeit der Null-Inflation und der zugrunde liegenden Nicht-Null-Verteilung, um solche Daten genauer zu modellieren. Dieser Artikel befasst sich mit den Grundlagen von Null-Inflationsmodellen, ihren Arten, Anwendungen und Herausforderungen.

Was ist ein Zero-Inflated Model?

Ein Nullwertmodell ist ein statistisches Modell, das zur Analyse von Daten verwendet wird, bei denen die Antwortvariable eine übermäßige Anzahl von Nullwerten aufweist, verglichen mit dem, was in einer typischen Verteilung erwartet wird. Es handelt sich um ein Zweikomponenten-Mischmodell, das aus einer binären Komponente, die die überschüssigen Nullen modelliert, und einer Zählkomponente besteht, die die Nicht-Null-Zahlen modelliert. Die binäre Komponente modelliert die Wahrscheinlichkeit, eine Null zu beobachten, während die Zählkomponente die Verteilung der Nicht-Null-Werte modelliert.

Die Hauptannahme eines Modells mit Nullen ist, dass die überschüssigen Nullen nicht auf eine zufällige Variation zurückzuführen sind, sondern auf einen separaten Prozess. Dieser separate Prozess kann auf Faktoren wie einen zugrunde liegenden Krankheitszustand oder Umweltfaktoren zurückzuführen sein, die den Messprozess beeinflussen. Nullwertmodelle können für eine Vielzahl von Antwortvariablen verwendet werden, einschließlich kontinuierlicher, diskreter und ereignisbezogener Daten.

Was ist die Null-Inflation?

Nullinflation ist ein Phänomen, das auftritt, wenn ein Datensatz eine ungewöhnlich hohe Anzahl von Nullwerten aufweist, verglichen mit dem, was bei einer Standardverteilung zu erwarten wäre. Das Verständnis und die Behandlung von Null-Inflation ist für eine genaue statistische Modellierung und Analyse unerlässlich. In diesem Abschnitt werden das Konzept der Nullinflation, ihre möglichen Ursachen und Ansätze zur Modellierung und Behandlung dieses Phänomens untersucht.

Nullinflation kann durch strukturelle Faktoren, die dem Datenerzeugungsprozess inhärent sind, oder durch Stichprobenfaktoren im Zusammenhang mit der Datenerhebung oder -messung entstehen. Zu den strukturellen Faktoren können bestimmte Merkmale der untersuchten Phänomene gehören, bei denen ein signifikanter Anteil der Beobachtungen naturgemäß Null sein dürfte. Stichprobenfaktoren hingegen können auf Einschränkungen oder Fehler bei der Datenerhebung zurückzuführen sein, die zu einer übermäßigen Anzahl von Nullwerten führen.

Um die Merkmale der Null-Inflation zu erfassen, werden spezifische statistische Modelle verwendet. Zwei gängige Arten von Modellen, die in diesem Zusammenhang verwendet werden, sind Null-Inflations-Modelle und Null-veränderte Modelle. Modelle mit Nullen gehen von einem zweiteiligen Prozess aus, wobei ein Teil Nullen und ein anderer Teil Nicht-Null-Werte erzeugt. Im Gegensatz dazu gehen Modelle mit veränderten Nullen davon aus, dass Nullwerte aufgrund eines separaten Prozesses entstehen, wobei der Anteil der Nullen nicht berücksichtigt wird.

Bei der Modellierung der Null-Inflation muss je nach Art der Daten und der Forschungsfrage ein geeigneter Ansatz gewählt werden. Zu diesem Zweck werden in der Regel Null-Inflations-Poisson-Modelle (ZIP) und Null-Inflations-Negativ-Binomial-Modelle (ZINB) verwendet. Diese Modelle schätzen die Wahrscheinlichkeit eines Nullwerts getrennt von der Modellierung der Verteilung der Nicht-Nullwerte und ermöglichen so eine genauere Darstellung der Daten.

Der Umgang mit der Null-Inflation erfordert sorgfältige Überlegungen. Forscher können alternative Datenerhebungsmethoden untersuchen, Datentransformationen vornehmen oder spezielle Modellierungstechniken anwenden. Es ist von entscheidender Bedeutung, die Angemessenheit des gewählten Modells zu bewerten, seine Annahmen zu validieren und die Ergebnisse entsprechend zu interpretieren.

Was sind die verschiedenen Arten von Zero-Inflated Models?

Es gibt zwei Haupttypen von Null-Inflations-Modellen: Null-Inflations-Poisson-Modelle (ZIP) und Null-Inflations-Negativ-Binomial-Modelle (ZINB).

• Null-inflationierte Poisson-Modelle (ZIP): Das ZIP-Modell geht davon aus, dass die beobachteten Daten durch zwei verschiedene Prozesse erzeugt werden: einen, der die Nullwerte erzeugt, und einen, der die positiven Werte erzeugt. Es wird davon ausgegangen, dass die Wahrscheinlichkeit eines Nullergebnisses durch einen separaten Bernoulli-Prozess erzeugt wird, der ein binärer Prozess ist, der Ergebnisse erzeugt, die entweder Erfolg oder Misserfolg sind. Die Erfolgswahrscheinlichkeit dieses Bernoulli-Prozesses wird mit p bezeichnet, und die Misserfolgswahrscheinlichkeit ist (1-p). Wenn der Bernoulli-Prozess fehlschlägt, wird die Antwortvariable aus einer Poisson-Verteilung mit Mittelwert λ generiert. Wenn der Bernoulli-Prozess erfolgreich ist, ist die Antwortvariable immer Null.
• Null-inflationäre negative Binomialmodelle (ZINB): Das ZINB-Modell ähnelt dem ZIP-Modell insofern, als es ebenfalls davon ausgeht, dass die beobachteten Daten aus zwei verschiedenen Prozessen stammen. Der Unterschied besteht jedoch darin, dass das ZINB-Modell davon ausgeht, dass die Nicht-Null-Werte aus einer negativen Binomialverteilung anstelle einer Poisson-Verteilung generiert werden. Die negative Binomialverteilung ist eine Verallgemeinerung der Poisson-Verteilung, die eine Überdispersion zulässt, was bedeutet, dass die Varianz größer sein kann als der Mittelwert. Die Wahrscheinlichkeit eines Nullergebnisses wird immer noch aus einem separaten Bernoulli-Prozess generiert, genau wie im ZIP-Modell.

Sowohl ZIP- als auch ZINB-Modelle können zur Modellierung von Zähldaten mit überzähligen Nullen verwendet werden, wie z. B. die Zahl der Arztbesuche oder die Zahl der Unfälle am Arbeitsplatz. Diese Modelle werden häufig in vielen Bereichen verwendet, z. B. im Gesundheitswesen, in den Sozialwissenschaften, in der Ökologie und in der Wirtschaft.

Wie interpretiert man die Parameter eines Nullwertmodells?

Bei der Interpretation von Modellen mit Nullen geht es darum, die geschätzten Parameter und ihre Auswirkungen im Zusammenhang mit den in den Daten beobachteten übermäßigen Nullen zu verstehen. Hier sind die wichtigsten Punkte, die bei der Interpretation von Modellen mit Inflationsfreiheit zu beachten sind:

• Null-Inflations-Komponente: Die Null-Inflations-Komponente des Modells stellt den zusätzlichen Prozess dar, der übermäßige Nullen erzeugt. Sie wird in der Regel durch die Wahrscheinlichkeit überschüssiger Nullen (π) beschrieben, die die Wahrscheinlichkeit angibt, dass ein Nullwert aufgrund des Null erzeugenden Prozesses beobachtet wird. Ein höheres π zeigt eine größere Neigung zu überzähligen Nullen in den Daten an.
• Zählkomponente: Die Zählkomponente des Modells stellt die Verteilung der Nicht-Null-Werte dar. Sie wird häufig mit einer Wahrscheinlichkeitsverteilung wie der Poisson- oder der negativen Binomialverteilung modelliert. Die Parameter dieser Komponente geben Aufschluss über die Intensität oder Häufigkeit des Auftretens von Nicht-Null-Werten.
• Odds Ratios oder Rate Ratios: In Modellen mit Null-Inflation werden Odds Ratios oder Rate Ratios üblicherweise zur Interpretation der Auswirkungen von Prädiktorvariablen verwendet. Diese Verhältnisse vergleichen die Chancen oder Raten der Beobachtung von Nicht-Null-Werten zwischen verschiedenen Niveaus einer Prädiktorvariablen. Ein Verhältnis größer als 1 deutet auf eine höhere Wahrscheinlichkeit von Nicht-Null-Werten hin, während ein Verhältnis kleiner als 1 auf eine geringere Wahrscheinlichkeit hinweist.
• Erläuternde Variablen: Die Auswirkungen der erklärenden Variablen in Modellen mit Inflationsfreiheit können sowohl in Bezug auf die Null-Inflations- als auch auf die Zählkomponenten interpretiert werden. Bei der Null-Inflationskomponente können die Variablen den Prozess der überzähligen Nullen beeinflussen, was auf Faktoren hinweist, die zu Nullwerten beitragen. Bei der Zählkomponente wirken sich die Variablen auf die Rate oder Intensität der Nicht-Null-Werte aus, was auf Faktoren hinweist, die die Häufigkeit oder das Ausmaß der beobachteten Ereignisse beeinflussen.
• Substanzielle Interpretation: Die Interpretation von Modellen mit Nullwerten geht über die statistische Signifikanz hinaus. Sie erfordert ein inhaltliches Verständnis der Daten und des Kontextes der Analyse. Berücksichtigen Sie die spezifische Forschungsfrage und ziehen Sie sinnvolle Schlussfolgerungen auf der Grundlage der geschätzten Parameter und der damit verbundenen Unsicherheiten.
• Modellanpassung und Anpassungsgüte (Goodness of Fit): Die Bewertung der Anpassungsgüte ist von entscheidender Bedeutung, um die Gültigkeit des Nullmodells sicherzustellen. Bewerten Sie Diagnosemaßnahmen wie Residualanalyse, Modellvergleichsverfahren und Anpassungsgütetests, um festzustellen, ob das Modell die Muster und die Variabilität in den Daten angemessen wiedergibt.
• Sensitivitätsanalyse: Führen Sie Sensitivitätsanalysen durch, um die Robustheit der Interpretation zu bewerten. Untersuchen Sie verschiedene Modellspezifikationen, alternative Verteilungen oder den Einschluss bzw. Ausschluss von Variablen, um die Stabilität und Konsistenz der Ergebnisse zu bewerten.

Durch eine sorgfältige Interpretation der geschätzten Parameter, das Verständnis der Auswirkungen der Null-Inflationskomponente und die Berücksichtigung der Auswirkungen von Prädiktorvariablen können Forscher Einblicke in die Faktoren gewinnen, die die übermäßigen Nullen in den Daten verursachen. Dies ermöglicht ein tieferes Verständnis der zugrunde liegenden Prozesse und erleichtert eine fundiertere Entscheidungsfindung in verschiedenen Studienbereichen.

Was sind die Vor- und Nachteile von Zero-Inflated Models?

Modelle mit Nullen sind in verschiedenen Bereichen weit verbreitet, z. B. in der Epidemiologie, den Wirtschaftswissenschaften und der Umweltwissenschaft, da sie Daten mit übermäßigen Nullen verarbeiten können. Wie jedes statistische Modell haben jedoch auch Nullwertmodelle ihre eigenen Vor- und Nachteile. In diesem Abschnitt werden einige der wichtigsten Vorteile und Einschränkungen der Verwendung von Modellen mit Nullen für die Datenanalyse erörtert.

Vorteile:

• Nullwertmodelle ermöglichen die Modellierung von Datensätzen mit überschüssigen Nullwerten, was mit traditionellen Modellen nicht möglich wäre.
• Sie können genauere Vorhersagen bei Datensätzen mit einem hohen Anteil an Nullwerten liefern.
• Sie können zur Identifizierung und Unterscheidung zwischen echten Nullwerten und Nullwerten, die auf einen Überschuss an Nullen im Datensatz zurückzuführen sind, verwendet werden.

Nachteile:

• Modelle mit Nullen können rechenintensiv sein und erfordern im Vergleich zu herkömmlichen Modellen mehr Zeit und Ressourcen für die Anpassung.
• Sie erfordern einen größeren Stichprobenumfang, um zuverlässige Parameterschätzungen zu erhalten.
• Die Interpretation der Ergebnisse kann komplex sein und erfordert unter Umständen Fachkenntnisse in statistischer Modellierung.
• Wenn die Daten nicht wirklich null-inflationär sind, kann die Verwendung eines Zero-Inflated Models zu einem Overfitting und potenziell verzerrten Ergebnissen führen.

Welche Anwendungen gibt es für Nullwertmodelle?

Modelle mit Null-Inflation haben mehrere Anwendungen in verschiedenen Bereichen. Hier sind einige Beispiele:

• Gesundheitswesen: Im Gesundheitswesen werden Zero-Inflated Models verwendet, um die Häufigkeit von Krankenhausaufenthalten und die Anzahl der Besuche in der Notaufnahme zu untersuchen. Diese Modelle können den Leistungserbringern im Gesundheitswesen helfen, die Faktoren zu verstehen, die zu diesen Ergebnissen beitragen, was wiederum als Grundlage für Maßnahmen zur Verringerung von Krankenhausaufenthalten und Besuchen in der Notaufnahme dienen kann.
• Ökologie: In der Ökologie werden Nullwertmodelle verwendet, um die Verteilung von Arten in einem bestimmten Ökosystem zu untersuchen. Durch das Verständnis der Faktoren, die zum Vorhandensein oder Fehlen einer bestimmten Art beitragen, können Forscher Strategien zum Schutz gefährdeter Arten und zur Erhaltung von Ökosystemen entwickeln.
• Wirtschaftswissenschaften: In den Wirtschaftswissenschaften werden Zero-Inflated Models verwendet, um die Nachfrage nach Waren und Dienstleistungen zu untersuchen. Durch das Verständnis der Faktoren, die zu einer Nullnachfrage beitragen, können Unternehmen Strategien zur Steigerung der Nachfrage und zur Gewinnmaximierung entwickeln.
• Marketing: Im Marketing werden Nullwertmodelle verwendet, um das Kundenverhalten zu untersuchen. Durch das Verständnis der Faktoren, die zu Nullkäufen beitragen, können Unternehmen Strategien entwickeln, um den Absatz zu steigern und die Kundenbindung zu verbessern.

Insgesamt können Modelle mit Nullkäufen in jedem Bereich angewendet werden, in dem Zähldaten gesammelt werden und eine hohe Häufigkeit von Nullkäufen vorliegt. Diese Modelle können Forschern und Praktikern helfen, die Faktoren zu verstehen, die zu diesen Nullzählungen beitragen, und so Strategien zur Verbesserung der Ergebnisse zu entwickeln.

Wie erstellt man ein Zero-Inflated Models in Python an?

Die Anpassung von Modellen mit Nullwerten kann mit verschiedenen statistischen Softwarepaketen durchgeführt werden, darunter R, SAS und Python. Ein beliebtes Python-Paket für die Anpassung von Nullwertmodellen ist statsmodels. Hier ist ein Beispiel für die Anpassung eines zero-inflated Modells mit

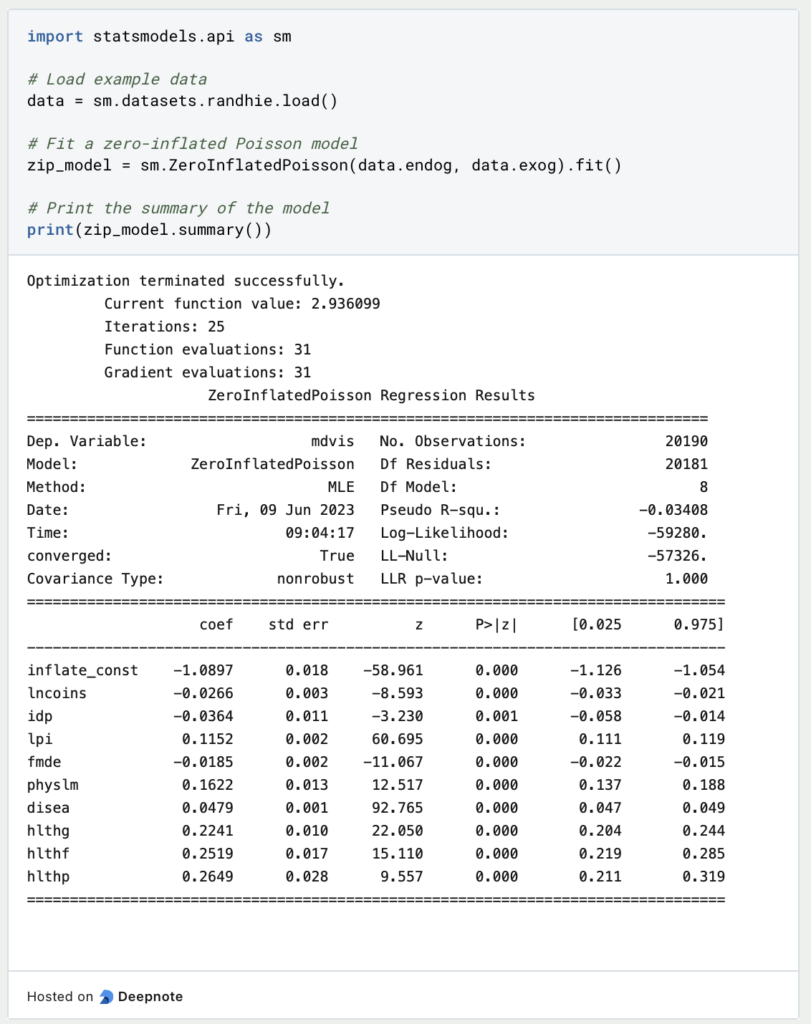
In diesem Beispiel haben wir einen Beispieldatensatz aus statsmodels geladen und ein null-inflationäres Poisson-Modell mit der Klasse ZeroInflatedPoisson angepasst. Die endog-Variable steht für die Antwortvariable und die exog-Variable für die erklärenden Variablen. Nach der Anpassung des Modells haben wir mit der Methode summary() eine Zusammenfassung der Ergebnisse ausgegeben. Diese Zusammenfassung enthält Informationen wie die Koeffizienten, Standardfehler und p-Werte für jede Variable des Modells.

Beachte, dass es in statsmodels mehrere andere Klassen für die Anpassung verschiedener Typen von Modellen mit Null-Inflation gibt, darunter ZeroInflatedNegativeBinomial, ZeroInflatedBinomial und ZeroInflatedGeneralizedPoisson. Die Syntax für die Anpassung dieser Modelle ähnelt dem obigen Beispiel, aber die spezifische Klasse und die Argumente variieren je nach dem Typ des Modells, das Sie anpassen möchten.

Das solltest Du mitnehmen

• Nullwertmodelle sind eine Art von statistischen Modellen, die mit übermäßigen Nullen in Zähldaten umgehen können.
• Sie sind nützlich in Situationen, in denen es einen Überschuss an Nullen im Vergleich zu dem gibt, was zufällig zu erwarten wäre.
• Die beiden Arten von Zero-Inflated Models sind das Null-Inflations-Poisson-Modell (ZIP) und das Null-Inflations-Negativ-Binomial-Modell (ZINB).
• Zu den Vorteilen von Nullwertmodellen gehören ihre Fähigkeit, mit Überstreuung und übermäßigen Nullen umzugehen, während zu den Nachteilen die Annahme gehört, dass der Prozess der Nulleninflation unabhängig vom Zählprozess ist.
• Nullinflationsmodelle finden in vielen Bereichen Anwendung, z. B. in der Epidemiologie, Ökologie und im Marketing.
• Die Anpassung eines Null-Inflationsmodells umfasst die Identifizierung des geeigneten Modells, die Schätzung der Parameter und die Bewertung der Anpassungsgüte.
• Python bietet verschiedene Pakete wie statsmodels und Scikit-learn, die für die Anpassung von Modellen mit Null-Inflation verwendet werden können.

Andere Beiträge zum Thema Zero-Inflated Models

Die University of Otago hat ein interessantes Skript zu Nullwertmodellen mit vielen Beispielen. Die Folien sind hier zu finden.