Zero-inflated models are a type of statistical model used to analyze data sets with an excessive number of zero values. These models are often applied to data sets where a particular response variable is frequently zero but is also generated by a separate process that can produce non-zero values.

This phenomenon is known as zero inflation and can occur for various reasons such as measurement error, sampling bias, or biological processes. Zero-inflated models estimate the probability of zero inflation and the underlying non-zero distribution to more accurately model such data. This article will cover the basics of zero-inflated models, their types, applications, and challenges.

What is a zero-inflated Model?

A zero-inflated model is a type of statistical model used to analyze data where the response variable has an excessive number of zero values compared to what is expected in a typical distribution. It is a two-component mixture model consisting of a binary component that models the excess zeros and a count component that models the non-zero counts. The binary component models the probability of observing a zero, while the count component models the distribution of the non-zero values.

The main assumption of a zero-inflated model is that the excess zeros are not due to random variation, but rather a separate process. This separate process may be due to factors such as an underlying disease state or environmental factors affecting the measurement process. Zero-inflated models can be used for a variety of response variable types, including continuous, discrete, and time-to-event data.

What is Zero Inflation?

Zero inflation is a phenomenon that occurs when a dataset exhibits an unusually high number of zero values compared to what would be expected in a standard distribution. Understanding and addressing zero inflation is essential for accurate statistical modeling and analysis. This section explores the concept of zero inflation, its potential causes, and approaches to modeling and dealing with this phenomenon.

Zero inflation can arise due to structural factors inherent in the data-generating process or sampling factors related to data collection or measurement. Structural factors may include certain characteristics of the phenomena being studied, where a significant proportion of the observations are naturally expected to be zero. Sampling factors, on the other hand, can result from limitations or errors in data collection, leading to an excessive number of zero values.

To capture the characteristics of zero inflation, specific statistical models are employed. Two common types of models used in this context are zero-inflated models and zero-altered models. Zero-inflated models assume a two-part process, with one part generating zeros and another part generating non-zero values. On the other hand, zero-altered models assume that zero values occur due to a separate process but do not account for the proportion of zeros.

Modeling zero inflation involves selecting an appropriate approach based on the nature of the data and research question. Zero-inflated Poisson (ZIP) and zero-inflated negative binomial (ZINB) models are commonly used for this purpose. These models estimate the probability of a zero value separately from modeling the distribution of non-zero values, allowing for a more accurate representation of the data.

Dealing with zero inflation requires careful consideration. Researchers may explore alternative data collection methods, employ data transformations, or use specialized modeling techniques. It is crucial to assess the adequacy of the selected model, validate its assumptions, and interpret the results accordingly.

What are the different types of zero-inflated models?

There are two main types of zero-inflated models: zero-inflated Poisson (ZIP) models and zero-inflated negative binomial (ZINB) models.

1. Zero-inflated Poisson (ZIP) models: The ZIP model assumes that the observed data are generated from two different processes: one that generates the zero values and one that generates the positive values. The probability of a zero outcome is assumed to be generated from a separate Bernoulli process, which is a binary process that generates outcomes that are either success or failure. The probability of success in this Bernoulli process is denoted as p, and the probability of failure is (1-p). If the Bernoulli process fails, then the response variable is generated from a Poisson distribution with mean λ. If the Bernoulli process succeeds, then the response variable is always zero.
2. Zero-inflated negative binomial (ZINB) models: The ZINB model is similar to the ZIP model in that it also assumes that the observed data come from two different processes. However, the difference is that the ZINB model assumes that the non-zero values are generated from a negative binomial distribution instead of a Poisson distribution. The negative binomial distribution is a generalization of the Poisson distribution that allows for overdispersion, which means that the variance can be larger than the mean. The probability of a zero outcome is still generated from a separate Bernoulli process, just like in the ZIP model.

Both ZIP and ZINB models can be used to model count data with excess zeros, such as the number of medical visits or the number of accidents in a workplace. These models are commonly used in many fields, including healthcare, social sciences, ecology, and economics.

How do you interpret the parameters of a zero-inflated model?

Interpreting zero-inflated models involves understanding the estimated parameters and their implications in the context of the excessive zeros observed in the data. Here are key points to consider when interpreting zero-inflated models:

1. Zero-Inflation Component: The zero-inflation component of the model represents the additional process that generates excess zeros. It is typically described by the probability of excess zeros (π), which indicates the likelihood of observing a zero value due to the zero-generating process. A higher π indicates a greater propensity for excess zeros in the data.
2. Count Component: The count component of the model represents the distribution of non-zero values. It is often modeled using a probability distribution such as Poisson or negative binomial. The parameters of this component provide insights into the intensity or rate of occurrence for non-zero values.
3. Odds Ratios or Rate Ratios: In zero-inflated models, odds ratios or rate ratios are commonly used to interpret the effects of predictor variables. These ratios compare the odds or rates of observing non-zero values between different levels of a predictor variable. A ratio greater than 1 suggests a higher likelihood of non-zero values, while a ratio less than 1 indicates a lower likelihood.
4. Explanatory Variables: The effects of explanatory variables in zero-inflated models can be interpreted in relation to both the zero-inflation and count components. For the zero-inflation component, variables may influence the excess zeros process, indicating factors that contribute to zero values. In the count component, variables affect the rate or intensity of non-zero values, indicating factors that impact the frequency or magnitude of observed events.
5. Substantive Interpretation: Interpreting zero-inflated models goes beyond statistical significance. It requires a substantive understanding of the data and the context of the analysis. Consider the specific research question and draw meaningful conclusions based on the estimated parameters and their associated uncertainties.
6. Model Fit and Goodness of Fit: Assessing the goodness of fit is essential to ensure the validity of the zero-inflated model. Evaluate diagnostic measures such as residual analysis, model comparison techniques, and goodness-of-fit tests to determine if the model adequately captures the patterns and variability in the data.
7. Sensitivity Analysis: Conduct sensitivity analyses to evaluate the robustness of the interpretation. Explore different model specifications, alternative distributions, or inclusion/exclusion of variables to assess the stability and consistency of the results.

By carefully interpreting the estimated parameters, understanding the implications of the zero-inflation component, and considering the effects of predictor variables, researchers can gain insights into the factors driving the excessive zeros in the data. This enables a deeper understanding of the underlying processes and facilitates more informed decision-making in various fields of study.

What are the advantages and disadvantages of using such models?

Zero-inflated models have been widely used in various fields, including epidemiology, economics, and environmental science, due to their ability to handle data with excessive zeros. However, like any statistical model, zero-inflated models have their own advantages and disadvantages. In this section, we will discuss some of the key benefits and limitations of using zero-inflated models for data analysis.

Advantages:

• Zero-inflated models allow for the modeling of datasets with excess zero values, which would not be possible with traditional models.
• They can provide more accurate predictions when dealing with datasets that contain a large proportion of zero values.
• They can be used to identify and differentiate between true zero values and zero values that are a result of excess zeros in the dataset.

Disadvantages:

• Zero-inflated models can be computationally intensive and require more time and resources to fit compared to traditional models.
• They require a larger sample size to obtain reliable parameter estimates.
• The interpretation of the results can be complex and may require expertise in statistical modeling.
• If the data is not truly zero-inflated, using a zero-inflated model can lead to overfitting and potentially biased results.

What are the applications of these models?

Zero-inflated models have several applications in different fields. Here are some examples:

1. Healthcare: In healthcare, zero-inflated models are used to study the frequency of hospitalizations and the number of emergency room visits. These models can help healthcare providers understand the factors that contribute to these outcomes, which can inform interventions to reduce hospitalizations and emergency room visits.
2. Ecology: In ecology, zero-inflated models are used to study the distribution of species in a particular ecosystem. By understanding the factors that contribute to the presence or absence of a particular species, researchers can develop strategies to protect endangered species and preserve ecosystems.
3. Economics: In economics, zero-inflated models are used to study the demand for goods and services. By understanding the factors that contribute to zero demand, businesses can develop strategies to increase demand and maximize profits.
4. Marketing: In marketing, zero-inflated models are used to study customer behavior. By understanding the factors that contribute to zero purchases, businesses can develop strategies to increase sales and improve customer retention.

Overall, zero-inflated models can be applied in any field where count data is collected and there is a high frequency of zero counts. These models can help researchers and practitioners understand the factors that contribute to these zero counts, which can inform strategies to improve outcomes.

How to fit a zero-inflated model in Python?

Fitting zero-inflated models can be done using several statistical software packages, including R, SAS, and Python. In Python, one popular package for fitting zero-inflated models is statsmodels. Here’s an example of how to fit a zero-inflated model using the ZeroInflatedPoisson class from statsmodels:

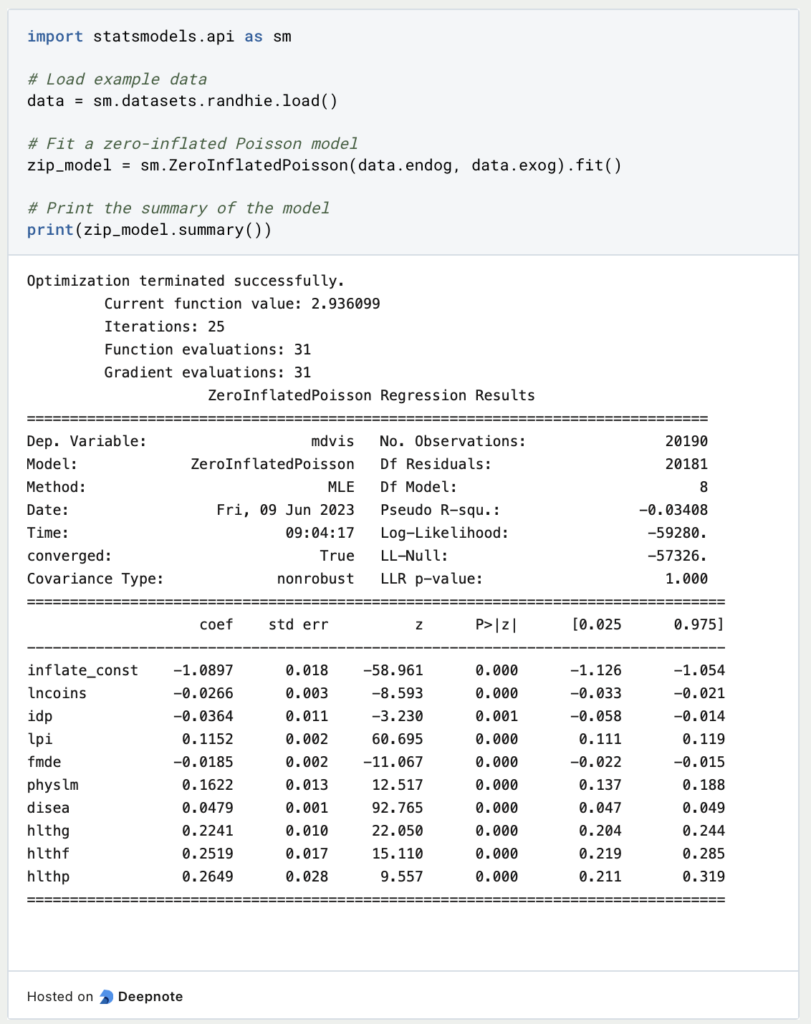
In this example, we loaded an example dataset from statsmodels and fitted a zero-inflated Poisson model using the ZeroInflatedPoisson class. The endog variable represents the response variable, and the exog variable represents the explanatory variables. After fitting the model, we printed a summary of the results using the summary() method. This summary includes information such as the coefficients, standard errors, and p-values for each variable in the model.

Note that there are several other classes available in statsmodels for fitting different types of zero-inflated models, including ZeroInflatedNegativeBinomial, ZeroInflatedBinomial, and ZeroInflatedGeneralizedPoisson. The syntax for fitting these models is similar to the example above, but the specific class and arguments will vary depending on the type of model you want to fit.

This is what you should take with you

• Zero-inflated models are a type of statistical model that can handle excessive zeros in count data
• They are useful in situations where there is an excess of zero counts compared to what would be expected by chance
• The two types of zero-inflated models are zero-inflated Poisson (ZIP) and zero-inflated negative binomial (ZINB)
• The advantages of zero-inflated models include their ability to handle over-dispersion and excessive zeros, while the disadvantages include the assumption that the zero inflation process is independent of the counting process
• Zero-inflated models have applications in many fields, such as epidemiology, ecology, and marketing
• Fitting a zero-inflated model involves identifying the appropriate model, estimating the parameters, and assessing the goodness of fit
• Python provides various packages such as statsmodels and Scikit-learn that can be used to fit zero-inflated models.

Other Articles on the Topic of Zero-Inflated Model

The University of Otago has an interesting script on this topic using a lot of examples. The slides can be found here.