Der Backpropagation Algorithmus ist ein Werkzeug zur Verbesserung des Neuronalen Netzwerkes während des Trainingsprozesses. Mit Hilfe dieses Algorithmus werden die Parameter der einzelnen Neuronen so abgeändert, dass die Vorhersage des Modells und der tatsächliche Wert möglichst schnell übereinstimmen. Dadurch kann ein Neuronales Netzwerk auch schon nach einer verhältnismäßig kurzen Trainingszeit gute Ergebnisse liefern.

Dieser Beitrag reiht sich in die anderen Beiträge zu Künstliche Intelligenz Grundlagen ein. Wenn Du noch keinen Background zum Thema Neural Networks und Gradientenverfahren hast, solltest Du bevor Du weiterliest, die verlinkten Beiträge anschauen. Wir werden auf diese Konzepte nur noch kurz eingehen können. Machine Learning im Allgemeinen ist ein sehr mathelastiges Themengebiet. Für diese Erläuterung von Backpropagation versuchen wir soweit wie möglich auf mathematische Herleitungen zu verzichten und lediglich ein Grundverständnis für die Vorgehensweise zu vermitteln.

Wie funktionieren Neuronale Netzwerke?

Neuronale Netze bestehen aus vielen Neuronen, die in verschiedenen Schichten organisiert sind und miteinander kommunizieren und verknüpft sind. In der Eingabeschicht werden den Neuronen verschiedene Inputs zur Berechnung gegeben. Das Netzwerk soll darauf trainiert werden, dass die Ausgabeschicht, die letzte Schicht, eine möglichst genaue Vorhersage auf Basis des Inputs macht, das dem tatsächlichen Ergebnis so nahe wie möglich kommt.

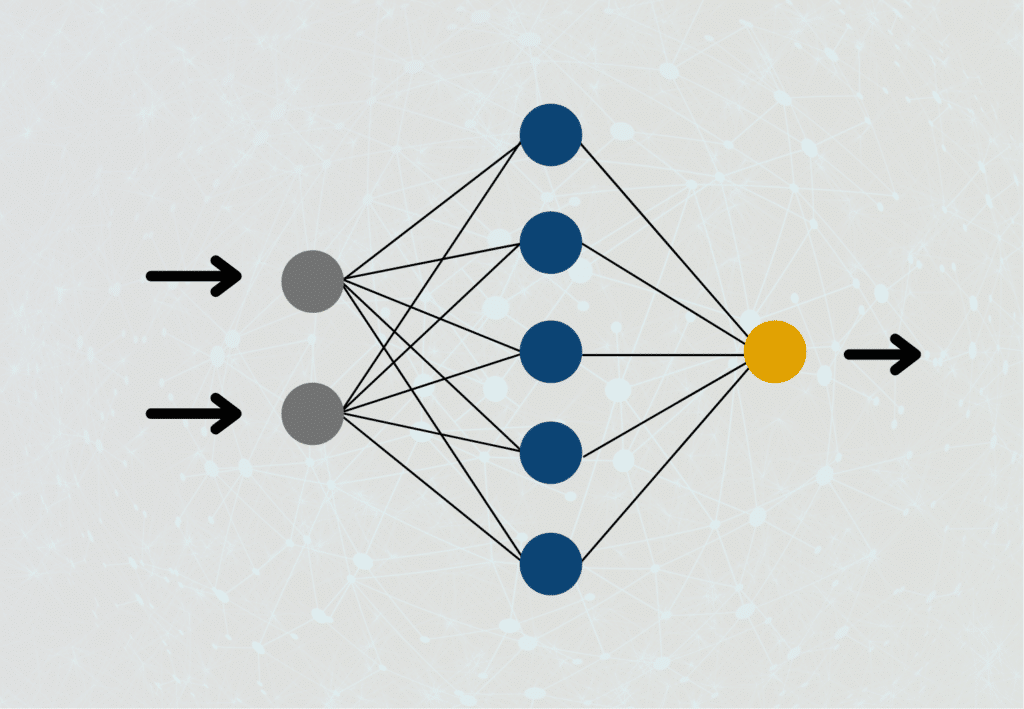
Dazu werden die sogenannten Hidden Layers genutzt. Diese Schichten enthalten auch viele Neuronen, die mit der vorherigen und der darauffolgenden Schicht kommunizieren. Während des Trainings werden die Gewichtungsparameter jedes Neurons so verändert, dass die Vorhersage sich der Realität so weit wie möglich annähert. Der Backpropagation Algorithmus hilft uns bei der Entscheidung, welchen Parameter wir wie abändern müssen, damit sich die Verlustfunktion minimiert.

Was ist das Gradientenverfahren?

Das Gradientenverfahren ist ein Algorithmus aus den mathematischen Optimierungsproblemen, der hilft, sich dem Minimum einer Funktion so schnell wie möglich zu nähern. Mathematisch berechnet man dazu die Ableitung einer Funktion, den sogenannten Gradienten, und geht in die entgegengesetzte Richtung dieses Vektors, weil dort der steilste Abstieg der Funktion ist.

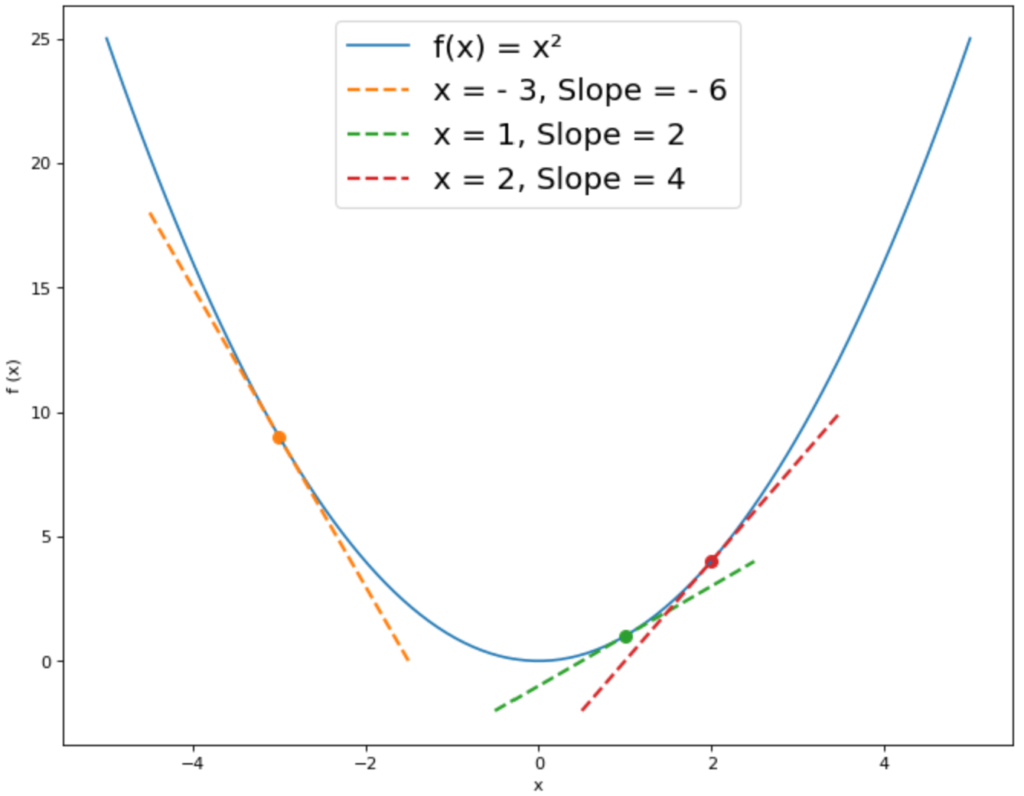
Wem das zu mathematisch ist, der kennt diese Vorgehensweise vielleicht vom Wandern in den Bergen. Man hat schweiß gebadet endlich den Gipfel erklommen, die obligatorischen Bilder gemacht und die Aussicht ausreichend genossen und möchte nun auf schnellstem Wege wieder ins Tal und zurück nach Hause. Man sucht also den schnellsten Weg vom Berg hinunter ins Tal, also das Minimum der Funktion. Intuitiv wird man dazu einfach den Weg gehen der für das Auge den steilsten Abstieg hat, weil man davon ausgeht, dass man so am schnellsten wieder bergab kommt. Das ist natürlich nur bildlich gesprochen, da sich keiner die steilste Klippe am Berg hinunter trauen wird.

Dasselbe macht das Gradientenverfahren mit der Funktion. Wir befinden uns irgendwo im Funktionsgraphen und versuchen das Minimum der Funktion zu finden. Entgegen dem Beispiel haben wir in dieser Situation nur zwei Möglichkeiten uns fortzubewegen. Entweder in die positive oder die negative x-Richtung (bei mehr als einer Variablen, also einem mehrdimensionalen Raum, sind es natürlich entsprechend mehr Richtungen). Der Gradient hilft uns dabei, indem wir wissen, dass die negative Richtung des Gradienten der steilste Funktionsabstieg ist.

Was ist das Gradientenverfahren im Machine Learning?

Die Funktion, welche uns beim Machine Learning interessiert, ist die Verlustfunktion. Sie misst den Unterschied zwischen der Vorhersage des Neuronalen Netzwerkes und dem tatsächlichen Ergebnis des Trainingsdatenpunktes. Auch diese Funktion wollen wir minimieren, da wir dann eine Differenz von 0 haben. Dann kann unser Modell exakt die Ergebnisse des Datensatzes vorhersagen. Die Stellschrauben um dort hinzukommen, sind die Gewichtungen der Neuronen, die wir ändern können, um dem Ziel näher zu kommen.

In Kurzform: Während des Trainings erhalten wir die Verlustfunktion, deren Minimum wir versuchen zu finden. Dazu berechnen wir nach jeder Wiederholung den Gradienten der Funktion und gehen in die Richtung des steilsten Abstiegs der Funktion. Leider wissen wir nun noch nicht, welchen Parameter wir wie stark abändern müssen, um die Verlustfunktion zu minimieren. Das Problem dabei ist, dass das Gradientenverfahren immer nur für die vorhergegangene Layer und deren Parameter durchgeführt werden kann. Ein tiefes Neuronales Netzwerk besteht jedoch aus vielen verschiedenen Hidden Layern, deren Parameter theoretisch alle für den Fehler verantwortlich sein können.

In großen Netzwerken müssen wir also auch feststellen, wie groß der Einfluss der einzelnen Parameter auf den schlussendlichen Fehler waren und wie stark wir sie abändern müssen. Das ist die zweite Säule der Backpropagation in Deep Learning, woher auch der Name kommt.

Wie funktioniert der Backpropagation Algorithmus?

Wir versuchen diesen Beitrag so unmathematisch wie möglich zu halten, aber ganz ohne geht es leider nicht. Jede Schicht in unserem Netzwerk ist definiert durch einen Input, entweder aus der vorangegangenen Layer oder aus dem Trainingsdatensatz, und über einen Output, der an die nächsten Schicht weitergegeben wird. Der Unterschied zwischen Input und Output entsteht durch die Gewichtungen und die Aktivierungsfunktionen der Neuronen.

Das Problematische daran ist, dass der Einfluss den eine Schicht auf den schlussendlichen Fehler hat auch davon abhängig ist, wie die nachfolgende Schicht diesen Fehler weitergibt. Selbst wenn sich ein Neuron “verrechnet” fällt das nicht so stark ins Gewicht, wenn das Neuron in der nächsten Schicht diesen Input einfach ignoriert, also dessen Gewichtung auf 0 setzt. Dies zeigt sich mathematisch daran, dass der Gradient einer Schicht auch die Parameter der nachfolgenden Schicht enthält. Deshalb müssen wir die Backpropagation in der letzten Schicht, der Ausgabeschicht, beginnen und dann Schicht für Schicht mit dem Gradientenverfahren die Parameter optimieren.

Von daher kommt auch der Name Backpropagation, oder auch Fehlerrückführung, da wir den Fehler von hinten durch das Netzwerk propagieren und die Parameter optimieren.

Wie funktioniert der Vorwärts- und Rückwärtsdurchlauf im Detail?

Der sogenannte Vorwärtsdurchlauf beschreibt den normalen Prozess einer Vorhersage in einem neuronalen Netz von der Eingabeschicht über die Hidden Layers zur Ausgabeschicht. Während dieses Durchlaufs werden die Inputs in jeder Schicht mithilfe einer linearen Transformation verändert und anschließend mithilfe der Aktivierungsfunktion in einen vordefinierten Zahlenbereich skaliert. Wenn die Ausgabe schließlich erreicht ist, werden die Werte der letzten Schicht mit dem Zielwert aus dem Datensatz verglichen und die Abweichung, also den Verlust oder Fehler, berechnet.

Beim Rückwartsdurchlauf, oder englisch Backward Pass, ist dieser Prozess etwas komplexer. Das Ziel ist es hierbei, die Gewichte der einzelnen Neuronen so anzupassen, dass der Fehler minimiert wird und dadurch die Genauigkeit der Modellvorhersagen weiter erhöht wird.

Um die Höhe und die Richtung der Anpassung bestimmen zu können, kommt der Gradient der Verlustfunktion ins Spiel. Dieser wird mithilfe der mathematischen Kettenregel berechnet und enthält die Ableitung des Fehlers nach jeder einzelnen Gewichtsvariablen der Neuronen. Dazu wird zuerst die partielle Ableitung des Verlusts in Bezug auf die Ausgabe jedes einzelnen Neurons berechnet. Anschließend wird diese Ableitung wiederum partiell in Bezug auf jedes Gewicht abgeleitet.

Nachdem dieser Gradient des neuronalen Netzes berechnet oder mithilfe von Optimierungsalgorithmen, wie beispielsweise dem stochastischen Gradientenabstieg, angenähert wurde, können die Gewichte des neuronalen Netzes aktualisiert werden. Sie werden so angepasst, dass die Verlustfunktion weiter minimiert wird und die Leistung des Netzes damit verbessert wird.

Die Schlüsselkomponenten in diesem Prozess sind die Kettenregel und Näherungsmethoden für den Gradienten, sodass schnelle Berechnungen auch mit großen Datensätzen und einem weit verflechteten Netz möglich sind. Dadurch lassen sich wiederum mehr Trainingsdurchläufe in derselben Zeit absolvieren, wodurch wiederum die Genauigkeit des Modells zunehmen kann.

Nichtsdestotrotz ist die Backpropagation sehr rechenintensiv, weshalb weitere Optimierungstechniken und Modifikationen erfunden wurden, die die Komplexität der Berechnungen reduzieren sollen und somit den Ablauf beschleunigen. Dazu gehören beispielsweise das Training in Mini-Batches oder adaptive Lernraten.

Welche Vorteile bringt der Backpropagation Algorithmus?

Dieser Algorithmus bietet einige Vorteile beim Training von Neuronalen Netzwerken. Dazu gehören unter anderem:

• Einfache Nutzung: Die Fehlerrückführung kann einfach und schnell umgesetzt werden und in das Netzwerk Training eingebaut werden.
• Keine zusätzlichen Hyperparameter: Im Gegensatz zu Neuronalen Netzwerken werden bei der Backpropagation keine zusätzlichen Hyperparameter eingeführt, die die Leistung des Algorithmus beeinflussen.
• Standardmethode: Die Anwendung der Fehlerrückführung ist mittlerweile zum Standard geworden und wird deshalb bereits standardmäßig in vielen Modulen ohne zusätzliche Programmierung angeboten.

Wie verhält sich die Backpropagation im Vergleich zu anderen Modellen?

Die Backpropagation ist der zentrale Lernalgorithmus hinter neuronalen Netzwerken im Bereich des Supervised Learnings. Jedoch gibt es abhängig von der Modellarchitektur auch andere Algorithmen, die das Erlernen von Strukturen aus Daten ermöglichen.

In dieser Sektion wollen wir die Backpropagation mit anderen, gängigen Lernalgorithmen aus dem Bereich des Supervised Learnings vergleichen:

• Decision Trees: Entscheidungsbäume werden im Bereich des Supervised Learnings sowohl für Regression- als auch für Klassifizierungsaufgaben genutzt. Dabei wird der Baum aufgebaut, indem iterativ versucht wird, eine möglichst gute Aufteilung des Datensatzes in Teilmengen anhand eines bestimmten Merkmals vorzunehmen. Dabei können sowohl kategorische als auch kontinuierliche Daten verarbeitet werden. Jedoch sind die Decision Trees anfällig für das sogenannte Overfitting und können bei komplexen Datensätzen zu unbefriedigenden Ergebnissen führen.
• Support Vector Machine (SVMs): Support Vector Machines stammen aus dem Bereich des Supervised Learnings und können auch für Klassifikationen oder Regressionen verwendet werden. Dabei wird eine sogenannte Hyperebene gesucht, welche den Abstand zwischen zwei Datenklassen maximiert. Das Finden einer solchen Ebene kann sehr rechenintensiv werden und erfordert eine gute Anpassung der Hyperparamter. Außerdem funktionieren SVMs meist am besten für lineare Daten, obwohl sie auch für nicht-lineare Daten genutzt werden können.
• k-nearest neighbor (k-NN): Der k-NN Algorithmus findet die k-nächstgelegenen Datenpunkt zu einer Eingabe und versucht anhand dieser Punkte eine gute Vorhersage zu treffen. Die Leistungsfähigkeit dieses Modells hängt von der Wahl der Abstandsmetrik ab und kann sowohl mit kategorialen als auch mit kontinuierlichen Daten umgehen. Außerdem können mithilfe von k-NN Regressionen und Klassifizierungen umgesetzt werden. Bei hochdimensionalen Daten kann dieser Algorithmus die Leistungsfähigkeit verlieren, da dann die Abstandsberechnung nicht nur komplex wird, sondern auch ungenau werden kann.

Im Vergleich zu diesen Algorithmen hat die Backpropagation einige einzigartige Merkmale und Vorteile:

1. Die Backpropagation kann im Vergleich zu den anderen Lernalgorithmen besonders gut mit großen Datenmengen und hochdimensionalen Daten umgehen. Außerdem lassen sich im neuronalen Netz auch komplexe Zusammenhänge zwischen Inputs und Outputs abbilden, die mit den anderen Modellen möglicherweise nicht möglich wären.
2. Die Backpropagation erweist sich als durchaus flexibel, da sie sowohl mit kontinuierlichen als auch mit kategorialen Daten umgehen kann, wie dies die anderen Lernalgorithmen auch konnten. Dadurch bietet sich die Backpropagation für verschiedenste Anwendungen an.
3. Durch die Wahl der Aktivierungsfunktion lassen sich auch nichtlineare Beziehungen zwischen den Input- und den Outputvariablen abbilden.
4. Mithilfe der Backpropagation lassen sich auch hierarchische Darstellungen von Daten erlernen, wie sie beispielsweise in Bildern oder in natürlicher Sprache vorkommen.
5. Jedoch hat auch die Backpropagation, genau wie die anderen Lernalgorithmen, Probleme mit Overfitting, also generalisiert nicht immer ausreichend, um auch gute Ergebnisse auf neuen Daten zu liefern. Weitere Probleme ergeben sich mit den sogenannten verschwindenden Gradienten, also Gradienten, die so klein sind, dass keine oder nur kleine Änderungen an den Neuronengewichten vorgenommen werden, wodurch das Modell nicht mehr ausreichend lernt. Um diesen Problemen entgegenzuwirken, wurden verschiedene Optimierungstechniken vorgeschlagen, wie beispielsweise die Regularisierung oder die Einführung von sogenannten Dropoutschichten in der Netzwerk-Architektur.

Die Backpropagation in neuronalen Netzwerken ist ein mächtiger Lernalgorithmus im Bereich des Supervised Learnings. Wenn genügend Rechenleistung vorhanden ist, kann dieser in vielen Fällen anderen Lernalgorithmen vorgezogen werden, da sich damit sehr komplexe Zusammenhänge erlernen lassen.

Außerdem bietet die Backpropagation Vorteile bei großen und hochdimensionalen Datensätzen mit denen die anderen Lernalgorithmen hingegen Probleme hatten.

Das solltest Du mitnehmen

• Backpropagation ist ein Algorithmus zum Training von Neuronalen Netzwerken.
• Er ist unter anderem die Anwendung des Gradientenverfahrens auf die Verlustfunktion des Netzwerkes.
• Der Name kommt daher, dass der Fehler vom Ende des Modells Schicht für Schicht nach vorne propagiert wird.

Andere Beiträge zum Thema Backpropagation

• Tensorflow bietet eine ausführliche Erklärung zu Gradienten und Backpropagation und zeigt auch direkt, wie sich das Ganze in Python umsetzen lässt.