Damit Machine Learning Modelle lernen und ihre Vorhersagen verbessern können, benötigen sie sogenannte Verlustfunktionen, die messen, wie groß die Differenz zwischen der Vorhersage und dem tatsächlichen Wert ist. Die Binary Cross-Entropy (BCE) ist eine zentrale Verlustfunktion, die für binäre Klassifikationen genutzt wird, also solche, die Objekte einer von zwei Klassen zuordnen. Egal ob bei der Erkennung von Spam-Mails oder bei der medizinischen Diagnose von Patienten, die Binary Cross-Entropy hilft, Modelle präzise und zuverlässig zu trainieren. 

In diesem Beitrag beschäftigen wir uns grundsätzlich damit, was Verlustfunktionen sind und wie die Binary Cross-Entropy funktioniert. Dazu schauen wir uns auch im Detail den mathematischen Aufbau der Funktion an und erklären diesen anhand eines einfachen Beispiels. Außerdem sprechen wir über die vielfältigen Anwendungsbereiche, in denen BCE eingesetzt wird, und beleuchten die Vor- und Nachteile dieser Verlustfunktion.

Was ist eine Verlustfunktion?

Die Verlustfunktion, auch Zielfunktion oder Kostenfunktion genannt, beschreibt ein entscheidendes Konzept im Machine Learning, das die Leistung des trainierenden Modells bewertet und den Lernprozess steuert. Einfach gesagt berechnet sie den Unterschied zwischen den tatsächlichen Zielwerten im Datensatz und den Vorhersagen des Modells. Damit misst sie kurz gesagt, wie gut oder schlecht das Modell performt. 

Während des Trainingsprozesses dient die Verlustfunktion als Richtlinie, um die Modellparameter, wie zum Beispiel die Neuronengewichtungen in einem neuronalen Netzwerk, zu optimieren. Dabei werden allgemein die folgenden Schritte durchlaufen: 

1. Die Verlustfunktion berechnet den aktuellen Fehler des Modells. 
2. Die Modellparameter werden so abgeändert, dass sie den Fehler im nächsten Trainingslauf deutlich reduzieren. Dazu kann beispielsweise die sogenannte Backpropagation genutzt werden.  
3. Dieser Vorgang wird so lange wiederholt, bis das Modell einen möglichst geringen Fehler erreicht hat und im besten Fall im globalen Minimum der Verlustfunktion angekommen ist. 

Ohne die Verlustfunktion wäre es nicht möglich, ein Modell zu trainieren, da eine Methode fehlen würde, um die Qualität der Vorhersagen zu bewerten. Mithilfe dieser Funktion gibt es jedoch konkrete mathematische Berechnungen, die vorgenommen werden können, um die Modellparameter zu verändern und das Modell zu verbessern. Eine gute Verlustfunktion sollte die folgenden Eigenschaften besitzen: 

1. Sie sollte sensibel gegenüber Abweichungen der Vorhersagen sein, sodass auch kleine Diskrepanzen zwischen Vorhersage und Zielwert ins Gewicht fallen und erkannt werden können. 
2. Abhängig vom Modell sollte die Verlustfunktion außerdem differenzierbar sein, es sollte also die Ableitung der Funktion definiert sein. Dadurch können Methoden, wie zum Beispiel der Gradientenabstieg genutzt werden, welcher Differenzierungen nutzt. 
3. Die Funktion sollte auf die Merkmale des spezifischen Modells angepasst werden, sodass damit beispielsweise Klassifikationen abgebildet werden können. 

In Kombination mit dem passenden Modell ist die Verlustfunktion ein zentrales Werkzeug, um leistungsstarke und genaue Machine Learning Modelle zu trainieren, die in diversesten Anwendungen genutzt werden können. 

Was ist die Binary Cross-Entropy?

Die Binary Cross–Entropy Loss ist eine Verlustfunktion, die für binäre Anwendungen genutzt wird, also wenn die Vorhersagen nur einen von zwei Zuständen annehmen kann, zum Beispiel „wahr/falsch“ oder „krank/gesund“. Dies wird beispielsweise in Klassifikationen genutzt, bei denen die Kreditwürdigkeit von Personen in „gut“ und „schlecht“ klassifiziert werden sollen. Innerhalb des Machine Learnings ist sie eine der wichtigsten Verlustfunktionen und wird in vielen binären Klassifikationen verwendet.

Mithilfe der Binary Cross-Entropy kann gemessen werden, wie nahe die Vorhersage des Modells beim tatsächlichen Zielwert liegt. Dazu werden die Klassifikationen des Modells so konstruiert, dass sie zwischen 0 und 1 liegen, wobei 0 die Zugehörigkeit zu der einen Klasse anzeigt, wie zum Beispiel „falsch“ oder „krank“, und 1 die Zugehörigkeit zur anderen Klasse, wie „wahr“ oder „gesund”. Das Modell kann hierbei alle Werte zwischen 0 und 1 vorhersagen, wobei der Abstand zu den jeweiligen Klassen Auskunft darüber gibt, wie sicher sich das Modell ist, dass ein Datenpunkt einer Klasse zugeordnet werden soll.

Ein Wert von 0,15 beispielsweise deutet darauf hin, dass sich das Modell ziemlich sicher ist, dass der Datenpunkt der Klasse 0 zugeordnet werden soll, während eine Vorhersage von 0,48 dafürspricht, dass sich das Modell nicht wirklich entscheiden kann. Die Stärke der Binary Cross-Entropy liegt darin, dass sie falsche Vorhersagen mit einer hohen Sicherheit stärker bestraft und damit das Modell dazu führt, richtige Entscheidungen mit hoher Sicherheit zu treffen. 

Die mathematische Formulierung der Binary Cross-Entropy lautet: 

\(\)\[\text{BCE} = -\frac{1}{N} \sum_{i=1}^{N} \left[ y_i \cdot \log(\hat{y}_i) + (1 – y_i) \cdot \log(1 – \hat{y}_i) \right]\]

Dabei ist \(y_i\) die tatsächliche Klasse des Datenpunktes und \(\hat{y_i}\) ist die vorhergesagte Klasse des Modells für diesen Datenpunkt. Die Anzahl der Datenpunkte im Datensatz wird durch \(N\) repräsentiert. Die Fehler aller Datenpunkte wird schließlich aufsummiert und dann durch die Anzahl der Datenpunkte geteilt, um einen Mittelwert zu errechnen. 

Darüber hinaus besteht die Binary Cross-Entropy aus den folgenden zwei Bestandteilen: 

1. \(y_i \cdot \log(\hat{y_i})\): Dieser Termin bewertet den Verlust, wenn die tatsächliche Klasse \(y_i = 1\) ist. Der Verlust in diesem Teil wird minimiert, wenn die Vorhersage \(\hat{y_i}\) nahe bei 1 liegt. Der zweite Teil der Verlustfunktion fällt automatisch heraus, da \(1 – y_i = 0\) und somit keinen Einfluss besitzt. 
2. \((1-y_i) \cdot \log(1-\hat{y_i})\): Dieser zweite Teil der Funktion wird aktiviert, wenn die tatsächliche Klasse 0 ist, also \(y_i = 0\). Der erste Teil der Gleichung fällt raus, da der Logarithmus mit \(y_i\), also 0, multipliziert wird. Hierbei wird der Verlust minimiert, wenn sich das Modell besonders sicher ist und die Vorhersage \(\hat{y_i}\) nahe bei 0 liegt. 

Der Binary Cross–Entropy Loss zeichnet sich dadurch aus, dass Fehler asymmetrisch behandelt werden, sodass größere Fehler und Abweichungen stärker bestraft werden als kleinere Abweichungen. Das mag im ersten Moment als unlogisch erscheinen, da eigentlich alle Fehler in einer binären Klassifikation erstmal „gleich schlecht“ sind, da die falsche Klasse vorhergesagt wurde. In der Praxis ist es jedoch auch wichtig, wie sicher sich das Modell bei einer Klassifizierung ist, um unterschiedliche Vorhersagen in ähnlichen Fällen zu verhindern, die die Glaubwürdigkeit des Modells gefährden könnten. 

Was sind die theoretischen Konzepte der Binary Cross-Entropy?

Wie der Name Binary Cross-Entropy schon verrät, enthält diese Verlustfunktion einige theoretische Konzepte aus der Informationstheorie und der Statistik, die essenziell sind, um die Funktionalität dieser Loss Function genauer zu verstehen. 

Die BCE wird bei Modellen verwendet, die eine binäre Klassifikation vorhersagen und dafür Wahrscheinlichkeiten benutzen. Diese befinden sich in einem Bereich zwischen 0 und 1, wobei eine Wahrscheinlichkeit nahe 1 bedeutet, dass sich das Modell sehr sicher ist, dass ein Datenpunkt der Klasse 1 zugeordnet werden sollte und ein Wert nahe 0 entsprechend bedeutet, dass das Modell dem Datenpunkt die Klasse 0 zuordnen würde. 

Logarithmus

Die logarithmischen Terme \(\log(\hat{y_i})\) und \(\log(1-\hat{y_i})\) dienen dazu,  die Vorhersagen des Modells nicht linear zu bewerten, sondern das Modell dafür zu belohnen, wenn es sich bei den Entscheidungen sicher ist. 

Der Logarithmus zeichnet sich durch sein exponentielles Wachstum aus, welches dafür sorgt, dass Werte nahe Null absolut einen sehr großen Wert annehmen und für Werte nahe 1 absolut einen sehr kleinen Wert annehmen. Dadurch sorgt die Verlustfunktion für eine starke Belohnung für Entscheidungen, die mit einer hohen Wahrscheinlichkeit getroffen wurden, wobei erstmal irrelevant ist, ob diese korrekt waren oder nicht. 

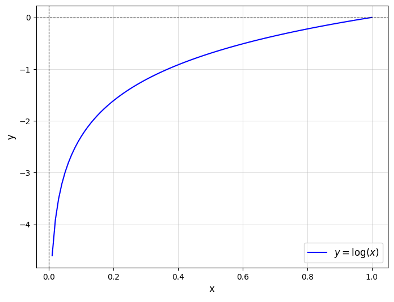
Die Binary Cross-Entropy bezieht die Korrektheit der Vorhersage mit ein, indem sie die zwei Terme innerhalb der Klammern besitzt. Wenn der Datenpunkt tatsächlich der Klasse 0 angehört, dann bestimmt nur der zweite Teil des Terms über den Verlust. Wenn das Modell hier fälschlicherweise einen Wert nahe 1 vorhersagt, dann nähert sich der Term innerhalb des Logarithmus der Null an und das Modell wird stärker bestraft, als wenn es sich unsicher ist, also einen Wert von 0,5 vorhersagt oder sogar eine korrekte Vorhersage nahe der 1 trifft. 

Der Logarithmus ist außerdem für das Minus am Anfang des Terms verantwortlich. Wie im Diagramm deutlich wird, ist der Logarithmus im Bereich zwischen 0 und 1 im negativen y-Bereich. Somit ist die Summe innerhalb der Klammern auch negativ, da weder \(y_i\) noch \(1-y_i\) per Definition negativ werden können und somit die beiden Produkte auch immer negativ bleiben werden. Da Verlustfunktionen üblicherweise positiv sind, nutzt man das vorangestellte Minus, um sicherzustellen, dass der gesamte Term positiv wird. 

Entropie und Kreuzentropie

Die Entropie beschreibt ein Konzept aus der Informationstheorie, welches misst, wie unsicher oder unvorhersehbar eine Situation oder ein Ereignis ist. Wenn ein Ereignis sehr sicher und vorhersehbar ist, ist wenig Entropie vorhanden, wie zum Beispiel bei einem Münzwurf, bei dem es in der Praxis nur zwei mögliche Ergebnisse gibt: Kopf oder Zahl (wenn man ausschließt, dass die Münze auf dem Rand landet). Wenn ein Ereignis hingegen schwer vorherzusagen ist, dann besitzt es eine hohe Entropie, da es unsicherer ist. Im Vergleich zum Münzwurf besitzt das Würfeln eines Würfels eine höhere Entropie, da es schwieriger ist, dieses Ereignis vorherzusagen. 

Die Kreuzentropie geht darüber hinaus und vergleicht zwei Wahrscheinlichkeitsverteilungen, genauer gesagt: 

• Die wahre Verteilung, die dem Zufallsereignis zugrunde liegt und die tatsächlichen Ergebnisse oder Zielwerte aus dem Datensatz umfasst. 
• Die vorhergesagte Verteilung, welche die Wahrscheinlichkeitsverteilung beschreibt, die vom Modell im Laufe des Trainings erlernt wird. 

Im besten Fall nähert sich das Modell im Lauf der Zeit an die wahre Verteilung an. Die Kreuzentropie hilft dabei genau diese Eigenschaft zu messen. In einer perfekten Welt würde ein gutes Modell eine Wahrscheinlichkeit von 1 vorhersagen, wenn ein Datenpunkt der Klasse 1 angehört und vice versa. In der Realität ist dies jedoch nur selten der Fall und die vorhergesagten Wahrscheinlichkeiten nähern sich vielmehr diesen Extremwerten an. 

Die Binary Cross-Entropy implementiert die Kreuzentropie, indem es das Modell besonders hart bestraft, wenn das Modell eine besonders hohe Wahrscheinlichkeit für ein falsches Ergebnis vorhersagt, denn das ist die Differenz zwischen wahrer Verteilung und vorhergesagter Verteilung hoch. Dieses Verhalten wird mithilfe der beschriebenen Eigenschaften des Logarithmus und dem Term, der beide Zustände umfasst, mathematisch implementiert. 

Welche Anwendungen nutzen Binary Cross Entropy?

Die Binary Cross-Entropy ist eine zentrale Verlustfunktion im Bereich des Machine Learnings und wird in den verschiedensten Anwendungen eingesetzt. Aufgrund ihres Aufbaus ist sie vor allem für binäre Klassifikationen, wie die folgenden, gut geeignet: 

• Spam-Erkennung: BCE wird verwendet, um betrügerische Aktivitäten festzustellen und entsprechende Objekte zu klassifizieren. Dabei kann es zum Beispiel bei der Erkennung von Spam-Emails genutzt werden oder bei betrügerischen Überweisungen von Bankkonten. 
• Krankheitsdiagnose: Innerhalb des Gesundheitswesens kann die BCE-Verlustfunktion für Modelle verwendet werden, die bei medizinischen Diagnosen unterstützen. Diese können so trainiert werden, dass sie anhand von verschiedenen Symptomen und Messwerten eines Patienten eine Vorhersage treffen, ob dieser an einer bestimmten Krankheit leidet oder nicht. 
• Sentimentanalyse: Das Natural Language Processing beschäftigt sich damit, menschliche Sprache für Maschinen verständlich zu machen und somit Texte verarbeiten zu können. Die Sentimentanalyse versucht eine Vorhersage zu treffen, ob eine Passage eine positive oder negative Stimmung wiedergibt. Das kann vor allem für Social Media Kommentare oder Produktbewertungen genutzt werden, um hier eine schnelle Einordnung zu erhalten und diese Kommentare dann gesondert zu bearbeiten. 

Dies sind nur einige wenige der Anwendungen, in denen die Binary Cross-Entropy eingesetzt wird. Aufgrund ihrer positiven Eigenschaften hat sie sich als Standardverlustfunktion für verschiedenste Modellarchitekturen etabliert. 

Was sind die Vor- und Nachteile von BCE?

Die Nutzung der Binary Cross-Entropy bietet unterschiedlichste Vorteile für die Nutzung im Bereich des Machine Learnings. Jedoch gibt es auch einige Herausforderungen und Probleme, die bei der Anwendung berücksichtigt werden müssen. Deshalb arbeiten wir in diesem Abschnitt die Chancen und Herausforderungen auf, damit abhängig von der Anwendung eine fundierte Entscheidung getroffen werden kann, ob die Binary Cross-Entropy die richtige Verlustfunktion ist. 

Vorteile:

• Spezialisierung auf binäre Klassifikationen: Die Architektur dieser Verlustfunktion ist für Anwendungen mit zwei Klassen ausgelegt und funktioniert für diese sehr gut. Außerdem ist sie in diesem Kontext meist leicht anzuwenden, da die Modelle für eine Nutzung mit BCE ausgelegt sind. 
• Intuitive Modellbewertung: Die Interpretation der Ergebnisse ist besonders einfach, da niedrigere Werte auf ein besseres Modell hindeuten. Ein hoher Wert hingegen, deutet darauf hin, dass die vorhergesagte Klasse meist nicht mit der tatsächlichen übereinstimmt oder sich das Modell nicht sehr sicher bei der Vorhersage ist. 
• Vergleichbarkeit von Modellen: BCE kann zusätzlich zum Vergleich von verschiedenen Modellarchitekturen verwendet werden, die auf demselben Datensatz trainiert wurden. Aufgrund der festen mathematischen Grundlage ist die Architektur am besten, welche den niedrigsten Verlustwert auf Basis der BCE liefert. Dadurch können einfach verschiedene Architekturen getestet werden und anschließend das Modell gewählt werden, welches die besten Ergebnisse für diesen Datensatz liefert. 
• Sensibilität für Wahrscheinlichkeiten: Im Vergleich zu anderen Verlustfunktionen, legt BCE nicht nur Wert darauf, dass das Modell die richtigen Vorhersagen trifft und dadurch eine hohe Genauigkeit erzielt, sondern belohnt auch Modelle, die dies mit einer hohen Wahrscheinlichkeit, also einer hohen Sicherheit, tun. 
• Kombination mit Aktivierungsfunktionen: Vor allem im Bereich der neuronalen Netzwerke lässt sich BCE zusätzlich mit verschiedenen Aktivierungsfunktionen, wie zum Beispiel der Softmax-Funktion, kombinieren. 

Nachteile: 

• Probleme bei unausgeglichenen Datensätzen: Ein häufiges Problem in der Erstellung eines Klassifizierungsmodell ist der unausgewogene Datensatz, der häufig mehr Beispiele für eine als für die andere Klasse enthält. In der Medizin beispielsweise enthalten viele Datensätze mehr gesunde als erkrankte Patienten, da diese einfach häufiger vorkommen. In solchen Fällen kann es auch mit BCE zu unausgewogenen Ergebnissen kommen, da die häufigere Klasse dominiert und das Modell dazu neigt die seltenere Klasse schlichtweg zu ignorieren. Um diesem Problem entgegenzusteuern, kann eine gewichtete Binary Cross-Entropy genutzt werden, welche der unterrepräsentierten Klasse eine höhere Gewichtung zuweist und dem genannten Verhalten somit entgegensteuert. 
• Numerische Stabilität: In den Extremfällen, in denen sich das Modell besonders sicher ist und entweder \(\hat{y_i} = 0\) oder \(\hat{y_i} = 1\) vorhersagt, passiert es, dass der Verlustwert gegen undendlich strebt, da \(log(0) \rightarrow – \infty\). Obwohl dieses Szenario nur sehr selten vorkommt, kann es eintreten und zu numerischen Problemen führen. Um dies zu verhindern, können die Vorhersagen zu begrenzt werden, dass sie zwar Werte sehr nahe bei 0 und 1 annehmen können, aber eben nicht exakt diese Werte, zum Beispiel: \(\hat{y_i} = max(\epsilon, 1-\epsilon)\). 
• Interpretation bei Wahrscheinlichkeiten: Die Binary Cross-Entropy ist eine Verlustfunktion, welche die Differenz zwischen den vorhergesagten Wahrscheinlichkeiten und den tatsächlichen Klassen misst. Die schlussendliche Klassifizierung des Modells hängt dabei jedoch nicht nur von der Vorhersage ab, sondern auch vom gewählten Schwellenwert, der zur Unterscheidung der Klassen gewählt wird. Im einfachsten Fall kann die 0,5 als Schwellenwert genutzt werden, sodass jede Vorhersage größer 0,5 eine Zuordnung zur Klasse 1 bedeutet. In der medizinischen Diagnose und anderen Anwendungen können jedoch auch andere Schwellenwerte genutzt werden, die einen großen Einfluss auf die Genauigkeit des Modells haben.

Die Binary Cross-Entropy ist eine mächtige Verlustfunktion, die große Vorteile besitzt bei der Nutzung mit binären Klassifikationsmodellen. Jedoch kann es auch zu Problemen kommen, wenn der Datensatz unausgewogen ist. Die genannten Punkte sollten deshalb beachtet werden, bevor man die Binary Cross-Entropy für das eigene Modell nutzt. 

Wie kann die Binary Cross-Entropy mit mehr als zwei Klassen verwendet werden?

Obwohl die Binary Cross-Entropy für Klassifizierungsmodelle mit lediglich zwei Klassen konzipiert ist, kann sie mit leichten Änderungen auch für Mehrklassenprobleme verwendet werden. Der gängigste Ansatz dafür ist der sogenannte „One-vs-all“ oder „One-vs-rest“, der die Klassenbezeichnungen in einem binären Format organisiert, sodass ein Modell trainiert werden kann, welches binäre Vorhersagen trifft. 

Eine Anwendung mit drei Klassen „A“, „B“ und „C“ kann dann beispielsweise so umgeschrieben werden, dass sich daraus binäre Vektoren mit drei Einträgen ergeben. Somit hat ein Datenpunkt, welcher Klasse „B“ angehört, nicht als Zielwert „B“, sondern [0, 1, 0]. Das Modell, wie beispielsweise ein neuronales Netzwerk, müsste dann so abgeändert werden, dass die Ausgabeschicht drei Knoten hat und an jedem Knoten eine Wahrscheinlichkeit zwischen 0 und 1 vorhersagt. 

Dadurch kann die Binary Cross-Entropy für jede Klasse einzeln berechnet werden, da es sich dabei um eine isolierte, binäre Klassifizierung handelt, und anschließend der Gesamtverlust aus der Summe über die einzelnen Klassen berechnet werden. 

Wie kann man die Binary Cross-Entropy in Python nutzen?

Die Binary Cross-Entropy ist Teil von vielen Modulen in Python, wie zum Beispiel PyTorch oder TensorFlow, und kann in diesen Bibliotheken sehr einfach in bestehende Modelle integriert werden. In diesem Abschnitt schauen wir uns ein einfaches Beispiel an, wie man die Binary Cross-Entropy aus TensorFlow laden und nutzen kann. 

Dazu laden wir TensorFlow und erstellen zwei einfache Listen, eine davon mit fiktiven Klassenzuordnungen von drei Datenpunkten und eine mit den hypothetischen Vorhersagen, die ein Modell dazu gemacht hat. 

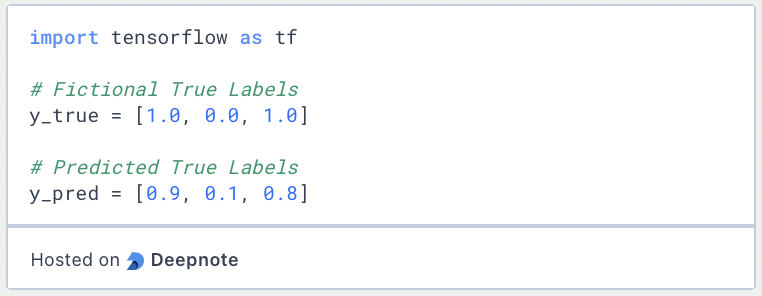
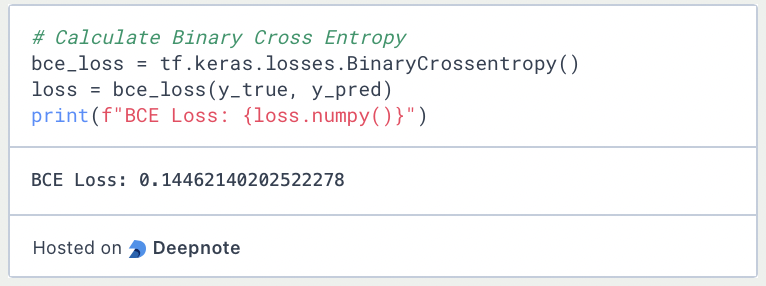
Anschließend können wir die Funktion BinaryCrosentropy() aus den Verlustfunktionen von Keras laden und die beiden Listen als Parameter übergeben. Damit erhalten wir dann den Verlustwert für den Datensatz bestehend aus drei Datenpunkten.

Das solltest Du mitnehmen

• Die Binary Cross-Entropy ist eine zentrale Verlustfunktion im Machine Learning, die für binäre Klassifikationsmodelle genutzt wird.
• Sie zeichnet sich dadurch aus, dass sie nicht nur die Genauigkeit eines Modells in den Verlust einbezieht, sondern auch die Sicherheit mit der ein Modell die richtige Klasse vorhersagt.
• Durch den Logarithmus werden größere Abweichungen von der richtigen Klasse auch stärker bestraft als kleine Abweichungen.
• Die Nutzung der Binary Cross-Entropy kann zu Problemen führen, wenn der Datensatz unausgewogen ist oder das Modell die Extremwerte 0 oder 1 vorhersagt.
• Die Binary Cross-Entropy kann mithilfe des “One-vs-all” Ansatz auch für Mehrklassenprobleme verwendet werden.
• In Python bieten verschiedene Bibliotheken, wie PyTorch oder TensorFlow, Funktionen mit denen die Binary Cross-Entropy einfach verwendet werden kann.

Andere Beiträge zum Thema Binary Cross Entropy

Hier findest Du die TensorFlow-Dokumentation, die erklärt, wie man die Verlustfunktion verwendet.