Der Softmax ist eine mathematische Funktion, die vor allem im Bereich des Machine Learnings dafür genutzt wird, einen Vektor mit Zahlen in einen Vektor mit Wahrscheinlichkeiten umzuwandeln. Vor allem in Neuronalen Netzwerken dient sie als sogenannte Aktivierungsfunktion der einzelnen Schichten.

Was ist eine Aktivierungsfunktion?

Die Aktivierungsfunktion kommt in den Neuronen eines Neuronalen Netzwerks vor und wird auf die gewichtete Summe aus Inputwerten des Neurons angewandt. Dadurch, dass die Aktivierungsfunktion nicht linear ist, kann auch das Perceptron nicht-lineare Zusammenhänge erlernen.

Somit erhalten die Neuronalen Netze erst die Eigenschaft auch komplexe Zusammenhänge erlernen und abbilden zu können. Ohne die nicht-lineare Funktion könnten nämlich nur lineare Abhängigkeiten zwischen den gewichteten Inputwerten und den Outputwerten hergestellt werden. Dann könnte man jedoch auch gleich eine Lineare Regression nutzen. Die Abläufe innerhalb eines Perceptrons werden dabei im Folgenden kurz beschrieben.

Das Perceptron hat mehrere Eingänge, die sogenannten Inputs, an denen es numerische Informationen, also Zahlenwerte erhält. Je nach Anwendung kann sich die Zahl der Inputs unterscheiden. Die Eingaben haben verschiedene Gewichte, die angeben, wie einflussreich die Inputs für die schlussendliche Ausgabe sind. Während des Lernprozesses werden die Gewichte so geändert, dass möglichst gute Ergebnisse entstehen.

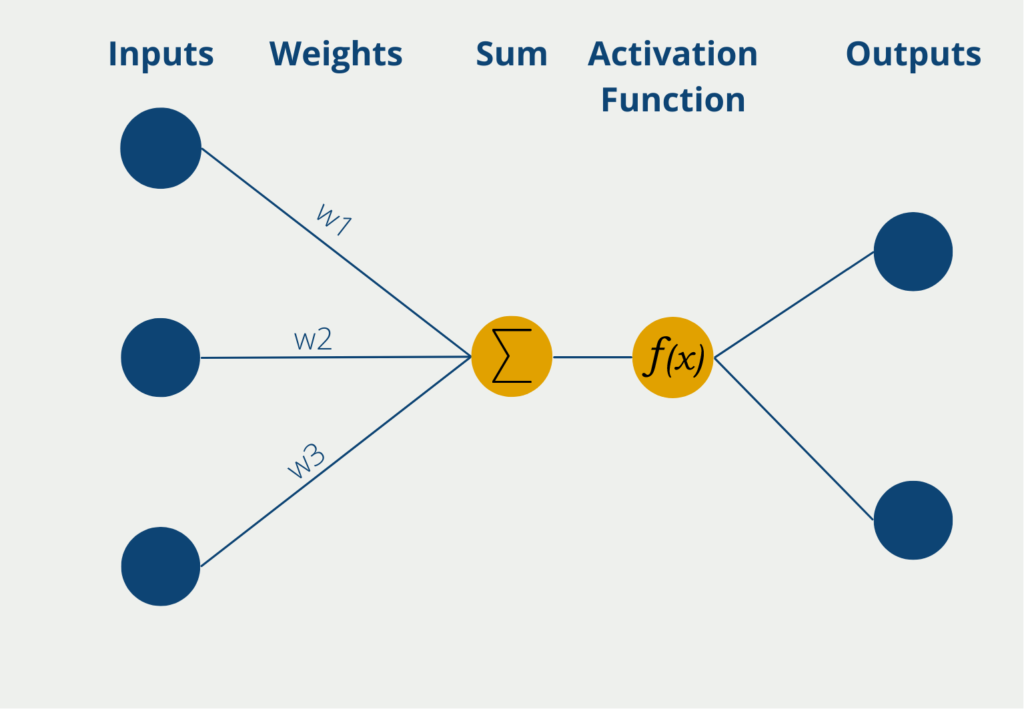
Das Neuron selbst bildet dann die Summe der Inputwerte multipliziert mit den Gewichten der Inputs. Diese gewichtete Summe wird weitergeleitet an die sogenannte Aktivierungsfunktion. In der einfachsten Form eines Neurons gibt es genau zwei Ausgaben, es können also nur binäre Outputs vorhergesagt werden, beispielsweise “Ja” oder “Nein” oder “Aktiv” oder “Inaktiv” etc.

Wenn das Neuron binäre Ausgabewerte hat, wird eine Aktivierungsfunktion genutzt, deren Werte auch zwischen 0 und 1 liegen. Somit ergeben sich dann die Ausgabewerte direkt durch die Nutzung der Funktion.

Was ist die Softmax-Funktion?

Der Softmax ist eine mathematische Funktion, die einen Vektor als Input nimmt und dessen einzelne Werte in Wahrscheinlichkeiten umwandelt, abhängig von deren Größe. Ein hoher numerischer Wert führt dabei zu einer hohen Wahrscheinlichkeit im resultierenden Vektor.

In Worten gesprochen, wird jeder Wert des Vektors durch die Summe aller Werte des Ausgangsvektors geteilt und im neuen Vektor abgelegt. Rein mathematisch sieht diese Formel dann so aus:

\(\) \[\sigma (x)_{j} = \frac{e^{z_{j}}}{\sum_{k=1}^{K} e^{z_{k}}} \text{for } j = 1, …, K.\]

Mit einem konkreten Beispiel wird die Funktionsweise der Softmax-Funktion deutlicher:

\(\) \[\begin{pmatrix}1 \\ 2 \\3 \end{pmatrix} \underrightarrow{Softmax} \begin{pmatrix}\frac{1}{1 + 2 + 3} \\ \frac{2}{1 + 2 + 3} \\ \frac{3}{1 + 2 + 3} \end{pmatrix} = \begin{pmatrix} 0.166 \\ 0.33 \\ 0.5 \end{pmatrix} \]

Das positive Merkmal dieser Funktion ist, dass dafür gesorgt wird, dass die Summe der Ausgabewerte immer kleiner oder gleich 1 sind. Das ist vor allem in der Wahrscheinlichkeitsrechnung sehr von Vorteil, da so gewährleistet ist, dass keine addierte Wahrscheinlichkeit größer 1 herauskommen kann.

Welche Aktivierungsfunktionen gibt es?

Es gibt viele verschiedene Aktivierungsfunktionen, die im Bereich des Machine Learnings zum Einsatz kommen. Zu den häufigsten zählen:

• Sigmoid-Funktion: Diese Funktion bildet die Eingangswerte auf den Bereich zwischen 0 und 1 ab.
• Tanh-Funktion: Die Tanh-Funktion, oder Tangens – Hyperbolicus ausgeschrieben, mappt die Eingangswerte auf den Bereich zwischen -1 und 1.
• ReLU-Funktion: Die Rectified Linear Unit, oder kurz ReLu-Funktion, nimmt den Eingabewert nur dann, wenn er größer oder gleich Null ist. Ansonsten wird der Ausgabewert auf Null gesetzt.
• Softmax-Funktion: Die Softmax-Funktion bildet die Eingangswerte auch auf den Bereich zwischen 0 und 1 ab, ist aber besonders geeignet für die letzte Schicht im Neuronalen Netzwerk, um dort eine Wahrscheinlichkeitsverteilung darzustellen.

Was ist der Unterschied zwischen Sigmoid und Softmax?

Auf den ersten Blick erscheinen die Sigmoid- und die Softmax-Funktion relativ ähnlich, da beide Funktionen den Eingangswert auf den Zahlenbereich zwischen 0 und 1 abbilden. Auch deren Verlauf ist nahezu identisch mit dem Unterschied, dass die Sigmoid-Funktion bei x = 0 den Wert 0,5 durchläuft und die Softmax-Funktion an diesem Punkt noch unterhalb von 0,5 liegt.

Der Unterschied zwischen den Funktionen liegt in der Anwendung. Die Sigmoid-Funktion kann für binäre Klassifikationen genutzt werden, also für Modelle, in denen zwischen zwei unterschiedlichen Klassen entschieden werden soll. Der Softmax hingegen kann auch für Klassifikationen genutzt werden, die mehr als zwei Klassen vorhersagen sollen. Dabei stellt die Funktion sicher, dass die Wahrscheinlichkeit aller Klassen 1 ergibt.

Tatsächlich lässt sich auch mathematisch nachweisen, dass im Fall von zwei Klassen, die Sigmoid- und die Softmax-Funktion übereinstimmen.

Welche Machine Learning Algorithmen nutzen den Softmax?

Wie wir bereits erfahren haben, wird die Softmax-Funktion vor allem für Multi-Klassifizierungsprobleme eingesetzt. Folgende Modelle und Algorithmen greifen dabei auf die Funktion zurück:

• Neuronale Netzwerke: Die letzte Schicht des Netzwerks hat eine Softmax-Aktivierungsfunktion, wenn zwischen mehr als zwei Klassen entschieden werden soll.
• Reinforcement Learning: Im Bereich des Bestärkenden Lernens muss das Modell häufig zwischen mehreren Aktionen entscheiden. Auch dazu wird die Funktion eingesetzt.
• Logistische Regression: Die “normale” logistische Regression geht eigentlich von zwei Klassen aus, die unterschieden werden. Mithilfe der Softmax-Funktion lassen sich auch Modelle aufbauen, die mehr als zwei Gruppen klassifizieren können.

Was sind die Grenzen der Softmax-Funktion?

Die Softmax-Funktion ist ein leistungsfähiges Werkzeug für probabilistische Modellierungs- und Klassifizierungsaufgaben. Sie hat jedoch auch bestimmte Einschränkungen und Überlegungen, die berücksichtigt werden sollten:

• Empfindlichkeit gegenüber Ausreißern: Die Softmax-Funktion kann empfindlich auf Ausreißer in den Eingabedaten reagieren. Extremwerte können sich erheblich auf die resultierenden Wahrscheinlichkeiten auswirken und die Klassifizierungsergebnisse möglicherweise verfälschen.
• Unausgewogenheit der Klassen: Es wird davon ausgegangen, dass die Klassen ausgewogen sind, d. h. dass jede Klasse in den Trainingsdaten gleich stark vertreten ist. In Situationen, in denen ein erhebliches Klassenungleichgewicht besteht, kann die Softmax-Funktion Schwierigkeiten haben, den Minderheitsklassen angemessene Wahrscheinlichkeiten zuzuweisen.
• Mangelnde Robustheit gegenüber sich überschneidenden Klassen: Wenn die Entscheidungsgrenzen zwischen den Klassen nicht klar definiert sind und sich die Klassen im Merkmalsraum überschneiden, kann die Softmax-Funktion Schwierigkeiten haben, den verschiedenen Klassen genaue Wahrscheinlichkeiten zuzuweisen.
• Unfähigkeit zur Erfassung von Unsicherheiten: Die Funktion erzeugt sichere Wahrscheinlichkeiten für jede Klasse, selbst wenn das Vertrauen des Modells in seine Vorhersagen gering ist. Sie erfasst nicht explizit die Unsicherheit oder Mehrdeutigkeit der Klassifizierungsaufgabe.
• Eingabe-Skalierung: Die Softmax-Funktion reagiert empfindlich auf die Skalierung der Eingabewerte. Wenn die Eingabewerte nicht richtig skaliert sind, kann dies die relativen Größen der resultierenden Wahrscheinlichkeiten beeinflussen und sich möglicherweise auf die Klassifizierungsgenauigkeit auswirken.
• Mangel an interpretierbaren Wahrscheinlichkeiten: Softmax-Wahrscheinlichkeiten liefern zwar relative Rangfolgen zwischen den Klassen, entsprechen aber nicht immer den tatsächlichen Wahrscheinlichkeiten in der realen Welt. Die Wahrscheinlichkeiten sind möglicherweise nicht leicht zu interpretieren, insbesondere wenn das Modell auf verzerrten oder begrenzten Daten trainiert wurde.
• Alternative Entscheidungsgrenzen: Softmax weist Wahrscheinlichkeiten auf der Grundlage einer Entscheidungsgrenze zu, und kleine Änderungen in den Eingabedaten können zu unterschiedlichen Klassifizierungen führen. Dies bedeutet, dass die Entscheidungsgrenzen nicht unbedingt stabil oder eindeutig sind.

Es ist wichtig, sich dieser Einschränkungen bewusst zu sein und sie bei der Verwendung der Softmax-Funktion in der Praxis zu berücksichtigen. Je nach spezifischem Problem und Anforderungen können alternative Ansätze wie probabilistische Klassifizierungsmethoden oder Modelle, die explizit mit Klassenungleichgewicht und Unsicherheit umgehen, besser geeignet sein.

Wie verwendet man die Softmax-Funktion in Python?

In Python wird die Softmax-Funktion in der Regel mit der NumPy-Bibliothek implementiert. NumPy bietet effiziente mathematische Operationen für Arrays und eignet sich daher für die Berechnung der Funktion für mehrere Klassen. Hier ist ein Beispiel dafür, wie die Softmax-Funktion in Python implementiert werden kann:

In dieser Implementierung wird davon ausgegangen, dass die Eingabe x ein 2D-Array ist, bei dem jede Zeile eine Stichprobe darstellt und jede Spalte die Punktzahl oder den Logit für eine bestimmte Klasse repräsentiert. Die Funktion berechnet den Exponentialwert für jedes Element x, um den Zähler der Softmax-Gleichung zu erhalten. Anschließend werden die Exponentialwerte entlang der entsprechenden Achse (Achse=1) summiert, um den Nenner zu berechnen. Schließlich werden die Wahrscheinlichkeiten erhalten, indem jedes Element des Zählers durch den Nenner geteilt wird.

Die Implementierung nutzt die Broadcasting-Funktion von NumPy, um elementweise Operationen über Arrays hinweg effizient durchzuführen. Dadurch kann die Funktion auf mehrere Stichproben gleichzeitig angewendet werden.

Es ist erwähnenswert, dass die hier vorgestellte Implementierung von einer Standard-Softmax-Funktion ausgeht, die auf Logits oder Scores operiert. Wenn Sie mit großen Werten arbeiten oder numerische Stabilitätsprobleme behandeln müssen, können Sie zusätzliche Techniken in Betracht ziehen, wie das Subtrahieren des Maximalwertes von jeder Zeile von x vor dem Potenzieren (x – np.max(x, axis=1, keepdims=True)), um einen Überlauf zu verhindern.

Zusätzlich bietet TensorFlow seine eigene Implementierung der Softmax-Funktion, die besonders nützlich ist, wenn man mit neuronalen Netzen und Deep Learning Modellen arbeitet.

Um sie zu verwenden, können Sie die eingebaute Funktion tf.nn.softmax() nutzen. Hier ist ein Beispiel, wie man sie benutzt:

In diesem Beispiel wird die TensorFlow-Funktion tf.nn.softmax() auf den Logits-Tensor angewendet, der die Punktzahlen oder Logits für jede Klasse darstellt. Die Funktion berechnet die Wahrscheinlichkeiten basierend auf den eingegebenen Logits.

Die Verwendung der TensorFlow-Implementierung der Funktion bietet den Vorteil, dass sie sich nahtlos in andere TensorFlow-Operationen integrieren lässt und die Funktion in neuronalen Netzwerkarchitekturen verwendet werden kann. Sie bietet auch eine automatische Differenzierung für das Training von Deep-Learning-Modellen mit Techniken wie Backpropagation.

Durch die Kombination der Flexibilität von TensorFlow mit der Softmax-Funktion können Sie die Berechnungen einfach in Ihre Machine Learning Pipelines einbinden und die Vorteile der umfangreichen Funktionen und Optimierungen von TensorFlow nutzen.

Das solltest Du mitnehmen

• Die Softmax-Funktion stammt aus der Mathematik und bildet Eingangswerte in den Bereich [0, 1] ab.
• Sie ist dabei sehr ähnlich zu der Sigmoid-Funktion mit dem Unterschied, dass bei mehr als zwei Klassen, die Wahrscheinlichkeiten sich zu 1 aufaddieren.
• Im Machine Learning werden auch andere Aktivierungsfunktionen genutzt, wie beispielsweise die tanh- oder die ReLU Funktion.

Andere Beiträge zum Thema Softmax

• Einen anderen, interessanten Beitrag zur Softmax-Aktivierungsfunktion findest Du hier.