Der Median spielt eine zentrale Rolle in der Statistik und der Datenanalyse, da er als Maß der zentralen Tendenz eines Datensatzes genutzt werden kann. Er ist dabei der Wert im Datensatz, welcher die Mitte bildet und die Zahlen in zwei gleich große Teile teilt. Im Vergleich zum Mittelwert ist er nicht anfällig gegenüber Ausreißern und liefert dadurch auch bei ungleich verteilten Daten ein zuverlässiges Bild der zentralen Lage. Aufgrund von dieser Eigenschaft wird die Kennzahl in den verschiedensten Bereichen, wie beispielsweise der Medizin, den Sozialwissenschaften oder der Wirtschaft eingesetzt. 

In diesem Beitrag erklären wir alle Einzelheiten rund um den Median und gehen im Detail auf die Berechnung dieser Kennzahl mithilfe von unterschiedlichen Beispielen ein. Außerdem vergleichen wir ihn mit anderen statistischen Kennzahlen wie dem Mittelwert oder dem Modus und zeigen auf, welche Anwendungen ihn einsetzen. Zu einem vollständigen Bild gehört es auch, die Vor- und Nachteile dieser Kennzahl im Detail zu erläutern, damit man eine informierte Entscheidung treffen kann, ob der Einsatz gerechtfertigt ist. Abschließend schauen wir uns an, wie man die Kennzahl in Python oder Excel berechnen kann. 

Was ist der Median?

Der Median ist eine statistische Kennzahl, welche eine Aussage über die zentrale Tendenz des Datensatzes liefert. Es ist der Wert, welcher genau in der Mitte einer geordneten Datenreihe liegt, sodass alle Elemente in der einen Hälfte des Datensatzes kleiner als der Median sind und alle Elemente in der anderen Hälfte des Datensatzes entsprechend größer. Durch diese Eigenschaft wird er zu einer robusten Wahl, da er auch bei ungleichmäßig verteilten Daten identisch bleibt. Der Median ändert sich nämlich nicht, wenn sich die konkreten Werte der unteren Hälfte verändern, solange die Anzahl der Werte gleichbleibt und sie alle weiterhin kleiner sind als der Medianwert. Dadurch haben auch extreme Ausreißer erstmal keinen größeren Einfluss. 

Der Mittelwert hingegen berechnet den arithmetischen Durchschnitt des Datensatzes, anstatt die Mitte des Datensatzes zu finden. Dadurch haben Datenpunkte mit extrem großen oder kleinen Werten einen starken Einfluss auf den Durchschnitt. Der Median wird in verschiedensten Anwendungen verwendet, in denen es zu Ausreißern kommen kann, um eine realistischere Einschätzung der zentralen Lage zu bekommen. Bei Einkommenserhebungen beispielsweise unterscheiden sich beide Kennzahlen teilweise sehr deutlich. 

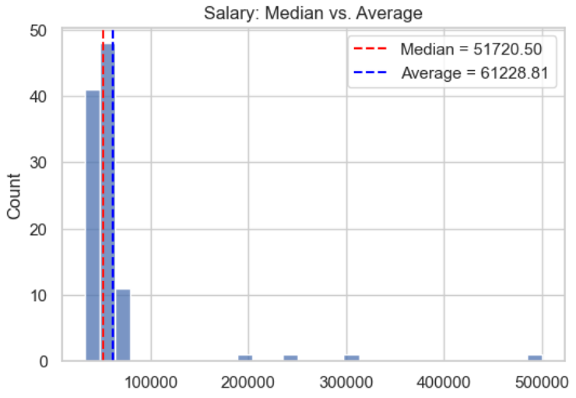
In diesem Diagramm sind die Gehälter von mehr als einhundert Personen dargestellt. Man erkennt, dass ein Großteil der Befragten, nämlich etwa fünfzig Personen, ein jährliches Gehalt von etwa $50.000 haben. Jedoch gibt es auch ein paar Ausreißer von Angestellten mit einem viel höheren Gehalt von $200.000 bis zu $500.000. Der Durchschnitt reagiert auf diese Personen deutlich stärker und gibt das durchschnittliche Gehalt mit etwa $60.000 an, während der Median gegenüber den Ausreißern robuster ist und richtigerweise erkennt, dass der Großteil der Personen weniger als $60.000 verdient. 

Wie berechnet sich der Median?

Der Median ist der mittlere Wert in einer Datenreihe und kann abhängig von der Größe der Datenreihe, ein Wert aus der Menge sein oder auch ein Wert, der nicht in der Menge direkt vorkommt. Im ersten Schritt der Berechnung wird die Datenreihe der Größe nach aufsteigend sortiert. Wenn dies geschehen ist, hängt die weitere Berechnung davon ab, ob die Anzahl der Elemente gerade oder ungerade ist. 

Datenmengen mit einer ungeraden Anzahl an Elementen

Bei einer ungeraden Anzahl von Elementen in der Datenreihe ist die Berechnung des Medians deutlich einfacher. Dazu wird aus der sortierten Datenreihe einfach der Wert genommen, der genau in der Mitte liegt. Dadurch, dass die Anzahl ungerade ist, ist auch sichergestellt, dass ein solcher Wert existiert. 

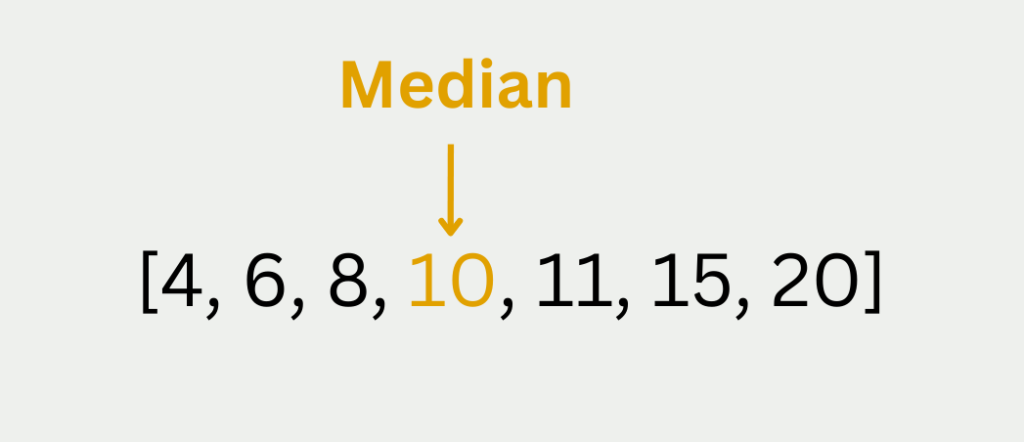
In der Datenreihe [3,7,9] beispielsweise liegt die 7 genau in der Mitte, da es genau einen Wert gibt, der größer ist, und genau einen Wert der kleiner ist. Somit ist der Median dieser Datenreihe 7. Die Datenreihe [3,7,9,13,18] hat fünf Elemente und somit auch eine ungerade Größe. In diesem Fall liegt die 9 genau in der Mitte der Datenreihe und somit ist das Ergebnis 9. 

Datenmengen mit einer geraden Anzahl an Elementen

Bei einer geraden Anzahl an Elementen kann der gerade beschriebene Ansatz nicht genutzt werden, weil es keinen Datenpunkt gibt, welcher genau in der Mitte der Datenreihe liegt. Bei der Datenreihe [3,7,9,11] beispielsweise ist dieser Mittelpunkt nicht vorhanden. Deshalb muss man sich behelfen, indem man die beiden mittleren Werte, also in diesem Fall 7 und 9, verwendet und daraus den Durchschnitt, also (7+9)/2 = 8, berechnet. Der Median in dieser Datenreihe liegt also bei 8. 

Durch diese Vorgehensweise wird deutlich, warum der Median robust gegenüber Ausreißern ist, da die Werte außerhalb der Mitte für die Berechnung nicht relevant sind, solange sie die Reihenfolge der einzelnen Elemente nicht verändern. Wenn wir beispielsweise die Reihe [3,7,9] verwenden, bleibt die 7 der Median, auch wenn sich der Wert der beiden anderen Elemente stark verändert. Dadurch ist 7 auch die Mitte der Datenreihe [1,7,100] und sie ist auch der Median der Datenreihe [0.001,7,10000].

Zusammenfassen lassen sich diese beiden Fälle mithilfe der folgenden Formel:

\(\)\[
\text{Median} =
\begin{cases}
x_{\frac{n+1}{2}}, & \text{wenn } n \text{ ungerade} \\[10pt]
\frac{x_{\frac{n}{2}} + x_{\frac{n}{2} + 1}}{2}, & \text{wenn } n \text{ gerade}
\end{cases}
\]

Was sind Median, Modus und Mittelwert und wie unterscheiden sie sich?

Der Median, Modus und Mittelwert sind unterschiedliche Kennzahlen, welche verschiedene Aspekte der „Mitte“ eines Datensatzes beschreiben. Abhängig von der Art und den Eigenschaften der Daten hat jedes dieser Maße seine eigenen Vor- und Nachteile, die wir in diesem Abschnitt genauer beleuchten. Ein zentraler Aspekt für die Wahl des geeigneten Maßes ist dabei auch die Verteilung der Daten, welche beispielsweise beinhaltet, ob Ausreißer vorhanden sind. 

Mittelwert

Der Mittelwert berechnet sich, indem alle Datenpunkte in einem Datensatz addiert werden und anschließend durch die Anzahl der Daten geteilt werden. Dadurch dient er als eine Art Balancepunkt des Datensatzes. Diese Berechnung macht den Mittelwert jedoch auch anfällig für Ausreißer, also besonders hohe oder niedrige Werte, und für ungleichmäßige Verteilungen. In diesen Fällen gibt der Mittelwert möglicherweise kein genaues Bild über den Datensatz ab. 

Da der Mittelwert alle Werte zu gleichem Gewicht in die Berechnung mit aufnimmt, kann ein einzelner extrem hoher oder niedriger Wert den Durchschnitt stark beeinflussen. Ein solcher Wert kann somit dazu führen, dass der Mittelpunkt nicht mehr die typische Mitte des Datensatzes repräsentiert. Dadurch ist der Mittelwert ungeeignet für asymmetrische oder verzerrte Daten. 

Beispiel: Angenommen wir haben einen Datensatz über die Einkommensverteilung in einer kleinen Gruppe. Dabei werden die folgenden Einkommen ermittelt: [30.000, 32.000, 35.000, 500.000]. Von der Betrachtung der Daten würden wir rein nach dem Gefühl davon ausgehen, dass eine „durchschnittliche Person“ in diesem Datensatz etwa zwischen 32.000 und 35.000 verdient. Durch den sehr starken Ausreißer jedoch erhalten wir einen errechneten Durchschnitt von (30.000 + 32.000 + 35.000 + 500.000) / 4 = 149.250. Dieser Wert ist jedoch viel höher als die typischen Einkommen, die wir im Datensatz beobachten, was sich auf das höchste Einkommen von 500.000 zurückführen lässt. 

Aufgrund von diesen Eigenschaften ist der Mittelwert besonders für normalverteilte Daten, ohne extreme Ausreißer geeignet, wie sie zum Beispiel in der Chemie, der Physik oder der Finanzanalyse vorkommen. Diese können häufig auf eine gleichmäßige Verteilung der Daten zurückgreifen. 

Median

Der Median ist der mittlere Wert einer Datenreihe und teilt den Datensatz so, dass die Hälfte der Daten oberhalb und die andere Hälfte unterhalb liegt. Durch diese Eigenschaft ist diese Kennzahl deutlich unempfindlicher gegenüber Ausreißern bzw. stark abweichenden Datenpunkten, da für sie lediglich die Lage der extremen Datenpunkte eine Rolle spielt und jedoch nicht deren absolute Höhe. Für das obige Einkommensbeispiel ergibt sich dadurch, dass der Median genau zwischen 32.000 und 35.000 liegen muss, da dort die Mitte des Datensatzes ist. Somit ergibt sich ein Wert von (32.000 + 35.000) / 2  = 33.500. Dieser gibt eine realistischere Aussage über die Mitte der Datenverteilung im Vergleich zum Mittelwert, da er nicht von dem Ausreißereinkommen verzerrt wird. 

Aufgrund von dieser Eigenschaft wird der Median vor allem in Anwendungen genutzt, in denen Daten oftmals verzerrt und Ausreißer eine große Rolle spielen, wie etwa in der Einkommensstatistik, bei Immobilienpreisen oder bei medizinischen Daten. 

Modus 

Der Modus unterscheidet sich von den beiden bisher vorgestellten Kennzahlen und umschreibt den häufigsten Wert in einer Datenreihe. Damit ist er ein Maß der zentralen Tendenz, welches sich ausschließlich mit der Häufigkeit von Werten beschäftigt. Diese Eigenschaft ermöglicht es, dass der Modus als einziges auch für nominale Daten, also solche, welche nicht numerisch sind, eingesetzt werden kann. 

Der Modus wird häufig in Umfragen und in der Marktforschung genutzt, da er die Möglichkeit bietet, die häufigsten Antworten oder beliebte Produkte zu identifizieren. Hierbei wird jedoch auch das Hauptproblem des Modus deutlich, nämlich, wenn eine Reihe mehrdeutig ist, sodass zwei Werte in der Umfrage genau gleichhäufig vorkommen. Wenn beispielsweise bei einer Umfrage der beliebtesten Automarken sowohl „Audi“ als auch „BMW“ gleich häufig genannt werden, dann spricht man davon, dass die Datenreihe bimodal ist, da genau zwei Kategorien am häufigsten vorkommen. Bei einer multimodalen Datenreihe gibt es sogar mehr als zwei Werte, welche am häufigsten in der Umfrage genannt wurden. 

Insgesamt bietet die folgende Grafik eine gute Möglichkeit, um eine schnelle Entscheidung für eine der Kennzahlen treffen zu können:

Der Median bietet im Vergleich zum Mittelwert und zum Modus eine ausgewogene Möglichkeit, die zentrale Tendenz eines Datensatzes numerisch auszudrücken. Vor allem bei verzerrten Daten mit Ausreißern weist er Stärken auf, da er sich von diesen nicht beeinflussen lässt, solange der mittlere Wert des Datensatzes derselbe bleibt. Der Mittelwert hingegen ist bei normalverteilten Daten, ohne die Gefahr von Ausreißern, besser geeignet und der Modus kann auch für nominale Datensätze genutzt werden.

Was sind die Vor- und Nachteile des Medians?

Der Median ist ein häufig verwendetes Maß zur Bestimmung der zentralen Tendenz eines Datensatzes. In diesem Artikel haben wir bereits einige Vor- und Nachteile genannt, die die Verwendung dieser Kennzahl mit sich bringen. In diesem Abschnitt wollen wir die Punkte nochmals übersichtlich zusammenfassen und auch ein paar neue Aspekte mit aufnehmen. 

Vorteile

• Robustheit gegenüber Ausreißern: Wie bereits mehrfach erläutert, besteht der Hauptvorteil des Medians darin, dass er sich auch bei extremen Werten und Ausreißern nicht oder nur wenig verändert und im Gegensatz zum Mittelwert deutlich robuster gegenüber diesen Erscheinungen ist. Da er sich allein auf die Position der Daten bezieht, spielt die Höhe der Daten und deren Unterschiede lediglich eine untergeordnete Rolle.  
• Bessere Repräsentation bei schiefen Verteilungen: Bei schiefen Verteilungen, wie der Einkommensstatistik oder bei Immobilienpreisen, stellt der Median häufig ein realistischeres Bild dar im Vergleich zum Mittelwert. Solche Daten sind oft rechtsschief, wodurch der Mittelwert unnatürlich nach oben gezogen wird und dadurch eine bessere Mitte der Daten dargestellt werden kann.  
• Transformationsinvariant: Der Median ist zwar ein nicht-linearer Maßstab, jedoch wird er durch monotone Transformationen nicht verändert. Lineare Transformationen, wie zum Beispiel die Multiplikation aller Datensatzwerte mit einer festen Konstanten oder die Addition eines festen Wertes, verändern den Mittelwert direkt. Jedoch bleibt dadurch die Reihenfolge des Datensatzes dieselbe, sodass sich der Wert nicht verändert. Somit kann zum Beispiel der Datensatz logarithmiert werden und der neue Wert entspricht dann einfach dem Logarithmus des alten Medians.  
• Leichte Interpretation: Diese Kennzahl lässt sich auch bei großen Datensätzen schnell und einfach interpretieren und kann dadurch von einem fachfremden Publikum einfach verstanden werden. Durch die Berechnungsweise ist er deutlich unkomplizierter, was beispielsweise in Berichten oder Präsentationen eine höhere Akzeptanz beim Publikum hervorruft. 
• Nutzung bei ordinalen Daten: Schließlich kann der Median, anders als der Durchschnitt, auch bei ordinalen Daten mit Bewertungsskalen oder Rangfolgen genutzt werden, wodurch er deutlich flexibler einsetzbar ist. Etwa in der Marktforschung ist dies ein weiterer Vorteil, der es möglich macht, dass die Daten weder messbar noch intervallskaliert sein müssen. 

Nachteile

• Verlust von Details: Da der Median sich lediglich an der Lage der Daten orientiert und die Abstände der Datenpunkte nicht beachtet, verliert diese Kennzahl wichtige Informationen über die Lage und die Verteilung der Daten. In Verteilungen, in denen die Abstände eine wichtige Rolle spielen, wie beispielsweise bei Messwerten in wissenschaftlichen Experimenten, ist dies ein Ausschlusskriterium. 
• Empfindlichkeit bei Datenänderungen in geraden Datensätzen: Bei geraden Datensätzen wird der Median als Durchschnitt aus den beiden mittleren Datenpunkten errechnet. Dadurch kann er in einem solchen Szenario anfällig für Datenänderungen sein, gerade dann, wenn die Stichprobe besonders klein ist. 
• Begrenzte Aussagekraft bei normalverteilten Daten: Bei normalverteilten oder symmetrischen Daten unterscheidet sich der Median kaum vom Mittelwert, da Ausreißer nur eine untergeordnete Rolle spielen. Da beide Werte dann nahezu identisch sind, bietet der Median keinerlei Vorteile und es kann sogar passieren, dass er weniger Informationen über die Verteilung selbst vermittelt. Der Mittelwert hingegen kann zusammen mit der Standardabweichung bereits wichtige Eigenschaften der Verteilung beschreiben. 
• Fehlende Anwendbarkeit bei statistischen Tests: Viele statistische Tests, wie beispielsweise der t-Test oder die Varianzanalyse, setzen auf den Mittelwert als Maß für die zentrale Tendenz. Der Median ist hierbei oft nicht anwendbar und er müsste erst aufwendig transformiert werden, um für diese inferenzstatistischen Tests anwendbar zu sein.  
• Nicht geeignet für alle Arten von Daten: Obwohl der Median in vielen Anwendungen von großem Nutzen sein kann, kann er in Einzelfällen nur eine begrenzte Aussagekraft besitzen. Zum Beispiel bei multimodalen Verteilungen, also wenn die Daten mehrere Cluster von Werten besitzen, repräsentiert der Median nicht unbedingt den zentralen Punkt, welcher alle Cluster gleichermaßen berücksichtigt. 

Der Median hat genau wie andere statistische Kennzahlen auch, Vor- und Nachteile, welche vor der Nutzung abgewogen werden sollten. Die Hauptvorteile liegen darin, dass er nicht so stark auf Ausreißer reagiert, wie der Mittelwert, und dadurch ein besseres Bild der zentralen Tendenz liefern kann. In normalverteilten Datenverteilungen jedoch, unterscheidet er sich kaum vom Mittelwert und es gehen hingegen noch Informationen zu den Abständen zwischen den Datenpunkten verloren. 

Welche Herausforderungen ergeben sich durch den Median und wie können sie gelöst werden?

Vor allem bei der Arbeit mit großen Datenmengen und in speziellen Datenkontexten, kann die Arbeit mit dem Median Herausforderungen mit sich bringen. In diesem Abschnitt befassen wir uns mit einigen Szenarien und wie effektiv mit diesen umgegangen werden kann. 

Effizienz bei großen Datenmengen

Der Median basiert darauf, dass eine Liste an Werten erst sortiert werden muss und anschließend das mittlere Element aus dieser Liste gewählt wird. Bei sehr großen Datenmengen kann diese Aufgabe sehr rechenaufwendig werden und viel Zeit in Anspruch nehmen. Damit der Median trotzdem effizient berechnet werden kann, wird der sogenannte QuickSelect Algorithmus verwendet, welcher eine effiziente Methode bietet, um das \(k\)-kleinste Element in einer unsortierten Liste zu finden. Dadurch erspart man sich das Sortieren der Liste, was im Durchschnitt \(O(nlogn)\) Zeit erfordert. Der QuickSelect Algorithmus hingegen arbeitet mit der durchschnittlichen linearen Zeit (\(O(n)\)).

Dazu wird ein beliebiges Element, das sogenante Pivot-Element, aus der Liste gewählt. Ähnlich wie bei QuickSort wird anschließend die Liste um dieses Element partioniert, sodass alle Elemente, die kleiner sind als das Pivot in die linke Partition gelangen und alle Elemente die größer als das Pivot sind in die rechte Partition gelangen. Durch diese Partitionierung erfährt man, wie viele Element kleiner als das Pivot sind. 

Angenommen \(m\) ist die Anzahl der Elemente in der linken Partition, dann ergeben sich die folgenden drei Fälle: 

• \(k = m+1\): In der linken Partition befinden sich genau \(k-1\) – Elemente. Somit wurde zufälligerweise bereits der Median als Pivot gewählt. 
• \(k \leq m\): Der gesuchte Median liegt somit in der linken Partition, da in der linken Partition mehr als k-Werte sind und somit auch Werte in der linken Partition sind, die noch größer als k sind. Deshalb kann der Algorithmus rekursiv auf der linken Partition angewendet werden.
• \(k \geq m+1\): In diesem Fall sind in der linken Partition weniger als k-Werte, sodass der gesuchte Wert in der rechten Partition liegen muss. Der Algorithmus wird deshalb rekursiv auf die rechte Partition angewendet. 

Durch diese Vorgehensweise wird der Zeitaufwand für die Berechnung deutlich verringert und es können Datensätze mit unterschiedlichen Größen effizient verarbeitet werden. 

Median in gruppierten Häufigkeitsverteilungen

In gruppierten Datensätzen liegen die einzelnen Werte des Datensatzes nicht vor, sondern es werden nur die gruppierten Häufigkeitsverteilungen gegeben, also die Anzahl von Werten in einer Klasse. Ein häufiges Beispiel ist die Auswertung von Schulnoten, bei der nicht die einzelnen Noten bekannt sind, sondern lediglich angegeben ist, wie viele Schüler Noten im Bereich zwischen 1 und 2 erzielt haben. Dadurch lässt sich der Median nicht einfach ablesen. 

Um dieses Problem zu lösen, wird für jede Klasse die kumulative Häufigkeit berechnet, indem man die Häufigkeiten der Klassen sukzessive aufsummiert. Anschließend bestimmt man die Anzahl der Gesamtbeobachtungen, also die Größe des Datensatzes, und teilt diese durch zwei. Der Median liegt dann in dieser Gruppe, in der die kumulative Häufigkeit zum ersten Mal diesen Schwellenschwert überschreitet.   

Median mit gewichteten Daten

In gewichteten Datensätze erhalten die einzelnen Datenpunkte unterschiedliche Gewichtungen, um eine Verzerrung im Datensatz zu verhindern. Wenn man beispielsweise eine Befragung über alle Altersgruppen hinweg machen will, jedoch aufgrund der Befragungsweise nur sehr wenige ältere Menschen befragen konnte, dann erhalten die wenigen Senioren, die befragt werden konnten, eine höhere Gewichtung im Datensatz, sodass es nicht zu einer Verzerrung hin zu den jüngeren Befragten kommen kann. Für einen solchen Datensatz muss dann entsprechend der gewichtete Median bestimmt werden. 

Dieser wird so festgelegt, dass unterhalb etwa 50 % der Gesamtgewichte liegen und oberhalb auch etwa 50 % der Gesamtgewichte. Abhängig vom Datensatz kann es passieren, dass die genaue Mitte nicht gefunden werden kann. Deshalb muss mit dieser Näherung gearbeitet werden. 

Durch den Einsatz dieser Methoden kann der Median auch bei speziellen Datensätzen angewendet werden, welche gruppiert, gewichtet oder einfach sehr groß sind. 

Wie kann man den Median in Python, Excel und anderen Programmen berechnen?

Die Berechnung des Medians ist ein wichtiger Schritt in vielen statistischen Analysen und kann mithilfe von Python oder Excel einfach und schnell umgesetzt werden. In diesem Abschnitt schauen wir uns die Berechnung in unkomplizierten Beispielen genauer an. 

Medianberechnung in Excel

In Excel kann die Berechnung des Medians einfach mithilfe einer Funktion umgesetzt werden. Dazu kann man beispielsweise die Einkommen in einem Datensatz in einer Spalte sammeln und in einer neuen Zelle die Funktion anwenden, indem man den Bereich definiert, in dem die Zahlen abgelegt sind. 

In unserem Fall haben wir zehn Einkommensdaten in der Spalte A abgelegt und mit der Überschrift „Incomes“ überschrieben. Entsprechend sind also die Zahlenwerte in den Zelle A2 bis A11 hinterlegt. 

Der Median kann nun in einer neuen Zelle berechnet werden, indem die Funktion aufgerufen wird.

In den runden Klammern definieren wir den Zahlenbereich, in dem die Einkommen hinterlegt sind und erhalten, nachdem wir die ENTER-Taste drücken das schlussendliche Ergebnis. 

Mithilfe von diesen einfachen Schritten, kann in Excel schnell die Kennzahl für eine Datenreihe berechnet werden. 

Medianberechnung in Python

In Python kann man verschiedene Bibliotheken für die Berechnung des Medians nutzen, wie beispielsweise NumPy oder Pandas. In NumPy hinterlegt man dafür die Daten in einer Liste und nutzt dann die dazugehörige Funktion, welcher die Liste dann übergeben wird. 

Die Nutzung von NumPy kann vor allem bei großen Datenmengen effizient sein, da die Berechnung speziell optimiert wurde. Wenn die Daten hingegen in einem DataFrame gespeichert sind, ist die Verwendung von Pandas naheliegend. Diese Bibliothek liefert bereits die Funktion, welche direkt auf eine DataFrame Spalte angewandt werden kann. 

Medianberechnung in R

In R kann diese Kennzahl direkt genutzt werden, ohne dass man dafür eine Bibliothek importieren muss. Dafür werden die Werte des Datensatzes einfach in einem Vektor abgelegt. Anschließend kann die Kennzahl dann mithilfe der vorliegenden Funktion ermittelt werden. 

data <- c(3, 7, 2, 9, 5)

median_value <- median(data)

print(median_value)

Falls es im Datensatz fehlende Werte gibt, kann die Berechnung durch einen zusätzlichen Parameter angepasst werden. Wenn dies nicht gemacht wird, würde die normale Funktion NA zurückliefern. Die Lösung für diese Situation ist das Argument na.rm = TRUE, sodass die fehlenden Werte in der Berechnung einfach übersprungen werden: 

data_with_na <- c(4, 7, NA, 10, 6, NA, 9) 

median_na <-median(data_with_na, na.rm = TRUE) 

print(median_na)

Medianberechnung in SQL

In SQL gibt es keine direkte Funktion, welche für die Medianberechnung einer Spalte verwendet werden kann. Eine einfache Alternative wäre es deshalb, den Datensatz mithilfe von Pandas in einen DataFrame zu laden und dort die Berechnung fortzusetzen. Wenn dies keine Möglichkeit darstellt und man in SQL bleiben muss, so kann man den Median indirekt ermitteln, indem man den mittleren Wert aus einer geordneten Liste auswählt. 

Angenommen wir haben eine einfache Tabelle sales eines Unternehmens und darin die Spalte amount in der die verkaufte Menge abgelegt ist. Mithilfe der folgenden Abfrage können wir für einen Datensatz mit einer ungeraden Größe die entsprechende Zeile in der Tabelle ausgeben, die den Median enthält. 

WITH ordered AS (

    SELECT amount, 

           ROW_NUMBER() OVER (ORDER BY amount) AS row_num,

           COUNT(*) OVER () AS total_rows

    FROM sales

)

SELECT amount AS median

FROM ordered

WHERE row_num = (total_rows + 1) / 2;

Hierbei sind: 

• ROW NUMBER() OVER (ORDER BY amount) AS row_num: Dieser Ausdruck nummiert die Zeilen des Datensatzes, der vorher aufsteigend nach amount sortiert wurde. 
• COUNT(*) OVER () AS total_rows: In diesem Abschnitt wird die Größe des Datensatzes in der Variablen total_rows abgelegt. 
• Die WHERE Klausel stellt sicher, dass bei einer ungeraden Größe des Datensatzes genau das mittlere Element. Angenommen wir haben eine Datensatzgröße von 5, dann filtert die WHERE Klausel die Zeilen mit der Nummer (5+1)/2 = 3.

Bei einer geraden Datensatzgröße muss die Abfrage hingegen etwas abgeändert werden, sodass der Mittelwert der beiden mittleren Elemente berechnet wird. Somit gibt es dann eine neue WHERE Klausel: 

WITH ordered AS (

    SELECT amount, 

           ROW_NUMBER() OVER (ORDER BY amount) AS row_num,

           COUNT(*) OVER () AS total_rows

    FROM sales

)

SELECT AVG(amount) AS median

FROM ordered

WHERE row_num = (total_rows) / 2 

   OR row_num = (total_rows + 1) / 2;

Wie wir gesehen haben, ist die Median-Berechnung in verschiedenen Softwaresystemen möglich. Bei der Arbeit mit größeren Datensätzen sollte jedoch der Einfachheit halber auf Programmiersprachen, wie R oder Python, zurückgegriffen werden. Diese bieten dann auch zusätzlich die Möglichkeit, dass direkt weitere Datenanalyseschritte möglich sind. 

Welche Anwendungen nutzen den Median?

Der Median ist ein zentraler Lageparameter in der Statistik, der in vielen Anwendungen genutzt und vor allem dann sinnvoll ist, wenn Daten asymmetrisch verteilt sind oder Ausreißer enthalten. Doch außerhalb der Statistik ergeben sich auch viele andere Anwendungsgebiete: 

• Wirtschaft & Finanzen: Für die realistische Darstellung von Löhnen, Mieten oder Preisen ist der Median essenziel, um eine belastbare Aussage über die Mitte treffen zu können. So zeichnet beispielsweise die Medianmiete in einer Stadt ein realistisches Bild über die Wohnkosten der BürgerInnen, ohne dass es von sehr günstigen oder sehr teuren Wohnungen verzerrt wird. 
• Machine Learning: Vor allem in der Bildverarbeitung dient der Median als Filter zur Rauschreduzierung, um plötzliche und fehlerhafte Pixel gekonnt ersetzen zu können. Außerdem können Datensätze mithilfe dieser Kennzahl bearbeitet werden, um fehlerhafte Werte auszugleichen und mithilfe eines mittleren Wertes für dieses Attribut zu ersetzen. 
• Medizin & Biostatistik: Im Bereich der Krankenhausplanung ist es sinnvoll, die Medianaufenthaltsdauer von PatientInnen zu berechnen, um die Logistik dahinter, wie Personal, Krankenzimmer oder Verpflegung, entsprechend planen und sicherstellen zu können. Bei einer Durchschnittsbetrachtung hingegen könnten diese Zahlen aufgrund von Ausreißern zu niedrig oder zu hoch angesetzt werden. 
• Sozialwissenschaften: Im Bereich der Sozialwissenschaften wird der Median innerhalb der Demografie Forschung eingesetzt und beispielsweise das Medianalter der Bevölkerung bestimmt. 

Der Median als Kennzahl ist aus vielen Analysebereichen nicht mehr wegzudenken und wird vor allem genutzt, um den Einfluss von Ausreißern zu verringern. Vor allem in den Bereichen Wirtschaft, Machine Learning, Medizin und Sozialwissenschaften spielt er eine zentrale Rolle. 

Welche Erweiterungen des Medians gibt es?

Der Median ist zwar bereits eine sehr einfacher Lageparameter, welcher in verschiedensten Anwendungen genutzt werden kann. Jedoch gibt es spezielle Fälle, in denen der klassische Median nicht ausreicht, weshalb auf individuelle Erweiterungen zurückgegriffen werden muss. In diesem Abschnitt stellen wir einige der wichtigsten Erweiterungen kurz vor. 

Gleitender Median für die Zeitreihenanalyse

In der Zeitreihenanalyse werden häufig sogenannte Moving Averages betrachtet, also der Durchschnitt aus einem zurückliegenden Zeitraum, wie zum Beispiel die letzten fünf Tage oder drei Monate. Diese können jedoch extreme Werte in diesen Zeiträumen stark verzerrt werden, weshalb man auch auf den gleitenden Median zurückgreifen kann, der dahingehend robuster ist. Der Wert für den aktuellen Tag wird dann einfach berechnet, indem die Werte aus einem zurückliegenden Zeitraum verwendet werden und daraus mit der bekannten Definition der Median berechnet wird. 

Der gleitende Median wird beispielsweise bei den Bewertungen von Aktienkursen eingesetzt, um einen generellen Trend erkennen zu können, der nicht zu stark durch Ausreißer beeinflusst wird. In der Medizin hingegen hilft er bei Herzfrequenzsensoren, da diese kurzzeitigen Messfehlern oder Störungen unterliegen können. Durch die Nutzung des gleitenden Medians kann das tatsächliche Signal herausgefiltert und analysiert werden. 

Multidimensionaler Median für Vektordaten

Bisher haben wir nur den Median in einer Dimension betrachtet. Jedoch gibt es verschiedene Anwendungen, wie zum Beispiel die Bildverarbeitung oder Machine Learning im Allgemeinen, welche mit mehrdimensionalen Daten arbeiten, die in Vektoren vorliegen. Dafür wird dann der multidimensionale Median genutzt, welcher in jeder Dimension den eindimensionalen Median berechnet und anschließend aus den Werten einen entsprechenden Vektor erstellt. 

In der Bildverarbeitung kann dieses Vorgehen hilfreich sein, um zufälliges Rauschen aus Bildern zu entfernen und wird deshalb als sogenannter Medianfilter in der Vorverarbeitung von Bildern eingesetzt. Dort kann es zu einem sogenannten Impulsrauschen kommen, wenn digitale Bilder aufgrund einer Beschädigung zufällige helle und dunkle Pixel enthalten. Mithilfe dieses Filters werden dann die beschädigten Pixel durch die Mitte der umliegenden Pixel ersetzt. 

Im Machine Learning wird der mehrdimensionale Median darüber hinaus zum Beispiel beim k-Means Clustering eingesetzt. Dieser Algorithmus zielt darauf ab, die Elemente eines Datensatzes verschiedenen Cluster zuzuordnen. Dazu werden iterativ verschiedene Clusterzuordnungen getestet und in jedem Schritt ein Clusterzentrum gebildet, das die Mitte eines Clusters darstellt. Für diese Berechnung wird dann der mehrdimensionale Median genutzt.  

Geographischer Median für die Standortanalyse

Der geographische Median beschreibt den Punkt, der die kürzeste Gesamtentfernung zu allen anderen Punkten im Datensatz besitzt. Dazu werden für jeden Punkt die Distanz zu den allen restlichen Punkten berechnet und aufsummiert und anschließend das Element gewählt, welches die kürzeste Gesamtsumme aufweist. 

Diese Vorgehensweise kommt zum Beispiel in der Geschäftsplanung zum Einsatz, wenn verschiedene Standorte für ein Logistikzentrum bewertet werden oder wenn ein neuer Krankenhausstandort bestimmt werden soll. Außerdem kann er in der Netzwerkanalyse genutzt werden, um den optimalen Standort für einen neuen Mobilfunkmasten zu finden. 

Durch diese Erweiterungen wird der Median zu einem flexiblen und leistungsstarken Werkzeug, das in vielen standardisierten Anwendungen genutzt und darüber hinaus auch für speziellere Datenanalysen individualisiert werden kann. 

Das solltest Du mitnehmen

• Der Median ist eine grundlegende Kennzahl, welche eine Aussage über die zentrale Tendenz des Datensatzes liefert. 
• Er bestimmt einen Wert, welcher genau in der Mitte der Datenreihe ist und dadurch im Vergleich zum Mittelwert nicht so stark von Ausreißern beeinflusst wird. 
• Neben dem Median kann auch der Mittelwert oder der Modus genutzt werden, um die zentrale Tendenz eines Datensatzes zu bestimmen. 
• Der Median hat auch Nachteile, wie beispielsweise, dass Informationen über die Abstände der Datenpunkte verloren gehen. 
• Es gibt verschiedene Computerprogramme, welche zur Berechnung dieser Kennzahl genutzt werden können, wie zum Beispiel die Programmiersprache Python oder Excel.  

Andere Beiträge zum Thema Median

Dieser Link führt Dich zu meiner Deepnote-App, in der Du den gesamten Code findest, den ich in diesem Artikel verwendet habe, und ihn selbst ausführen kannst.