The Softmax is a mathematical function that is used primarily in the field of Machine Learning to convert a vector of numbers into a vector of probabilities. Especially in neural networks, it serves as a so-called activation function of the individual layers.

What is an Activation Function?

The activation function occurs in the neurons of a neural network and is applied to the weighted sum of input values of the neuron. Because the activation function is non-linear, the perceptron can also learn non-linear correlations.

Thus, the neural networks get the property to learn and map complex relationships. Without the non-linear function, only linear dependencies between the weighted input values and the output values could be created. Then, however, one could also use linear regression. The processes within a perceptron are briefly described in the following.

The perceptron has several inputs at which it receives numerical information, i.e. numerical values. Depending on the application, the number of inputs may differ. The inputs have different weights that indicate how influential the inputs are to the eventual output. During the learning process, the weights are changed to produce the best possible results.

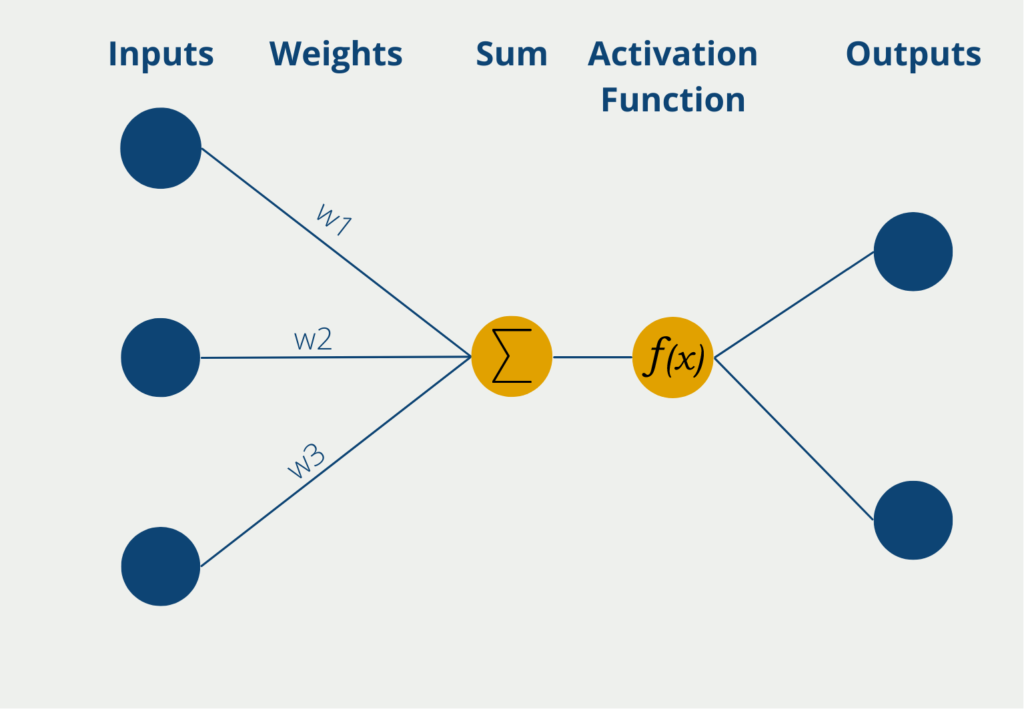
The neuron itself then forms the sum of the input values multiplied by the weights of the inputs. This weighted sum is passed on to the so-called activation function. In the simplest form of a neuron, there are exactly two outputs, so only binary outputs can be predicted, for example, “Yes” or “No” or “Active” or “Inactive”, etc.

If the neuron has binary output values, an activation function is used whose values also lie between 0 and 1. Thus, the output values result directly from the use of the function.

What is the Softmax-Function?

The softmax is a mathematical function that takes a vector as input and converts its individual values into probabilities, depending on their size. A high numerical value leads to a high probability in the resulting vector.

In words, each value of the vector is divided by the sum of all values of the initial vector and stored in the new vector. In purely mathematical terms, this formula then looks like this:

\(\) \[\sigma (x)_{j} = \frac{e^{z_{j}}}{\sum_{k=1}^{K} e^{z_{k}}} \text{for } j = 1, …, K.\]

With a concrete example, the operation of the Softmax function becomes clearer:

\(\) \[\begin{pmatrix}1 \\ 2 \\3 \end{pmatrix} \underrightarrow{Softmax} \begin{pmatrix}\frac{1}{1 + 2 + 3} \\ \frac{2}{1 + 2 + 3} \\ \frac{3}{1 + 2 + 3} \end{pmatrix} = \begin{pmatrix} 0.166 \\ 0.33 \\ 0.5 \end{pmatrix} \]

The positive feature of this function is that it ensures that the sum of the output values is always less than or equal to 1. This is very advantageous especially in the probability calculation because it is guaranteed that no added probability can come out greater than 1.

What are the activation functions?

There are many different activation functions that are used in Machine Learning. Among the most common are:

• Sigmoid function: This function maps the input values to the range between 0 and 1.
• Tanh function: The Tanh function, or tangent – hyperbolic for short, maps the input values to the range between -1 and 1.
• ReLU function: The Rectified Linear Unit, or ReLu function for short, takes the input value only if it is greater than or equal to zero. Otherwise, the output value is set to zero.
• Softmax function: The softmax function also maps the input values to the range between 0 and 1, but is particularly suitable for the last layer in the neural network to represent a probability distribution there.

What is the difference between Sigmoid and Softmax?

At first glance, the sigmoid and softmax functions appear relatively similar, since both functions map the input value to the numerical range between 0 and 1. Their course is also almost identical with the difference that the sigmoid function passes through the value 0.5 at x = 0 and the softmax function is still below 0.5 at this point.

The difference between the functions lies in the application. The sigmoid function can be used for binary classifications, i.e. for models in which a decision is to be made between two different classes. The softmax, on the other hand, can also be used for classifications that should predict more than two classes. In this case, the function ensures that the probability of all classes results in 1.

In fact, it can also be mathematically proven that in the case of two classes, the sigmoid and softmax functions coincide.

Which Machine Learning algorithms use Softmax?

As we have already learned, the softmax function is mainly used for multi-classification problems. The following models and algorithms make use of the function:

• Neural Networks: The last layer of the network has a softmax activation function when deciding between more than two classes.
• Reinforcement Learning: In reinforcement learning, the model often has to decide between several actions. The function is also used for this purpose.
• Logistic Regression: “Normal” logistic regression actually assumes two classes to be distinguished. With the help of the softmax function, it is also possible to build models that can classify more than two groups.

What are the limitations of the Softmax Function?

The softmax function is a powerful tool in probabilistic modeling and classification tasks. However, it also has certain limitations and considerations that should be taken into account:

1. Sensitivity to Outliers: The softmax function can be sensitive to outliers in the input data. Extreme values can have a significant impact on the resulting probabilities, potentially skewing the classification results.
2. Class Imbalance: It assumes that the classes are balanced, meaning that each class is represented equally in the training data. In situations where there is a significant class imbalance, the softmax function may struggle to assign appropriate probabilities to the minority classes.
3. Lack of Robustness to Overlapping Classes: If the decision boundaries between classes are not well-defined and classes overlap in feature space, the softmax function may have difficulty accurately assigning probabilities to the different classes.
4. Inability to Capture Uncertainty: The function produces confident probabilities for each class, even if the model’s confidence in its predictions is low. It does not explicitly capture uncertainty or ambiguity in the classification task.
5. Input Scaling: The softmax function is sensitive to the scale of the input values. If the input values are not properly scaled, it can affect the relative magnitudes of the resulting probabilities and potentially impact the classification accuracy.
6. Lack of Interpretable Probabilities: While softmax probabilities provide relative rankings among classes, they do not always represent the true probabilities in the real world. The probabilities may not be easily interpretable, especially when the model is trained on biased or limited data.
7. Alternative Decision Boundaries: Softmax assigns probabilities based on a decision boundary, and small changes in the input data can lead to different classifications. This means that the decision boundaries are not necessarily stable or unique.

It’s important to be aware of these limitations and consider them when using the softmax function in practice. Depending on the specific problem and requirements, alternative approaches like probabilistic classification methods or models that explicitly handle class imbalance and uncertainty may be more appropriate.

How to use the Softmax Function in Python?

In Python, the softmax function is commonly implemented using the NumPy library. NumPy provides efficient mathematical operations on arrays, which makes it suitable for computing the function for multiple classes. Here is an example of how the softmax function can be implemented in Python:

In this implementation, the input x is assumed to be a 2D array where each row represents a sample, and each column represents the score or logit for a specific class. The function calculates the exponential of each element x to obtain the numerator of the softmax equation. Then, the exponential values are summed along the appropriate axis (axis=1) to calculate the denominator. Finally, the probabilities are obtained by dividing each element of the numerator by the denominator.

The implementation utilizes the broadcasting feature of NumPy to perform element-wise operations efficiently across arrays. This allows the softmax function to be applied to multiple samples simultaneously.

It’s worth noting that the implementation provided here assumes a standard softmax function that operates on logits or scores. If you’re working with large values or need to handle numerical stability issues, you may consider applying additional techniques like subtracting the maximum value from each row of x before exponentiating (x - np.max(x, axis=1, keepdims=True)) to prevent overflow.

Additionally, TensorFlow provides its own implementation of the softmax function, which is particularly useful when working with neural networks and deep learning models.

To use it, you can leverage the built-in function tf.nn.softmax(). Here’s an example of how to use it:

In this example, the TensorFlow tf.nn.softmax() function is applied to the logits tensor, which represents the scores or logits for each class. The function computes the probabilities based on the input logits.

Using the TensorFlow implementation of softmax provides the advantage of seamlessly integrating with other TensorFlow operations and allowing the function to be used within neural network architectures. It also provides automatic differentiation for training deep learning models using techniques like backpropagation.

By combining the flexibility of TensorFlow with the softmax function, you can easily incorporate the calculations into your Machine Learning pipelines and take advantage of the extensive features and optimizations provided by TensorFlow.

This is what you should take with you

• The softmax function originates from mathematics and maps input values in the range [0, 1].
• It is very similar to the sigmoid function with the difference that for more than two classes, the probabilities add up to 1.
• Other activation functions are also used in machine learning, such as the tanh or the ReLU function.

Other Articles on the Topic of Softmax

Another interesting article about the Softmax activation function can be found here.