Die Dimensionsreduktion ist eine zentrale Methode im Bereich der Datenanalyse und des Machine Learnings, die es ermöglicht die Anzahl der Dimensionen in einem Datensatz zu verringern und dabei die enthaltenen Informationen möglichst zu erhalten. Dieser Schritt ist notwendig, um vor dem Training die Dimensionalität des Datensatzes zu verringern, um Rechenleistung zu sparen und dem Problem des Overfittings zu entgehen.

In diesem Beitrag beschäftigen wir uns im Detail mit der Dimensionsreduktion und deren Ziele. Außerdem veranschaulichen wir die am häufigsten verwendeten Methoden und beleuchten die Herausforderungen, welche die Dimensionsreduktion besitzt. 

Was ist die Dimensionsreduktion?

Die Dimensionsreduktion umfasst verschiedene Methoden, die das Ziel verfolgen die Zahl der Merkmale und Variablen in einem Datensatz zu verringern und dabei gleichzeitig die Informationen des Datensatzes zu erhalten. Es sollen also weniger Dimensionen eine vereinfachte Darstellung der Daten ermöglichen, ohne dabei Muster und Strukturen innerhalb der Daten zu verlieren. Dadurch können nachgeschaltete Analysen deutlich beschleunigt werden und außerdem Machine Learning Modelle optimiert werden. 

In vielen Anwendungen treten Probleme aufgrund der hohen Anzahl von Variablen in einem Datensatz auf, welches auch als Fluch der Dimensionalität bezeichnet wird, was wir im folgenden Abschnitt noch genauer beleuchten werden. Eine zu hohe Dimensionalität kann zum Beispiel zu diesen Problemen führen: 

• Overfitting: Wenn sich Machine Learning Modelle zu stark auf Charakteristiken des Trainingsdatensatzes einlassen und deshalb nur schlechte Ergebnisse für neue, ungesehene Daten liefern, spricht man von Overfitting. Bei einer hohen Anzahl von Merkmalen steigt das Risiko von Overfitting, da das Modell komplexer wird und sich deshalb zu stark an die Fehler des Datensatzes anpasst. 
• Rechenkomplexität: Analysen und Modelle, welche viele Variablen verarbeiten müssen, benötigen häufig auch mehr Parameter, die trainiert werden. Dadurch erhöht sich die Rechenkomplexität, was sich entweder in einer längeren Trainingszeit oder in einem erhöhten Ressourcenverbrauch widerspiegelt.
• Datenrauschen: Mit einer erhöhten Zahl von Variablen steigt auch die Wahrscheinlichkeit von fehlerhaften Daten oder sogenanntem Rauschen. Diese können die Analysen beeinflussen und zu fehlerhaften Vorhersagen führen. 

Obwohl große Datensätze mit vielen Merkmalen sehr informativ und wertvoll sind, kann die hohe Zahl an Dimensionen auch schnell zu Problemen führen. Die Dimensionsreduktion ist eine Methode, welche versucht den Informationsgehalt des Datensatzes zu wahren und trotzdem die Anzahl der Dimensionen zu verringern. 

Was ist der Fluch der Dimensionalität?

Der Curse of Dimensionality tritt bei hochdimensionalen Datensätzen auf, also solchen, die eine Vielzahl von Attributen oder Features haben. Im ersten Moment sind viele Attribute eine gute Sache, da sie viel Information enthalten und die Datenpunkte gut umschreiben. Wenn wir einen Datensatz über Personen haben, können die Attribute beispielsweise Informationen, wie die Haarfarbe, Größe, Gewicht, Augenfarbe etc. sein. 

Im mathematischen Sinne bedeutet jedes weitere Attribut jedoch eine neue Dimension im Raum und dadurch eine deutliche Erhöhung an Möglichkeiten. Dies wird anhand des folgenden Beispiels deutlich bei dem wir herausfinden wollen, welche Kunden welche Produkte kaufen. Im ersten Schritt betrachten wir dafür nur das Alter der Interessenten und ob sie das Produkt gekauft haben. Das können wir noch relativ einfach in einem zweidimensionalen Diagramm abbilden. 

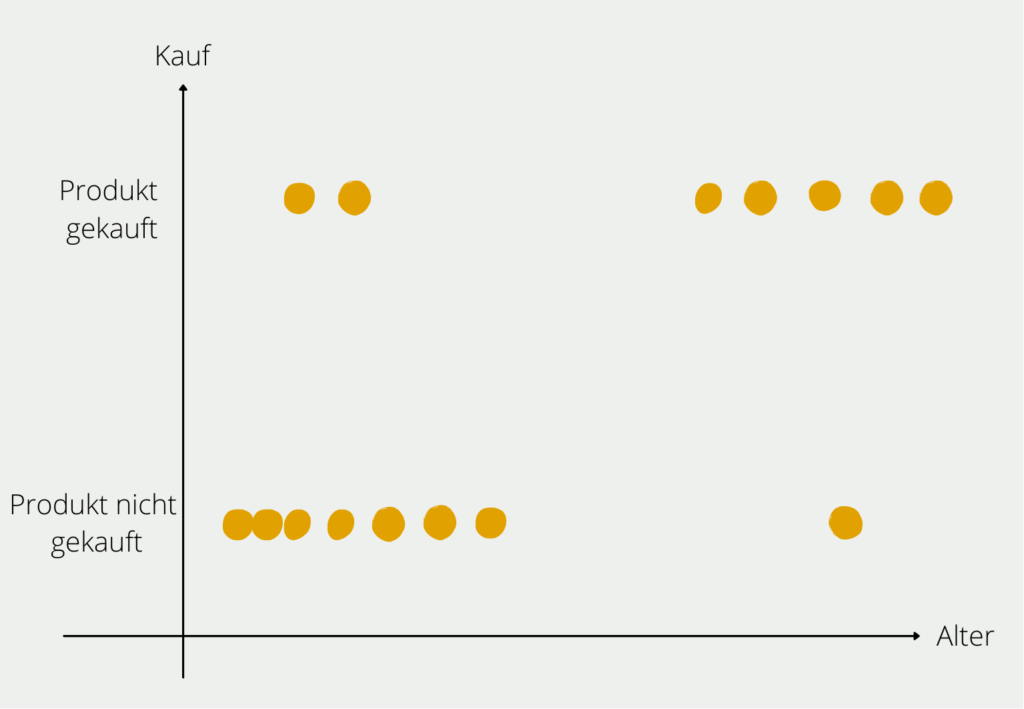
Sobald wir weitere Informationen zum Kunden hinzufügen, wird die Sache etwas komplexer. Die Information zu dem Einkommen des Kunden würde eine neue Achse bedeuten, auf der das numerische Einkommen abgebildet ist. Also wird aus dem zweidimensionalen Diagramm ein dreidimensionales. Das zusätzliche Attribut “Geschlecht” würde zu einer vierten Dimension führen und so weiter. 

In der Arbeit mit Daten ist es wünschenswert sehr viele Attribute und Informationen im Datensatz zu haben, um dem Modell viele Möglichkeiten zu lassen, Strukturen in den Daten zu erkennen. Jedoch kann es auch zu ernstzunehmenden Problemen führen, wie der Name Curse of Dimensionality bereits vermuten lässt. 

Data Sparsity

Das aufgezeigte Beispiel illustriert ein Problem, das mit vielen Attributen auftritt. Aufgrund der großen Anzahl der Dimensionen wächst auch der sogenannte Datenraum, das heißt die Zahl der Werte, die ein Datensatz annehmen kann. Dann kann es zu einer sogenannten Data Sparsity (deutsch: Datensparsamkeit) kommen. Das bedeutet, dass der Trainingsdatensatz zum Trainieren des Modells gewisse Ausprägungen gar nicht oder nur sehr selten enthält. Dadurch liefert das Modell für diese Randfälle auch nur schlechte Ergebnisse. 

Angenommen wir untersuchen in unserem Beispiel 1.000 Kunden, da es zu aufwändig wäre noch mehr Kunden zu befragen oder diese Daten einfach nicht zur Verfügung stehen. Möglicherweise sind bei diesen Kunden alle Altersklassen von jung bis alt gut vertreten. Wenn jedoch noch die weitere Dimension Einkommen hinzukommt, wird es schon unwahrscheinlicher, dass die möglichen Ausprägungen, wie beispielsweise “jung” und “hohes Einkommen” oder “alt” und “mittleres Einkommen”, vorkommen und mit genug Datenpunkten hinterlegt sind.

Distance Concentration

Wenn man im Machine Learning Bereich die Ähnlichkeit von verschiedenen Datensätzen bewerten will, werden dafür oft Distanzfunktionen genutzt. Die gängigsten Clustering-Algorithmen, wie beispielsweise das k-Means Clustering, setzen darauf, die Distanz zwischen Punkten zu berechnen und sie abhängig von der Größe einem Cluster zuzuordnen. In mehrdimensionalen Räumen kann es jedoch schnell zu dem Punkt kommen, dass alle Punkte ähnlich weit voneinander entfernt sind, sodass eine Trennung fast nicht möglich zu sein scheint. 

Dieses Phänomen kennen wir teilweise auch aus dem Alltag. Wenn man ein Foto schießt von zwei Objekten, wie beispielsweise zwei Bäumen, dann können diese auf dem Bild sehr nahe zueinander aussehen, da es lediglich ein zweidimensionales Bild ist. In echt kann es aber vorkommen, dass die Bäume mehrere Meter auseinander stehen, was erst in drei Dimensionen deutlich wird. 

Diese Problematiken, die im Zusammenhang mit vielen Dimensionen auftreten können, werden unter dem Begriff Curse of Dimensionality zusammengefasst.

Was sind die Ziele der Dimensionsreduktion?

Die Dimensionsreduktion verfolgt vor allem drei primäre Ziele: Verbesserung der Modellleistung, Visualisierung von Daten und die Erhöhung der Verarbeitungsgeschwindigkeit. Diese wollen wir in dem folgenden Abschnitt genauer beleuchten. 

Verbesserung der Modelleistung

Eines der Hauptziele der Dimensionsreduktion ist die Verbesserung der Modellleistung. Durch die Verringerung der Variablen in einem Datensatz kann ein weniger komplexes Modell verwendet werden, was wiederum das Risiko für Overfitting reduziert. 

Modelle, welche eine Großzahl von Parameter besitzen und dadurch eine hohe Komplexität haben, neigen dazu, sich zu sehr auf den Trainingsdatensatz und das darin enthaltene Rauschen der Daten anzupassen. Dadurch liefert das Modell bei neuen Daten, welche dieses Rauschen nicht aufweisen, schlechtere Ergebnisse, während die Genauigkeit beim Trainingsdatensatz hingegen sehr gut ist. Dieses Phänomen bezeichnet man als Overfitting. Bei der Dimensionsreduktion werden unwichtige oder redundante Merkmale aus dem Datensatz entfernt, wodurch das Risiko für eine Überanpassung sinkt. Dadurch liefert das Modell eine bessere Qualität bei neuen, ungesehenen Daten. 

Visualisierung von Daten

Wenn man Datensätze mit vielen Merkmalen visualisieren möchte, steht man vor der Herausforderung all diese Informationen in einem zwei- oder maximal dreidimensionalen Raum abzubilden. Jede Dimensionalität darüber hinaus ist für uns Menschen nicht mehr direkt greifbar, jedoch ist es am einfachsten jedem Merkmal im Datensatz eine eigene Dimension zuzuweisen. Deshalb steht man bei hochdimensionalen Datensätzen häufig vor dem Problem, dass man die Daten nicht einfach visualisieren kann, um so ein erstes Verständnis für die Eigenheiten der Daten zu bekommen und beispielsweise zu erkennen, ob es Ausreißer gibt.

Die Dimensionsreduktion hilft dabei die Anzahl der Dimensionen so weit zu verringern, dass eine Visualisierung im zwei- oder dreidimensionalen Raum möglich ist. Dadurch wird es einfacher, die Beziehungen zwischen den Variablen und die Datenstrukturen besser zu verstehen. 

Erhöhung der Verarbeitungsgeschwindigkeit

Insbesondere Machine Learning und Deep Learning Algorithmen spielt die Rechenzeit und die dafür notwendigen Ressourcen eine große Rolle bei der Umsetzung von Projekten. Häufig stehen nur begrenzte Ressourcen zur Verfügung, welche optimal genutzt werden sollen. Indem man frühzeitig redundaten Merkmale aus dem Datensatz entfernen kann, spart man nicht nur Zeit und Rechenleistung bei der Datenaufbereitung, sondern besonders auch beim Training des Modells, ohne dabei eine niedrigere Leistungsfähigkeit hinnehmen zu müssen. 

Zusätzlich ermöglicht die Dimensionsreduktion, dass möglicherweise einfachere Modelle verwendet werden können, die nicht nur während dem initialen Trainieren weniger Leistung benötigen, sondern auch später im Betrieb die Berechnungen schneller durchführen können. Dies ist vor allem bei Echtzeitberechnungen ein wichtiger Faktor. 

Insgesamt ist die Dimensionsreduktion eine wichtige Methode, um die Datenanalyse zu verbessern und robustere Machine Learning Modelle bauen zu können. Außerdem ist sie ein wichtiger Schritt bei der Visualisierung von Daten. 

Welche Methoden werden zur Dimensionsreduktion genutzt?

In der Praxis haben sich verschiedene Methoden zur Dimensionsreduktion durchgesetzt, von denen drei Stück im Folgenden genauer erläutert werden. Abhängig von der Anwendung und der Struktur der Daten bilden diese Methoden bereits ein breites Spektrum ab und können für die meisten praktischen Probleme genutzt werden.

Hauptkomponentenanalyse (Principal Component Analysis)

Die Hauptkomponentenanalyse geht davon aus, dass mehrere Variablen in einem Datensatz möglicherweise dasselbe messen, also korreliert sind. Diese verschiedenen Dimensionen können mathematisch zu sogenannten Hauptkomponenten zusammengefügt werden ohne, dass die Aussagekraft des Datensatzes darunter leidet. Die Schuhgröße und die Körpergröße beispielsweise sind häufig korreliert und können deshalb von einer gemeinsamen Dimension ersetzt werden, um die Zahl der Eingabevariablen zu verringern. 

Die Hauptkomponentenanalyse, oder englisch Principal Component Analysis (kurz: PCA), beschreibt ein Verfahren, wie diese Komponenten mathematisch berechnet werden kann. Die folgenden beiden Schlüsselkonzepte sind dabei zentral: 

Die Kovarianzmatrix ist eine Matrix, die die paarweisen Kovarianzen zwischen zwei verschiedenen Dimensionen des Datenraums angibt. Es handelt sich um eine quadratische Matrix, die also genauso viele Zeilen wie Spalten besitzt. Für zwei beliebige Dimensionen errechnet sich die Kovarianz wie folgt: 

\(\)\[ \text{Cov}\left(X, Y\right) = \frac{\sum_{i=1}^{n}\left(X_i – \bar{X}\right)\cdot\left(Y_i – \bar{Y}\right)}{n – 1} \]

Hierbei steht \(n\) für die Anzahl der Datenpunkte im Datensatz,  \(X_i\) ist der Wert der Dimension \(X\) des i-ten Datenpunkts und \(\bar{X}\) ist der Mittelwert der Dimension \(X\) für alle \(n\) – Datenpunkte. Die Kovarianzen zwischen zwei Dimensionen hängen, wie man an der Formel sehen kann, nicht von der Reihenfolge der Dimensionen ab, sodass gilt: \(COV(X,Y) = COV(Y,X)\). Aus diesen Werten ergibt sich die folgende Kovarianzmatrix \(C\) für die zwei Dimensionen \(X\) und \(Y\): 

\(\) \[C=\left[\begin{matrix}Cov(X,X)&Cov(X,Y)\\Cov(Y,X)&Cov(Y,Y)\\\end{matrix}\right]\]

Die Kovarianz aus zwei identischen Dimensionen ist dabei einfach die Varianz der Dimension selbst, also: 

\(\)\[C=\left[\begin{matrix}Var(X)&Cov(X,Y)\\Cov(Y,X)&Var(Y)\\\end{matrix}\right]\]

Die Kovarianzmatrix ist der erste wichtige Schritt in der Hauptkomponentenanalyse. Nachdem diese Matrix erstellt wurde, können daraus die Eigenwerte und Eigenvektoren berechnet werden. Mathematisch gesehen wird für die Eigenwerte die folgende Gleichung gelöst:

\(\)\[\det{\left(C-\ \lambda I\right)}=0\]

Hierbei ist \(\lambda\) der gesuchte Eigenwert und \(I\) die Einheitsmatrix in derselben Größe wie die Kovarianzmatrix \(C\). Wenn diese Gleichung gelöst wird, erhält man einen oder mehrere Eigenwerte einer Matrix. Sie stellen die lineare Transformation der Matrix in Richtung des zugehörigen Eigenvektors dar. Zu jedem Eigenwert kann also auch ein zugehöriger Eigenvektor berechnet werden, wofür die leicht abgewandelte Gleichung gelöst werden muss: 

\(\) \[\left(A-\ \lambda I\right)\cdot v=0\]

Wobei \(v\) der gesuchte Eigenvektor ist, nach dem die Gleichung entsprechend aufgelöst werden muss. Im Falle der Kovarianzmatrix entspricht der Eigenwert der Varianz des Eigenvektors, der wiederum eine Hauptkomponente darstellt. Jeder Eigenvektor ist also eine Mischung verschiedener Dimensionen des Datensatzes, die Hauptkomponenten. Der dazugehörige Eigenwert gibt also an, wie viel Varianz des Datensatzes durch den Eigenvektor erklärt wird. Umso höher dieser Wert, umso wichtiger ist die Hauptkomponente, da sie einen Großteil der Information des Datensatzes enthält. 

Deshalb werden nach Berechnung der Eigenwerte diese der Größe nach sortiert und die Eigenwerte mit den höchsten Werten werden ausgewählt. Anschließend werden die dazugehörigen Eigenvektoren berechnet und als Hauptkomponenten genutzt. Dadurch wird eine Dimensionsreduktion herbeigeführt, da statt der einzelnen Merkmale des Datensatzes nur die Hauptkomponenten zum Training des Modells genutzt werden. 

t-Distributed Stochastic Neighbor Embedding (t-SNE)

Das t-Distributed Stochastic Neighbor Embedding, kurz t-SNE, geht das Problem der Dimensionsreduktion anders an, indem es versucht einen neuen, niedrigdimensionalen Raum zu erschaffen, welcher die Abstände der Datenpunkte aus dem höherdimensionalen Raum möglichst übernimmt. Die Grundidee davon wird im folgenden Beispiel deutlich.

Es ist nicht einfach, Datensätze von einer hohen Dimensionalität in eine niedrige Dimensionalität zu überführen und dabei alle Informationen aus dem Datensatz möglichst zu erhalten. Die folgende Abbildung zeigt einen einfach, zweidimensionalen Datensatz mit insgesamt 50 Datenpunkten. Es lassen sich eindeutig drei verschiedene Cluster entdecken, die auch gut voneinander getrennt sind. Das gelbe Cluster ist am weitesten von den anderen beiden Clustern entfernt, während die lila und die blauen Datenpunkte näher zueinander sind. 

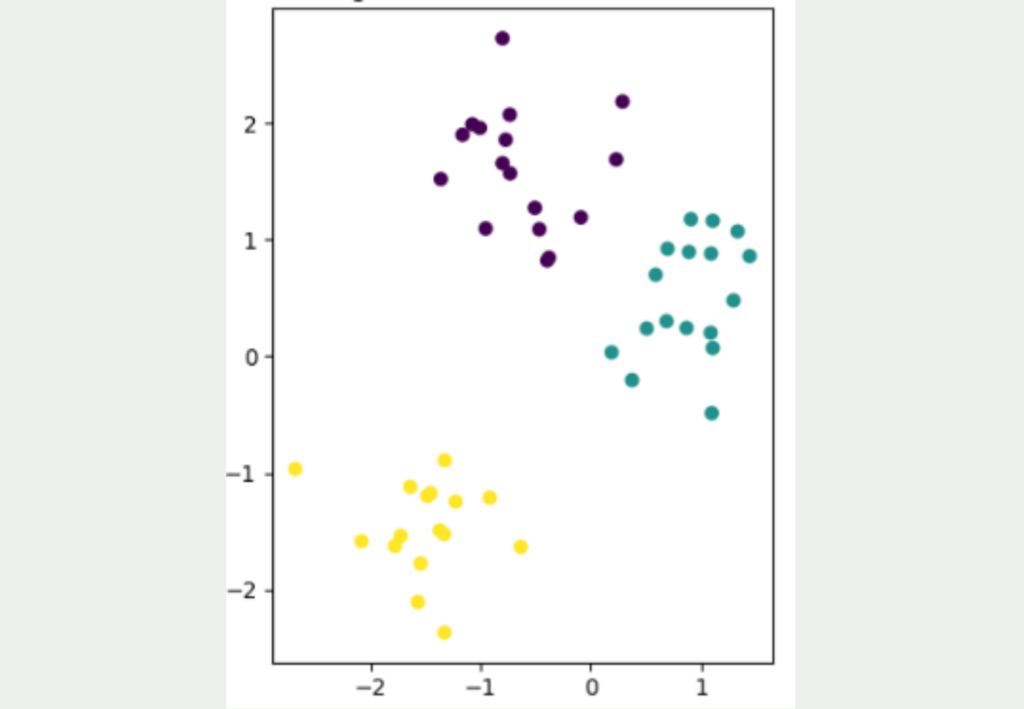
Das Ziel besteht nun darin, diesen zweidimensionalen Datensatz in eine niedrigere Dimension, also in eine Dimension, zu überführen. Der einfachste Ansatz hierfür wäre die Daten entweder nur durch ihre X- oder ihre Y-Koordinate zu repräsentieren. 

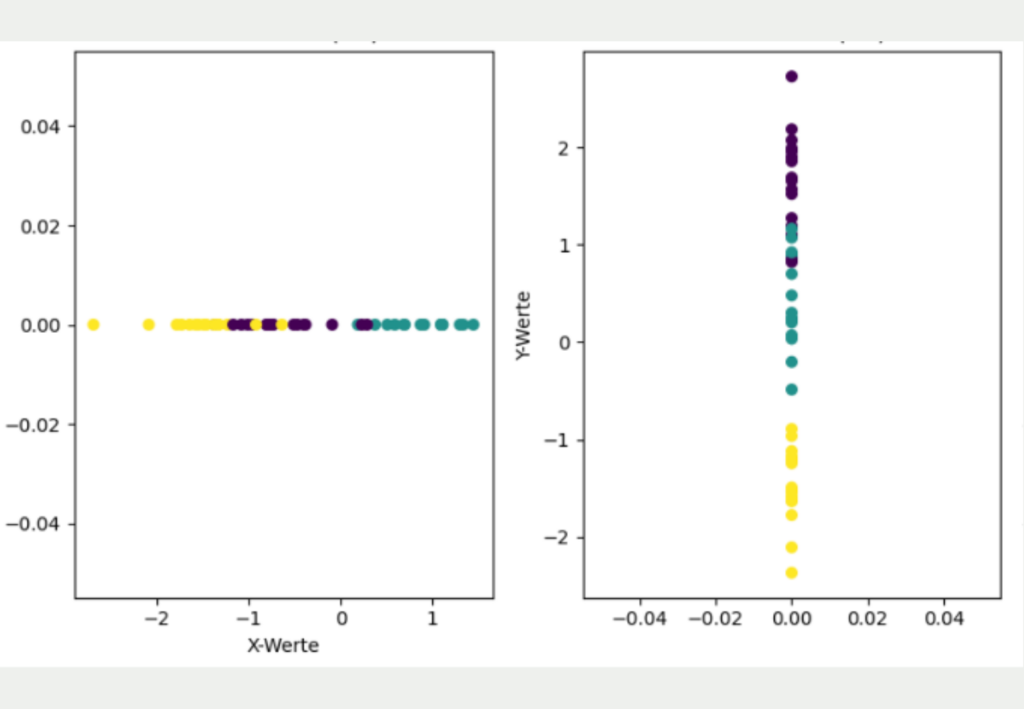
Jedoch wird deutlich, dass diese einfache Transformation einen Großteil der Informationen des Datensatzes verloren hat und ein anderes Bild vermittelt als die ursprünglich zweidimensionalen Daten. Wenn lediglich die X-Koordinaten genutzt werden, sieht es so aus, als würden sich das gelbe und das lila Cluster überlappen und als wären alle drei Cluster etwa gleichweit voneinander entfernt. Wenn hingegen nur die Y-Koordinaten für die Dimensionalitätsreduzierung genutzt werden, ist zwar das gelbe Cluster deutlich besser von den anderen Clustern getrennt, jedoch macht es dafür den Anschein, als würden sich das lila und blaue Cluster überlappen. 

Die Grundidee von t-SNE besteht darin, dass die Abstände aus der hohen Dimensionalität möglichst in die niedrige Dimensionalität mit übernommen werden. Dafür verwendet es einen stochastischen Ansatz und überführt die Abstände zwischen Punkte in eine Wahrscheinlichkeit, die angibt, wie wahrscheinlich es ist, dass zwei zufällige Punkte nebeneinander liegen. 

Genauer gesagt handelt es sich um eine bedingte Wahrscheinlichkeit, die angibt, wie wahrscheinlich es ist, dass ein Punkt den anderen Punkt als Nachbarn wählen würde. Daher auch der Name „Stochastic Neighbor Embedding“. 

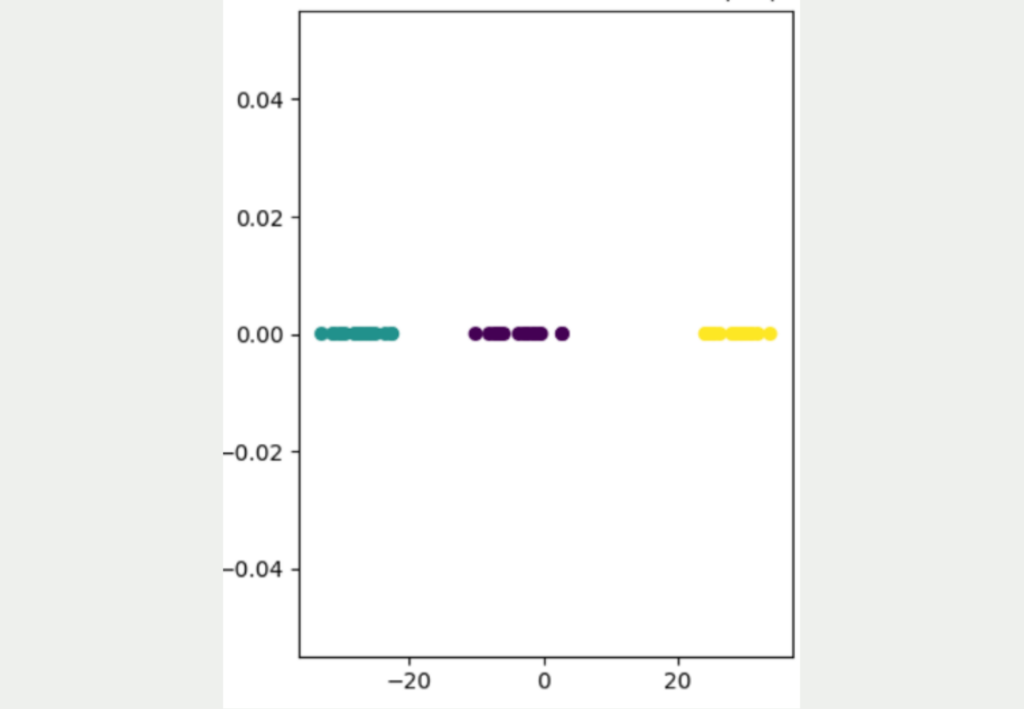
Wie man sehen kann, führt diese Herangehensweise zu einem deutlich besseren Ergebnis, in dem die drei verschiedenen Cluster deutlich voneinander unterschieden werden können. Außerdem wird deutlich, dass die gelben Datenpunkte deutlich weiter von den anderen Datenpunkten entfernt liegen und das blaue und lila Cluster etwas näher beieinander liegen. Um die Details dieser Herangehensweise besser zu verstehen, kannst Du dafür gerne unseren detaillierten Artikel zu diesem Thema lesen.

Linear Discriminant Analysis

Die Linear Discriminant Analysis (kurz: NDA) zielt darauf ab, die Trennbarkeit zwischen den Klassen zu erkennen und zu maximieren, indem sie die Daten auf eine geringere Dimension projiziert. Im Gegensatz zu anderen Methoden legt es vor allem Wert auf die Maximierung der Trennbarkeit zwischen den Klassen und ist deshalb besonders bei Klassifizierungsaufgaben von großer Bedeutung. 

Dabei werden zwei zentrale Kennzahlen berechnet: 

• Within-Class Scatter: Diese Kennzahl misst die Variabilität innerhalb einer Klasse von Daten. Umso geringer dieser Wert, umso ähnlicher sind die Datenpunkte innerhalb einer Klasse und umso klarer sind die Klassen getrennt.
• Between-Class Scatter: Diese Streuung wiederum misst die Variabilität zwischen den Mittelwerten der Klassen. Dieser Wert sollte möglichst groß sein, weil dies darauf hinweist, dass die Klassen besser voneinander trennbar sind. 

Einfach gesagt werden mithilfe von diesen Kennzahlen Matrizen gebildet und deren Eigenwerte berechnet, Die Eigenvektoren für die größten Eigenwerte wiederum sind die Dimensionen im neuen Merkmalsraum, welcher weniger Dimensionen aufweist als der ursprüngliche Datensatz. Anschließend können alle Datenpunkte auf die Eigenvektoren projiziert werden, wodurch die Dimensionen reduziert werden. 

Die Linear Discriminent Analysis bietet sich vor allem bei Anwendungen an, in welchen die Klassen bereits bekannt und die Daten auch klar gekennzeichnet sind. Es nutzt diese Klasseninformationen aus dem Supervised Learning, um einen niedrigdimensionalen Raum zu finden, welcher die Klassen möglichst gut trennt.

Ein Nachteil der LDA besteht darin, dass die maximale Reduktion auf einen Dimensionsraum begrenzt ist und von der Anzahl der Klassen abhängt. Ein Datensatz mit \(n\) Klassen kann dadurch maximal auf \(n-1\) Dimensionen reduziert werden. Konkret bedeutet dies beispielsweise, dass ein Datensatz mit drei unterschiedlichen Klassen auf einen zweidimensionalen Raum reduziert werden kann. 

Dieser Ansatz der Dimensionsreduktion bietet sich außerdem vor allem bei großen Datensätzen an, da der Rechenaufwand nur moderat ist und mit der Menge an Daten gut mitskaliert, sodass sich auch bei großen Datenmengen der Rechenaufwand in Grenzen hält.  

Welche Herausforderungen hat die Dimensionsreduktion?

Die Dimensionsreduktion stellt einen wichtigen Schritt in der Datenvorverarbeitung dar, um die Generalisierbarkeit von Machine Learning Modellen und die allgemeine Modellleistung zu erhöhen und möglicherweise Rechenleistung einzusparen. Jedoch bringen die Methoden auch einige Herausforderungen mit sich, welche vor der Nutzung beachtet werden sollten. Dazu gehören: 

• Informationsverlust: Obwohl die vorgestellten Methoden versuchen, so viel Varianz, also Informationsgehalt, des Datensatzes zu erhalten, geht bei der Reduzierung von Dimensionen gezwungenermaßen ein Teil der Informationen verloren. Dabei können auch wichtige Daten verloren gehen, welche möglicherweise zu schlechteren Analysen oder Modellergebnissen führen. Deshalb kann es passieren, dass das resultierende Modell weniger genau oder weniger leistungsfähig ist. 
• Interpretierbarkeit: Die meisten Algorithmen, welche zur Dimensionsreduktion verwendet werden, liefern einen niedrigdimensionalen Raum, welcher jedoch nicht mehr die ursprünglichen Dimensionen enthält, sondern eine mathematische Zusammenfassung daraus. Bei der Principal Component Analysis beispielsweise werden die Eigenvektoren genutzt, welche eine Zusammenfassung verschiedener Dimensionen aus dem Datensatz sind. Dadurch geht die Interpretierbarkeit zu einem gewissen Teil verloren, da die vorherigen Dimensionen einfacher zu messen und zu veranschaulichen sind. Besonders in Anwendungsfällen in denen Transparenz wichtig ist und die Ergebnisse eine praktische Interpretation benötigen, kann dies ein entscheidender Nachteil sein.
• Skalierung: Die Durchführung von Dimensionsreduktionen ist rechenintensiv und nimmt vor allem bei großen Datensätzen Zeit in Anspruch. Bei Echtzeitanwendungen ist diese Zeit jedoch nicht vorhanden, da die Rechenzeit des Modells noch hinzukommt. Vor allem rechenintensive Modelle, wie t-SNE oder Autoencoder, fallen dann schnell raus, da sie zu lange benötigen, um Livevorhersagen zu treffen. 
• Auswahl der Methode: Abhängig vom Anwendungsfall haben die vorgestellten Methoden der Dimensionsreduktion ihre Stärken und Schwächen. Deshalb spielt die Auswahl des geeigneten Algorithmus eine wichtige Rolle, da sie die Ergebnisse maßgeblich beeinflusst. Hierbei gibt es keine One-Size-Fits-All Lösung und es muss basierend auf der Anwendung immer eine neue Entscheidung getroffen werden. 

Die Dimensionsreduktion bringt viele Vorteile mit sich und ist in vielen Anwendungen ein fester Bestandteil der Datenvorverarbeitung. Jedoch müssen auch die genannten Nachteile und Herausforderungen beachtet werden, um ein leistungsfähiges Modell trainieren zu können. 

Das solltest Du mitnehmen

• Die Dimensionsreduktion ist eine Methode um die Anzahl der Dimensionen, also der Variablen, in einem Datensatz zu verringern und dabei möglichst den Informationsgehalt zu erhalten.
• Bei vielen Eingabevariablen ergibt sich der sogenannte Fluch der Dimensionalität. Dieser führt zu Problemen wie der Data Sparsity oder der Distance Concentration.
• Die Dimensionsreduktion führt häufig zu einer geringeren Wahrscheinlichkeit von Overfitting, einer besseren Visualisierbarkeit und optimierter Rechenleistung beim Training von Machine Learning Modellen.
• Zu den häufigsten Methoden der Dimensionsreduktion zählen die Hauptkomponentenanalyse, t-SNE und LDA.
• Die Dimensionsreduktion hat jedoch auch Nachteile, wie beispielsweise die schlechtere Interpretierbarkeit oder den Informationsverlust.

Andere Beiträge zum Thema Dimensionsreduktion

Praktische Beispiele für die Durchführung der Dimensionsreduktion in Scikit-Learn findest Du hier.