Wenn robuste Machine Learning Modelle trainiert werden sollen, benötigt man große Datensätze mit vielen Dimensionen, um ausreichend Strukturen zu erkennen und möglichst gute Vorhersagen zu liefern. Jedoch lassen sich solche hochdimensionalen Daten nur schwer visualisieren und verstehen. Deshalb benötigt man Verfahren zur Dimensionsreduktion, um komplexe Datenstrukturen zu visualisieren und eine Analyse betreiben zu können. 

Das t-Distributed Stochastic Neighbor Embedding (t-SNE/tSNE) ist ein Verfahren zur Dimensionsreduktion, das auf Abständen zwischen den Datenpunkten basiert und versucht diese Abstände in niedrigeren Dimensionen beizubehalten. Es ist eine Methode aus dem Bereich des Unsupervised Learnings und ist auch im Stande eine nicht-lineare Daten zu trennen, also Daten, die nicht durch eine Linie aufgeteilt werden, können. 

Warum benötigt man die Dimensionsreduktion?

Verschiedene Algorithmen, wie beispielsweise die Lineare Regression haben Probleme, wenn der Datensatz Variablen hat, die miteinander korreliert sind, also voneinander abhängen. Um dieser Problematik aus dem Weg zu gehen, kann es Sinn machen, die Variablen aus dem Datensatz zu entfernen, die mit einer anderen Variablen korrelieren. Gleichzeitig aber sollen die Daten auch nicht ihren ursprünglichen Informationsgehalt verlieren bzw. sollen so viel Information wie möglich behalten. 

Eine weitere Anwendung haben wir bei Clusteranalysen, wie beispielsweise dem k-Means Clustering, bei welchem wir die Anzahl der Cluster im Vorhinein definieren müssen. Die Dimensionalität des Datensatzes zu verringern hilft uns dabei, einen ersten Eindruck von den Informationen zu bekommen und beispielsweise abschätzen zu können, welches die wichtigsten Variablen sind und wie viele Cluster der Datensatz haben könnte. Wenn wir es beispielsweise schaffen, den Datensatz auf drei Dimensionen zu reduzieren, können wir die Datenpunkte in einem Diagramm visualisieren. Daraus lässt sich dann möglicherweise schon die Anzahl der Cluster ablesen.

Zusätzlich bieten große Datensätze mit vielen Variablen auch die Gefahr, dass das Modell overfitted. Das bedeutet einfach erklärt, dass das Modell sich im Training zu stark an die Trainingsdaten anpasst und dadurch nur schlechte Ergebnisse für neue, ungesehene Daten liefert. Daher kann es beispielsweise bei Neuronalen Netzwerken Sinn machen, das Modell erst mit den wichtigsten Variablen zu trainieren und dann Stück für Stück neue Variablen hinzuzunehmen, die möglicherweise die Performance des Modell weiter erhöhen ohne Overfitting.

Was sind die Grundprinzipien von t-SNE?

Das t-Distributed Stochastic Neighbor Embedding basiert auf einigen grundlegenden Konzepten, auf die im Folgenden genauer eingegangen wird, damit man die Grundzüge des Algorithmus verstehen kann: 

• Ähnlichkeitsmaß: Die Ähnlichkeit zwischen Datenpunkten werden mithilfe von Abstandsmaßen veranschaulicht, die messen, wie weit zwei Punkte voneinander entfernt liegen. Dafür wird typischerweise der euklidische Abstand genutzt, bei dem die Differenz zwischen den Koordinaten zweier Punkte in allen Dimensionen gebildet wird. Anschließend werden diese Differenzen jeweils quadriert und aufsummiert. Neben der Abstandsberechnung können auch andere Ähnlichkeitsmaße genutzt werden, wie zum Beispiel die Cosinus Ähnlichkeit. Dabei entscheidet der Winkel, den zwei Vektoren aufspannen, darüber wie ähnlich sie sind. Umso kleiner der eingeschlossene Winkel, umso ähnlicher die Datenpunkte. 
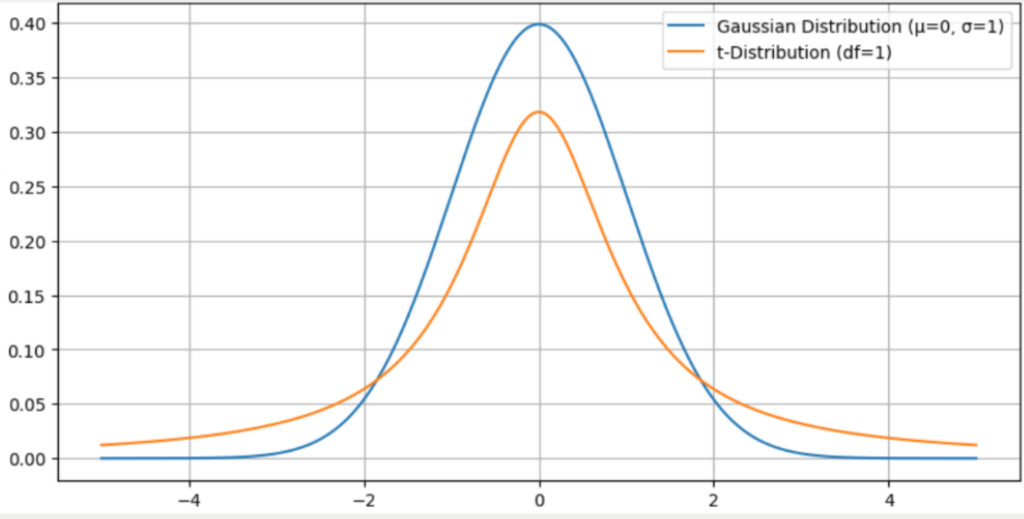
• Wahrscheinlichkeitsverteilung: Das t-SNE nutzt zwei Wahrscheinlichkeitsverteilungen. Im hochdimensionalen Raum wird versucht, alle Datenpunkte auf einer Gauss’schen Normalverteilung zu platzieren. Dabei wird ein Datenpunkt in der Mitte der Glockenkurve positioniert und die restlichen Punkte des Datensatzes anhand ihrer Distanz zu diesem Punkt auf der Gauss’schen Normalverteilung platziert. Umso näher ein Punkt zu dem gewählten Datenpunkt, umso näher ist dieser Punkt zum Mittelpunkt der Glockenkurve. Im niedrigdimensionalen Raum hingegen wird die t-Verteilung genutzt, die ähnlich ist zur Normalverteilung mit dem Unterschied, dass die Ränder etwas höher liegen und dadurch der Mittelpunkt etwas niedriger gelegen ist. Das Ziel des t-SNE Algorithmus ist es nun, einen Weg zu finden, wie die Gauss’sche Verteilung im hochdimensionalen Raum in eine t-Verteilung im niedrigdimensionalen Raum überführt werden kann und möglichst wenig Information dabei verloren geht.

• Embedding – Funktion: Zum Abschluss des Algorithmus wird eine Embedding-Funktion erstellt, die es ermöglicht, Datenpunkte im hochdimensionalen Raum auf Punkte im niedrigdimensionalen Raum zu mappen. Dabei wird jedem Punkt im hochdimensionalen Raum genau ein Punkt im niedrigdimensionalen Raum zugeordnet. 

Diese Grundprinzipien bilden die Basis für ein gutes Verständnis des t-SNE Algorithmus. 

Was ist die Idee von t-SNE?

Es ist nicht einfach, Datensätze von einer hohen Dimensionalität in eine niedrige Dimensionalität zu überführen und dabei möglichst alle Informationen aus dem Datensatz zu erhalten. Die folgende Abbildung zeigt einen einfachen, zweidimensionalen Datensatz mit insgesamt 50 Datenpunkten. Es lassen sich eindeutig drei verschiedene Cluster entdecken, die auch gut voneinander getrennt sind. Das gelbe Cluster ist am weitesten von den anderen beiden Clustern entfernt, während die lila und die blauen Datenpunkte näher zueinander liegen. 

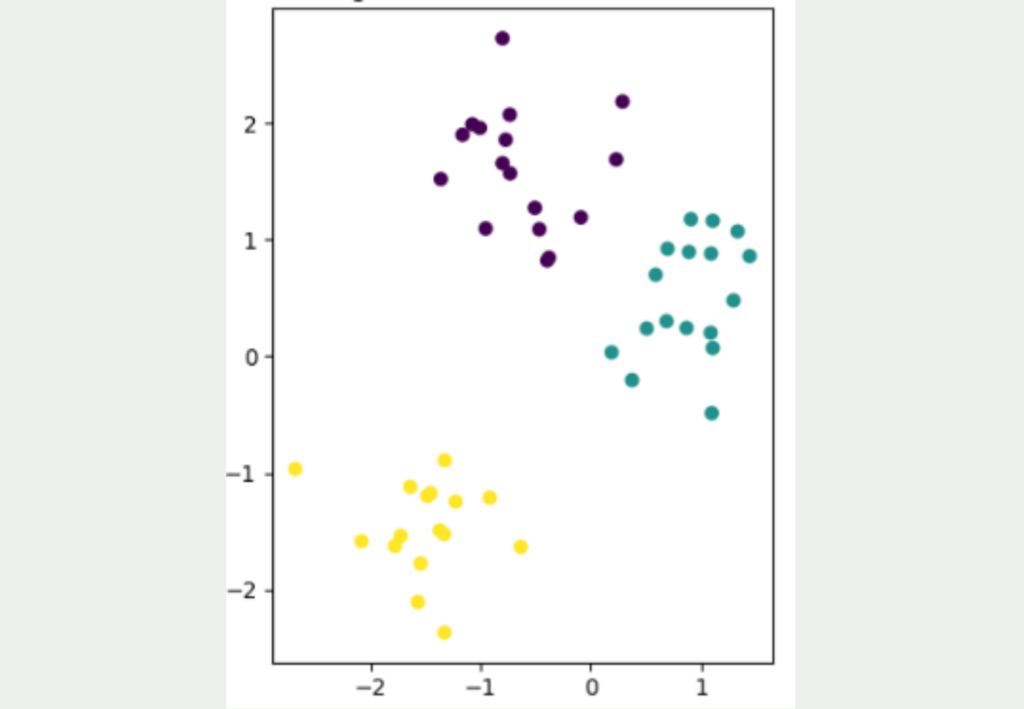
Das Ziel besteht nun darin, diesen zweidimensionalen Datensatz in eine niedrigere Dimension, also in eine Dimension, zu überführen. Der einfachste Ansatz hierfür wäre die Daten entweder nur durch ihre X- oder ihre Y-Koordinate zu repräsentieren. 

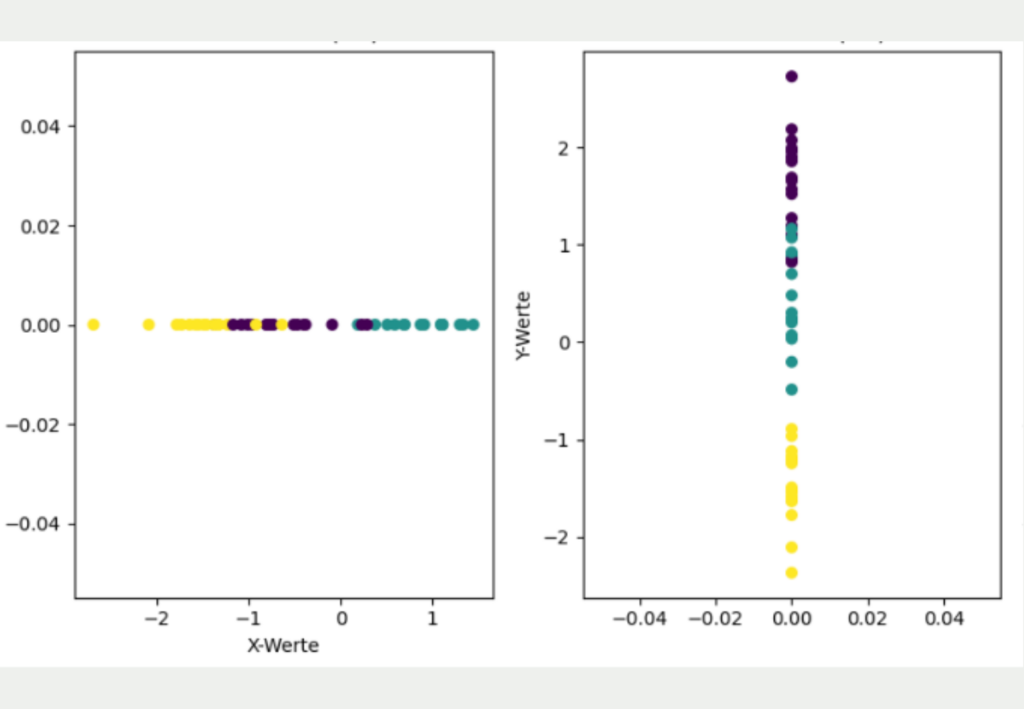
Jedoch wird deutlich, dass diese einfache Transformation einen Großteil der Informationen des Datensatzes verloren hat und ein anderes Bild vermittelt als die ursprünglich zweidimensionalen Daten. 

Wenn lediglich die X-Koordinaten genutzt werden, sieht es so aus, als würden sich das gelbe und das lila Cluster überlappen und als wären alle drei Cluster etwa gleichweit voneinander entfernt. Wenn hingegen nur die Y-Koordinaten für die Dimensionalitätsreduzierung genutzt werden, ist zwar das gelbe Cluster deutlich besser von den anderen Clustern getrennt, jedoch macht es dafür den Anschein, als würden sich das lila und blaue Cluster überlappen. 

Die Grundidee von t-SNE besteht darin, dass die Abstände aus der hohen Dimensionalität möglichst in die niedrige Dimensionalität mit übernommen werden. Dafür verwendet es einen stochastischen Ansatz und überführt die Abstände zwischen den Punkten in eine Wahrscheinlichkeit, die angibt, wie wahrscheinlich es ist, dass zwei zufällige Punkte nebeneinander liegen. 

Genauer gesagt handelt es sich um eine bedingte Wahrscheinlichkeit, die angibt, wie wahrscheinlich es ist, dass ein Punkt den anderen Punkt als Nachbarn wählen würde. Daher auch der Name „Stochastic Neighbor Embedding“. 

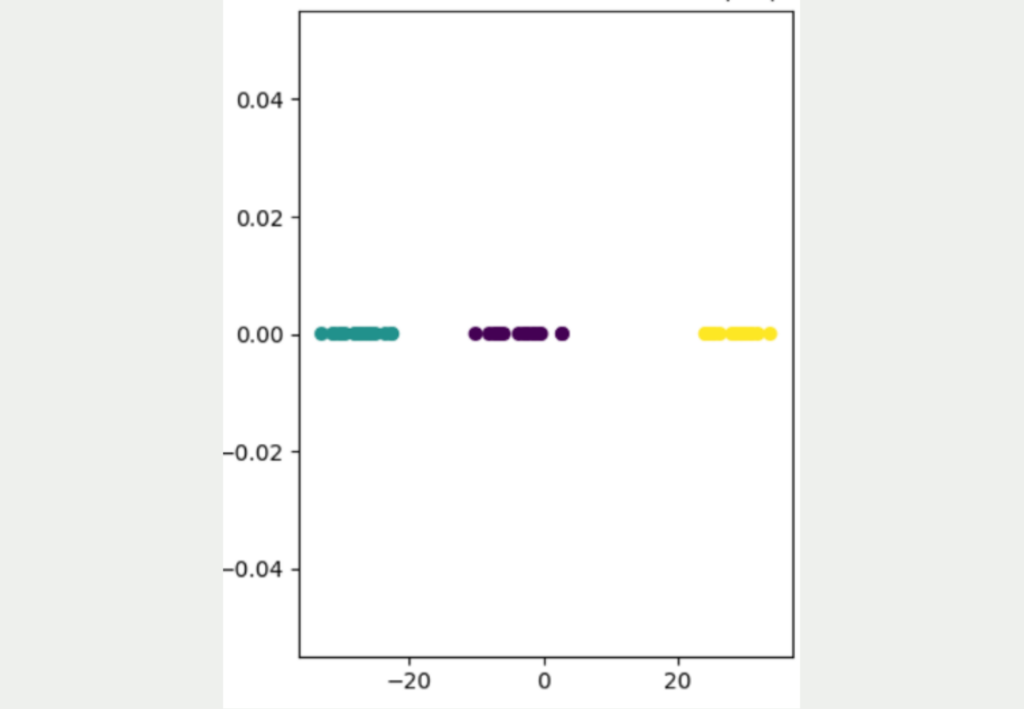
Wie man sehen kann, führt diese Herangehensweise zu einem deutlich besseren Ergebnis, in dem die drei verschiedenen Cluster deutlich voneinander unterschieden werden können. Außerdem wird deutlich, dass die gelben Datenpunkte deutlich weiter von den anderen Datenpunkten entfernt liegen und das blaue und lila Cluster etwas näher beieinander liegen. 

Wie funktioniert der t-SNE Algorithmus?

Im ersten Schritt berechnet der t-SNE Algorithmus eine Gauß’sche Wahrscheinlichkeitsverteilung für alle Punkte. Diese gibt an, wie wahrscheinlich es ist, dass zwei zufällig gewählte Punkte Nachbarn sind. Eine hohe Wahrscheinlichkeit zeigt an, dass die beiden Punkte nahe beieinander liegen, während eine niedrige Wahrscheinlichkeit auf einen großen Abstand zwischen den Punkten hinweisen. 

Für einen beliebigen gelben Datenpunkt könnte diese Verteilung wie in dem untenstehenden Diagramm aussehen. Die anderen gelben Datenpunkte liegen sehr nahe am gewählten Punkt und haben deshalb eine hohe Wahrscheinlichkeit ein Nachbar des gewählten Punktes zu sein. Die blauen und lila Punkte haben teilweise ähnliche Abstände und überschneiden sich deshalb. Jedoch sind sie alle deutlich unwahrscheinlicher ein Nachbar und liegen deshalb weiter außen auf der Normalverteilung.  

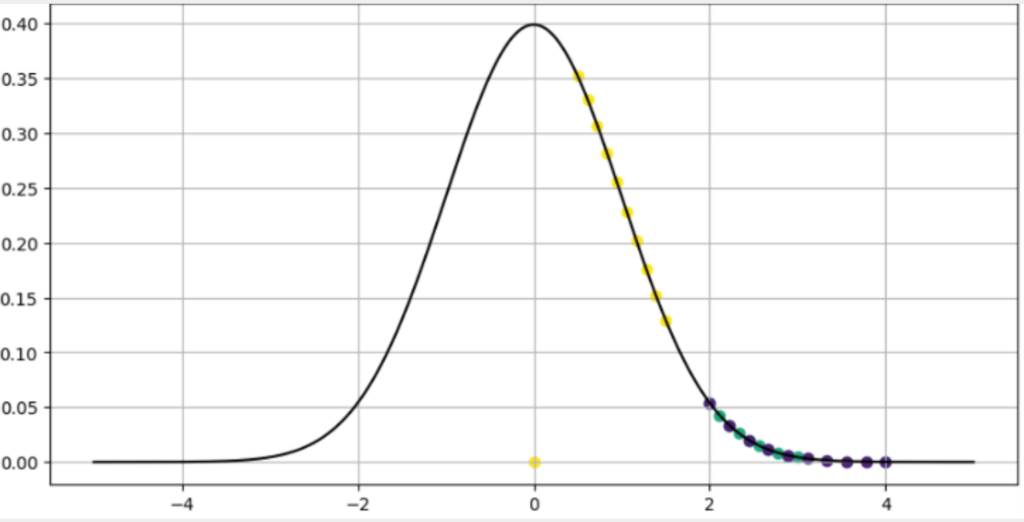
Im Paper, in dem t-SNE zum ersten Mal beschrieben wurde, ist außerdem festgelegt, dass die bedingte Wahrscheinlichkeit von einem Punkt zu sich selbst als Null definiert wird. Deshalb liegt ein Datenpunkt im Ursprung des Diagramms, da dieser Punkt nicht der Nachbar zu sich selbst sein kann.

Mathematisch gesehen wird diese Kurve als bedingte Wahrscheinlichkeit ausgedrückt, dass zwei Punkte \( x_j \) und \(x_i \) nebeneinander liegen. Dies ist der erste Teil von t-SNE nämlich das „Stochastic Neighbor Embedding“, wobei die Nachbarschaft von zwei Punkten mithilfe von Wahrscheinlichkeiten ausgedrückt werden kann. Diese Wahrscheinlichkeit kann mit der Formel berechnet werden: 

\(\) \[
p_{(j|i)} = \frac{\exp \left( – \frac{ \left\| x_i – x_j \right\|^2 }{ 2 \sigma_i^2 } \right)}{\sum_{k \neq l} \exp \left( – \frac{ \left\| x_k – x_l \right\|^2 }{ 2 \sigma_i^2 } \right)}
\]

Die einzelnen Parameter bedeuten im Detail: 

• \( p_{(j|i)}\): Dies stellt die Wahrscheinlichkeit dar, dass der Punkt  \(x_i \)den Punkt \( x_j \) als direkten Nachbarn im hochdimensionalen Raum wählen würde. 
•  \(x_i\) und \(x_j\) sind die beiden Datenpunkte im hochdimensionalen Raum. 
• \(\left\| x_i – x_j \right\| \) ist der Abstand zwischen den beiden Punkten. Hierfür wird häufig die euklidische Distanz genutzt, es kann jedoch jede gewünschte Abstandsmetrik genutzt werden. 
• \( \exp \left( – \frac{ \left\| x_i – x_j \right\|^2 }{ 2 \sigma_i^2 } \right) \) ist der komplexeste Teil dieser Formel und wird als die sogenannte Gauß’sche Kernelfunktion bezeichnet. Diese sorgt für die Glockenform der Kurve und bewirkt vor allem, dass aus Distanzen Wahrscheinlichkeiten zwischen 0 und 1 werden. Ansonsten wären die Werte der Distanzen auch immer abhängig von der Skala in der sich der Datensatz befindet. Die Standardabweichung des Punktes \( x_i \) hängt von der sogenannten Perplexität ab, die darüber bestimmt, ob sich das Modell eher auf die korrekte Abbildung von nahegelegenen Punkten oder auf Distanzen zwischen entfernten Punkten konzentrieren soll. Auf diesen Parameter wird im nächsten Abschnitt noch genauer eingegangen. 
• \( \sum_{k \neq l} \exp \left( – \frac{ \left\| x_k – x_l \right\|^2 }{ 2 \sigma_i^2 } \right) \) repräsentiert die Summe aller bedingten Wahrscheinlichkeiten zwischen dem Punkt \( x_l \) und allen anderen Datenpunkten im Datensatz außerdem dem Punkt \( x_l \) selbst. Es wird durch diesen Term geteilt, um sicherzustellen, dass die Summe aller bedingten Wahrscheinlichkeiten zwischen dem Punkt \( x_i \) und allen anderen Datenpunkten im Datensatz auf eins summiert. Ohne diesen Normalisierungsterm würde die Verteilung wie im vorangegangenen Diagramm aussehen. Das Problem hierbei ist jedoch, dass die Summe der Wahrscheinlichkeiten aller Datenpunkte größer 1 ist. Dieses Merkmal stellt sicher, dass eine interpretierbare Wahrscheinlichkeitsverteilung zustande kommt. 

Nachdem diese bedingte Wahrscheinlichkeit auf den hochdimensionalen Datenraum angepasst wurde, wird anschließend versucht sie in einen niedrigdimensionalen Datenraum zu überführen, sodass die bedingten Wahrscheinlichkeiten möglichst ähnlich bleiben. Bei dem herkömmlichen „Student Neighbor Embedding“ würde nun versucht werden, die bedingte Wahrscheinlichkeit in eine möglichst passende Gauß’sche Verteilung mit neuen Punkten im niedrigdimensionalen Raum zu überführen. Das „t“ in t-SNE steht jedoch für die sogenannte Students t-Distribution, die bereits im Abschnitt zu den Grundprinzipien genannt wurde. 

Die t-Verteilung zeichnet sich dadurch aus, dass sie bei Punkten, die weit vom Mittelwert entfernt liegen noch eine vergleichsweise hohe Wahrscheinlichkeit zuweist im Vergleich zur Gauß’schen Normalverteilung. Diese Eigenschaft der „Heavy Tails“ (deutsch: schwere Schwänze) ermöglicht es, dass im niedrigdimensionalen Raum auch Punkte, die weit vom untersuchten Punkt entfernt liegen noch ausreichend unterschieden werden können. 

Diese Eigenschaft wurde beim Stochastic Neighbor Embedding als sogenanntes Crowding Problem beschrieben. Es umschreibt den Fall, dass Punkte im niedrigdimensionalen Raum zu nahe beieinander liegen, insbesondere dann, wenn sie im hochdimensionalen Raum sehr weit vom untersuchten Punkt entfernt liegen. Durch die t-Distribution und deren „Heavy Tails“ wird dieses Problem behoben, da sie es ermöglicht, dass auch bei weit entfernten Punkten noch eine gewisse Separierung bestehen bleibt.

Die sogenannten Freiheitsgrade bei der t-Verteilung sind ein Parameter, der darüber bestimmt, wie viele unabhängige Stichproben genutzt werden, um eine Schätzung zu erstellen. Diese Freiheitsgrade haben auch einen erheblichen Einfluss auf die Verteilung, denn diese geben an, wie stark die Verteilung in die Breite gezogen werden. Umso mehr Freiheitsgrade, umso schmäler ist die Verteilung und umso mehr ähnelt sie der Normalverteilung. 

Für t-SNE wird ein Freiheitsgrad von eins gewählt, um die „Heavy Tails“ zu generieren und somit mehr Maße außerhalb des Zentrums, also des Mittelwerts zu haben. Niedrige Freiheitsgrade bedeuten also eine größere Wahrscheinlichkeit für Ausreißerdaten. Bei t-SNE ist diese Eigenschaft gewünscht, um die Punkt-zu-Punkt Beziehungen im niedrigdimensionalen Raum zu simulieren. Dadurch lässt sich eine Balance einrichten zwischen der Modellierung von nahen und weit entfernten Punkten. 

Somit muss die bedingte Wahrscheinlichkeit aus dem hochdimensionalen Raum auf eine t-Verteilung im niedrigdimensionalen Raum übertragen werden. Diese berechnet sich mithilfe der folgenden Formel: 

\(\) \[
q_{j|i} = \frac{(1 + \left\| y_i – y_j \right\|^2)^{-1}}{\sum_{k \neq l} (1 + \left\| y_k – y_l \right\|^2)^{-1}}
\]

Hierbei sind: 

• \(y_i \) und \(y_j \) sind zwei Datenpunkte im niedrigdimensionalen Raum, die die Punkte  aus dem hochdimensionalen Raum repräsentieren.
• \( q_{j|i} \) ist die bedingte Wahrscheinlichkeit, dass die Punkte \( y_i \) und \( y_j \) nahe beieinander liegen, also Nachbarn sind. 
• \( \left\| y_i – y_j \right\| \)ist der Abstand zwischen den beiden Punkten. Es sollte hier dieselbe Abstandsmetrik wie im hochdimensionalen Raum gewählt werden, also in den meisten Fällen der euklidische Abstand. 
• \( (1 + \left\| y_i – y_j \right\|^2)^{-1} \) repräsentiert die Ähnlichkeit zwischen zwei Punkten im niedrigdimensionalen Raum. Dafür wird die t-Verteilung mit einem Freiheitsgrad verwendet. 
• \( \sum_{k \neq l} (1 + \left\| y_k – y_l \right\|^2)^{-1} \) ist die Summe aller Wahrscheinlichkeiten zwischen zwei unterschiedlichen Punkten im Datensatz. Durch diese Summe wird geteilt, um eine Normalisierung herbeizuführen und sicherzustellen, dass die Wahrscheinlichkeiten sich auf eins summieren. 

Nun stellt sich die Frage, wie die vorhandene bedingte Wahrscheinlichkeit im hochdimensionalen Raum möglichst effektiv auf die bedingte Wahrscheinlichkeit im niedrigdimensionalen Raum übertragen werden kann. Dazu wird ein Optimierungsproblem definiert, das die sogenannte Kullback-Leibler (KL) Divergenz nutzt. Mithilfe des Gradientenverfahrens wird versucht die Divergenz zwischen den hochdimensionalen und den niedrigdimensionalen Wahrscheinlichkeiten zu minimieren. 

In diesem Artikel wird nicht weiter auf die mathematische Formulierung dieses Problem eingegangen, sondern lediglich der schematische Ablauf beschrieben. Die Optimierung ist ein iterativer Prozess, bei dem die Divergenz der beiden Wahrscheinlichkeiten berechnet und anschließend die Ableitung für einen einzelnen Punkt berechnet wird. Dieser Wert gibt an, wie stark das niedrigdimensionale Mapping eines Punktes verändert werden sollte. Das Vorzeichen bestimmt dabei die Richtung und der Wert die Stärke der Veränderung eines Punkts. Dadurch kann die Divergenz zwischen den beiden Wahrscheinlichkeiten verringert werden und das Ziel von t-SNE ist es, eine möglichst niedrige Divergenz zu erreichen, da dann die bedingte Wahrscheinlichkeit im hochdimensionalen und niedrigdimensionalen Raum möglichst ähnlich ist. 

Dieser iterative Prozess findet so lange statt, bis ein sogenanntes Konvergenzkriterium erreicht ist, also zum Beispiel eine maximale Zahl an Wiederholungen erreicht wurde oder die Divergenz zwischen den beiden Wahrscheinlichkeiten den vorgegebenen Wert unterschritten wurde. 

Was sind die Hyperparameter von t-SNE?

Der t-SNE Algorithmus hat einige Hyperparameter, die sowohl das Verhalten als auch die Leistung des Modells beeinflussen. In diesem Abschnitt werden die zentralen Hyperparameter vorgestellt und aufgezeigt, wie sich das Modell verändert, wenn diese Werte angepasst werden. 

Die Perplexität misst, wie viele Nachbarn während des Embedding Prozesses bei jedem Punkt berücksichtigt werden. Ein hoher Wert führt dazu, dass mehr Nachbarn mit einbezogen werden und dadurch auch die Abstände von weit entfernten Punkten besser in den niedrigen Dimensionen abgebildet werden. Bei einer niedrigen Perplexität hingegen liegt der Fokus eher darauf, die unmittelbare Nähe der Punkte möglichst akkurat abzubilden, auch wenn dafür die weit entfernten Punkte ungenauer abgebildet werden. 

Die Lernrate ist der zentrale Hyperparameter für das Gradientenverfahren, welches in schrittweisen Iterationen, die Embedding Positionen so verändert, dass die Divergenz zwischen den beiden Wahrscheinlichkeitsverteilungen möglichst gering ist. Die Lernrate bestimmt die Schrittgröße der einzelnen Updates der Embeddings. Bei einer hohen Lernrate können in einer Iteration große Veränderungen der Embeddings stattfinden, was auf der einen Seite zu einer schnelleren Konvergenz führen kann, auf der anderen Seite jedoch auch zu einem instabilen Lernprozess, da möglicherweise das optimale Ergebnis übersprungen wird und das Modell deswegen viel schwankt. Eine niedrige Lernrate hingegen führt dazu, dass wahrscheinlich mehr Iterationen benötigt werden, um zum Optimum zu gelangen, dafür jedoch das Training gleichmäßiger verläuft. 

Bevor man das Training starten kann, muss festgelegt werden, wann das Training gestoppt werden soll. Dazu kann entweder ein Schwellenwert für die Divergenz festgelegt werden, der zum Stopp führt, sobald er das erste Mal unterschritten wird, oder es wird eine maximale Zahl an Iterationen festgelegt. Diese Zahl bestimmt darüber, wie oft die Embedding Positionen optimiert werden können und kann bei vielen Anwendungen in die Hunderte oder Tausende gehen.

Die Zahl der Iterationen sollte abhängig von der Lernrate, der Daten und der Menge der zur Verfügung stehenden Ressourcen getroffen werden. Wenn es möglich ist, nutzt man am besten eine Kombination und definiert eine sogenannte Early Stopping Rule bei der das Modell entweder stoppt, wenn der Schwellenwert der Divergenz erreicht wurde oder die maximale Zahl an Iterationen erreicht ist. 

Das Ziel von t-SNE ist es einen hochdimensionalen Datensatz so zu transformieren, dass er mit deutlich weniger Dimensionen auskommt. Hierbei ist es meist das Ziel die Dimensionen des Embeddingraums auf zwei oder drei zu beschränken, damit sich die Daten visualisieren lassen und von menschlichen Nutzern interpretiert werden können. Hierbei bietet es sich an auf die dreidimensionale Einbettung zurückzugreifen, um dem Modell noch mehr Möglichkeiten zu geben, die ursprünglichen Informationen des Datensatzes abzubilden. Eine zweidimensionale Anordnung ist oft einfacher zu interpretieren, bietet aber auch einen niedrigeren Informationsgehalt. 

Ein weiterer Hyperparameter bei der Arbeit mit t-SNE ist das Abstandsmaß, welches genutzt wird. Standardmäßig wird die euklidische Distanz gewählt, welche die Differenzen zwischen allen Dimensionen zweier Punkte quadriert und anschließend aufsummiert. Diese Metrik ist nicht nur einfach zu berechnen, sondern bietet sich auch für viele Anwendungen als Ausgangspunkt an. In speziellen Fällen kann jedoch die Wahl von anderen Abstandsmetriken sinnvoll sein. Diese sind zum Beispiel: 

• Kosinusdistanz: Die sogenannte Kosinusähnlichkeit misst, wie ähnlich zwei Vektoren sind, indem der Winkel bestimmt wird, den die beiden Vektoren zueinander aufspannen. Die Kosinusdistanz errechnet sich, indem die Kosinusähnlichkeit von 1 abgezogen wird. Umso größer diese Distanz, umso verschiedener sind die beiden Vektoren. Diese Metrik bietet sich beispielsweise in der natürlichen Sprachverarbeitung an, wobei die Wörter durch Vektoren dargestellt werden. Dabei ist die Ähnlichkeit der Vektoren, also die Bedeutung der genutzten Wörter wichtiger als die Länge der Vektoren, welche die semantische Bedeutung der Wörter kodiert. 
• Manhattan-Distanz: Diese Abstandsmetrik wird auch Häuserblockdistanz genannt, da sie nicht den direkten Abstand zwischen Punkten berechnet, sondern die absolute Differenz in allen Dimensionen. Der Spitzname kommt daher, da sie sich verhält, wie ein Taxifahrer in Manhattan, der den Straßen folgen muss und somit von Block zu Block fährt. Diese Abstandsmetrik sollte genutzt werden, wenn die Merkmale in den Dimensionen nicht normalverteilt sind oder es Ausreißer im Datensatz gibt. 

Dies sind die wichtigsten Hyperparameter beim Training von t-SNE. Wie bei anderen Modellen auch, gibt es keine optimale Einstellung dieser Werte, die für alle Anwendungen und Datensätze geeignet ist. Vielmehr muss mit den Hyperparametern experimentiert werden, um das optimale Set an Werten zu finden und ein leistungsfähiges Modell trainieren zu können. 

Was sind die Grenzen von t-SNE?

t-SNE ist eine leistungsstarke Möglichkeit, um die Dimensionalität von Datensätzen zu verringern und trotzdem möglichst viele Informationen aus den ursprünglichen Daten zu behalten. Jedoch gibt es auch einige negative Aspekte, die vor der Nutzung beachtet werden sollten. 

Die Durchführung von t-SNE kann besonders bei großen Datensätzen sehr rechenintensiv sein und viel Zeit in Anspruch nehmen. Gerade die Optimierung der Verlustfunktionen benötigt viele Iterationen, bis sie bei einem aussagekräftigen Ergebnis angekommen ist. 

Der Algorithmus verwendet einige Hyperparameter, die einen großen Einfluss auf die Leistung des Modells haben und deshalb sorgfältig eingestellt werden müssen. Die Auswahl geeigneter Werte erfordert häufig verschiedene Tests, die Zeit und Rechenressourcen in Anspruch nehmen. 

Die Verlustfunktion bei t-SNE hat die mathematische Eigenschaft, dass sie nicht konvex ist. Dies bedeutet, dass der Graph mehrere sogenannte lokale Minima und nur ein einzigartiges, globales Minimum aufweist. Ein lokales Minimum zeichnet sich dadurch aus, dass es der niedrigste Punkt in einem gewissen Bereich ist, aber nicht der absolut niedrigste Punkt des Graphen im kompletten Definitionsbereich. Während der Optimierung der Verlustfunktion wird versucht einen Zustand zu erreichen, bei dem Divergenz zwischen den Wahrscheinlichkeitsverteilungen möglichst gering ist.

Abhängig von der Größe der Lernrate kann es nun passieren, dass der Algorithmus ein lokales Minimum erreicht und sich daraus nicht wegbewegt, da sich der Verlust in alle möglichen Schritte der Lernrate nur erhöht. Dadurch wird dem Algorithmus vorgetäuscht, dass er sich in einem optimalen Zustand befindet, in dem der Verlust minimal ist. Jedoch handelt es sich nicht um die bestmögliche Konfiguration, sondern eben lediglich um ein lokales Minimum. 

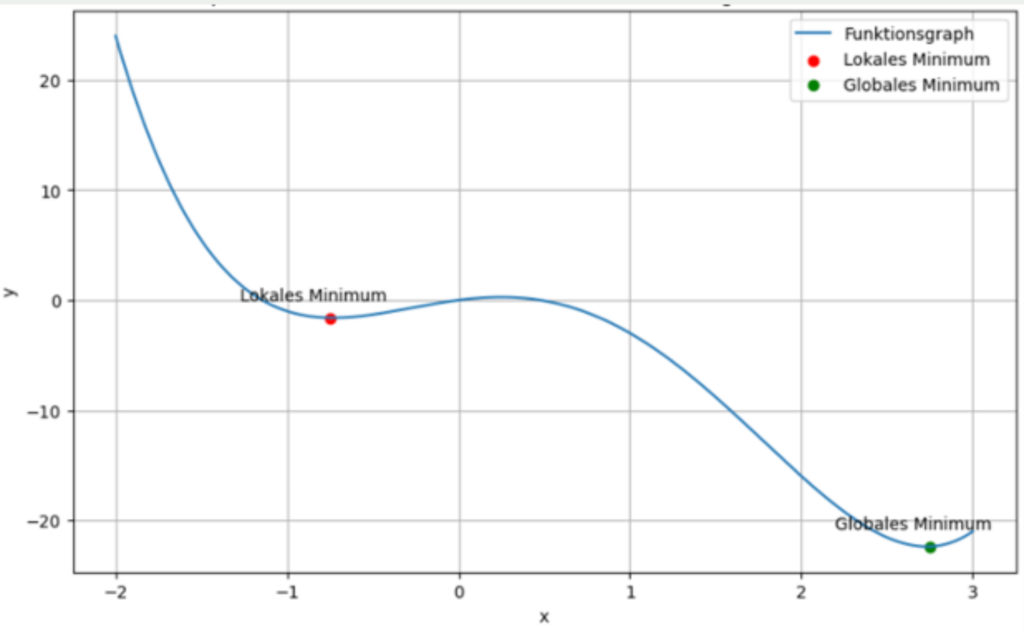
Ein weiterer Nachteil von t-SNE ist, dass der Algorithmus keine allgemeine Embedding-Funktion erlernt, die sich auch auf neue Datenpunkte anwenden lässt. Die Wahrscheinlichkeitsverteilung ist lediglich für den aktuellen Datensatz gültig und lässt sich nicht auf neue Punkte verallgemeinern. Wenn sich somit der Datensatz vergrößert, muss eine neue Wahrscheinlichkeitsverteilung errechnet werden. 

Hinzu kommt, dass t-SNE nicht-deterministisch ist, sodass mehrere Trainingsdurchläufe mit denselben Hyperparametern zu unterschiedlichen Ergebnissen führen können. Dies hängt mit der Nutzung der Wahrscheinlichkeitsverteilungen zusammen. Mehrere Durchläufe werden zwar zu ähnlichen, aber meist nicht zu exakt identischen, Ergebnissen führen. 

Ein weiterer wichtiger Nachteil von t-SNE ist, dass globale Strukturen und Abstände oft verloren gehen und sich hauptsächlich auf lokale Strukturen fokussiert wird. Dadurch können die globalen Zusammenhänge falsch interpretiert werden, weshalb t-SNE auch lediglich als Visualisierungshilfe für hochdimensionale Daten dienen sollte und nicht zum Clustern von Daten, da es zu falschen Ergebnissen führen kann. Dabei ist es auch oft missverständlich, dass die Daten nach der Anwendung von t-SNE so erscheinen, als würden sie perfekte Cluster bilden, obwohl dies in der Realität nicht unbedingt der Fall ist und meist auf den Umstand zurückzuführen ist, dass die globalen Strukturen nicht optimal abgebildet werden und der Fokus auf den direkten Nachbarn liegt. 

t-SNE vs. PCA

t-SNE und PCA sind zwei zentrale Techniken zur Dimensionsreduktion, die sehr weit verbreitet sind und in verschiedensten Analysen genutzt werden, um die Dimensionalität zu reduzieren und hochdimensionale Daten zu visualisieren. Es gibt jedoch einige grundlegende Unterschiede zwischen den beiden Methoden, die bei der Auswahl beachtet werden sollten. 

Bei PCA handelt es sich um eine lineare Methode zur Dimensionsreduktion, die auf der Kovarianzmatrix beruht und deren Eigenwerte und Eigenvektoren nutzt, um eine niedrigdimensionale Darstellung des Datensatzes zu finden. Dabei werden die Eigenvektoren mit den höchsten Eigenwerten genutzt, um die Daten in einen Datenraum zu überführen und trotzdem die maximale Varianz des Datensatzes zu erhalten. 

t-SNE hingegen ist ein nicht-linearer Ansatz, der es zum Ziel hat, die Abstände zwischen Daten in einem niedrigdimensionalen Raum möglichst genau abzubilden. Dazu werden die bedingten Wahrscheinlichkeiten berechnet, dass zwei beliebige Punkte Nachbarn sind. Im niedrigdimensionalen Raum soll dann eine ähnliche Wahrscheinlichkeit hergestellt werden. Dazu wird schrittweise die Kullback-Leibler Divergenz zwischen beiden Verteilungen minimiert. 

Aus diesen unterschiedlichen Architekturen ergeben sich auch einige Unterschiede: 

• Linearität: Wie beschrieben, handelt es sich bei PCA um eine lineare Methodik, sodass lediglich lineare Zusammenhänge zwischen den Datenpunkten erfasst werden können. Dies kann häufig nicht ausreichend sein, um die Komplexität des Datensatzes zu erfassen. Bei t-SNE hingegen handelt es sich um eine nicht-lineare Methode, die auch komplexere Zusammenhänge zwischen den Daten erfassen kann. 
• Interpretierbarkeit: Die Hauptkomponentenanalyse liefert häufig eine bessere Interpretierbarkeit, da die einzelnen Komponenten eine lineare Zusammenfassung der ursprünglichen Merkmale ist und außerdem bestimmt werden kann, welches Merkmal wie stark zu der Hauptkomponenten beiträgt. Bei t-SNE haben die niedrigen Dimensionen hingegen keine direkte Bedeutung in Bezug auf die Ausgangsdimensionen und lassen sich nicht so einfach interpretieren. Deshalb werden oft weitere Analysen benötigt, um die tatsächliche Bedeutung der niedrigen Dimensionen zu verstehen. 
• Rechenzeit: Vor allem bei großen Datensätzen mit vielen Dimensionen spielt es eine wichtige Rolle, wie gut sich die Methode skalieren lässt und wie viel Rechenzeit sie in Anspruch nimmt. Dabei schneidet PCA häufig besser ab als t-SNE, da es eine lineare Methode ist und deshalb effizientere Methoden verwendet werden können. Die Rechenzeit von t-SNE hingegen ist deutlich komplizierter vorherzusagen, da es sich um eine komplexe, iterative Optimierung handelt, bei der es schwierig ist, die Zeit vorherzusagen bis das Ergebnis konvergiert. Wenn die Datensätze größer werden, wird die Rechenzeit auch entsprechend höher, da iterative Verfahren, wie beispielsweise das Gradientenverfahren, deutlich komplexer werden.  
• Hyperparameter: Die Hauptkomponentenanalyse erfordert keinerlei Hyperparameter und liefert somit immer dieselben Ergebnisse für den gleichen Datensatz. Bei t-SNE hingegen gibt es verschiedene Hyperparameter, wie die Perplexität oder die Lernrate, die einen entscheidenden Einfluss auf das Ergebnis haben und deshalb sorgfältig abgestimmt werden sollten. Dieser Prozess erfordert besonders bei hochdimensionalen Datensätzen viel Zeit, da unterschiedliche Parameterkombinationen getestet und verglichen werden müssen. 
• Determinismus: In der Informatik bedeutet Determinismus, dass ein System für eine Eingabe immer dasselbe Ergebnis liefert, da immer derselbe Prozess mit denselben Zwischenergebnissen durchlaufen wird. Bei der Hauptkomponentenanalyse handelt es sich um einen deterministischen Prozess, da derselbe Datensatz immer dieselben Hauptkomponenten liefern wird. Bei t-SNE hingegen kann es in verschiedenen Durchläufen, selbst mit identischen Hyperparametern, zu unterschiedlichen Ergebnissen kommen, weshalb es ein stochastischer Prozess ist. Die Ursache dafür ist das Optimierungsverfahren, welches möglicherweise in lokalen Minima stecken bleibt und deshalb nicht immer das optimale Ergebnis findet. Somit bietet lediglich die Hauptkomponentenanalyse die Sicherheit, dass immer das optimale Ergebnis gefunden wird. 
• Umgang mit neuen Daten: Die Hauptkomponentenanalyse bietet die Möglichkeit, dass auch neue Datenpunkte in niedrigere Dimensionen überführt wird. Die entsprechenden Hauptkomponenten werden einmal auf einem Datensatz trainiert und können anschließend zur Umwandlung verwendet werden, da eine feste Regel existiert, wie hochdimensionale Punkte in niedrigdimensionale umgerechnet werden. Bei t-SNE hingegen ist das anders, da keine direkte Funktion vom hochdimensionalen in den niedrigdimensionalen Raum erlernt wird, sondern lediglich eine Wahrscheinlichkeitsverteilung. Diese kann nicht auf neue Datenpunkte angewandt werden, sondern es muss eine komplett neue Optimierung gestartet werden, um auch nur einen neuen Datenpunkt umzuwandeln. 
• Dimensionalität: Das Ziel von t-SNE ist es, die Abstände in einem hochdimensionalen Raum möglichst akkurat in niedrigere Dimensionen zu überführen. Dies scheitert häufig am sogenannten Crowding-Problem, welches beschreibt, dass Datenpunkte aus dem hochdimensionalen Raum im niedrigdimensionalen Raum sehr nahe zusammenfallen. Je mehr Dimensionen jedoch der niedrigdimensionale Raum hat desto weniger stark ist dieses Crowding-Problem. Deshalb ist t-SNE nur dann zur Dimensionsreduktion geeignet, wenn nur wenige Dimensionen, zum Beispiel zwei oder drei, vorhanden sind. In höheren Dimensionen kann es passieren, dass die Optimalität des Ergebnisses nicht gegeben ist. Die Ergebnisse der Hauptkomponentenanalyse hingegen sind unabhängig von der gewählten Dimensionalität, da stets versucht wird, die erklärte Varianz anhand der vorgegebenen Anzahl der Dimensionen zu maximieren. Somit ist die Qualität der Ergebnisse unabhängig von der Dimensionalität. 
• Anwendungen: Diese Unterschiede führen auch dazu, dass sich die Anwendungsgebiete und Einsatzbereiche der beiden Methoden unterscheiden. Die Hauptkomponentenanalyse wird häufig verwendet, um Datensätze langfristig in eine niedrigere Dimension zu überführen und auch neue Daten umwandeln zu können. Deshalb kommt es vor allem in der Merkmalsextraktion oder der Datenkompression zum Einsatz. Die t-SNE Methode hingegen dient in der explorativen Datenanalyse zur Visualisierung von großen Datensätzen, um ein Verständnis für die Informationen herzustellen und mögliche Muster zu erkennen. Jedoch dient es oft nicht zur konkreten Kompression von Daten. 

PCA und t-SNE sind zwei weit verbreitete und effektive Algorithmen im Bereich der Dimensionalitätsreduktion. Jedoch unterscheiden sie sich in verschiedenen Punkten, die bei der Auswahl der jeweiligen Methode beachtet werden sollten. Abschließend lässt sich sagen, dass t-SNE eine geeignete Methode ist, um hochdimensionale Datensätze zu visualisieren und mögliche Muster zu erkennen. PCA hingegen ist eine deterministische Alternative, die eine schnelle Dimensionsreduktion ermöglicht und außerdem eine reproduzierbare Möglichkeit bietet, neue Daten in einen niedrigdimensionalen Raum zu überführen. 

Wie kann t-SNE in Python implementiert werden?

Die Machine Learning Bibliothek Scikit-Learn in Python weist neben anderen Funktionalitäten auch eine Funktion auf, um in wenigen Schritten eine Dimensionalitätsreduzierung mithilfe von t-SNE durchführen zu können. Analog zum Beispiel mit der Principal Component Analysis wird hierfür auch der Auto-MPG Datensatz verwendet. 

Die nötigen Importe für dieses Beispiel umfassen Pandas für die Arbeit mit dem Datensatz, Scikit-Learn für die Skalierung der Daten und für die Dimensionsreduzierung mit t-SNE, sowie matplotlib damit die zweidimensionalen Daten anschließend auch visualisiert werden können.  

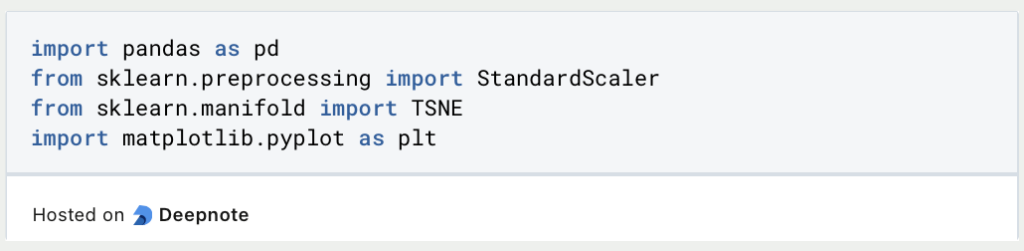
Der Datensatz wird aus einer CSV-Datei geladen und anschließend die kategorische Variable origin entfernt, da diese nicht so einfach von t-SNE verarbeitet werden kann. Außerdem wird die Angabe zu Miles per Gallon (MPG) entfernt, da diese nicht in die Reduzierung mit einfließen soll. t-SNE ist in vielen Fällen ein Vorverarbeitungsschritt für das Training eines Machine Learning Modells. Für dieses würde MPG als Zielvariable dienen und sollte deshalb nicht reduziert werden. 

Bevor der t-SNE Algorithmus auf die Daten angewandt wird, bietet es sich an, die Dimensionen auf einen einheitlichen Wert, zum Beispiel zwischen 0 und 1, zu skalieren. Dies ist zwar kein notwendiger Schritt, kann jedoch vorteilhafte Auswirkungen auf den Trainingsprozess haben, damit Dimensionen mit höheren Skalen in der Dimensionalitätsreduzierung nicht nur aufgrund der höheren Skala bevorzugt werden. Außerdem kann t-SNE mit skalierten Dimensionen auch schneller konvergieren. 

Es gibt viele Möglichkeiten, um den Datensatz zu skalieren. In diesem Beispiel wird der Standard Scaler verwendet. 

Anschließend wird die t-SNE Variable mit den Hyperparametern instanziiert. Hierbei wird die Anzahl der Komponenten bestimmt, also die Anzahl der Dimensionen, die das Resultat haben soll. Die Lernrate gibt an, wie groß die Schritte zwischen den Iterationen sein soll und die Perplexität bestimmt den Einfluss von nahen Punkten auf die Wahrscheinlichkeit im Vergleich zu weit entfernten Punkten. 

Die Resultate aus dem Trainingsprozess von t-SNE können nun in einem zweidimensionalen Diagramm veranschaulicht werden. Wichtig ist hierbei, dass die zwei Dimensionen nichts mehr mit den ursprünglichen Dimensionen zu tun haben und somit nicht direkt benannt werden können, da sie eine Mischung aus den vorher genutzten Dimensionen darstellen. 

Das solltest Du mitnehmen

• Das t-distributed stochastic neighbor embedding (kurz: tSNE) ist ein unsupervised Algorithmus zur Dimensionsreduktion in großen Datensätzen.
• Es wird benötigt, um Datensätze in der Dimension zu reduzieren und so mögliches Overfitting von Modellen zu verhindern.
• Der Hauptunterschied zur Principal Component Analysis ist, dass es auch für nicht-lineare Zusammenhänge zwischen den Datenpunkten verwendet werden kann. Diese Eigenschaft hat einen weitreichenden Einfluss zum Beispiel auf die Reproduzierbarkeit der Ergebnisse oder auf die benötigte Rechenzeit.
• In Python kann t-SNE zum Beispiel mit der Bibliothek Scikit-Learn umgesetzt werden.

Andere Beiträge zum Thema tSNE

• Scikit-Learn bietet eine ausführliche Dokumentation zur Nutzung von tSNE in Python.