Was ist Model Evaluation?

Die Model Evaluation ist ein entscheidender Schritt im Arbeitsablauf des maschinellen Lernens, bei dem die Leistung eines trainierten Modells anhand verschiedener Metriken und Techniken bewertet wird. Es muss sichergestellt werden, dass das Modell genau auf ungesehene Daten verallgemeinert werden kann und zuverlässige Vorhersagen liefert. In diesem Artikel werden wir die wichtigsten Konzepte und Techniken der Modellevaluierung untersuchen.

Warum ist Model Evaluation beim maschinellen Lernen wichtig?

Die Model Evaluation ist ein entscheidender Schritt beim maschinellen Lernen, da sie es uns ermöglicht, die Leistung unserer Modelle auf unbekannten Daten abzuschätzen. Die Evaluierung eines Modells anhand der Trainingsdaten kann zu einem Overfitting führen, bei der das Modell bei den Trainingsdaten gut, bei den Testdaten jedoch schlecht abschneidet. Daher hilft uns die Model Evaluation, das beste Modell auszuwählen und eine Überanpassung zu vermeiden, indem sie eine realistische Einschätzung der Leistung des Modells auf neuen Daten liefert. Sie hilft auch dabei, die Grenzen des Modells und verbesserungswürdige Bereiche zu ermitteln. Letztendlich ist eine gute Model Evaluation für die Entwicklung zuverlässiger und genauer Modelle für maschinelles Lernen erforderlich.

Welche Metriken werden zur Model Evaluation verwendet?

Bei der Bewertung der Leistung von Vorhersagemodellen werden verschiedene Bewertungsmetriken verwendet, um ihre Effektivität in verschiedenen Bereichen und Aufgaben zu messen. Das Verständnis dieser Bewertungsmetriken ist entscheidend für die effektive Bewertung und den Vergleich von Modellen. Hier sind einige gängige Bewertungsmetriken:

Genauigkeit: Die Genauigkeit ist eine weit verbreitete Metrik, die den Anteil der korrekt klassifizierten Instanzen an der Gesamtzahl der Instanzen misst. Sie liefert eine Gesamtbewertung der Modellleistung, kann aber bei einem Ungleichgewicht der Klassen irreführend sein.
Präzision: Die Präzision berechnet den Anteil der wahren Positiven (korrekt vorhergesagte positive Instanzen) an allen positiven Vorhersagen. Sie quantifiziert die Fähigkeit des Modells, falsch-positive Vorhersagen zu vermeiden, was besonders bei Anwendungen wichtig ist, bei denen falsch-positive Vorhersagen kostspielig sind.
Recall (Empfindlichkeit oder Rate der wahren Positiven): Die Rückrufquote misst den Anteil der vom Modell vorhergesagten richtig positiven Fälle an allen tatsächlich positiven Fällen. Sie gibt die Fähigkeit des Modells an, alle positiven Fälle zu identifizieren, und ist besonders wichtig, wenn die Folgen von falsch-negativen Ergebnissen schwerwiegend sind.
F1-Score: Der F1-Score kombiniert Präzision und Recall in einer einzigen Metrik. Er ist das harmonische Mittel aus Precision und Recall und bietet eine ausgewogene Bewertung der Leistung eines Modells. Der F1-Score ist geeignet, wenn Präzision und Recall gleichermaßen wichtig sind.
Spezifität: Die Spezifität misst den Anteil wahrer Negative (korrekt vorhergesagte negative Instanzen) an allen tatsächlich negativen Instanzen. Sie ist das Komplement der Falsch-Positiv-Rate und ist besonders bei binären Klassifikationsaufgaben von Bedeutung.
Fläche unter der Receiver Operating Characteristic Curve (AUC-ROC): Die AUC-ROC ist eine beliebte Metrik für die Model Evaluation von binären Klassifikatoren. Sie misst die Leistung bei verschiedenen Klassifizierungsschwellenwerten, indem sie die Rate der echten positiven Ergebnisse gegen die Rate der falschen positiven Ergebnisse aufträgt. Ein höherer AUC-ROC-Wert weist auf eine bessere Unterscheidungsfähigkeit des Modells hin.
Mean Squared Error (MSE): MSE ist eine bei Regressionsaufgaben häufig verwendete Metrik. Sie berechnet die durchschnittliche quadratische Differenz zwischen vorhergesagten und tatsächlichen Werten. Ein niedriger MSE weist auf eine bessere Modellleistung mit geringeren Fehlern hin.
Root Mean Squared Error (RMSE): Der RMSE ist die Quadratwurzel des MSE und liefert eine Metrik in den ursprünglichen Einheiten der Zielvariablen. Er ist besonders nützlich, wenn die Skala der Zielvariablen wichtig ist.
Mean Absolute Error (MAE): Der MAE berechnet die durchschnittliche absolute Differenz zwischen vorhergesagten und tatsächlichen Werten. Er liefert ein Maß für die durchschnittliche Größe der Fehler und ist im Vergleich zum MSE weniger empfindlich gegenüber Ausreißern.
R-Squared (Bestimmungskoeffizient): R-Quadrat misst den Anteil der Varianz in der abhängigen Variable, der durch die unabhängigen Variablen erklärt werden kann. Es reicht von 0 bis 1, wobei 1 eine perfekte Anpassung anzeigt. R-Quadrat wird häufig bei der linearen Regression verwendet, kann aber auch auf andere Modelle ausgedehnt werden.

Es ist wichtig zu beachten, dass die Wahl der Metriken für die Model Evaluation von dem spezifischen Problem, den Datenmerkmalen und den Anforderungen des Bereichs abhängt. Berücksichtige die Ziele der Aufgabe und wähle dementsprechend geeignete Metriken aus. Außerdem ist es ratsam, mehrere Metriken zu analysieren, um ein umfassendes Verständnis der Modellleistung zu erhalten.

Welche Techniken werden bei der Model Evaluation eingesetzt?

Die Model Evaluation umfasst eine Reihe von Techniken, die darauf abzielen, die Leistung und Qualität von Modellen des maschinellen Lernens zu bewerten. Diese Techniken liefern wertvolle Erkenntnisse darüber, wie gut sich ein Modell auf unbekannte Daten verallgemeinern lässt und wie gut es die ihm zugedachte Aufgabe erfüllt. Durch den Evaluierungsprozess gewinnen Praktiker ein Verständnis für die Stärken, Grenzen und die allgemeine Effektivität eines Modells. Mithilfe dieser Evaluierungstechniken können sie fundierte Entscheidungen über die Modellauswahl, Optimierung und mögliche Verbesserungen treffen, was zu zuverlässigeren und wirkungsvolleren Anwendungen des maschinellen Lernens in verschiedenen Bereichen führt.

Train-Test-Split

Im Bereich des maschinellen Lernens und der prädiktiven Modellierung ist es unerlässlich, die Leistung des Modells auf ungesehenen Daten zu bewerten, um seine Verallgemeinerbarkeit zu beurteilen. Der Train-Test-Split ist eine häufig angewandte Technik, die die Bewertung des Modells auf unabhängigen Datensätzen ermöglicht. Mit diesem Ansatz lässt sich abschätzen, wie gut das Modell auf neuen, unbekannten Daten funktionieren wird. So funktioniert die Aufteilung zwischen Training und Test:

Aufteilung des Datensatzes: Der erste Schritt beim Training-Test-Split ist die Aufteilung des verfügbaren Datensatzes in zwei verschiedene Teilmengen: den Trainingssatz und den Testsatz. Der Trainingsdatensatz wird zum Trainieren des Modells verwendet, während der Testdatensatz als unabhängiger Datensatz zur Bewertung der Leistung des trainierten Modells dient.
Datenzuweisung: Die Aufteilung der Daten auf den Trainingssatz und den Testsatz basiert in der Regel auf einem vordefinierten Verhältnis, z. B. 70:30, 80:20 oder 90:10. Der Trainingssatz enthält einen größeren Teil der Daten, so dass das Modell Muster und Beziehungen aus einer großen Menge von Informationen lernen kann. Der Testsatz hingegen ist relativ klein und wird getrennt gehalten, um reale Szenarien zu simulieren, in denen das Modell auf neue, ungesehene Daten stößt.
Trainieren des Modells: Mit der Trainingsmenge in der Hand wird das Modell mit verschiedenen Algorithmen und Techniken trainiert, je nach Art des Problems. Während der Trainingsphase lernt das Modell aus den Eingabedaten, optimiert seine Parameter und passt seine internen Darstellungen an, um Fehler zu minimieren oder die Leistung auf den Trainingsdaten zu maximieren.
Model Evaluation: Sobald das Modell trainiert ist, wird es anhand des Testsatzes bewertet. Der Testsatz enthält Instanzen, auf die das Modell während des Trainings nicht gestoßen ist. Durch die Bewertung der Leistung des Modells auf diesem unabhängigen Datensatz erhalten wir Einblicke in seine Fähigkeit, zu verallgemeinern und genaue Vorhersagen auf neuen, unbekannten Daten zu treffen.
Leistungsmetriken: In der Phase der Model Evaluation werden verschiedene Leistungskennzahlen (z. B. Genauigkeit, Präzision, Wiedererkennungswert, F1-Score oder andere, die für die jeweilige Aufgabe relevant sind) anhand der Vorhersagen des Modells für den Testsatz berechnet. Diese Metriken liefern eine objektive Bewertung der Leistung des Modells und dienen als Entscheidungshilfe für die Eignung des Modells für den Einsatz oder die weitere Verfeinerung.

Die Aufteilung in Trainings- und Testdaten ermöglicht eine faire Bewertung der Leistung eines Modells durch die Simulation realer Szenarien. Durch die Aufteilung des Datensatzes in Trainings- und Testdatensätze können potenzielle Probleme wie Overfitting (wenn ein Modell bei den Trainingsdaten außergewöhnlich gut, bei den ungesehenen Daten jedoch schlecht abschneidet) erkannt und die Leistung des Modells bei neuen Daten geschätzt werden.

Es muss unbedingt sichergestellt werden, dass die Aufteilung zwischen Trainings- und Testdaten repräsentativ für die zugrunde liegende Datenverteilung ist. Häufig werden Randomisierungstechniken eingesetzt, um zu verhindern, dass sich Verzerrungen oder Muster im ursprünglichen Datensatz auf die Trainings- oder Testdaten übertragen. Bei Aufgaben, die Zeitreihendaten oder abhängige Beobachtungen beinhalten, können außerdem spezielle Techniken wie die zeitliche Aufteilung oder die geschichtete Aufteilung eingesetzt werden, um die zeitlichen oder strukturellen Merkmale der Daten zu berücksichtigen.

Zusammenfassend lässt sich sagen, dass der Training-Test-Split eine grundlegende Technik der Model Evaluation ist, die eine Schätzung der Leistung eines Modells auf unabhängigen Daten ermöglicht. Indem das Modell auf einem Teil der Daten trainiert und auf einem anderen Teil evaluiert wird, liefert der Train-Test-Split Einblicke in die Verallgemeinerungsfähigkeiten des Modells und hilft, fundierte Entscheidungen über seinen Einsatz oder weitere Verbesserungen zu treffen.

Cross Validation

Die Kreuzvalidierung ist eine grundlegende Technik bei der Model Evaluation, die die Beschränkungen der traditionellen Trainings- und Testaufteilung ausgleicht. Sie bietet eine solidere Bewertung der Leistung eines Modells, indem die verfügbaren Daten in mehrere Teilmengen oder “Folds” unterteilt werden und das Modell iterativ an verschiedenen Kombinationen von Trainings- und Validierungsmengen bewertet wird. Die am häufigsten verwendete Kreuzvalidierungstechnik ist die k-fache Kreuzvalidierung, bei der die Daten in k gleich große Falten unterteilt werden.

Das Modell wird auf k-1 Falten trainiert und auf der verbleibenden Falte bewertet, wobei dieser Prozess k-mal wiederholt wird, um sicherzustellen, dass jede Falte sowohl als Trainings- als auch als Validierungssatz dient. Durch die Mittelung der über die k Iterationen erhaltenen Leistungsmetriken liefert die Kreuzvalidierung eine zuverlässigere Schätzung der Generalisierungsleistung des Modells.

Einer der Hauptvorteile der Kreuzvalidierung ist, dass sie eine umfassendere Bewertung der Leistung des Modells ermöglicht. Durch die Verwendung verschiedener Kombinationen von Trainings- und Validierungssätzen wird das Risiko einer Über- oder Unteranpassung verringert, was dazu beiträgt, die Fähigkeit des Modells zur Verallgemeinerung auf ungesehene Daten zu bewerten. Die Kreuzvalidierung ist besonders nützlich, wenn der Datensatz begrenzt ist, da sie die Nutzung der verfügbaren Daten maximiert. Sie gibt auch Aufschluss über die Stabilität der Leistung des Modells über verschiedene Teilmengen der Daten hinweg und hilft, potenzielle Probleme wie Datenempfindlichkeit oder -variabilität zu erkennen.

Es ist jedoch zu beachten, dass die Kreuzvalidierung rechnerisch aufwändiger ist als eine einfache Aufteilung in Training und Test, da sie mehrere Iterationen des Modelltrainings und der Bewertung erfordert. Der erhöhte Rechenaufwand kann die Durchführbarkeit in bestimmten Szenarien mit großen Datensätzen oder eingeschränkten Ressourcen einschränken. Darüber hinaus beseitigt die Kreuzvalidierung nicht alle Einschränkungen der Model Evaluation, wie etwa Datenverzerrungen oder externe Faktoren. Daher sollte sie in Verbindung mit anderen Bewertungstechniken und Überlegungen eingesetzt werden, um ein umfassenderes Verständnis der Modellleistung zu erhalten.

Zusammenfassend lässt sich sagen, dass die Kreuzvalidierung eine leistungsstarke Technik der Model Evaluation ist, die im Vergleich zu herkömmlichen Trainings- und Testaufteilungen eine robustere Schätzung der Leistung eines Modells liefert. Sie trägt dazu bei, das Risiko der Überanpassung zu mindern, nutzt die Daten effektiver und gibt Aufschluss über die Stabilität der Modellleistung. Die Kreuzvalidierung ist zwar mit Rechenkosten verbunden und kann nicht alle Einschränkungen bei der Bewertung ausgleichen, doch ist sie ein unverzichtbares Instrument im Werkzeugkasten des Datenwissenschaftlers für eine genaue und zuverlässige Model Evaluation.

Konfusionsmatrix

Eine Konfusionsmatrix ist ein leistungsfähiges Instrument zur Bewertung von Klassifizierungsmodellen. Sie bietet eine tabellarische Darstellung der vorhergesagten und tatsächlichen Klassenbezeichnungen und ermöglicht eine detaillierte Analyse der Vorhersagegenauigkeit des Modells. Die Matrix ist besonders nützlich, wenn es um unausgewogene Datensätze geht oder wenn verschiedene Fehlertypen unterschiedliche Auswirkungen haben.

Eine Konfusionsmatrix ist in der Regel in vier Quadranten eingeteilt: wahr-positive (TP), wahr-negative (TN), falsch-positive (FP) und falsch-negative (FN). Jeder Quadrant steht für ein bestimmtes Ergebnis des Klassifizierungsprozesses. TP gibt die Anzahl der korrekt vorhergesagten positiven Instanzen an, TN steht für die korrekt vorhergesagten negativen Instanzen, FP bezeichnet die Instanzen, die fälschlicherweise als positiv vorhergesagt wurden, und FN zeigt die Instanzen an, die fälschlicherweise als negativ vorhergesagt wurden.

Aus der Konfusionsmatrix lassen sich verschiedene Metriken zur Model Evaluation ableiten. Einige häufig verwendete Metriken sind:

Genauigkeit: Die Gesamtgenauigkeit des Modells, berechnet als (TP + TN) / (TP + TN + FP + FN). Sie gibt einen Hinweis auf die allgemeine Vorhersageleistung des Modells.
Präzision: Sie wird auch als positiver Vorhersagewert bezeichnet und misst den Anteil der korrekt vorhergesagten positiven Instanzen an allen als positiv vorhergesagten Instanzen. Die Präzision wird als TP / (TP + FP) berechnet und ist nützlich, wenn der Schwerpunkt auf der Minimierung falsch positiver Ergebnisse liegt.
Recall: Auch bekannt als Sensitivität oder True-Positive-Rate, misst sie den Anteil der korrekt vorhergesagten positiven Instanzen an allen tatsächlich positiven Instanzen. Der Recall wird berechnet als TP / (TP + FN) und ist nützlich, wenn der Schwerpunkt auf der Minimierung von Falsch-Negativen liegt.
F1-Score: Der harmonische Mittelwert aus Precision und Recall, der ein ausgewogenes Maß für die Leistung des Modells darstellt. Er wird berechnet als 2 * (Präzision * Rückruf) / (Präzision + Rückruf).

Die Konfusionsmatrix gibt Aufschluss über die spezifischen Fehlertypen des Modells. Sie hilft zu erkennen, ob das Modell eher zu falsch-positiven oder falsch-negativen Ergebnissen neigt, was bei der weiteren Verfeinerung des Modells oder der Entscheidungsfindung hilfreich sein kann.

Es ist wichtig zu beachten, dass die Interpretation der Konfusionsmatrix und der abgeleiteten Metriken vom spezifischen Problemkontext und den relativen Kosten abhängt, die mit den verschiedenen Fehlertypen verbunden sind. Außerdem sollte die Wahl der Bewertungsmetriken mit den Zielen und Anforderungen der Klassifizierungsaufgabe übereinstimmen.

Zusammenfassend lässt sich sagen, dass eine Konfusionsmatrix einen detaillierten und detaillierten Überblick über die Leistung eines Klassifikationsmodells bietet. Sie ermöglicht die Berechnung verschiedener Evaluierungsmetriken, mit deren Hilfe die Genauigkeit, die Präzision, der Recall und der F1-Score des Modells bewertet werden können. Durch die Analyse der Konfusionsmatrix können Praktiker einen Einblick in die Mo

ROC – Kurve

Die Receiver-Operating-Characteristic-Kurve (ROC-Kurve) ist ein weit verbreitetes Instrument zur Bewertung der Leistung von binären Klassifikationsmodellen. Sie bietet eine grafische Darstellung des Kompromisses zwischen der wahr-positiven Rate (Sensitivität) und der falsch-positiven Rate (1 – Spezifität) bei verschiedenen Klassifikationsschwellenwerten.

Die ROC-Kurve wird erstellt, indem die wahr-positive Rate (TPR) auf der y-Achse gegen die falsch-positive Rate (FPR) auf der x-Achse aufgetragen wird, während die Klassifizierungsschwelle variiert wird. Jeder Punkt auf der ROC-Kurve entspricht einer bestimmten Schwellenwerteinstellung und gibt die Leistung des Modells bei diesem Schwellenwert an. Das ideale Modell hätte eine ROC-Kurve, die die obere linke Ecke des Diagramms umarmt und eine hohe TPR und niedrige FPR über alle Schwellenwerte hinweg darstellt.

ROC Curve Diagram — Struktur einer ROC – Kurve | Quelle: Autor

Einer der Hauptvorteile der ROC-Kurve ist ihre Fähigkeit, eine umfassende Bewertung der Leistung eines Modells bei verschiedenen Schwellenwerten zu liefern. Sie ermöglicht es Praktikern, den Zielkonflikt zwischen Sensitivität und Spezifität zu visualisieren und einen geeigneten Schwellenwert zu wählen, der diese beiden Faktoren je nach Problemkontext und Anforderungen ausbalanciert.

Die Fläche unter der ROC-Kurve (AUC-ROC) ist eine häufig verwendete zusammenfassende Metrik, die von der ROC-Kurve abgeleitet wird. Sie stellt die Gesamtleistung des Modells dar, unabhängig von der Schwellenwerteinstellung. Ein AUC-ROC-Wert von 0,5 bedeutet einen zufälligen Klassifikator, während ein Wert von 1,0 einen perfekten Klassifikator darstellt. Je näher der AUC-ROC-Wert bei 1,0 liegt, desto besser ist die Fähigkeit des Modells, zwischen positiven und negativen Instanzen zu unterscheiden.

Die ROC-Kurve und der AUC-ROC bieten mehrere Vorteile bei der Model Evaluation. Sie sind unempfindlich gegenüber einem Klassenungleichgewicht und werden nicht durch die Wahl eines bestimmten Schwellenwerts beeinflusst. Die Kurve bietet eine visuelle Darstellung der Diskriminierungsfähigkeit des Modells und ermöglicht den Vergleich mehrerer Modelle. Der AUC-ROC-Wert bietet eine zusammenfassende Metrik mit einem Wert, die den Vergleich und die Auswahl von Modellen vereinfacht.

Es ist jedoch wichtig zu beachten, dass die ROC-Kurve und der AUC-ROC-Wert am besten für binäre Klassifizierungsaufgaben geeignet sind. Sie sind möglicherweise nicht direkt auf Mehrklassenprobleme anwendbar, wenn nicht entsprechende Modifikationen vorgenommen werden, wie z. B. die One-vs-Rest- oder One-vs-one-Strategien. Darüber hinaus sollte die Interpretation der ROC-Kurve und der AUC-ROC in Verbindung mit den spezifischen Anforderungen und Kosten im Zusammenhang mit falsch-positiven und falsch-negativen Ergebnissen betrachtet werden.

Zusammenfassend lässt sich sagen, dass die ROC-Kurve ein wertvolles Hilfsmittel bei der Model Evaluation ist, da sie Einblicke in die Leistung eines binären Klassifikationsmodells bei verschiedenen Schwellenwerteinstellungen bietet. Sie hilft dabei, den Kompromiss zwischen Sensitivität und Spezifität zu visualisieren und ermöglicht eine fundierte Entscheidungsfindung bei der Wahl eines Schwellenwerts. Der AUC-ROC-Score bietet eine zusammenfassende Metrik für die allgemeine Diskriminierungsfähigkeit des Modells. Durch die Nutzung der ROC-Kurve und des AUC-ROC-Wertes können Praktiker ein tieferes Verständnis für die Leistung des Modells gewinnen und fundierte Entscheidungen für die Modellauswahl oder -verbesserung treffen.

Was sind die Grenzen und Vorbehalte der Model Evaluation?

Die Model Evaluation spielt zwar eine entscheidende Rolle beim maschinellen Lernen und bei der Vorhersagemodellierung, aber es ist wichtig, sich ihrer Grenzen und der damit verbundenen Vorbehalte bewusst zu sein. Das Verständnis dieser Faktoren trägt dazu bei, eine umfassendere und differenziertere Bewertung der Modellleistung zu gewährleisten. Die folgenden Überlegungen sollten berücksichtigt werden:

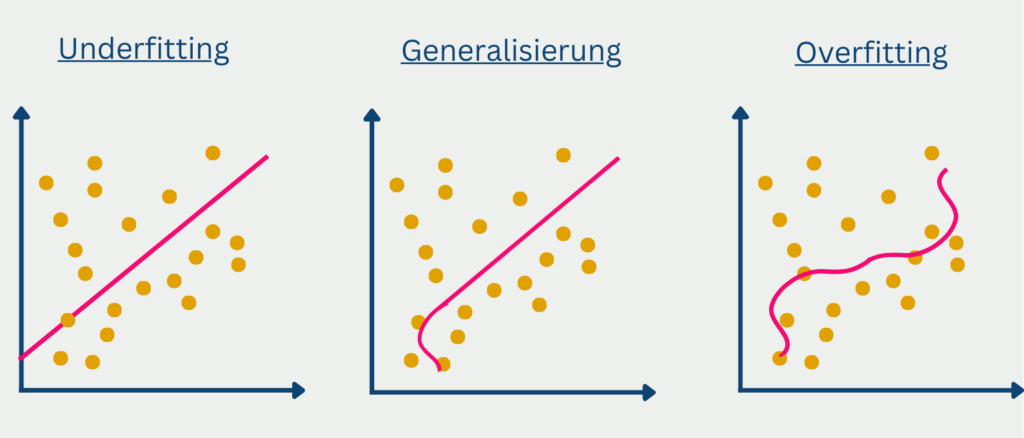
Überanpassung und Unteranpassung: Modelle können unter einer Überanpassung leiden, bei der sie in den Trainingsdaten außerordentlich gut abschneiden, aber nicht auf neue, ungesehene Daten verallgemeinert werden können. Andererseits kommt es zu einer Unteranpassung, wenn ein Modell zu einfach ist, um die zugrunde liegenden Muster in den Daten zu erfassen. Beide Szenarien können zu irreführenden Bewertungsergebnissen führen.

Unterschied zwischen Overfitting und Underfitting | Quelle: Autor

Datenqualität und Verzerrungen: Die Qualität und Repräsentativität der Trainings- und Testdaten haben einen erheblichen Einfluss auf die Model Evaluation. Verzerrungen oder Fehler in den Daten können die Leistung des Modells beeinträchtigen und zu Verzerrungen in den Bewertungsergebnissen führen. Ein gründliches Verständnis der Daten, die Berücksichtigung von Verzerrungen und die Gewährleistung einer ordnungsgemäßen Datenerfassung und -kennzeichnung sind von entscheidender Bedeutung.
Datenleckage: Ein Datenleck entsteht, wenn Informationen aus dem Testsatz das Modell während des Trainings unbeabsichtigt beeinflussen und zu übermäßig optimistischen Bewertungsergebnissen führen. Eine strikte Trennung von Trainings- und Testdaten ist unerlässlich, um Datenverluste zu vermeiden und zuverlässige Leistungsschätzungen zu erhalten.
Begrenzte Verallgemeinerung: Modelle, die auf einem bestimmten Datensatz oder in einem bestimmten Kontext gut funktionieren, lassen sich möglicherweise nicht gut auf andere Datensätze oder reale Szenarien übertragen. Die Bewertung der Leistung eines Modells in verschiedenen Datensätzen oder die Durchführung einer Kreuzvalidierung hilft, seine Verallgemeinerungsfähigkeiten zu verstehen.
Bewertungsmetriken und Ziele: Die Auswahl der Metriken für die Model Evaluation sollte sich an den Zielen und Anforderungen der jeweiligen Aufgabe orientieren. Verschiedene Metriken betonen unterschiedliche Aspekte der Modellleistung, und die Verwendung einer einzigen Metrik liefert möglicherweise keine umfassende Bewertung. Es sollten mehrere Metriken in Betracht gezogen und ihre Ergebnisse gemeinsam interpretiert werden.
Unausgewogene Klassen oder schiefe Verteilungen: Bei Klassifizierungsaufgaben können unausgewogene Klassenverteilungen die Bewertungsergebnisse beeinflussen. So kann beispielsweise die Genauigkeit eine irreführende Bewertung liefern, wenn die Klassen unausgewogen sind. Metriken wie Präzision, Recall oder F1-Score, die für unausgewogene Datensätze besser geeignet sind, sollten in Betracht gezogen werden.
Domänenspezifische Überlegungen: Verschiedene Bereiche und Anwendungen haben einzigartige Merkmale und Anforderungen, die bei der Model Evaluation berücksichtigt werden sollten. Das Verständnis der spezifischen Domäne, der geschäftlichen Einschränkungen und der ethischen Erwägungen ist für die Interpretation und Validierung der Leistung des Modells von wesentlicher Bedeutung.
Externe Faktoren und sich verändernde Umgebungen: Modelle können durch externe Faktoren oder sich verändernde Umgebungen beeinflusst werden, die während der Model Evaluation nicht erfasst wurden. Der Einsatz in der realen Welt kann neue Herausforderungen mit sich bringen, und die Leistung des Modells kann sich mit der Zeit verschlechtern. Eine kontinuierliche Überwachung und Aktualisierung des Modells ist notwendig, um veränderten Bedingungen Rechnung zu tragen.
Interpretierbarkeit und Erklärbarkeit: Einige Modelle, wie z. B. Deep-Learning-Modelle, sind sehr komplex und lassen sich nur schwer interpretieren. Sie können zwar eine hervorragende Leistung aufweisen, aber ihre Blackbox-Natur kann ihren praktischen Nutzen einschränken. Das Gleichgewicht zwischen Modellleistung und Interpretierbarkeit ist von entscheidender Bedeutung, insbesondere in Bereichen, in denen die Erklärbarkeit entscheidend ist.

Eine kritische Herangehensweise an die Model Evaluation, die diese Einschränkungen und Vorbehalte berücksichtigt, trägt zu einer solideren Bewertung bei. Zwar ist kein Evaluierungsprozess fehlerfrei, doch die Kombination von Evaluierungstechniken, die Durchführung strenger Experimente und die Nutzung von Fachwissen tragen zu einer zuverlässigen Bewertung bei.

Das solltest Du mitnehmen

Die Model Evaluation ist entscheidend für die Beurteilung der Leistung von Modellen des maschinellen Lernens.
Zu den gängigen Techniken für die Model Evaluation gehören die Aufteilung zwischen Training und Test, die Kreuzvalidierung und Leistungsmetriken wie Genauigkeit, Präzision, Wiedererkennung und F1-Score.
Die Kreuzvalidierung hilft dabei, den Kompromiss zwischen Verzerrung und Varianz zu überwinden, indem sie eine Schätzung der Modellleistung für neue Daten liefert.
Der Kompromiss zwischen Verzerrung und Varianz ist wichtig, weil er dazu beiträgt, den Kompromiss zwischen Modellkomplexität und Genauigkeit auszugleichen.
Die Model Evaluation hat ein breites Spektrum an realen Anwendungen, unter anderem in den Bereichen Finanzen, Gesundheitswesen und Marketing.
Eine genaue Model Evaluation ist für den Aufbau effektiver maschineller Lernsysteme, die in einer Vielzahl von Bereichen von Nutzen sein können, unerlässlich.