Die Regularisierung ist eine sehr wichtige Methode im Bereich des Machine Learnings, die dafür sorgt, Modelle robuster zu machen und besser auf neue Daten zu generalisieren. Beim Training von Modellen spielt häufig das sogenannte Overfitting eine große Rolle. Es tritt auf, wenn das Modell sich zu stark an die Trainingsdaten anpasst und deswegen nur schlecht auf neue, ungesehene Daten reagiert. Hier kommt die Regularisierung ins Spiel und sorgt dafür, dass das Modell generelle Strukturen erlernt und nicht nur das Rauschen des Trainingsdatensatzes imitiert. 

In diesem Artikel schauen wir uns deshalb die größten Probleme beim Modelltraining an, um dann die verschiedenen Regularisierungstechniken im Detail zu verstehen. Dazu versuchen wir auch die mathematische Implementierung zu verstehen und üben, wie sich die Regularisierung in Python integrieren lässt. Zum Schluss beschäftigen wir uns noch mit weiterführenden Regularisierungstechniken, die sich beispielsweise auf neuronale Netze spezialisieren lassen oder bereits vor dem Modelltraining ansetzen. 

Was ist die Regularisierung?

Die Regularisierung umfasst verschiedene Methoden, welche in der Statistik und dem Machine Learning eingesetzt werden, um die Komplexität eines Modells zu kontrollieren. Sie hilft, robust auf neue und ungesehene Daten zu reagieren und dadurch die Generalisierbarkeit des Modells zu ermöglichen. Dies wird bewirkt, indem die Regularisierung der Optimierungsfunktion des Modells einen Strafterm hinzufügt, um zu verhindern, dass sich das Modell zu stark auf die Trainingsdaten anpasst. Dadurch wird das Modell weniger anfällig lediglich den Fehler und das Rauschen der Trainingsdaten zu erlernen, welcher in der späteren Anwendung möglicherweise nicht mehr vorhanden ist. 

Die Hauptziele der Regularisierung bestehen darin, zu verhindern, dass das Modell sich überanpasst, also zu stark versucht die Trainingsdaten zu imitieren und dadurch nur schlecht generalisiert. Dadurch führt die Regularisierung außerdem dazu, dass das Gleichgewicht zwischen Verzerrung und Varianz stabil gehalten wird. Was es mit diesen beiden Konzepten auf sich hat, schauen wir uns in den folgenden Abschnitten noch genauer an. 

Was ist Overfitting?

Als Überanpassung, oder englisch Overfitting, bezeichnet man die Situation, dass sich ein Modell zu stark an die Trainingsdaten angepasst hat und nicht gut auf ungesehene Daten generalisiert. Man erkennt dies daran, dass die Ergebnisse für Vorhersagen im Trainingsdatensatz sehr gut sind, aber das Modell für neue, ungesehene Daten nur sehr niedrige Genauigkeiten erzielt. 

In den meisten Fällen wird die Überanpassung durch zwei Ursachen hervorgerufen. Wenn das Modell zu komplex ist, also zu viele Parameter enthält, dann hat es zu viele Möglichkeiten, die Details des Trainingsdatensatzes zu erlernen, die aber möglicherweise außerhalb des Datensatzes gar nicht vorkommen. 

Außerdem kann es zu Overfitting kommen, wenn nur eine begrenzte Datenmenge zur Verfügung steht oder der Trainingsdatensatz nicht der allgemeinen Verteilung, wie sie in der Realität vorkommt, entspricht. Wenn man beispielsweise ein Modell trainieren will, das für die gesamte Bevölkerung eines Landes Vorhersagen treffen soll, dann kommt es sehr wahrscheinlich zu Overfitting, wenn man dafür einen Datensatz verwendet in dem nur Menschen unter 30 Jahren vorhanden sind.

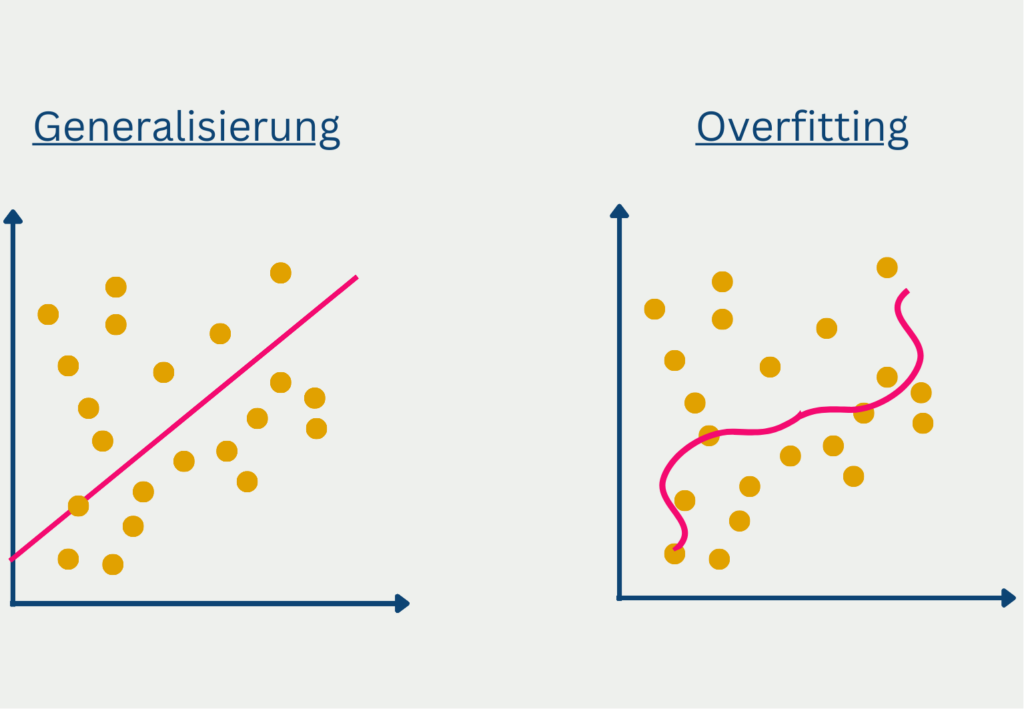
Ein weiterer möglicher Grund für Overfitting kann schließlich eine zu hohe Zahl an Trainingsiterationen sein. In jedem Durchlauf versucht das Modell eine Verbesserung zu erzählen, also mehr richtige Vorhersagen auf dem Trainingsdatensatz zu treffen im Vergleich zum vorherigen Durchlauf. Ab einem gewissen Punkt ist dies nur möglich, wenn es noch stärker auf die Eigenschaften des Trainingsdatensatzes eingeht und sich an diese anpasst. 

Im Allgemeinen gibt es keine Kennzahl oder eine Analyse, die mit Sicherheit zurückgibt, ob ein Modell überangepasst ist oder nicht. Es gibt jedoch einige Parameter und Analysen, die auf ein Overfitting hinweisen können. 

Die Verlustfunktion misst, wie oft das Modell eine richtige Vorhersage trifft. Bei einem guten Modell, das auch gut auf ungesehene Daten generalisiert, sinkt die Verlustfunktion im Trainingsdatensatz und (!) im Validierungsdatensatz mit zunehmenden Trainingsdaten. Dies spricht dafür, dass das Modell die zugrundeliegende Datenstruktur erkennt und auch für neue Daten gute Vorhersagen liefert. Bei einem überangepassten Modell hingegen sinkt die Verlustfunktion im Validierungsdatensatz und beginnt ab einem gewissen Punkt wieder zu steigen. Das deutet darauf hin, dass das Modell sich nun zu stark an die Trainingsdaten anpasst und deshalb die Ergebnisse für ungesehene Daten im Validierungsset schlechter werden. 

Was ist der Bias-Variance Tradeoff?

Der Bias-Variance Tradeoff beschreibt ein grundlegendes Problem im Machine Learning, welches besagt, dass man einen Kompromiss eingehen muss zwischen einem möglichst einfachen Modell und einem sehr anpassungsfähigen Modell, das gute Ergebnisse auch für neue Daten liefert. 

Bei jedem Training stehen die zwei zentralen Aspekte Bias und Varianz im Konflikt. Bevor wir uns diese Problematik genauer anschauen können, sollten wir verstehen was der Bias und die Varinaz genau sind. 

Der Bias, oder auf deutsch Verzerrung, beschreibt das Problem, dass ein zu einfaches Modell die zugrundeliegenden Strukturen in den Daten nicht erkennt und deshalb immer abweichende Werte vorhersagt und somit ein gewisser Restfehler bleibt. Jedoch will man im Training das Modell auch nicht zu komplex bauen, um ein Overfitting zu verhindern, was wiederum eine schlechte Generalisierung auf ungesehene Daten bedeuten würde.

Die Varianz hingegen beschreibt, wie stark die Vorhersagen eines Modells schwanken, wenn sich die Eingabewerte nur minimal ändern. Eine hohe Varianz würde bedeuten, dass leichte Änderungen beim Input zu sehr starken Änderungen der Vorhersagen führen würden.

Ein gutes Machine Learning Modell sollte eine möglichst geringe Varianz haben, damit leichte Änderungen nur geringe Auswirkungen auf die Vorhersagen haben und das Modell somit zuverlässige und belastbare Predictions liefert. Gleichzeitig sollte jedoch auch die Verzerrung gering sein, sodass die Vorhersage möglichst nahe am tatsächlichen Ergebnis liegt. Das problematische an diesem Ziel ist nun jedoch, dass ein Modell mit einem geringen Bias eine hohe Varianz zur Folge hat und umgekehrt.  

Dadurch ergibt sich der Gewissenskonflikt, der mit dem Bias Variance Tradeoff zusammengefasst wird. Um ein geringeres Bias zu erzielen, muss das Modell komplexer werden, was jedoch wiederum zu einem potenziellen Overfitting und einer höheren Varianz führt. Im umgekehrten Fall kann die Varianz vermindert werden, indem die Komplexität des Modells reduziert wird, was jedoch wieder einen steigenden Bias zur Folge hat. 

Die Kunst besteht nun darin, einen guten Kompromiss zwischen einem vertretbaren Maß an Verzerrung und einem vertretbaren Maß an Varianz zu finden. Es ist wichtig diesen grundlegenden Zusammenhang zu verstehen, um diesen in allen Bereichen des Modelltrainings zu berücksichtigen und zu integrieren. 

Welche Arten der Regularisierung gibt es?

Die Regularisierung umfasst verschiedene Techniken, welche das Ziel haben, Machine Learning Modelle zu verbessern, indem sie die Modellkomplexität kontrollieren und die Überanpassung verhindern. Über die Zeit haben sich verschiedene Arten der Regularisierung entwickelt mit ihren eigenen Vor- und Nachteilen, welche wir in diesem Abschnitt genauer vorstellen werden. 

L1 – Regularisierung (Lasso)

Die L1-Regularisierung, oder auch Lasso (Least Absolute Shrinkage and Selection Operator), verfolgt das Ziel, die absolute Summe aller Netzwerkparameter zu minimieren. Dadurch wird das Modell also bestraft, wenn die Größe der Parameter zu stark ansteigt. Durch dieses Vorgehen kann es bei der L1-Regularisierung dazu kommen, dass einzelne Modellparameter auf null gesetzt werden, wodurch bestimmte Merkmale im Datensatz nicht mehr beachtet werden. Dadurch entsteht ein kleineres Modell mit weniger Komplexität, welches nur die wichtigsten Merkmale für die Vorhersage umfasst. 

Mathematisch gesehen, wird ein weiterer Term in die Kostenfunktion hinzugefügt. In unserem Beispiel gehen wir von einer Verlustfunktion mit einem Mean Squared Error aus, bei dem die durchschnittliche, quadrierte Abweichung zwischen dem tatsächlichen Wert aus dem Datensatz und der Vorhersage errechnet wird. Umso geringer diese Abweichung, umso besser ist das Modell darin, möglichst genaue Vorhersagen zu treffen. 

Für ein Modell mit dem Mean Squared Error als Verlustfunktion und einer L1-Regularisierung ergibt sich dann die folgende Kostenfunktion: 

\(\) \[J\left(\theta\right)=\frac{1}{m}\sum_{i=1}^{m}\left(y_i-\widehat{y_i}\right)^2+\lambda\sum_{j=1}^{n}\left|\theta_j\right|\]

• \(J\) ist die Kostenfunktion. 
• \(\lambda\) ist der Regularisierungsparameter, der mitbestimmt, wie stark die Regularisierung einen Einfluss auf den Fehler des Modells hat.
• \(\sum_{j=1}^{n}\left|\theta_j\right|\) ist die Summe aller Parameter des Modells.

Das Ziel des Modells ist es, diese Kostenfunktion zu minimieren. Wenn also die Summe der Parameter anwächst, dann steigt die Kostenfunktion und es gibt einen Anreiz, dem entgegenzuwirken. \(\lambda\) kann dabei jeden positiven Wert (>= 0) annehmen. Ein Wert nahe 0 steht dabei für eine weniger starke Regularisierung, während ein großer Wert für eine starke Regularisierung steht. Mithilfe von beispielsweise der Cross-Validation können verschiedene Modell mit unterschiedlich starker Regularisierung getestet werden, um das optimale Gleichgewicht, abhängig von den Daten, zu finden.

Vorteile der L1 – Regularisierung:

• Merkmalsauswahl: Dadurch, dass das Modell dafür incentiviert wird, die Größe der Parameter nicht zu stark ansteigen zu lassen, werden ein paar der Parameter auch gleich 0 gesetzt. Dadurch werden gewisse Merkmale aus dem Datensatz entfernt und es findet automatisch eine Auswahl der wichtigsten Merkmale statt.
• Einfachheit: Ein Modell mit weniger Merkmalen kann einfacher verstanden und interpretiert werden. 

Nachteile der L1 – Regularisierung: 

• Probleme bei korrelierten Variablen: Wenn mehrere Variablen in dem Datensatz miteinander korreliert sind, neigt Lasso dazu, nur eine der Variablen zu behalten und die anderen, korrelierten Variablen auf null zu setzen. Dadurch können Informationen verloren gehen, welche in den anderen Variablen vorhanden gewesen wären. 

L2 – Regularisierung (Ridge)

Die L2 – Regularisierung versucht dem Problem von Lasso, also dem Entfernen von Variablen, die noch Informationen enthalten, dadurch zu begegnen, dass das Quadrat der Parameter als Regularisierungsterm verwendet wird. Somit fügt sie dem Modell eine Strafe hinzu, die proportional zu dem Quadrat der Parameter ist. Dies hat zur Folge, dass die Parameter nicht komplett auf null gehen, sondern lediglich kleiner werden. Umso näher ein Parameter mathematisch gesehen der Null kommt, umso kleiner wird sein quadrierter Einfluss auf die Kostenfunktion. Deshalb konzentriert sich das Modell vorher auf andere Parameter, bevor es einen Parameter nahe null komplett streicht. 

Mathematisch gesehen sieht die Ridge Regularisierung für ein Modell mit dem Mean Squared Error als Verlustfunktion wie folgt aus: 

\(\)\[J\left(\theta\right)=\frac{1}{m}\sum{\left(i=1\right)^m\left(y_i-\widehat{y_i}\right)^2}+\lambda\sum_{j=1}^{n}{\theta_j^2}\]

Die Parameter sind dabei identisch zu der vorherigen Formel mit dem Unterschied, dass nicht der absolute Wert theta aufsummiert wird, sondern das Quadrat. 

Vorteile der L2 – Regularisierung:

• Stabilisierung: Durch die Ridge Regularisierung wird dafür gesorgt, dass die Parameter deutlich stabiler auf kleine Änderungen in den Trainingsdaten reagieren.  
• Handhabung von Multikollinearität: Bei mehreren, korrelierten Variablen sorgt die L2 – Regularisierung dafür, dass diese gemeinsam betrachtet werden und nicht lediglich eine Variable im Modell behalten wird, während die anderen rausgeworfen werden. 

Nachteile der L2 – Regularisierung:

• Keine Merkmalsauswahl: Dadurch, dass Ridge die Parameter nicht auf null setzt, bleiben alle Merkmale aus dem Datensatz im Modell erhalten, wodurch die Interpretierbarkeit schlechter ist, da mehr Variablen berücksichtig werden. 

Elastic Net

Das Elastic Net versucht das Beste aus den beiden Welten zu kombinieren, indem es sowohl einen Term aus der L1 – Regularisierung, als auch einen Term aus der L2 – Regularisierung in die Kostenfunktion inkludiert. Dadurch ermöglicht es, dass sowohl eine Merkmalsauswahl stattfindet und gleichzeitig multikollineare Variablen erhalten bleiben. Über die beiden Parameter \(\lambda_1\) und \(\lambda_2\) kann das Gleichgewicht zwischen den beiden Regularisierungen eingestellt werden. 

\(\)\[J\left(\theta\right)=\frac{1}{m}\sum_{i=1}^{m}\left(y_i-\widehat{y_i}\right)^2+\alpha\left(\lambda_1\sum_{j=1}^{n}\left|\theta_j\right|+\lambda_2\sum_{j=1}^{n}\theta_j^2\right)\]

Dabei bestimmt der Parameter \(\alpha\) darüber, welchen Einfluss die Regularisierung insgesamt auf die Kostenfunktion hat und \(\lambda_1\) und \(\lambda_2\) zeigen an, wie das Gleichgewicht zwischen beiden Methoden ist. 

Wie kann man die Regularisierung in Python umsetzen?

In Python gibt es die Möglichkeit mithilfe des Moduls Scikit-Learn direkt Regressionen zu importieren, welche die entsprechenden Regularisierungsmethoden bereits inkludiert haben. In diesem Abschnitt werden wir insgesamt drei Modelle auf zufällige Trainingsdaten trainieren und die Ergebnisse jeweils vergleichen. 

Dazu importieren wir im ersten Schritt die nötigen Module. Neben Scikit-Learn, was wir für die Modelle und deren Verlustfunktionen benötigen, importieren wir auch NumPy für die Generierung der zufälligen Trainingsdaten und Matplotlib, um am Ende die unterschiedlichen Ergebnisse visualisieren zu können. 

Für die Generierung eines beispielhaften Trainingsdatensatzes nutzen wir NumPy und setzen np.random.seed(42), damit bei mehreren Durchläufen des Programms immer dieselben Daten generiert werden. Insgesamt werden wir 100 Datenpunkte mit jeweils fünf Merkmalen haben, welche mit np.random.rand erstellt werden. Für jedes der Merkmale definieren wir einen Parameter, den das Modell im Lauf des Trainings erlernen soll. 

Damit diese Parameterwerte im Datensatz erkannt und erlernt werden können, multiplizieren wir unsere Datenpunkt mit den Parametern, wodurch sich die Zielvariable y ergibt. Damit es das Modell dabei nicht zu einfach hat, ergänzen wir ein Rauschen, welches dazuaddiert wird. 

Abschließend teilen wir den Datensatz in Trainings- und Testdatensat auf, damit wir später die Ergebnisse der Modelle auf neuen, ungesehenen Daten vergleichen können. 

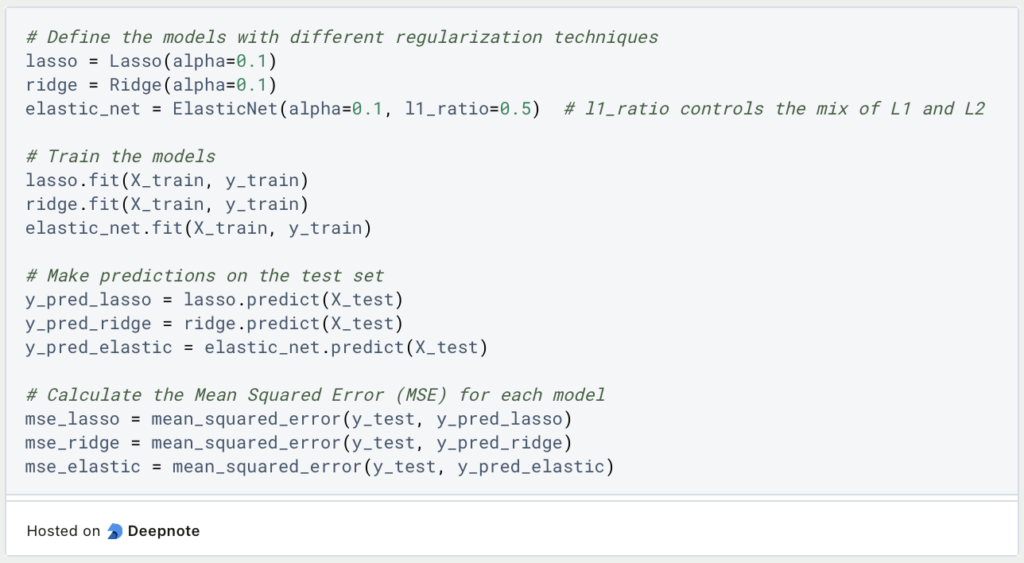
Nun kommt der spannende Teil in dem wir die einzelnen Modelle erstellen und trainieren lassen. Für lasso und ridge müssen wir lediglich die Größe der Regulierung über den Hyperparameter alpha hinterlegen. Beim ElasticNet hingegen müssen wir noch zusätzlich das Verhältnis zwischen lasso und ridge festlegen. Ein guter Startpunkt dafür ist 0.5 wodurch die beiden Regularisierungsmethoden gleich stark gewichtet werden. 

Anschließend trainieren wir die einzelnen Modelle und lassen sie Vorhersagen für das Testset treffen. Damit wir diese Ergebnisse neutral vergleichen können, berechnen für jede Kombination aus Testset und Vorhersage den Mean Squared Error, was bereits ein gutes Bild über die Leistungsfähigkeit der verschiedenen Modelle geben sollte. 

Diese Ergebnisse werden nun ausgegeben und außerdem schauen wir uns die erlernten Werte der Parameter an, um zu sehen, wie nahe sie dem vorher definierten Ergebnis gekommen sind. 

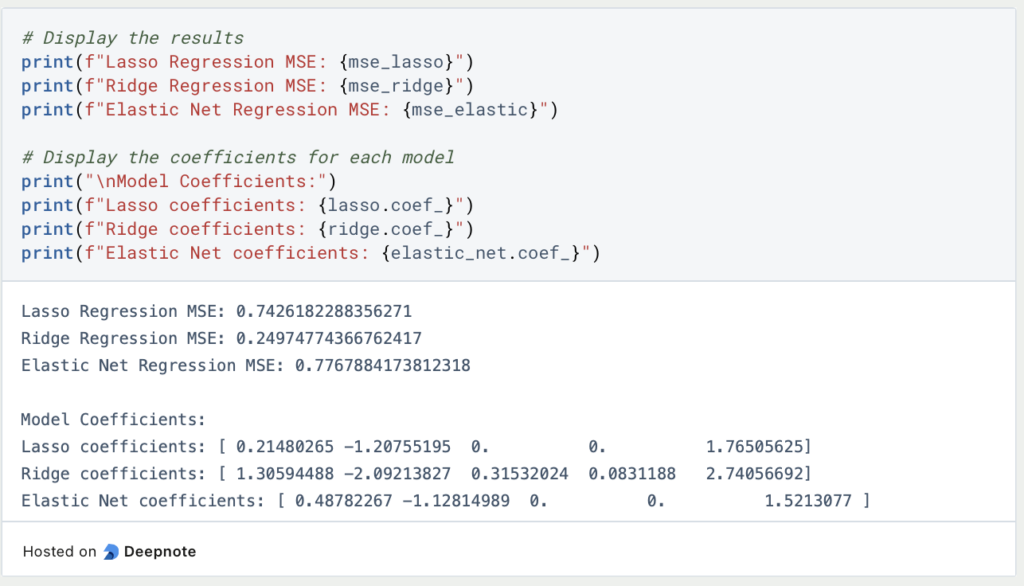
Wir wir sehen können, waren, wie erwartet, nur Lasso und Elastic Net in der Lage die Parameter drei und vier richtig vorherzusagen, da Ridge nicht in der Lage ist, einen Parameter auf null zu setzen. Insgesamt hat jedoch die Ridge Regression in diesem Beispiel am besten abgeschnitten und schlägt die beiden anderen Regularisierungsmethoden deutlich.

In dem folgenden Diagramm wird nochmal deutlich, wie die einzelnen Modelle die Parameter geschätzt haben.

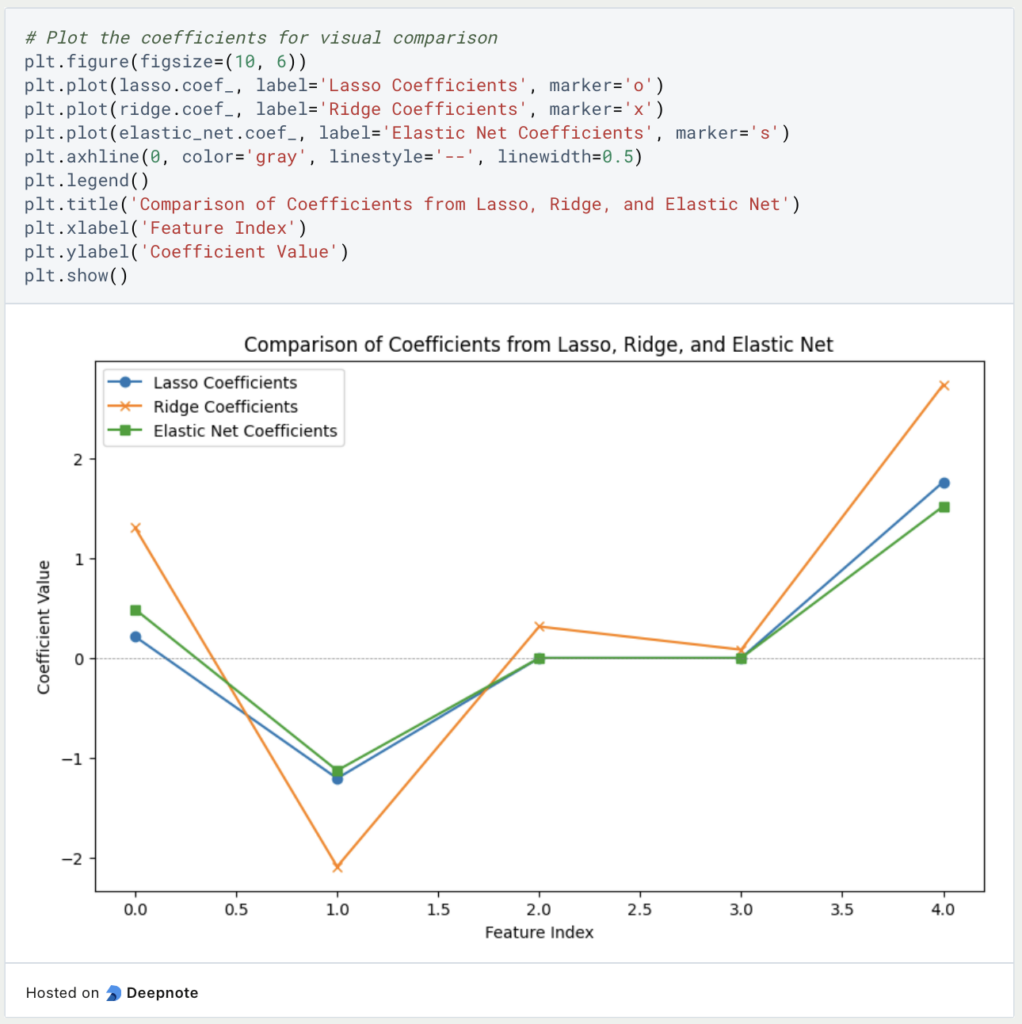
Ein möglicher Ansatzpunkt wäre nun beim ElasticNet nochmal mit einer anderen Gewichtung zwischen Ridge und Lasso zu arbeiten und die Tendenz eher zu Ridge zu legen. Damit könnte man testen, ob diese Veränderung bessere Ergebnisse liefert. 

Was sind erweiterte Regularisierungstechniken?

Die bisher vorgestellten Regularisierungstechniken sind besonders für Regressionen und andere, klassische Machine Learning Modelle geeignet. Darüber hinaus haben sich jedoch auch Methoden entwickelt, die vor allem für Deep Learning und Neuronale Netzwerke gut funktionieren und die wir in diesem Abschnitt genauer vorstellen. 

Dropout Layer

Bei einem neuronalen Netzwerk entsteht die Vorhersage, indem verschiedene Schichten mit Neuronen durchlaufen werden, die alle eine eigene Gewichtung haben, welche sich, während dem Training ändern kann. Das Ziel des Modells ist es durch diese Veränderungen die Verlustfunktion zu minimieren und dadurch bessere Vorhersagen zu treffen. 

In einer Dropout Layer werden bestimmte Neuronen in einem Trainingsdurchlauf auf den Wert Null gesetzt, also aus dem Netzwerk entfernt. Somit haben sie bei der Vorhersage und auch bei der Backpropagation keinerlei Einfluss. Dadurch wird in jedem Durchlauf eine neue, leicht abgeänderte Netzwerkarchitektur gebaut und das Netzwerk erlernt, auch gute Vorhersagen ohne bestimmte Inputs zu erzeugen.

In tiefen Neuronalen Netzwerken entsteht Overfitting meist dadurch, dass bestimmte Neuronen von verschiedenen Schichten sich gegenseitig beeinflussen. Einfach gesagt führt das zum Beispiel dazu, dass gewisse Neuronen die Fehler von vorherigen Knoten ausbessern und somit voneinander abhängen oder die guten Ergebnisse der vorherigen Schicht ohne große Änderungen einfach weiterreichen. Dadurch wird eine schlechte Generalisierung erreicht. 

Durch die Nutzung der Dropout Layer können sich die Neuronen hingegen nicht mehr auf die Knoten von vorherigen oder folgenden Schichten verlassen, da sie nicht davon ausgehen können, dass diese in dem jeweiligen Trainingsdurchlauf überhaupt existieren. Dies führt dazu, dass die Neuronen, nachweislich, grundlegendere Strukturen in Daten erkennt, die nicht von der Existenz einzelner Neuronen abhängen. Diese Abhängigkeiten treten in regulären Neuronalen Netzwerken tatsächlich häufig auf, da dies eine einfache Möglichkeit ist, die Verlustfunktion schnell zu verringern und dadurch dem Ziel des Modells schnell näher zu kommen. 

Außerdem verändert, wie bereits erwähnt, der Dropout die Architektur des Netzwerks leicht. Somit ist das austrainierte Modell dann eine Kombination aus vielen, leicht unterschiedlichen Modellen. Diese Vorgehensweise kennen wir bereits aus dem Ensemble Learning, wie beispielsweise in Random Forests. Dabei stellt sich heraus, dass das Ensemble von vielen, relativ ähnlichen Modellen meist bessere Ergebnisse liefert als ein einziges Modell. Dieses Phänomen ist unter dem Namen “Wisdom of the Crowds” bekannt.

Data Augmentation

In vielen Anwendungen, vor allem im Bereich des Supervised Learnings, sind die zur Verfügung stehenden Datensätze und deren Größe limitiert. Gleichzeitig sind sie jedoch auch oft zu klein, um komplexe Modelle trainieren zu können, sodass es zum Overfitting kommt. Die Data Augmentation bietet eine Möglichkeit, den Datensatz künstlich zu vergrößern, indem bestehende Datenpunkt leicht abgewandelt werden und dem Datensatz zusätzlich hinzugefügt werden. In der Bildverarbeitung kann dies dann zum Beispiel bedeuten, dass ein Bild einmal in Farbe, einmal in schwarz-weiß und einmal leicht gedreht im Datensatz vorkommt. 

Durch diese Vorgehensweise vergrößert sich nicht nur der Datensatz, sondern das Modell lernt auch besser zu generalisieren, da es eine größere Variabilität in den Trainingsdaten gibt und somit auch das Risiko für Overfitting verringert wird. 

Early Stopping

Beim Training von Deep Learning Modellen durchläuft das Training verschiedene Epochen. In jeder Epoche wird jeder Datenpunkt im Datensatz einmal in das Netzwerk gegeben. Im Vorhinein ist es schwierig festzulegen, wie viele Epochen benötigt werden, bis das Netzwerk die grundlegenden Strukturen erkannt und erlernt hat. Wenn jedoch das Training zu lange dauert, versucht das Modell weiterhin zu Verlustfunktion zu minimieren. Ab einem gewissen Zeitpunkt ist dies jedoch nur noch möglich, wenn das Modell sich noch stärker an die Trainingsdaten anpasst, also ins Overfitting kommt. 

Um diesen Punkt abpassen zu können, den man vor dem Training nicht kennt, wird die Early Stopping Rule verwendet, die das Training automatisch beendet, wenn sich die vorher festgelegte Metrik über einen gewissen Zeitraum von Epochen nicht mehr verbessert. In vielen Fällen wird dafür beispielsweise die Genauigkeit auf dem Validierungsset verwendet, welche eine besondere Teilmenge des Datensatzes darstellt, welche nach jeder Epoche genutzt wird, um festzustellen, wie das Modell auf ungesehene Daten reagiert. Wenn sich die Genauigkeit auf dem Validierungsset für mehrere Epochen nicht erhöht, dann stoppt das Training atuomatisch.

Das solltest Du mitnehmen

• Die Regularisierung umfasst Methoden im Machine Learning, die das Overfitting begrenzen sollen und beim Umgang mit dem Bias-Variance Tradeoff helfen.
• Dabei wird der Verlustfunktion ein weiterer Regularisierungsterm hinzugefügt.
• Man unterscheidet dabei die L1-Regularisierung, auch Lasso genannt, die L2-Regularisierung, auch Ridge genannt, und das Elastic Net.
• In Python kann man diese Methoden direkt mithilfe von Scikit-Learn umsetzen.
• Für neuronale Netzwerke gibt es andere Möglichkeiten Overfitting zu verhindern, beispielsweise mithilfe von Dropout Layern oder durch eine Early Stopping Rule.

Vielen Dank an Deepnote für das Sponsoring dieses Artikels! Deepnote bietet mir die Möglichkeit, Python-Code einfach und schnell auf dieser Website einzubetten und auch die zugehörigen Notebooks in der Cloud zu hosten.

Andere Beiträge zum Thema Regularisierung

Dieser Link führt Dich zu meiner Deepnote-App, in der Du den gesamten Code findest, den ich in diesem Artikel verwendet habe, und ihn selbst ausführen kannst.