Neuronale Netzwerke haben sich seit einigen Jahren als leistungsstarke Methode im Bereich der Machine Learning Modelle etabliert. Die Aktivierungsfunktion ist eine zentrale Komponente in jedem neuronalen Netz, welche einen erheblichen Einfluss auf die Funktionalität des Modells hat. Sie bestimmt, wie stark ein Neuron im Netzwerk aktiviert wird und entscheidet dadurch, welche Strukturen aus den Daten erlernt werden. Ohne die Aktivierungsfunktionen könnten die Neuronalen Netzwerke lediglich lineare Zusammenhänge erkennen und wären nicht in der Lage die beeindruckenden Ergebnisse zu produzieren, welche uns in den letzten Jahren in Atem gehalten haben. 

In diesem Beitrag beschäftigen wir uns im Detail mit den Eigenschaften einer Aktivierungsfunktion und stellen die verschiedenen Funktionen, die häufig verwendet werden, gegenüber. Außerdem geben wir Tipps, wie die richtige Aktivierungsfunktion für die Netzwerkarchitektur und den spezifischen Anwendungsfall gefunden werden kann, um ein optimales Modell zu trainieren. Bevor wir jedoch in die Thematik einsteigen können, sollten wir verstehen, wie neuronale Netzwerke und genauer gesagt die Neuronen darin funktionieren, um zu sehen, in welches System die Aktivierungsfunktion eingebettet ist. 

Wie funktioniert ein Perceptron?

Das Perceptron ist ein ursprünglich mathematisches Modell und wurde, aufgrund der Eigenschaft komplexe Zusammenhänge erlernen zu können, erst später in der Informatik und im Machine Learning genutzt. In der einfachsten Form besteht es aus genau einem sogenannten Neuron, das den Aufbau des menschlichen Gehirns nachahmt.

Das Perceptron hat dabei mehrere Eingänge, die sogenannten Inputs, an denen es numerische Informationen, also Zahlenwerte erhält. Je nach Anwendung kann sich die Zahl der Inputs unterscheiden. Die Eingaben haben verschiedene Gewichte, die angeben, wie einflussreich die Inputs für die schlussendliche Ausgabe sind. Während des Lernprozesses werden die Gewichte so geändert, dass möglichst gute Ergebnisse entstehen. 

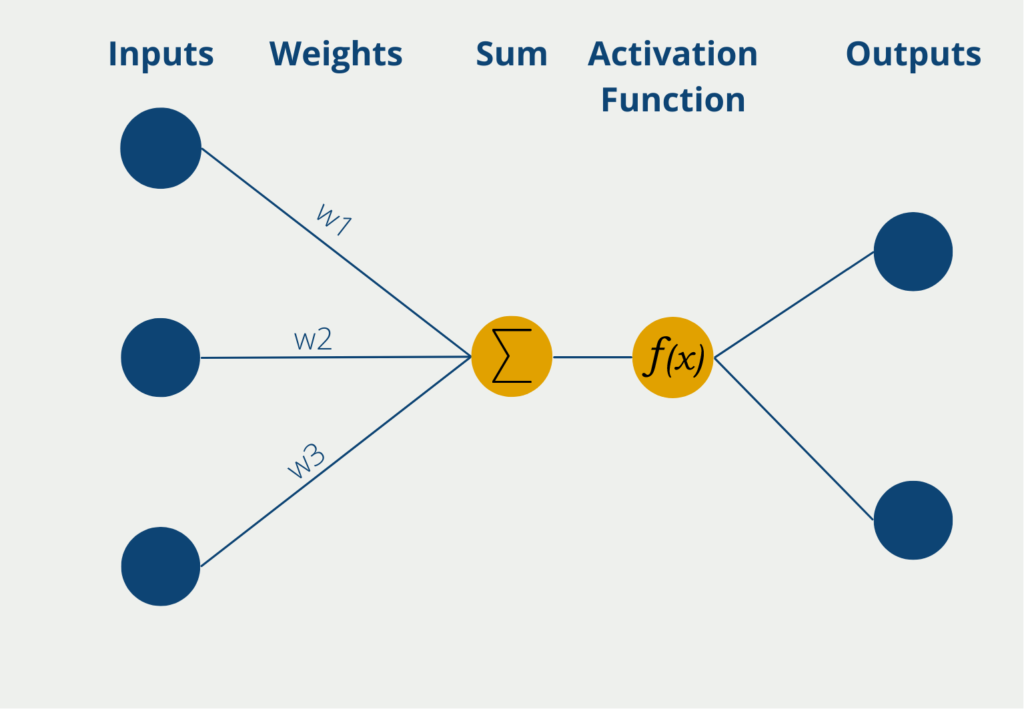
Das Neuron selbst bildet dann die Summe der Inputwerte multipliziert mit den Gewichten der Inputs. Diese gewichtete Summe wird weitergeleitet an die sogenannte Aktivierungsfunktion, welche die Logik enthält, die im Modell erlernt wird. In der einfachsten Form hat das Neuron nur einen Output, der binäre Werte, wie „Ja/Nein“ oder „Aktiv/Inaktiv“, annehmen kann. Die Aktivierungsfunktion hat dann entsprechend die Eigenschaft kontinuierliche Werte auf 0 oder 1 zu mappen. Der Output ist dann die Vorhersage des Perceptrons. 

Ein neuronales Netzwerk besteht aus Millionen oder sogar Milliarden solcher Neuronen, die dann in verschiedenen Schichten organisiert werden. Durch diese Struktur sind sie in der Lage auch komplexere Zusammenhänge in den Daten zu erkennen und zu erlernen. 

Als Beispiel für die Funktionsweise eines Perceptrons schauen wir uns die Arbeit einer Politikerin genauer an. Sie ist Mitglied des Parlaments und es muss über ein neues Gesetz abgestimmt werden. Somit muss die Politikerin entscheiden, ob sie dem Gesetzesvorschlag zustimmt oder ihn ablehnt (eine Enthaltung ist in unserem Beispiel nicht möglich). Das Perceptron hat also einen binären Output, nämlich Zustimmung oder Ablehnung. 

Als Inputs für Ihre Entscheidung stehen der Politikerinnen verschiedene Informationsquellen zur Verfügung. Zum einen gibt es ein Informationspapier mit Hintergründen, das vom Parlament ausgegeben wurde. Des Weiteren kann sich die Abgeordnete im Internet über verschiedene Sachverhalte informieren oder mit anderen Kollegen darüber diskutieren. Die Politikerin gewichtet ihre Eingaben, also ihre Informationsquellen, je nachdem wie vertrauenswürdig sie diese ansieht. Dem Informationspapier des Parlaments beispielsweise weist sie ein eher geringes Gewicht zu, da sie fürchtet, dass die Recherche nicht ausführlich genug ist und bereits in eine gewisse Richtung tendieren soll. Sie nimmt dann die Summe der Informationen, die ihr zur Verfügung stehen, zusammen mit den Gewichtungen und gibt sie weiter zur Aktivierungsfunktion. 

Diese können wir uns wie den Kopf der Politikerin vorstellen, welcher anhand der Inputs entscheidet, ob sie dem Gesetzesvorschlag zustimmen soll oder nicht. Dabei können bereits Kleinigkeiten in den Inputs zu einer massiven Meinungsänderung der Politikerin führen.

Was ist eine Aktivierungsfunktion?

Die Aktivierungsfunktion ist eine mathematische Funktion, welche innerhalb von neuronalen Netzwerken genutzt wird und darüber entscheidet, ob ein Neuron aktiviert wird oder nicht. Dabei verarbeitet sie die gewichtete Summe der Eingaben des Neurons und errechnet daraus einen neuen Wert, um zu bestimmen, wie stark das Signal an die nächste Schicht im Netzwerk weitergegeben wird. In einfachen Worten entscheidet die Aktivierungsfunktion darüber, wie stark die Reaktion des Neurons auf die gewichteten Eingabewerte ausfällt.

Die Aktivierungsfunktion spielt eine entscheidende Rolle beim Training von neuronalen Netzwerken, da sie die Modellierung von nicht-linearen Beziehungen ermöglicht. Die Wahl der geeigneten Funktion für die Modellarchitektur und die zugrundeliegenden Daten hat einen entscheidenden Einfluss auf die schlussendlichen Ergebnisse und ist somit ein wichtiger Bestandteil bei der Erstellung eines neuronalen Netzwerks. 

Welche Eigenschaften haben Aktivierungsfunktionen?

Die Aktivierungsfunktion hat einen wichtigen Einfluss auf die Leistungsfähigkeit von neuronalen Netzwerken und sollte abhängig von der Komplexität der Daten und dem Vorhersagetypen gewählt werden. Obwohl eine Vielzahl an Funktionen zur Auswahl stehen, vereinen doch alle die folgenden Eigenschaften, die wir in diesem Abschnitt genauer erläutern. 

Eine der wichtigsten Eigenschaften von Aktivierungsfunktionen ist deren Nicht-Linearität, welche es ermöglicht, dass die Modelle auch komplexe Zusammenhänge aus den Daten erlernen können, welche über einfache, lineare Beziehungen hinaus gehen. Erst damit lassen sich die herausfordernden Anwendungen in der Bild- oder Sprachverarbeitung meistern. Es können zwar auch nicht-lineare Aktivierungsfunktionen genutzt werden, diese haben jedoch einige Nachteile, wie wir im folgenden Abschnitt sehen werden.

Hinzu kommt, dass alle Aktivierungsfunktionen differenzierbar sein müssen. Man muss also mathematisch in der Lage sein, die Ableitung der Funktion zu bilden, damit der Lernprozess der Neuronalen Netzwerke stattfinden kann. Dieser Prozess basiert auf dem Backpropagation-Algorithmus, bei welchem in jeder Iteration der Gradient, also die Ableitung in mehreren Dimensionen, berechnet wird und anhand der Ergebnisse die Gewichte der einzelnen Neuronen so verändert werden, dass die Vorhersagequalität steigt. Nur durch diesen Prozess und die Differenzierbarkeit der Aktivierungsfunktion ist das Modell in der Lage zu lernen und sich stetig zu verbessern. 

Neben diesen positiven oder zumindest neutralen Eigenschaften besitzen Aktivierungsfunktionen, jedoch auch problematische Eigenschaften, welche zu Herausforderungen während des Trainings führen können. Einige Aktivierungsfunktionen, wie zum Beispiel Sigmoid oder Tanh, haben Sättigungsbereiche, in denen die Gradienten sehr klein werden und nahe Null kommen. Innerhalb dieser Bereiche bewirken Änderungen in den Eingabewerten nur sehr kleine Veränderungen in der Aktivierungsfunktion, sodass sich das Training des Netzwerkes stark verlangsamt. Dieser sogenannte Vanishing Gradient Effekt tritt vor allem in den Wertbereichen auf, in denen die Aktivierungsfunktion an die Minimal- oder Maximalwerte stößt. 

Es ist wichtig, diese zentralen Eigenschaften von Aktivierungsfunktionen zu kennen. 

Welche Aktivierungsfunktionen werden häufig genutzt?

Die Auswahl einer geeigneten Aktivierungsfunktion ist ein zentraler Aspekt für ein erfolgreiches Training eines Machine Learning Modells. Deshalb stellen wir in diesem Abschnitt die am weitesten verbreiteten Funktionen vor, mit denen sich viele Anwendungen umsetzen lassen. Dabei gehen wir auch im Besonderen auf die Unterschiede und Einsatzgebiete ein.  

Lineare Aktivierungsfunktion

Als Ausgangspunkt und zur besseren Vergleichbarkeit mit späteren Funktionen, starten wir mit der denkbar einfachsten Aktivierungsfunktion. Die lineare Aktivierungsfunktion gibt den Eingabewert wieder unverändert heraus und wird durch die folgende Formel beschrieben: 

\(\)\[f(x) = x \]

Obwohl es scheint, als nehme diese Funktion keine Veränderung an den Daten vor, hat sie doch einen wichtigen Einfluss auf die Funktionsweise des Netzwerkes. Sie sorgt nämlich dafür, dass das neuronale Netz ausschließlich lineare Zusammenhänge in den Daten erkennen kann. Dadurch wird die Leistungsfähigkeit immens eingeschränkt, da keine komplexeren Strukturen aus den Daten erlernt werden können. Aus diesem Grund wird diese einfache Aktivierungsfunktion kaum in tiefen neuronalen Netzwerken genutzt, sondern ausschließlich in einfacheren, linearen Modellen oder bei der Outputschicht für Regressionen. 

Sigmoid – Funktion

Die Sigmoid-Funktion ist eine der ältesten nicht-linearen Aktivierungsfunktionen, die bereits seit vielen Jahren im Bereich des Machine Learnings genutzt wird. Sie wird durch die folgende, mathematische Formel beschrieben: 

\(\) \[f(x)\ = \frac{1}{1\ + e^{-x}} \]

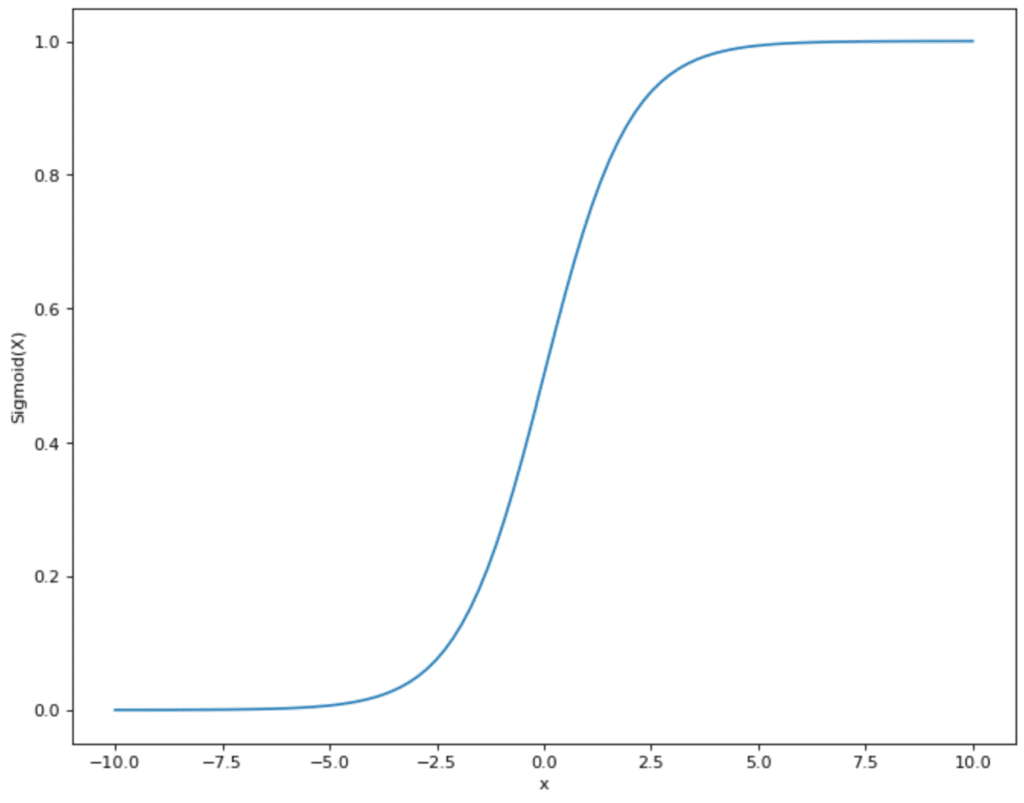
Diese Funktion sorgt dafür, dass der Eingabewert in einen Bereich zwischen 0 und 1 gemappt wird. Dabei folgt der Graph der charakteristischen S-Kurve, welche dafür sorgt, dass kleine Werte in einem Bereich nahe 0 liegen und hohe Werte in einen Bereich nahe 1 transformiert werden. 

Durch diesen Wertebereich bietet sich die Sigmoid-Funktion vor allem für Anwendungen an, in denen binäre Werte vorhergesagt werden sollen, sodass die Ausgabe dann als Wahrscheinlichkeit der Zugehörigkeit interpretiert werden kann. Deshalb wird die Sigmoid-Funktion vor allem in der letzten Schicht eines Netzwerks genutzt, wenn es zu einer binären Vorhersage kommen soll. Das kann zum Beispiel im Bereich der Objekterkennung in Bildern nützlich sein oder bei medizinischen Diagnosen, bei denen eine Patientin als gesund oder krank klassifiziert werden soll. 

Der Hauptnachteil der Sigmoid-Funktion besteht darin, dass das sogenannte Vanishing Gradient Problem auftreten kann. Dabei kann es bei sehr großen oder sehr kleinen Eingabewerten dazu kommen, dass sich der Gradientenwert bei der Ableitung der Null annähert. Dadurch werden dann die Gewichte der Neuronen während der Backpropagation gar nicht oder nur sehr wenig angepasst, wodurch das Training nur langsam vorangeht und ineffizient wird.  

Außerdem kann es zu Problemen führen, dass die Ausgabewerte der Sigmoid-Funktion nicht um die Null zentriert sind, sondern zwischen 0 und 1 liegen. Dadurch liegt sowohl der positive als auch der negative Gradient stets in derselben Richtung, wodurch die Konvergenz des Modells zusätzlich verlangsamt wird. 

Aufgrund dieser Nachteile wird die Sigmoid-Funktion in modernen Netzwerkarchitekturen zunehmend von anderen Aktivierungsfunktionen ersetzt, welche ein effizienteres Training ermöglichen, was vor allem in tiefen Architekturen immens wichtig ist. 

Hyperbolic Tangens (Tanh)

Die hyperbolische Tangens-Funktion, oder auch tanh genannt, ist eine weitere nicht-lineare Aktivierungsfunktion, welche in neuronalen Netzwerken eingesetzt wird, um komplexere Beziehungen in den Daten zu erlernen. Sie beruht auf der folgenden, mathematischen Formel: 

\(\) \[f\left(x\right)=tanh\left(x\right)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \]

Die tanh-Funktion transformiert den Eingabewert in den Bereich zwischen -1 und 1, im Gegensatz zu Sigmoid sind die Werte dadurch um die Null verteilt. Dadurch ergeben sich einige Vorteile im Vergleich zu den bisher vorgestellten Aktivierungsfunktionen, da die Zentrierung um Null hilft, den Trainingseffekt zu verbessern und die Gewichtsanpassungen bewegen sich dadurch schneller in die richtige Richtung. 

Außerdem ist es vorteilhaft, dass die tanh-Funktion auch kleinere Eingabewerte stärker im Ausgabebereich skaliert, sodass die Werte besser voneinander getrennt werden können, vor allem denn, wenn der Eingabebereich nahe beieinander liegt. 

Aufgrund dieser Eigenschaften wird der Hyperbolic Tangens häufig in Recurrent Neural Networks eingesetzt, bei denen zeitliche Sequenzen und Abhängigkeiten eine wichtige Rolle spielen. Durch die Nutzung von positiven und negativen Werten können die Zustandsänderungen in einem RNN deutlich präziser dargestellt werden. 

Im Vergleich zur Sigmoid-Funktion kämpft auch der Hyperbolic Tangens mit denselben Problemen. Das Vanishing Gradient Problem kann auch bei dieser Aktivierungsfunktion auftreten, vor allem bei extrem großen oder kleinen Werten. Bei sehr tiefen neuronalen Netzwerken wird es dann schwierig, die Gradienten im vorderen Teil des Netzes stark genug zu halten, um ausreichende Gewichtsanpassungen vornehmen zu können. Außerdem kann es in diesen Wertebereichen auch zu Sättigungseffekten kommen, sodass der Gradient nahe der 1 oder -1 stark abflacht. 

Rectified Linear Unit (ReLU)

Die Rectified Linear Unit (kurz: ReLU) ist eine lineare Aktivierungsfunktion, die zur Lösung des Vanishing Gradient Problems eingeführt wurde und in den letzten Jahren in der Anwendung immer populärer wurde. Kurz gesagt, behält sie positive Werte und setzt negative Eingabewerte gleich null. Mathematisch ausgedrückt wird dies durch die folgende Bezeichnung:

\(\) \[ f(x)\ =\ \begin{cases}\ x\ &\ {if\ x\ \geq\ 0}\\ 0\ &\ {if\ x\ <\ 0}\ \end{cases} \]

Einfacher geschrieben, kann sie mithilfe der Max-Funktion dargestellt werden: 

\(\) \[f(x) = \max(x,0) \]

Die ReLU Aktivierungsfunktion hat sich vor allem aufgrund der folgenden Vorteile durchgesetzt: 

• Einfache Berechnung: Im Vergleich zu den anderen Optionen lässt sich die ReLU Funktion sehr einfach berechnen und spart so vor allem bei großen Netzwerken viel Rechenleistung. Dies schlägt sich entweder in niedrigeren Kosten oder einer niedrigeren Trainingszeit nieder. 
• Kein Vanishing Gradient Problem: Durch den linearen Aufbau gibt es die asymptotischen Stellen, die parallel zur x-Achse sind, nicht. Dadurch wird der Gradient nicht verschwindend gering und der Fehler durchläuft auch bei großen Netzwerken alle Schichten. Schließlich wird sichergestellt, dass das Netzwerk auch wirklich Strukturen erlernt und der Lernprozess deutlich beschleunigt wird. 
• Bessere Ergebnisse für neue Modellarchitekturen: Im Vergleich zu den anderen Aktivierungsfunktionen kann ReLU Werte gleich Null setzen, nämlich sobald sie negativ sind. Bei der Sigmoid, Softmax und tanh Funktion hingegen nähern sich die Werte nur asymptotisch der Null an, werden jedoch nie gleich Null. Dies führt jedoch in neueren Modellen, wie beispielsweise bei Autoencoders, zu Problemen, da in der sogenannten Code-Schicht echte Nullen benötigt werden, um gute Ergebnisse erzielen zu können. 
• Sparsamkeit: Durch die Fähigkeit der Aktivierungsfunktion, gewisse Eingabewerte auf Null setzen zu können, geht das Modell deutlich sparsamer mit der Rechenleistung ab. Wenn Neuronen dauerhaft Nullwerte erhalten, “sterben” diese ab und werden inaktiv. Dadurch wird die Komplexität des Modells reduziert und es kann zu einer besseren Generalisierung kommen. 

Jedoch gibt es mit dieser einfachen Aktivierungsfunktion auch Probleme. Dadurch, dass negative Werte konsequent gleich Null gesetzt werden, kann es passieren, dass einzelne Neuronen auch eine Gewichtung gleich Null haben, da sie keinerlei Beitrag zum Lernprozess liefern und somit “absterben”. Bei einzelnen Neuronen mag das erstmal kein Problem sein, es zeigt sich jedoch, dass teilweise sogar 20 – 50 % der Neuronen durch ReLU “absterben” können.

Dieses Problem tritt vermehrt auf, wenn eine zu hohe Lernrate definiert wurde, sodass die Gewichte des Neurons sich so verändern können, dass das Neuron nur noch negative Werte erhält. Langfristig bleiben diese Neuronen dann auch tot, weil sie keinen Gradienten mehr erzeugen und auch nicht mehr lernfähig sind. Dadurch sind Modelle mit ReLU als Aktivierungsfunktion auch hochgradig abhängig von einer gut gewählten Lernrate und sie sollte im Vorhinein sehr gut überlegt sein. 

Darüber hinaus ist es problematisch, dass die ReLU Funktion nicht beschränkt ist und theoretisch unendlich große, positive Werte annehmen kann. Insbesondere in Anwendungen in denen der Ausgabebereich beschränkt ist, wie beispielsweise bei der Vorhersage von Wahrscheinlichkeiten, muss die ReLU-Funktion dann noch mit einer weiteren Aktivierungsfunktion wie dem Softmax ergänzt werden, sodass interpretierbare Ergebnisse ausgegeben werden. 

Die ReLU-Funktion findet vor allem in tiefen Neuronalen Netzen Anwendungen, da die Konvergenz aufgrund der effizienten Gradientenverarbeitung deutlich beschleunigt werden kann. Außerdem kann Rechenaufwand gespart werden, sodass sich die Effizienz des gesamten Modells erhöht. Eine zentrale Anwendung hierbei ist das Training von Autoencodern, das genutzt wird, um komprimierte Repräsentationen der Daten zu erlernen. Durch die sparsamen Aktivierungen kann eine effiziente und komprimierte Darstellung gefunden werden.  

Leaky ReLU

Um diesen Nachteil zu beheben und die ReLU Funktion robuster zu machen, hat sich eine Optimierung der Funktion gebildet, die man als Leaky ReLU bezeichnet. Im Vergleich zur herkömmlichen Version der Funktion, werden negative Werte nicht gleich Null gesetzt, sondern ihnen eine (wenn auch kleine) positive Steigung gegeben. Mathematisch sieht das dann wie folgt aus:

\(\) \[ f(x) = \begin{cases} x & \text{if x ≥ 0}\\ \alpha x & \text{if x < 0} \end{cases} \]

Kompakter geschrieben sieht die Funktion, dann wie folgt aus: 

\(\) \[ f(x) = \max(0.01x,\ x) \]

Der Parameter \(\alpha\) ist eine positive Konstante, die vor dem Training bestimmt werden muss und beispielsweise bei 0.01 liegen kann. Dadurch wird gewährleistet, dass selbst, wenn das Neuron negative Werte erhält, es trotzdem nicht Null wird und somit noch einen kleinen Gradienten erzeugen kann. Dies verhindert das Absterben der Neuronen, da sie immer noch einen kleinen Beitrag zum Lernen leisten. 

Neben diesem Vorteil der Leaky ReLU-Funktion, zeichnet sich diese Aktivierungsfunktion auch dadurch aus, dass die Lernfähigkeit des Modells erhöht wird, da die Möglichkeit besteht, auch mit negativen Werten zu lernen und deren Informationen nicht verloren gehen. Diese Eigenschaft kann zu einer schnelleren Konvergenz führen, da mehr Neuronen aktiv bleiben und am Lernprozess teilnehmen. Zusätzlich hat diese Aktivierungsfunktion den Vorteil, dass sie trotz der kleinen Änderugen zur ReLU ähnlich effizient berechnet werden kann. 

Ein möglicher Nachteil ist, dass durch \(\alpha\) ein weiterer Hyperparameter eingeführt wird, welcher vor dem Training bestimmt werden muss und eine großen Einfluss auf die Qualität des Trainings hat. Ein zu kleiner Wert kann das Lernen verlangsamen, da manche Neuronen zwar nicht absterben, aber nahe an Null kommen und dadurdch nur noch wenig zum Training beitragen. 

Softmax

Der Softmax ist eine mathematische Funktion, die einen Vektor als Input nimmt und dessen einzelne Werte in Wahrscheinlichkeiten umwandelt, abhängig von deren Größe. Ein hoher numerischer Wert führt dabei zu einer hohen Wahrscheinlichkeit im resultierenden Vektor.

In Worten gesprochen, wird jeder Wert des Vektors durch die Summe aller Werte des Ausgangsvektors geteilt und im neuen Vektor abgelegt. Rein mathematisch sieht diese Formel dann so aus: 

\(\) \[\sigma (x)_{j} = \frac{e^{z_{j}}}{\sum_{k=1}^{K} e^{z_{k}}} \text{for } j = 1, …, K.\]

Mit einem konkreten Beispiel wird die Funktionsweise der Softmax-Funktion deutlicher: 

\(\) \[\begin{pmatrix}1 \\ 2 \\3 \end{pmatrix} \underrightarrow{Softmax} \begin{pmatrix}\frac{1}{1 + 2 + 3} \\ \frac{2}{1 + 2 + 3} \\ \frac{3}{1 + 2 + 3} \end{pmatrix} = \begin{pmatrix} 0.166 \\ 0.33 \\ 0.5 \end{pmatrix} \]

Das positive Merkmal dieser Funktion ist, dass dafür gesorgt wird, dass die Summe der Ausgabewerte immer kleiner oder gleich 1 sind. Das ist vor allem in der Wahrscheinlichkeitsrechnung sehr von Vorteil, da so gewährleistet ist, dass keine addierte Wahrscheinlichkeit größer 1 herauskommen kann.

Auf den ersten Blick erscheinen die Sigmoid- und die Softmax-Funktion relativ ähnlich, da beide Funktionen den Eingangswert auf den Zahlenbereich zwischen 0 und 1 abbilden. Auch deren Verlauf ist nahezu identisch mit dem Unterschied, dass die Sigmoid-Funktion bei x = 0 den Wert 0,5 durchläuft und die Softmax-Funktion an diesem Punkt noch unterhalb von 0,5 liegt.

Der Unterschied zwischen den Funktionen liegt in der Anwendung. Die Sigmoid-Funktion kann für binäre Klassifikationen genutzt werden, also für Modelle, in denen zwischen zwei unterschiedlichen Klassen entschieden werden soll. Der Softmax hingegen kann auch für Klassifikationen genutzt werden, die mehr als zwei Klassen vorhersagen sollen. Dabei stellt die Funktion sicher, dass die Wahrscheinlichkeit aller Klassen 1 ergibt. 

Die Vorteile des Softmax liegen darin, dass die Ausgaben klar interpretierbar sind und Wahrscheinlichkeiten darstellen, welche besonders in Klassifizierungsproblemen hilfreich sind. Außerdem werden exponentielle Werte verwendet, sodass die Funktion numerisch stabil ist und auch große Differenzen in den Eingabedaten handhaben kann. 

Zu den Nachteilen zählt unter anderem die Overconfidence, welche die Eigenschaft beschreibt, dass die Vorhersagen zu selbstbewusst sind, obwohl sich das Modell ziemlich unsicher ist. Deshalb sollten Maßnahmen zur Unsicherheitsbewertung eingefügt werden, um dieses Problem zu umgehen. Außerdem ist der Softmax zwar für Mehrklassenklassifikationen geeignet, jedoch sollte die Anzahl der Klassen auch nicht zu stark ansteigen, da dann die exponentielle Berechnung für jede Klasse zu aufwändig und rechenintensiv ist. Zusätzlich kann dann der Fall eintreten, dass das Modell instabiler wird, da die Wahrscheinlichkeiten für einzelne Klassen zu niedrig werden.

Wie wählt man die richtige Aktivierungsfunktion?

Die Aktivierungsfunktion ist ein entscheidender Baustein innerhalb eines neuronalen Netzwerkes und hat einen immensen Einfluss auf die Leistungsfähigkeit des Modells. Deshalb ist die Auswahl einer geeigneten Funktion ein wichtiger Schritt bei der Erstellung der Architektur und sollte gut durchdacht werden. Die Wahl sollte vor allem von der Anwendung und der verwendeten Architektur abhängen, da die Aktivierungsfunktionen unterschiedliche Eigenschaften haben, die in verschiedenen Situationen vorteilhaft oder nachteilhaft sein können. 

In den Hidden Layers haben sich die Aktivierungsfunktion ReLU und ihre Varianten etabliert, da sie sehr effizient zu berechnen sind und gleichzeitig das Vanishing Gradient Problem umgehen, was ein wichtiger Faktor in diesem Bereich der Architektur ist. Außerdem handelt es sich um eine nicht-lineare Aktivierungsfunktion, die das Modell in die Lage versetzt auch komplexere Zusammenhänge zu erlernen. Mithilfe von Leaky ReLU kann das Netzwerk zusätzlich das Problem der Dead Neurons vermeiden und ist dadurch in der Lage noch besser zu lernen.

In den Ausgabeschichten hingegen macht es Sinn, die Aktivierungsfunktion an die jeweilige Anwendung anzupassen. Für Klassifizierungsprobleme bieten sich beispielsweise Softmax und Sigmoid an, da sie einen Wahrscheinlichkeitswert der Zugehörigkeit ausgeben. Für Anwendungen mit lediglich zwei Klassen bietet sich die Sigmoid-Funktion an, während bei Mehrklassenproblemen die Softmax-Funktion verwendet wird, welche sicherstellt, dass die Wahrscheinlichkeiten aller Klassen auf 1 summieren. 

Für Ausgabeschichten, welche ein lineares Regressionsproblem abbilden sollen, bieten sich lineare Aktivierungsfunktionen an, da diese keine Begrenzung der Werte vornehmen und deshalb für kontinuierliche Vorhersagen sehr gut geeignet sind. 

Die Wahl der richtigen Aktivierungsfunktion hat einen großen Einfluss auf das Training eines neuronalen Netzwerks. Dabei dominieren die ReLU und ihre Varianten die versteckten Schichten aufgrund ihrer effizienten Berechnung und dem nicht vorhandenen Vanishing Gradient Problem. In der Ausgabeschicht hingegen kommt es auf den konkreten Anwendungsfall an, welche Funktion am besten geeignet ist. 

Das solltest Du mitnehmen

• Neuronale Netze bestehen aus sogenannten Perceptrons oder einzelne Neuronen, welche aus verschiedenen Inputs einen oder mehrere Outputs generieren. 
• Die Aktivierungsfunktion eines Neurons bestimmt darüber, wie stark ein Neuron von den konkreten Eingabewerten aktiviert wird. 
• Zu den charakterisierenden Eigenschaften von Aktivierungsfunktionen zählt, ob sie linear oder nicht-linear sind, dass sie differenzierbar sein müssen und ob sie Sättigungsbereiche besitzen, in denen es zum Vanishing Gradient Problem kommen kann. 
• In der Anwendung haben sich verschiedene Aktivierungsfunktionen durchgesetzt, wie zum Beispiel die Softmax-Funktion, der Sigmoid, die Rectified Linear Unit oder der Leaky ReLU. 
• Die Wahl der richtigen Aktivierungsfunktion hängt vor allem von der Architektur des Netzwerks und der Anwendung ab. 

Andere Beiträge zum Thema Aktivierungsfunktionen

• Hier findest Du einen Überblick über die Aktivierungsfunktionen in TensorFlow.