Neural networks have become a powerful method in machine learning models in recent years. The activation function is a central component in every neural network, which significantly influences the model’s functionality. It determines how strongly a neuron in the network is activated and thus decides which structures are learned from the data. Without the activation functions, the neural networks could only recognize linear relationships and would not be able to produce the impressive results that have kept us in suspense in recent years.

In this article, we look in detail at the properties of an activation function and compare the different functions that are commonly used. We also provide tips on how to find the right activation function for the network architecture and the specific use case to train an optimal model. However, before we can dive into the topic, we should understand how neural networks and more specifically the neurons in them work to see in which system the activation function is embedded.

How does a Perceptron work?

The perceptron is originally a mathematical model and was only later used in computer science and machine learning due to its ability to learn complex relationships. In its simplest form, it consists of exactly one neuron, which mimics the structure of the human brain.

The perceptron has several inputs at which it receives numerical information, i.e. numerical values. The number of inputs can vary depending on the application. The inputs have different weights, which indicate how influential the inputs are for the final output. During the learning process, the weights are changed to produce the best possible results.

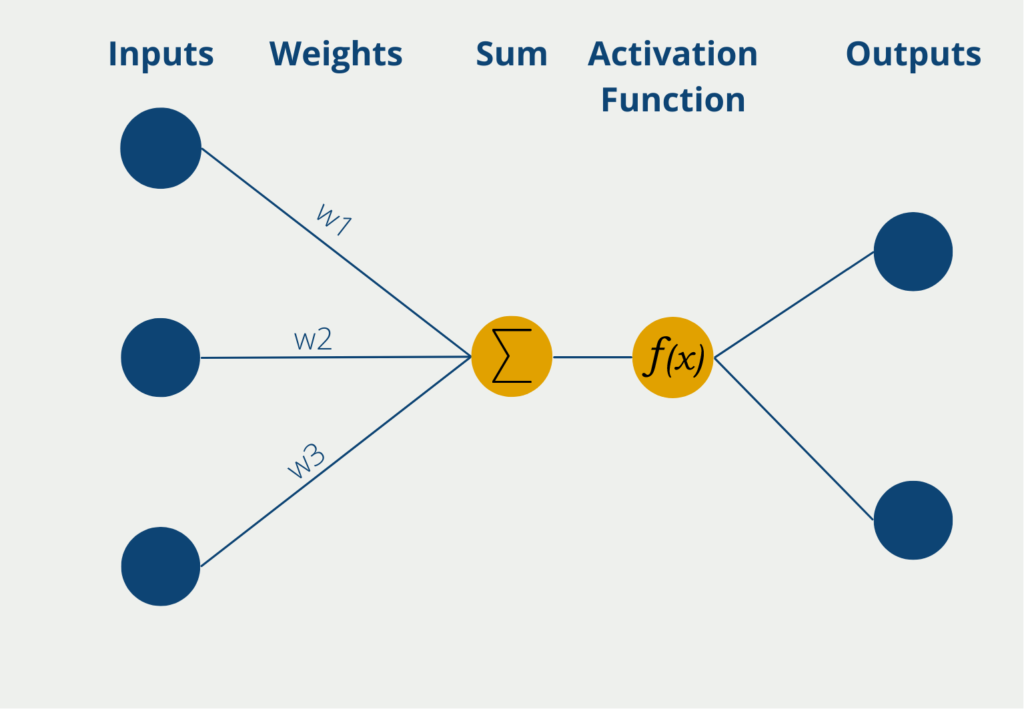
The neuron itself then forms the sum of the input values multiplied by the weights of the inputs. This weighted sum is passed on to the so-called activation function, which contains the logic that is learned in the model. In its simplest form, the neuron only has one output, which can assume binary values such as “yes/no” or “active/inactive”. The activation function then has the corresponding property of mapping continuous values to 0 or 1. The output is then the prediction of the perceptron.

A neural network consists of millions or even billions of such neurons, which are then organized in different layers. This structure enables them to recognize and learn even more complex relationships in the data.

As an example of how a perceptron works, let’s take a closer look at the work of a politician. She is a member of parliament and a new law has to be voted on. The politician must therefore decide whether to approve or reject the proposed law (abstention is not possible in our example). The perceptron therefore has a binary output, namely approval or rejection.

Various sources of information are available to the politician as input for her decision. On the one hand, there is an information paper with background information issued by parliament. Furthermore, the MP can find out about various issues on the Internet or discuss them with other colleagues. The politician weights her input, i.e. her sources of information, according to how trustworthy she considers them to be. For example, she assigns less weight to the parliamentary information paper, as she fears that the research is not detailed enough and should already lean in a certain direction. It then takes the sum of the information available to it, together with the weightings, and passes it on to the activation function.

We can think of this as the politician’s head, which uses the inputs to decide whether or not to approve the proposed legislation. Even minor details in the inputs can lead to a massive change in the politician’s opinion.

What is an Activation Function?

The activation function is a mathematical function that is used within neural networks and decides whether a neuron is activated or not. It processes the weighted sum of the neuron’s inputs and calculates a new value to determine how strongly the signal is passed on to the next layer in the network. In simple terms, the activation function determines the strength of the neuron’s response to the weighted input values.

The activation function plays a crucial role in the training of neural networks, as it enables the modeling of non-linear relationships. The choice of the appropriate function for the model architecture and the underlying data has a decisive influence on the final results and is therefore an important component in the creation of a neural network.

What Properties do Activation Functions have?

The activation function has an important influence on the performance of neural networks and should be chosen depending on the complexity of the data and the prediction type. Although there are a variety of functions to choose from, they all share the following properties, which we explain in more detail in this section.

One of the most important properties of activation functions is their non-linearity, which enables the models to learn complex relationships from the data that go beyond simple, linear relationships. Only then can the challenging applications in image or speech processing be mastered. Although non-linear activation functions can also be used, these have some disadvantages, as we will see in the following section.

In addition, all activation functions must be differentiable. In other words, it must be mathematically possible to form the derivative of the function so that the learning process of the neural networks can take place. This process is based on the backpropagation algorithm, in which the gradient, i.e. the derivative in several dimensions, is calculated in each iteration and the weights of the individual neurons are changed based on the results so that the prediction quality increases. Only through this process and the differentiability of the activation function is the model able to learn and continuously improve.

In addition to these positive or at least neutral properties, activation functions also have problematic properties that can lead to challenges during training. Some activation functions, such as Sigmoid or Tanh, have saturation regions in which the gradients become very small and come close to zero. Within these ranges, changes in the input values cause only very small changes in the activation function, so that the training of the network slows down considerably. This so-called vanishing gradient effect occurs above all in the value ranges in which the activation function reaches the minimum or maximum values.

It is important to know these central properties of activation functions.

Which Activation Functions are frequently used?

The selection of a suitable activation function is a key aspect of the successful training of a machine learning model. In this section, we therefore present the most widely used functions that can be used to implement many applications. We will also go into the differences and areas of application in particular.

Linear activation function

As a starting point and for better comparability with later functions, we start with the simplest possible activation function. The linear activation function returns the input value unchanged and is described by the following formula:

\(\)\[f(x) = x \]

Although it appears that this function does not make any changes to the data, it does have an important influence on how the network functions. It ensures that the neural network can only recognize linear relationships in the data. This limits its performance immensely, as no more complex structures can be learned from the data. For this reason, this simple activation function is rarely used in deep neural networks, but only in simpler, linear models or in the output layer for regressions.

Sigmoid function

The sigmoid function is one of the oldest non-linear activation functions that has been used in the field of machine learning for many years. It is described by the following mathematical formula:

\(\) \[f(x)\ = \frac{1}{1\ + e^{-x}} \]

This function ensures that the input value is mapped to a range between 0 and 1. The graph follows the characteristic S-curve, which ensures that small values lie in a range close to 0 and high values are transformed into a range close to 1.

This range of values makes the sigmoid function particularly suitable for applications in which binary values are to be predicted so that the output can then be interpreted as the probability of membership. For this reason, the sigmoid function is primarily used in the last layer of a network if a binary prediction is to be made. This can be useful, for example, in the area of object recognition in images or in medical diagnoses where a patient is to be classified as healthy or ill.

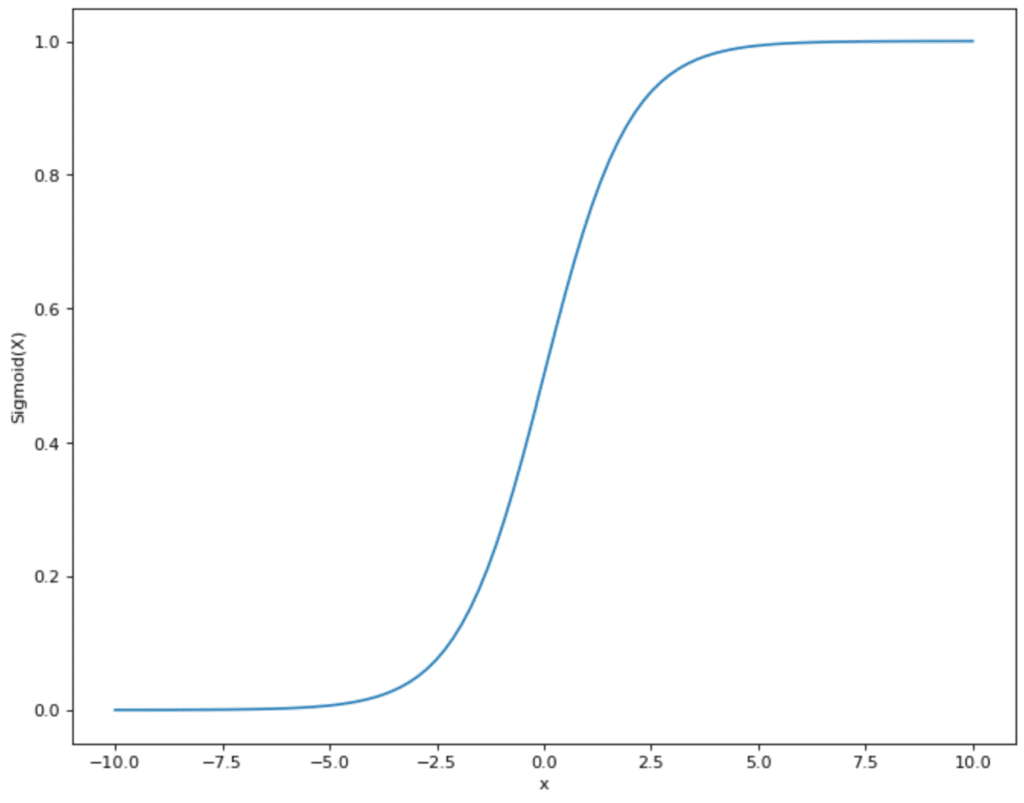
The main disadvantage of the sigmoid function is that the so-called vanishing gradient problem can occur. With very large or very small input values, the gradient value may approach zero during derivation. As a result, the weights of the neurons are not adjusted at all or only very slightly during backpropagation, making training slow and inefficient.

It can also lead to problems if the output values of the sigmoid function are not centered around zero, but lie between 0 and 1. This means that both the positive and negative gradients are always in the same direction, which further slows down the convergence of the model.

Due to these disadvantages, the sigmoid function is increasingly being replaced in modern network architectures by other activation functions that enable more efficient training, which is particularly important in deep architectures.

Hyperbolic tangent (Tanh)

The hyperbolic tangent function, or tanh, is another non-linear activation function used in neural networks to learn more complex relationships in the data. It is based on the following mathematical formula:

\(\) \[f\left(x\right)=tanh\left(x\right)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \]

The tanh function transforms the input value into the range between -1 and 1. In contrast to Sigmoid, the values are therefore distributed around zero. This results in some advantages compared to the previously presented activation functions, as the centering around zero helps to improve the training effect and the weight adjustments move faster in the right direction.

It is also advantageous that the tanh function also scales smaller input values more strongly in the output range so that the values can be better separated from each other, especially when the input range is close together.

Due to these properties, the hyperbolic tangent is often used in recurrent neural networks where temporal sequences and dependencies play an important role. By using positive and negative values, the state changes in an RNN can be represented much more precisely.

Compared to the sigmoid function, the hyperbolic tangent also struggles with the same problems. The vanishing gradient problem can also occur with this activation function, especially with extremely large or small values. With very deep neural networks, it then becomes difficult to keep the gradients in the front part of the network strong enough to make sufficient weight adjustments. In addition, saturation effects can also occur in these value ranges, so that the gradient decreases sharply near 1 or -1.

Rectified Linear Unit (ReLU)

The Rectified Linear Unit (ReLU for short) is a linear activation function that was introduced to solve the vanishing gradient problem and has become increasingly popular in recent years. In short, it keeps positive values and sets negative input values equal to zero. Mathematically, this is expressed by the following term:

\(\) \[ f(x)\ =\ \begin{cases}\ x\ &\ {if\ x\ \geq\ 0}\\ 0\ &\ {if\ x\ <\ 0}\ \end{cases} \]

In simpler terms, it can be represented using the max function:

\(\) \[f(x) = \max(x,0) \]

The ReLU activation function has established itself primarily due to the following advantages:

• Simple calculation: Compared to the other options, the ReLU function is very easy to calculate and therefore saves a lot of computing power, especially for large networks. This is reflected either in lower costs or a shorter training time.
• No vanishing gradient problem: Due to the linear structure, there are no asymptotic points that are parallel to the x-axis. This means that the gradient is not vanishingly small and the error runs through all layers, even with large networks. Finally, it is ensured that the network actually learns structures and the learning process is significantly accelerated.
• Better results for new model architectures: Compared to the other activation functions, ReLU can set values to zero as soon as they are negative. With the sigmoid, softmax, and tanh functions, on the other hand, the values only approach zero asymptotically, but never become zero. However, this leads to problems in newer models, such as autoencoders, as real zeros are required in the so-called code layer in order to achieve good results.
• Economy: The ability of the activation function to set certain input values to zero makes the model much more economical with computing power. If neurons are permanently given zero values, they “die” and become inactive. This reduces the complexity of the model and can lead to better generalization.

However, there are also problems with this simple activation function. Because negative values are consistently set to zero, it can happen that individual neurons also have a weighting of zero, as they make no contribution to the learning process and therefore “die off”. This may not initially be a problem for individual neurons, but it has been shown that in some cases as many as 20 – 50 % of neurons can “die off” as a result of ReLU.

This problem occurs more frequently if too high a learning rate has been defined so that the weights of the neuron can change in such a way that the neuron only receives negative values. In the long term, these neurons remain dead because they no longer generate a gradient and are no longer capable of learning. This means that models with ReLU as an activation function are also highly dependent on a well-chosen learning rate, which should be carefully considered in advance.

Furthermore, it is problematic that the ReLU function is not limited and can theoretically assume infinitely large, positive values. Particularly in applications where the output range is limited, such as the prediction of probabilities, the ReLU function must then be supplemented with another activation function such as the softmax so that interpretable results are output.

The ReLU function is primarily used in deep neural networks, as convergence can be significantly accelerated due to efficient gradient processing. In addition, computational effort can be saved, increasing the efficiency of the entire model. A central application here is the training of autoencoders, which is used to learn compressed representations of the data. An efficient and compressed representation can be found through the sparse activations.

Leaky ReLU

To eliminate this disadvantage and make the ReLU function more robust, an optimization of the function has been developed, which is known as Leaky ReLU. Compared to the conventional version of the function, negative values are not set to zero but are given an (albeit small) positive slope. Mathematically, this looks like this:

\(\) \[ f(x) = \begin{cases} x & \text{if x ≥ 0}\\ \alpha x & \text{if x < 0} \end{cases} \]

In more compact form, the function looks like this:

\(\) \[ f(x) = \max(0.01x,\ x) \]

The parameter \(\alpha\) is a positive constant that must be determined before training and can be 0.01, for example. This ensures that even if the neuron receives negative values, it still does not become zero and can therefore still generate a small gradient. This prevents the neurons from dying, as they still make a small contribution to learning.

In addition to this advantage of the Leaky ReLU function, this activation function is also characterized by the fact that the learning ability of the model is increased, as it is possible to learn even with negative values and their information is not lost. This property can lead to faster convergence, as more neurons remain active and participate in the learning process. In addition, this activation function has the advantage that it can be calculated with similar efficiency despite the small changes to the ReLU.

A possible disadvantage is that \(\alpha\) introduces another hyperparameter, which must be determined before training and has a major influence on the quality of the training. A value that is too small can slow down learning, as some neurons do not die, but come close to zero and therefore contribute little to training.

Softmax

The softmax is a mathematical function that takes a vector as input and converts its values into probabilities, depending on their size. A high numerical value leads to a high probability in the resulting vector.

In other words, each value of the vector is divided by the sum of all values of the output vector and stored in the new vector. In purely mathematical terms, this formula looks like this:

\(\) \[\sigma (x)_{j} = \frac{e^{z_{j}}}{\sum_{k=1}^{K} e^{z_{k}}} \text{for } j = 1, …, K.\]

A specific example illustrates how the Softmax function works:

\(\) \[\begin{pmatrix}1 \\ 2 \\3 \end{pmatrix} \underrightarrow{Softmax} \begin{pmatrix}\frac{1}{1 + 2 + 3} \\ \frac{2}{1 + 2 + 3} \\ \frac{3}{1 + 2 + 3} \end{pmatrix} = \begin{pmatrix} 0.166 \\ 0.33 \\ 0.5 \end{pmatrix} \]

The positive feature of this function is that it ensures that the sum of the output values is always less than or equal to 1. This is particularly advantageous in probability calculations, as it ensures that no summed probability can be greater than 1.

At first glance, the sigmoid and softmax functions appear relatively similar, as both functions map the input value to the numerical range between 0 and 1. Their progression is also almost identical with the difference that the sigmoid function passes through the value 0.5 at x = 0 and the softmax function is still below 0.5 at this point.

The difference between the functions lies in the application. The sigmoid function can be used for binary classifications, i.e. for models in which a decision is to be made between two different classes. Softmax, on the other hand, can also be used for classifications that are to predict more than two classes. The function ensures that the probability of all classes is 1.

The advantages of Softmax are that the outputs are interpretable and represent probabilities, which are particularly helpful in classification problems. In addition, exponential values are used so that the function is numerically stable and can also handle large differences in the input data.

Disadvantages include overconfidence, which describes the property that the predictions are overconfident even though the model is quite uncertain. Therefore, measures for uncertainty assessment should be included to avoid this problem. Furthermore, although Softmax is suitable for multi-class classifications, the number of classes should not increase too much, as the exponential calculation for each class would then be too time-consuming and computationally intensive. In addition, the model may then become unstable as the probabilities for individual classes become too low.

How do you choose the right Activation Function?

The activation function is a crucial building block within a neural network and has an immense influence on the performance of the model. Therefore, the selection of a suitable function is an important step in the creation of the architecture and should be well thought out. The choice should depend primarily on the application and the architecture used, as the activation functions have different properties that can be advantageous or disadvantageous in different situations.

In the hidden layers, the activation function ReLU and its variants have established themselves as they are very efficient to calculate and at the same time avoid the vanishing gradient problem, which is an important factor in this area of architecture. It is also a non-linear activation function, which enables the model to learn more complex relationships. With the help of Leaky ReLU, the network can also avoid the problem of dead neurons and is therefore able to learn even better.

In the output layers, on the other hand, it makes sense to adapt the activation function to the respective application. Softmax and Sigmoid, for example, are suitable for classification problems, as they output a probability value of membership. The Sigmoid function is suitable for applications with only two classes, while the Softmax function is used for multi-class problems, which ensures that the probabilities of all classes add up to 1.

Linear activation functions are suitable for output layers that are to map a linear regression problem, as they do not limit the values and are therefore very well suited for continuous predictions.

The choice of the right activation function has a major influence on the training of a neural network. The ReLU and its variants dominate the hidden layers due to their efficient calculation and the non-existent vanishing gradient problem. In the output layer, on the other hand, it depends on the specific use case which function is most suitable.

This is what you should take with you

• Neural networks consist of so-called perceptrons or individual neurons, which generate one or more outputs from various inputs.
• The activation function of a neuron determines how strongly a neuron is activated by the specific input values.
• The characterizing properties of activation functions include whether they are linear or non-linear, whether they must be differentiable, and whether they have saturation regions in which the vanishing gradient problem can occur.
• Various activation functions have become established in the application, such as the softmax function, the sigmoid, the rectified linear unit, or the leaky ReLU.
• The choice of the right activation function depends primarily on the architecture of the network and the application.

Other Articles on the Topic of Activation Function

• Here you can find an overview of the Activation Functions in TensorFlow.