Was ist die ReLU-Funktion (Rectified Linear Unit)?

Die Rectified Linear Unit (ReLU) Aktivierungsfunktion ist eine spezielle Funktion, die zum Training von Neuronalen Netzwerken genutzt wird und sich in die letzten Jahren etabliert hat. Kurz gesagt ist sie eine lineare Funktion, die positive Werte erhält und negative Werte auf Null setzt.

Was ist eine Aktivierungsfunktion?

Die Aktivierungsfunktion kommt in den Neuronen eines Neuronalen Netzwerks vor und wird auf die gewichtete Summe aus Inputwerten des Neurons angewandt. Dadurch, dass die Aktivierungsfunktion nicht linear ist, kann auch das Perceptron nicht-lineare Zusammenhänge erlernen.

Somit erhalten die Neuronalen Netze erst die Eigenschaft auch komplexe Zusammenhänge erlernen und abbilden zu können. Ohne die nicht-lineare Funktion könnten nämlich nur lineare Abhängigkeiten zwischen den gewichteten Inputwerten und den Outputwerten hergestellt werden. Dann könnte man jedoch auch gleich eine Lineare Regression nutzen. Die Abläufe innerhalb eines Perceptrons werden dabei im Folgenden kurz beschrieben.

Das Perceptron hat mehrere Eingänge, die sogenannten Inputs, an denen es numerische Informationen, also Zahlenwerte erhält. Je nach Anwendung kann sich die Zahl der Inputs unterscheiden. Die Eingaben haben verschiedene Gewichte, die angeben, wie einflussreich die Inputs für die schlussendliche Ausgabe sind. Während des Lernprozesses werden die Gewichte so geändert, dass möglichst gute Ergebnisse entstehen.

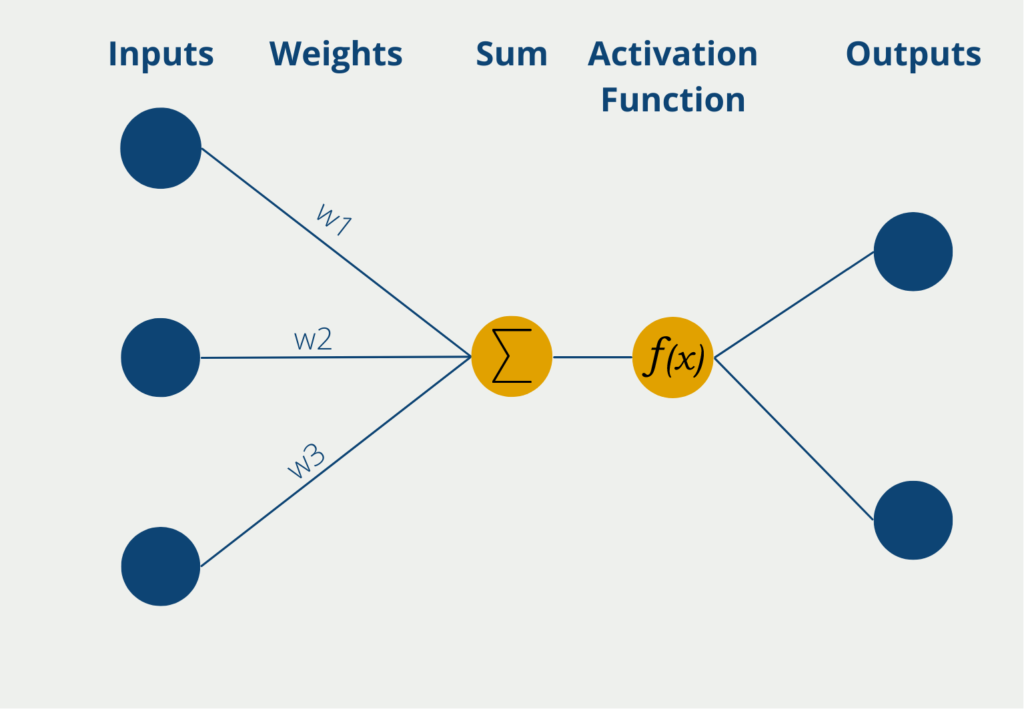
Aufbau eines Perceptrons | Quelle: Autor

Das Neuron selbst bildet dann die Summe der Inputwerte multipliziert mit den Gewichten der Inputs. Diese gewichtete Summe wird weitergeleitet an die sogenannte Aktivierungsfunktion. In der einfachsten Form eines Neurons gibt es genau zwei Ausgaben, es können also nur binäre Outputs vorhergesagt werden, beispielsweise “Ja” oder “Nein” oder “Aktiv” oder “Inaktiv” etc.

Wenn das Neuron binäre Ausgabewerte hat, wird eine Aktivierungsfunktion genutzt, deren Werte auch zwischen 0 und 1 liegen. Somit ergeben sich dann die Ausgabewerte direkt durch die Nutzung der Funktion.

Welche Aktivierungsfunktionen gibt es?

Es gibt viele verschiedene Aktivierungsfunktionen, die im Bereich des Machine Learnings zum Einsatz kommen. Zu den häufigsten zählen:

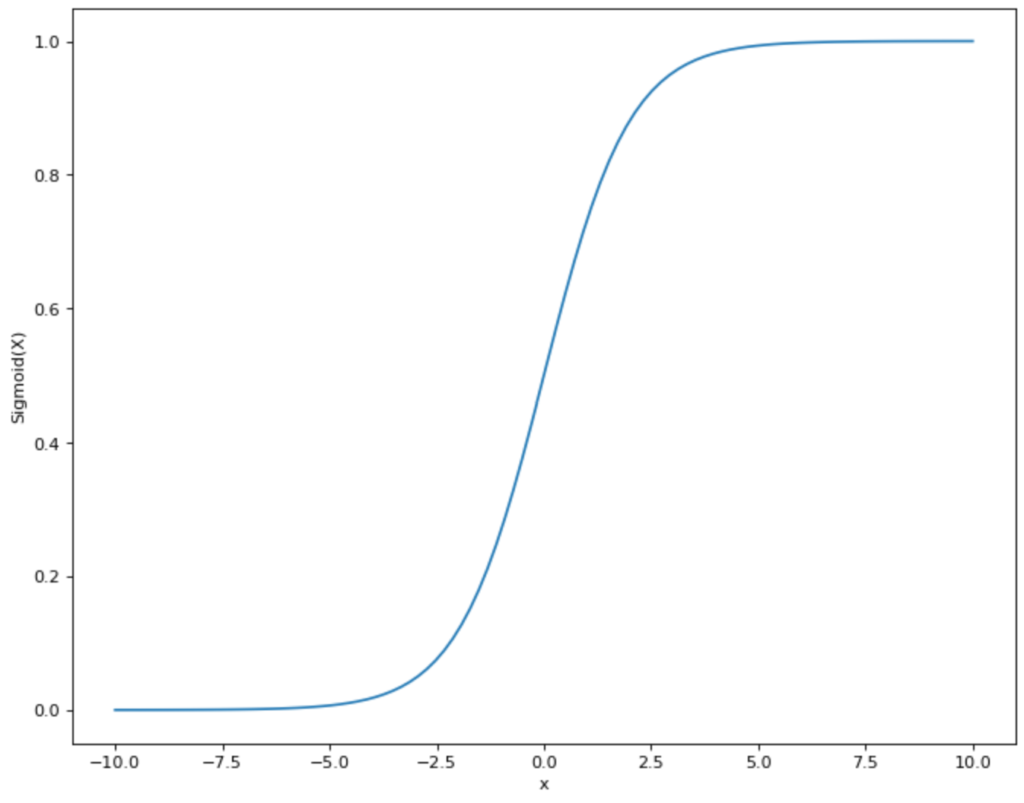
Sigmoid-Funktion: Diese Funktion bildet die Eingangswerte auf den Bereich zwischen 0 und 1 ab.
Tanh-Funktion: Die Tanh-Funktion, oder Tangens – Hyperbolicus ausgeschrieben, mappt die Eingangswerte auf den Bereich zwischen -1 und 1.
Softmax-Funktion: Die Softmax-Funktion bildet die Eingangswerte auch auf den Bereich zwischen 0 und 1 ab, ist aber besonders geeignet für die letzte Schicht im Neuronalen Netzwerk, um dort eine Wahrscheinlichkeitsverteilung darzustellen.

Welche Probleme gibt es mit diesen Aktivierungsfunktionen?

Alle genannten Funktionen sind sogenannte nicht-lineare Aktivierungsfunktionen, das heißt, dass sie nicht proportional zu der x-Variablen verlaufen. Konkret bedeutet dies, dass eine Steigerung von x um eins nicht unbedingt eine Steigerung von y um eins zu bedeuten hat.

Verlauf der Sigmoid Funktion | Quelle: Autor

Diese nicht-linearen Funktionen bieten den Vorteil, dass sie auch komplexe Zusammenhänge zwischen den Eingabe- und den Ausgabevariablen erkennen und erlernen können. Jedoch haben diese Funktionen aufgrund ihres Verlaufs die folgenden Probleme:

Vanishing Gradient / Saturation: Wie wir aus dem Verlauf der Sigmoid-Funktion erkennen können, verläuft die Funktion für sehr große und sehr kleine x-Werte nahezu parallel zur x-Achse. Die Ableitung bzw. der Gradient ist an diesen Stellen nahezu null, da die Funktion keine wirkliche Steigung an diesen Stellen hat. Das führt jedoch bei der sogenannten Backpropagation, also dem Lernprozess des Netzwerks, dazu, dass bei großen und kleinen x-Werten nahezu kein Lerneffekt stattfindet, da der Gradient eigentlich null ist.
Nicht null-zentriert: Sowohl die Sigmoid- als auch die Softmax-Funktion bewegen sich zwischen den y-Werten 0 und 1 und sind somit nicht null-zentriert, das heißt ihr Mittelwert liegt nicht bei 0. Im Lernprozess kann dies problematisch werden, da die Gewichtungen dann immer dasselbe Vorzeichen haben, nämlich entweder alle positiv oder alle negativ. Dies kann unter Umständen zu einem sprunghaften Lernprozess führen. Dieses Problem lässt sich jedoch entgegenwirken, indem man eine Normalisierung vornimmt und somit die Eingabedaten null-zentriert.

Was ist die Rectified Linear Unit (ReLU) Aktivierungsfunktion?

Die Rectified Linear Unit (kurz: ReLU) ist eine lineare Aktivierungsfunktion, die zur Lösung des Vanishing Gradient Problems eingeführt wurde und in den letzten Jahren in der Anwendung immer populärer wurde. Kurz gesagt, behält sie positive Werte und setzt negative Eingabewerte gleich null. Mathematisch ausgedrückt wird dies durch die folgende Bezeichnung:

\(\) \[ f(x) = \begin{cases}
x & \text{if x ≥ 0}\\
0 & \text{if x < 0}
\end{cases} \]

Welche Vor- und Nachteile bietet diese Funktion?

Die ReLU Aktivierungsfunktion hat sich vor allem aufgrund der folgenden Vorteile durchgesetzt:

Einfache Berechnung: Im Vergleich zu den anderen Optionen lässt sich die ReLU Funktion sehr einfach berechnen und spart so vor allem bei großen Netzwerken viel Rechenleistung. Dies schlägt sich entweder in niedrigeren Kosten oder einer niedrigeren Trainingszeit nieder.
Kein Vanishing Gradient Problem: Durch den linearen Aufbau gibt es die asymptotischen Stellen, die parallel zur x-Achse sind nicht. Dadurch wird der Gradient nicht verschwindend gering und der Fehler durchläuft auch bei großen Netzwerken alle Schichten. Dadurch wird sichergestellt, dass das Netzwerk auch wirklich Strukturen erlernt und der Lernprozess deutlich beschleunigt wird.
Bessere Ergebnisse für neue Modellarchitekturen: Im Vergleich zu den anderen Aktivierungsfunktionen kann ReLU Werte gleich Null setzen, nämlich sobald sie negativ sind. Bei der Sigmoid, Softmax und tanh Funktion hingegen nähern sich die Werte nur asymptotisch der Null an, werden jedoch nie gleich Null. Dies führt jedoch in neueren Modellen, wie beispielsweise Autoencoders bei der Erstellung von Deepfakes, zu Problemen, da in der sogenannten Code-Schicht echte Nullen benötigt werden, um gute Ergebnisse erzielen zu können.

Jedoch gibt es mit dieser einfachen Aktivierungsfunktion auch Probleme. Dadurch, dass negative Werte konsequent gleich Null gesetzt werden, kann es passieren, dass einzelne Neuronen auch eine Gewichtung gleich Null haben, da sie keinerlei Beitrag zum Lernprozess liefern und somit “absterben”. Bei einzelnen Neuronen mag das erstmal kein Problem sein, es zeigt sich jedoch, dass teilweise sogar 20 – 50 % der Neuronen durch ReLU “absterben” können.

Was ist die Leaky ReLU Funktion?

Um diesen Nachteil zu beheben und die ReLU Funktion dadurch robuster zu machen, hat sich eine Optimierung der Funktion gebildet, die man als Leaky ReLU bezeichnet. Im Vergleich zur herkömmlichen Version der Funktion, werden negative Werte nicht gleich Null gesetzt, sondern ihnen eine (wenn auch kleine) positive Steigung gegeben. Mathematisch sieht das dann wie folgt aus:

\(\) \[ f(x) = \begin{cases}
x & \text{if x ≥ 0}\\
\alpha x & \text{if x < 0}
\end{cases} \]

Der Parameter α ist eine positive Konstante, die vor dem Training bestimmt werden muss und somit keinen Hyperparameter darstellt, der während dem Training verändert wird. Sie stellt sicher, dass die negativen Werte nicht den Wert Null annehmen können und verhindert somit das “Absterben” von Neuronen.

Welche Anwendungen nutzen die ReLU Aktivierungsfunktion?

Die Funktion der gleichgerichteten linearen Einheit (ReLU) ist eine häufig verwendete Aktivierungsfunktion beim Deep Learning. Sie hat mehrere Anwendungen in verschiedenen Bereichen, darunter:

Computer Vision: ReLU wird häufig in faltbaren neuronalen Netzen (CNNs) für Aufgaben wie Bildklassifizierung, Objekterkennung und Segmentierung verwendet. Diese Modelle haben ansonsten eine hohe Gefahr dafür, dass ganze Neuronen aus dem Modell fallen.
Verarbeitung natürlicher Sprache: ReLU wird in rekurrenten neuronalen Netzen (RNNs) für Aufgaben wie Stimmungsanalyse, maschinelle Übersetzung und Textklassifizierung verwendet.
Empfehlungssysteme: ReLU wird in auf Deep Learning basierenden Empfehlungssystemen verwendet, um die Interaktionsmuster zwischen Benutzer und Artikel aus großen Datensätzen zu lernen.
Erkennung von Anomalien: ReLU wird in Systemen zur Erkennung von Anomalien eingesetzt, um Ausreißer in großen Datensätzen zu identifizieren. Es wird in Kombination mit Autoencodern verwendet, um das normale Verhalten eines Systems zu lernen und Abweichungen zu erkennen.
Finanzielle Modellierung: ReLU wird in der Finanzmodellierung zur Vorhersage von Aktienkursen, zur Vorhersage finanzieller Risiken und zur Ermittlung von Investitionsmöglichkeiten eingesetzt.
Spracherkennung: ReLU wird in Spracherkennungssystemen eingesetzt, um Sprachsignale zu verarbeiten und in Text umzuwandeln.

Insgesamt ist die ReLU-Funktion eine vielseitige Aktivierungsfunktion, die in verschiedenen Deep-Learning-Anwendungen eingesetzt werden kann, um die Leistung der Modelle zu verbessern.

Das solltest Du mitnehmen

Die Rectified Linear Unit (ReLU) ist eine lineare Aktivierungsfunktion, die immer häufiger beim Training von tiefen Neuronalen Netzwerken eingesetzt wird.
Sie bietet gegenüber anderen, nicht-linearen Aktivierungsfunktionen, wie beispielsweise Sigmoid oder tanh, den Vorteil, dass es kein Problem mit Vanishing Gradients gibt.
Dadurch wird sichergestellt, dass der Fehler von der letzten bis zur ersten Schicht des Netzwerks durchgereicht wird und der Lernprozess dadurch nicht nur schneller, sondern auch robuster gemacht wird.
Bei der herkömmlichen ReLU Funktion kann es jedoch zum Absterben von Neuronen kommen, weshalb die sogenannte Leaky ReLU eingeführt wurde, die für die negativen Werte, Zahlen ungleich Null ausgibt, um diesem Problem entgegenzuwirken.