The dropout layer is a layer used in the construction of neural networks to prevent overfitting. In this process, individual nodes are excluded in various training runs using a probability, as if they were not part of the network architecture at all.

However, before we can get to the details of this layer, we should first understand how a neural network works and why overfitting can occur.

How does a Perceptron work?

The perceptron is originally a mathematical model and was only later used in computer science and Machine Learning due to its ability to learn complex relationships. In its simplest form, it consists of exactly one so-called neuron, which imitates the structure of the human brain.

The perceptron has several inputs at which it receives numerical information, i.e. numerical values. Depending on the application, the number of inputs can differ. The inputs have different weights, which indicate how influential the inputs are for the final output. During the learning process, the weights are changed to produce the best possible results.

The neuron itself then forms the sum of the input values multiplied by the weights of the inputs. This weighted sum is passed on to the so-called activation function. In the simplest form of a neuron, there are exactly two outputs, so only binary outputs can be predicted, for example, “Yes” or “No” or “Active” or “Inactive”, etc.

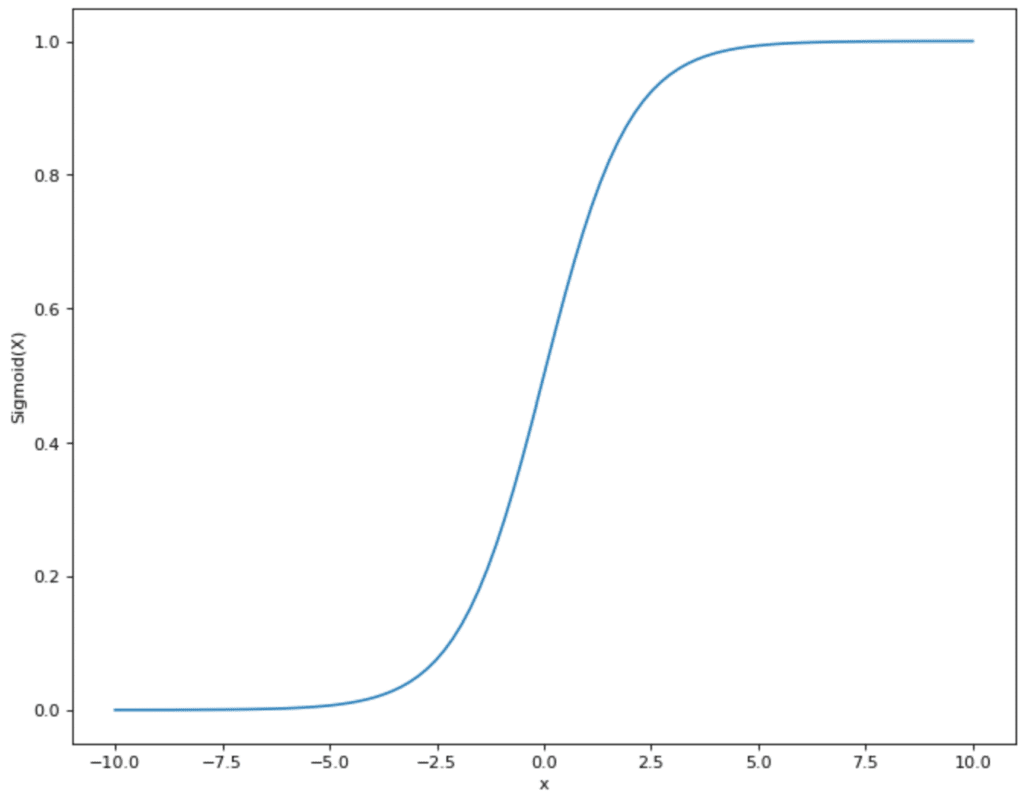
If the neuron has binary output values, a function is used whose values also lie between 0 and 1. An example of a frequently used activation function is the sigmoid function. The values of the function vary between 0 and 1 and actually take these values almost exclusively. Except for x = 0, there is a steep increase and a jump from 0 to 1. Thus, if the weighted sum of the perceptron exceeds x = 0 and the perceptron uses sigmoid as an activation function, the output also changes accordingly from 0 to 1.

What is Overfitting?

The term overfitting is used in the context of predictive models that are too specific to the training data set and thus learn the scatter of the data along with it. This often happens when the model has too complex a structure for the underlying data. The problem then is that the trained model generalizes very poorly, i.e., provides inadequate predictions for new, unseen data. The performance on the training data set, on the other hand, was very good, which is why one could assume a high model quality.

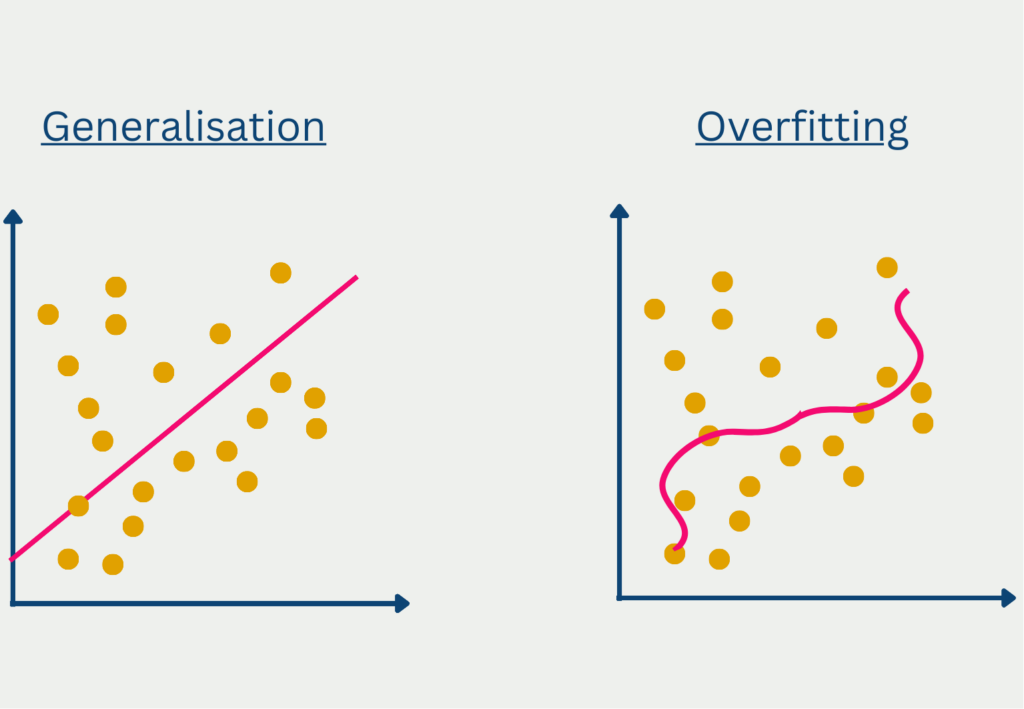
With deep neural networks, it can happen that the complex model learns the statistical noise of the training data set and thus delivers good results in training. In the test data set, however, and especially afterward in the application, this noise is no longer present, and therefore the generalization of the model is very poor.

However, we do not want to abandon the deep and complex architecture of the network, as this is the only way to learn complex relationships and thus solve difficult problems. Before the introduction of the dropout layer, this was a complicated balancing act to find the right architecture that is still complex enough for the underlying problem, but also not prone to overfitting.

How does the Dropout Layer works?

With dropout, certain nodes are set to the value zero in a training run, i.e. removed from the network. Thus, they have no influence on the prediction and also in the backpropagation. Thus, a new, slightly modified network architecture is built in each run and the network learns to produce good predictions without certain inputs.

When installing the dropout layer, a so-called dropout probability must also be specified. This determines how many of the nodes in the layer will be set equal to 0. If we have an input layer with ten input values, a dropout probability of 10% means that one random input will be set equal to zero in each training pass. If instead, it is a hidden layer, the same logic is applied to the hidden nodes. So a dropout probability of 10% means that 10% of the nodes will not be used in each run.

The optimal probability also depends strongly on the layer type. As various papers have found, for the input layer, a dropout probability close to one is optimal. For hidden layers, on the other hand, a probability close to 50% leads to better results.

Why does the dropout layer prevent overfitting?

In deep neural networks, overfitting usually occurs because certain neurons from different layers influence each other. Simply put, this leads, for example, to certain neurons correcting the errors of previous nodes and thus depending on each other or simply passing on the good results of the previous layer without major changes. This results in comparatively poor generalization.

By using the dropout layer, on the other hand, neurons can no longer rely on the nodes from previous or subsequent layers, since they cannot assume that they even exist in that particular training run. This leads to neurons, provably, recognizing more fundamental structures in data that do not depend on the existence of individual neurons. These dependencies actually occur relatively frequently in regular neural networks, as this is an easy way to quickly reduce the loss function and thereby quickly get closer to the goal of the model.

Also, as mentioned earlier, the dropout slightly changes the architecture of the network. Thus, the trained-out model is then a combination of many, slightly different models. We are already familiar with this approach from ensemble learning, such as in Random Forests. It turns out that the ensemble of many, relatively similar models usually gives better results than a single model. This phenomenon is known as the “Wisdom of the Crowds”.

How do you build Dropout into an existing network?

In practice, the dropout layer is often used after a fully-connected layer, since this has comparatively many parameters and the probability of so-called “co-adaptation”, i.e. the dependence of neurons on each other, is very high. However, theoretically, a dropout layer can also be inserted after any layer, but this can then also lead to worse results.

Practically, the dropout layer is simply inserted after the desired layer and then uses the neurons of the previous layer as inputs. Depending on the value of the probability, some of these neurons are then set to zero and passed on to the subsequent layer.

It is particularly useful to use the dropout layers in larger neural networks. This is because an architecture with many layers tends to overfit much more strongly than smaller networks. It is also important to increase the number of nodes accordingly when a dropout layer is added. As a rule of thumb, the number of nodes before the introduction of the dropout is divided by the dropout rate.

What happens to the dropout during inference?

As we have now established, the use of a dropout layer during training is an important factor in avoiding overfitting. However, the question remains whether this system is also used when the model has been trained and is then used for predictions for new data.

In fact, the dropout layers are no longer used for predictions after training. This means that all neurons remain for the final prediction. However, the model now has more neurons available than it did during training. However, as a result, the weights in the output layer are significantly higher than what was learned during training. Therefore, the weights are scaled with the amount of the dropout rate so that the model still makes good predictions.

How to use the dropout layers in Python?

For Python, there are already many predefined implementations with which you can use dropout layers. The best-known is probably that of Keras or TensorFlow. You can import these, like other layer types, via “tf.keras.layers”:

Then you pass the parameters, i.e. on the one hand the size of the input vector and the dropout probability, which you should choose depending on the layer type and the network structure. The layer can then be used by passing actual values in the variable “data”. There is also the parameter “training”, which specifies whether the dropout layer is only used in training and not in the prediction of new values, the so-called inference.

If the parameter is not explicitly set, the dropout layer will only be active for “model.fit()”, i.e. training, and not for “model.predict()”, i.e. predicting new values.

What are the advantages of using a Dropout Layer?

The dropout layer is an additional layer in a neural network that is used for regularization. The integration of this layer offers several advantages, which we will examine in more detail in this section. Originally, it was mostly used to prevent overfitting, but it has now become an important part of deep learning.

• Improved generalization: The most important benefit of the dropout layer is that it improves the generalization performance of the model by preventing overfitting. By. The random deactivation of neurons during training prevents so-called co-adaptation, forcing the model to find and use truly robust features in the data. This feature allows the model to perform better on new, unseen data and has a better overall performance.
• Effective regularization without complex architectures: Furthermore, the dropout layer provides an effective architecture that leads to regularization of the model without increasing the computational power significantly. Traditional regularization methods, such as L1 and L2 regularization, introduce additional parameters that are computationally intensive and potentially difficult to tune. The dropout layer, on the other hand, is easy to implement and changes the network architecture only very slightly. This has made it a popular option for deep learning models.
• Reducing overfitting: The model is overfitted if it specializes too much in the training data during training and learns it by heart. As a result, the model performs poorly on new, unseen data. Dropout reduces the risk of overfitting by throwing out random neurons in each iteration and thus integrating a certain amount of noise into the learning process. This forces the model to learn more robust representations and thus generalize better.
• Simplicity and computational efficiency: The dropout layer is also very easy to integrate when implemented in TensorFlow or PyTorch. This simplicity allows researchers to quickly run different experiments and test whether the performance of the model improves or not. Additionally, it is a popular choice as it does not increase the computational power, making the dropout layer a very efficient regularization technique.
• Robustness against noisy data: Finally, the dropout layer also enables training with noisy data, i.e. data sets that do not have optimal data quality. Without the dropout, there would be a high risk of the model adapting to this noise and thus overfitting because it adapts too strongly to the training data. By omitting the neurons, on the other hand, this risk is reduced as the network cannot adapt too strongly to the existing noise. This is particularly advantageous when the data quality of real information is not always optimal.

In conclusion, the dropout layer is a valuable regularization technique that is particularly important for deep learning applications and offers advantages over established regularization methods. The main positive features are

What are the best practices when working with Dropout Layers?

The dropout layer is an important component of almost any neural network. In this section, we look at best practices for integrating this layer into existing networks and how it can be used to create robust models.

During implementation, the so-called dropout rate must be defined, which determines how many neurons are skipped in each step. A suitable value must be found here. A dropout rate that is too low may not lead to suitable regularization and end up in overfitting. A dropout rate that is too high, on the other hand, can lead to the model not being able to learn effectively and therefore not converging.

The dropout layer must then be placed correctly in the network. There are various ways of integrating these according to fully-connected or convolutional layers. There is no rule of thumb as to which implementation makes the most sense. Instead, it should be experimented with in several training runs to find the optimum position.

However, there is one rule when placing the layer, namely that the dropout layer on the output layer should be avoided, especially for classification tasks. This can lead to undesirable randomness in the predictions and thus negatively affect the performance of the overall model.

In addition, the dropout layer must be used consistently in both the training and testing phases to keep the architecture constant. The difference here, however, is that the dropout rate is set to 0 in the test phase to be able to make accurate predictions.

By constantly monitoring the performance of the model, you ensure that the dropout layer has been used optimally and that the dropout rate has been selected correctly. This also allows you to intervene at an early stage if the model is not converging sufficiently or is slipping into overfitting. In TensorFlow, for example, TensorBoard can be used to continuously monitor the development of the loss function to detect deviations at an early stage.

It should then also be checked whether it makes sense to combine the dropout layer with other regularization techniques such as L1 or L2. This can make sense in some cases and should therefore always be considered.

Building deep learning models is always an iterative process that may require experimentation and fine-tuning. The same naturally also applies to the use of dropout layers. It is necessary to check which dropout rate is optimal or at which point the layer is installed.

This is what you should take with you

• A dropout is a layer in a neural network that sets neurons to zero with a defined probability, i.e. ignores them in a training run.
• In this way, the danger of overfitting can be reduced in deep neural networks, since the neurons do not form a so-called adaptation among themselves, but recognize deeper structures in the data.
• The dropout layer can be used in the input layer as well as in the hidden layers. However, it has been shown that different dropout probabilities should be used depending on the layer type.
• However, once the training has been trained out, the dropout layer is no longer used for predictions. However, in order for the model to continue to produce good results, the weights are scaled using the dropout rate.

Other Articles on the Topic of Dropout Layer

You can find the documentation of the TensorFlow Dropout Layer here.