The Rectified Linear Unit (ReLU) activation function is a special function that is used for training neural networks and has become established in recent years. In short, it is a linear function that maintains positive values and sets negative values to zero.

What is an Activation Function?

The activation function occurs in the neurons of a neural network and is applied to the weighted sum of input values of the neuron. Because the activation function is non-linear, the perceptron can also learn non-linear correlations.

Thus, the neural networks get the property to learn and map complex relationships. Without the non-linear function, only linear dependencies between the weighted input values and the output values could be created. Then, however, one could also use linear regression. The processes within a perceptron are briefly described in the following.

The perceptron has several inputs, the so-called inputs, at which it receives numerical information, i.e. numerical values. Depending on the application, the number of inputs may differ. The inputs have different weights that indicate how influential the inputs are to the eventual output. During the learning process, the weights are changed to produce the best possible results.

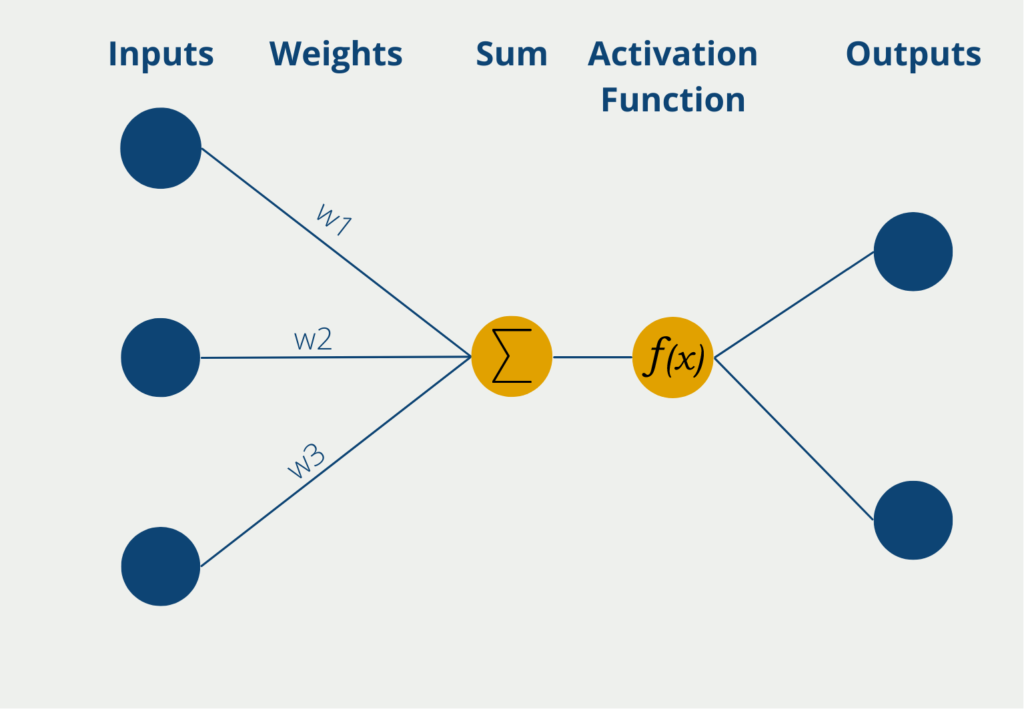
The neuron itself then forms the sum of the input values multiplied by the weights of the inputs. This weighted sum is passed on to the so-called activation function. In the simplest form of a neuron, there are exactly two outputs, so only binary outputs can be predicted, for example, “Yes” or “No” or “Active” or “Inactive”, etc.

If the neuron has binary output values, an activation function is used whose values also lie between 0 and 1. Thus, the output values result directly from the use of the function.

What Activation Functions are there?

Many different activation functions are used in Machine Learning. Among the most common are:

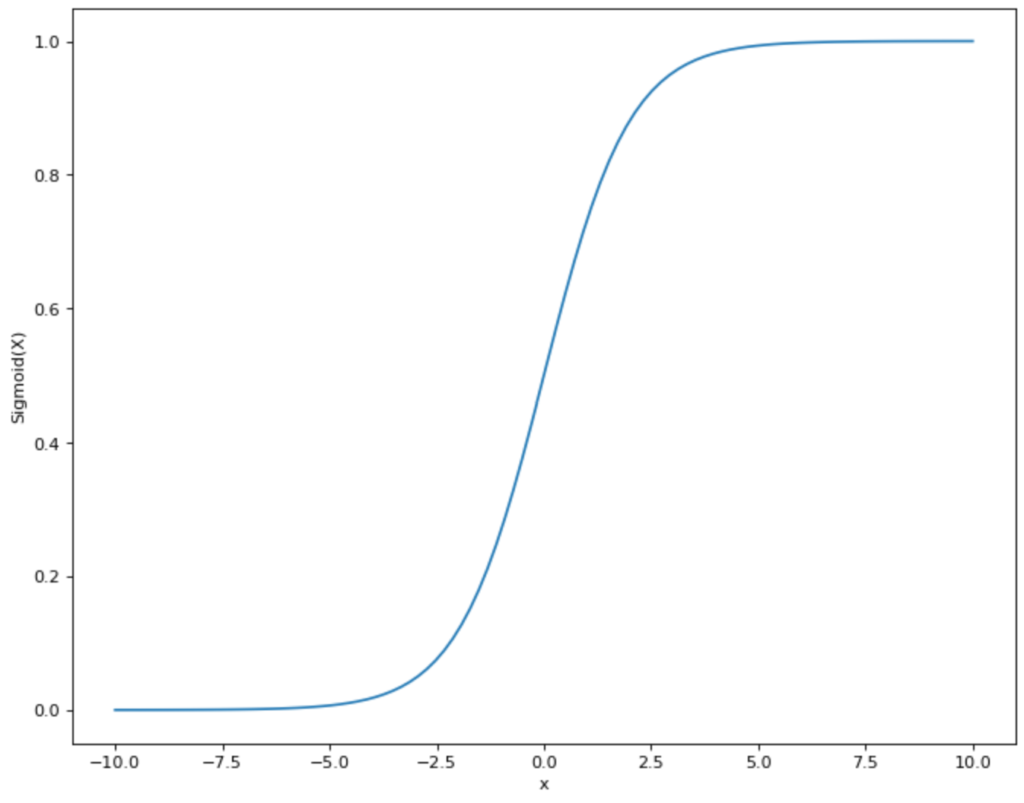
• Sigmoid function: This function maps the input values to the range between 0 and 1.
• Tanh function: The Tanh function, or tangent hyperbolic, map the input values to the range between -1 and 1.
• Softmax function: The softmax function also maps the input values to the range between 0 and 1, but is particularly suitable for the last layer in the neural network, to represent a probability distribution there.

What are the problems with these Activation Functions?

All of the functions mentioned are so-called non-linear activation functions, which means that they are not proportional to the x variable. In concrete terms, this means that an increase in x by one does not necessarily mean an increase in y by one.

These non-linear functions offer the advantage of being able to recognize and learn even complex relationships between the input and output variables. However, these functions have the following problems due to their progression:

• Vanishing Gradient / Saturation: As we can see from the course of the sigmoid function, the function runs almost parallel to the x-axis for very large and very small x-values. The derivative or gradient is almost zero at these points since the function has no real slope at these points. However, in what is called backpropagation, or the learning process of the network, this results in almost no learning effect for large and small x values, since the gradient is zero.
• Non-zero-centered: Both the sigmoid and the softmax function move between the y-values 0 and 1 and are thus not zero-centered, i.e. their mean value is not 0. In the learning process, this can become problematic, since the weights then always have the same sign, namely either all positive or all negative. Under certain circumstances, this can lead to an erratic learning process. However, this problem can be counteracted by performing normalization and thus zero-centering the input data.

What is the Rectified Linear Unit (ReLU) activation function?

The Rectified Linear Unit (ReLU for short) is a linear activation function that was introduced to solve the vanishing gradient problem and has become increasingly popular in applications in recent years. In short, it keeps positive values and sets negative input values equal to zero. Mathematically, this is expressed by the following term:

\(\) \[ f(x) = \begin{cases}
x & \text{if x ≥ 0}\\
0 & \text{if x < 0}
\end{cases} \]

What are the advantages and disadvantages of this function?

The ReLU activation function has gained acceptance primarily because of the following advantages:

• Easy calculation: Compared to the other options, the ReLU function is very easy to calculate and thus saves a lot of computing power, especially for large networks. This translates into either lower cost or lower training time.
• No vanishing gradient problem: Due to the linear structure, the asymptotic points that are parallel to the x-axis do not exist. As a result, the gradient is not vanishing and the error passes through all layers even for large networks. This ensures that the network actually learns structures and significantly accelerates the learning process.
• Better results for new model architectures: Compared to the other activation functions, ReLU can set values equal to zero, namely as soon as they are negative. In contrast, for the sigmoid, softmax, and tanh functions, the values only approach zero asymptotically but never become equal to zero. However, this leads to problems in newer models, such as autoencoders when creating deep fakes, since real zeros are needed in the so-called code layer to achieve good results.

However, there are also problems with this simple activation function. Because negative values are consistently set equal to zero, it can happen that individual neurons also have a weighting equal to zero, since they make no contribution to the learning process and thus “die off”. For individual neurons, this may not be a problem at first, but it has been shown that in some cases even 20 – 50 % of the neurons can “die” due to ReLU.

What is the Leaky ReLU function?

To overcome this drawback and thus make the ReLU function more robust, an optimization of the function has been formed called Leaky ReLU. Compared to the conventional version of the function, negative values are not set equal to zero, but they are given a positive slope (albeit small). Mathematically, this looks like this:

\(\) \[ f(x) = \begin{cases}
x & \text{if x ≥ 0}\\
\alpha x & \text{if x < 0}
\end{cases} \]

The parameter α is a positive constant that must be determined before training and thus does not represent a hyperparameter that is changed during training. It ensures that the negative values cannot take the value zero and thus prevents the “death” of neurons.

What applications use the ReLU activation function?

The rectified linear unit (ReLU) function is a commonly used activation function in Deep Learning. It has several applications in different domains, including:

• Computer Vision: ReLU is commonly used in foldable neural networks (CNNs) for tasks such as image classification, object recognition, and segmentation. These models otherwise have a high risk for whole neurons to fall out of the model.
• Natural language processing: ReLU is used in recurrent neural networks (RNNs) for tasks such as sentiment analysis, machine translation, and text classification.
• Recommender systems: ReLU is used in Deep Learning based recommender systems to learn user-item interaction patterns from large datasets.
• Anomaly detection: ReLU is used in anomaly detection systems to identify outliers in large datasets. It is used in combination with autoencoders to learn the normal behavior of a system and detect deviations.
• Financial Modeling: ReLU is used in financial modeling to predict stock prices, predict financial risks, and identify investment opportunities.
• Speech Recognition: ReLU is used in speech recognition systems to process speech signals and convert them into text.

Overall, the ReLU function is a versatile activation function that can be used in various applications.

This is what you should take with you

• The Rectified Linear Unit (ReLU) is a linear activation function that is increasingly used in deep neural network training.
• It offers the advantage over other non-linear activation functions, such as sigmoid or tanh, that there is no problem with vanishing gradients.
• This ensures that the error is passed from the last to the first layer of the network, making the learning process not only faster but also more robust.
• However, with the conventional ReLU function, neurons can die, which is why the so-called Leaky ReLU was introduced, which outputs non-zero numbers for the negative values to counteract this problem.

Other Articles on the Topic of ReLU

The TensorFlow documentation for the ReLU activation function can be found here.