Integrated Gradients ermöglicht es die Inputs eines Deep Learning Modells auf ihre Wichtigkeit für die Ausgabe hin zu untersuchen. Ein großer Kritikpunkt an tiefen Neuronalen Netzwerken ist die fehlende Interpretierbarkeit, wie wir sie beispielsweise von einer Linearen Regression kennen. Dort können wir anhand der Gewichtungen relativ genau sagen, wie sehr eine unabhängige Variable den Wert der Vorhersage beeinflusst.

Die Hidden Layer des Neuronalen Netzwerkes lassen diese Beziehung zwischen Eingabe und Ausgabe jedoch stark verschwimmen, da es keine direkte Verknüpfung zwischen Input und Output Layer gibt. In einem Modell mit hundert Neuronen ist es bereits nicht mehr praktikabel, den Weg eines Datensatzes durch das Netzwerk zu verfolgen, um so vielleicht die Funktionsweise des Modells interpretieren zu können.

Wie funktioniert der Integrated Gradient?

Integrated Gradients wurden erstmal im Jahr 2017 in dem Paper Axiomatic Attribution for Deep Networks eingeführt und getestet. Darin wird versucht jedem Inputwert einen Attributionswert zuzuordnen. Dieser sagt aus, wie stark die Eingabe zur Vorhersage beigetragen hat. Dieser Ansatz kann für Klassifizierungsmodelle, beispielsweise im Bereich Natural Language Processing (NLP) oder beim Labeln von Bildern, genutzt werden. Wir werden uns in diesem Artikel auf Sentiment Analysen im Bereich des NLP beschränken, da unser folgendes Codebeispiel darauf basiert. Für die Klassifizierung von Bildern funktioniert der Algorithmus in leicht abgewandelter Form. Unser Beispiel übernehmen wir dazu größtenteils von hier.

In einem Beispiel wollen wir anhand eines Satzes oder einer Sequenz entscheiden, ob es sich um eine positive oder negative Bewertung handelt. Die Integrated Gradients Methode startet mit der sogenannten Baseline, also einem Ausgangspunkt, der keine Information enthält für die Modellvorhersage. In unserem Fall ist das der Satz ausschließlich mit dem Anfangs- und Endtoken. Diese markieren nur den Anfang und das Ende eines Satzes oder Abschnittes und geben keine Aussage darüber, ob die Bewertung positiv oder negativ ist.

Wir definieren eine gewisse Anzahl an Schritten, die bestimmt, in wie vielen Stufen wir von der Baseline zum eigentlichen Input des Modells gelangen. Laut dem ursprünglichen Paper sollte die Anzahl an Schritten zwischen 20 und 300 liegen. Bildlich und stark vereinfacht kann man sich das in etwa so vorstellen, als würden wir den Satz Stück für Stück zusammenbauen und in jedem Schritt das nächste Token der Baseline hinzufügen.

In jedem dieser Schritte würden wir uns dann vom Modell eine Vorhersage berechnen lassen. Dadurch bekommen wir für jedes Input Feature einen Attributionswert, der aussagt wie stark das Feature das Gesamtergebnis beeinflusst hat. Wenn wir beispielsweise der Baseline das Token für das Wort “gut” hinzufügen, werden wir wahrscheinlich einen Anstieg der Vorhersage beobachten, da der Outputwert 1 des Models für eine positive Bewertung steht. Den Attributionswert für das Token “gut” können wir explizit berechnen, indem wir den Gradienten des Modells mit Bezug auf das Input Feature “gut” berechnen.

Warum funktioniert die Integrated Gradients Methode?

Wenn wir versuchen solche Einflussfaktoren zu ermitteln, stehen wir vor dem Problem, dass wir im Nachhinein nicht beurteilen können, ob ein falscher Attributionswert auf einem Fehler des Modells oder der Attributionsmethode beruht. Deshalb werden in der Literatur zwei Grundprinzipien genannt, die eine Attributionsmethode erfüllen muss, um zuverlässig gute Ergebnisse zu liefern. Im Paper Axiomatic Attribution for Deep Networks können die Autoren zeigen, dass Integrated Gradients die beiden folgenden Prinzipien erfüllen und somit eine gute Attributionsmethode darstellen:

1. Sensitivität: Wenn ein Input Feature die Klassifizierung in irgendeiner Weise verändert, sollte diese Eingabe einen Attributionswert ungleich 0 haben.
2. Implentierungsinvarianz: Das Ergebnis der Attribution darf nicht vom Aufbau und der Struktur des Neuronalen Netzwerkes abhängen. Wenn also zwei unterschiedliche Neuronale Netze für gleiche Inputs die gleiche Vorhersage liefern, sollen deren Attributionswerte auch identisch sein.

Wofür kann Integrated Gradients genutzt werden?

Wie der Name bereits verrät kann das Konzept lediglich für differenziertere Modelle genutzt werden, also solche, die eine Verlustfunktion mithilfe des Gradientenverfahrens optimieren. Dazu zählen alle Arten von Neuronalen Netzwerken, sowie einige andere Modelle. Lediglich grundlegende Modelle im Bereich des Machine Learnings, wie beispielsweise Random Forest oder die Lineare Regression, können nicht genutzt werden.

Die Integrated Gradient Methode kann somit in den verschiedensten Bereichen, wie beispielsweise im Natural Language Processing, in der Bildverarbeitung oder in anderen Vorhersagemodellen, genutzt werden. Zusätzlich können verschiedene Ziele verfolgt werden:

• Es kann herausgefunden werden, wie wichtig einzelne Inputparameter für das schlussendliche Ergebnis sind. Dadurch lassen sich beispielsweise unwichtige Inputs aus dem Datensatz entfernen und es kann Speicherplatz und Rechenleistung in der Vorverarbeitung gespart werden.
• Wenn man die wichtigen Features herausgefunden hat, kann man zusätzlich sicherstellen, dass deren Qualität im Datensatz ausreichend gut ist und somit die Qualität des gesamten Modells erhöhen. Darunter fällt beispielsweise, dass die wichtigen Features nicht allzu viele leere Zellen besitzen und deren Verteilung auch ausgeglichen ist.
• Die Performance des Modells kann schließlich verbessert werden bzw. ein Debugging stattfinden. Bei falschen Vorhersagen kann dann nämlich herausgefunden werden, wie es zu diesem falschen Zusammenhang kam, bzw. welches Input Feature für den falschen Schluss verantwortlich war.

Was ist die Alibi Bibliothek?

Bevor wir mit dem Beispiel zur Integrated Gradients Methode starten können, sollten wir vorher noch einen genaueren Blick auf die genutzte Python-Bibliothek werfen. Für unseren Code nutzen wir die Alibi-Bibliothek, die eine Integrated Gradients Funktion hat.

Dabei handelt es sich um eine Open-Source Bibliothek, die gezielt für die Interpretation von Machine Learning Modellen erstellt wurde und deshalb auch die gewünschte Funktionalität enthält. Sie kann einfach über pip installiert werden und hat Abhängigkeiten zu allen größeren Machine Learning Bibliotheken, wie beispielsweise TensorFlow oder Scikit-Learn.

Integrated Gradients am Beispiel einer Sentiment Analyse

Da es in diesem Beitrag vor allem um die Erklärung von Integrated Gradients gehen soll, nutzen wir ein vortrainiertes BERT Modell für unsere Sentiment Analyse und trainieren dieses nicht noch zusätzlich. Das sparen wir uns für einen eigenen Beitrag auf.

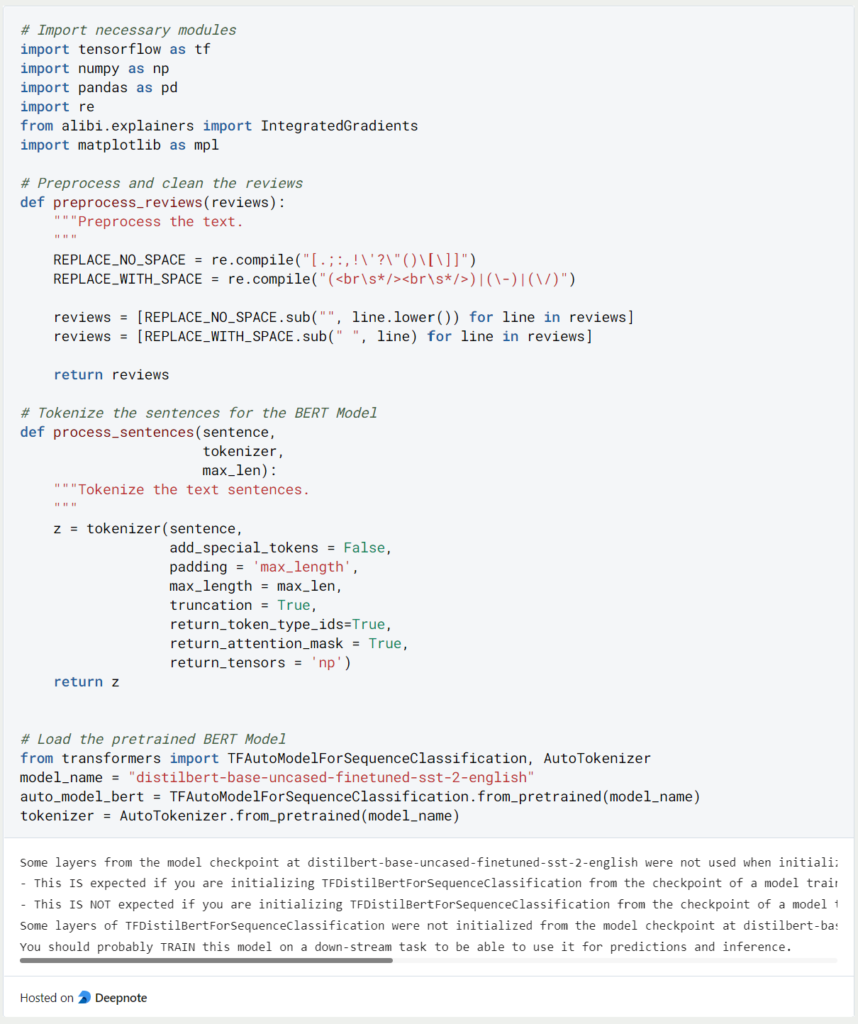
Für unser Beispiel laden wir das Distilbert Modell in englischer Sprache. Das Modell wurde auf dem Datensatz Stanford Sentiment Treebank (SST) für eine Sentiment Analyse trainiert. Wenn wir diese Art von Modellen nutzen, können wir keinen Klartext als Input nutzen, sondern müssen diesen in sogenannte Tokens aufsplitten und diese wiederum als Zahlen repräsentieren. Deshalb benötigen wir die Funktionen “process_reviews” und “process_sentences”.

Damit wir das geladene Modell auch selbst nutzen können, definieren wir einen Wrapper mithilfe dessen wir Sentiment Vorhersagen machen können.

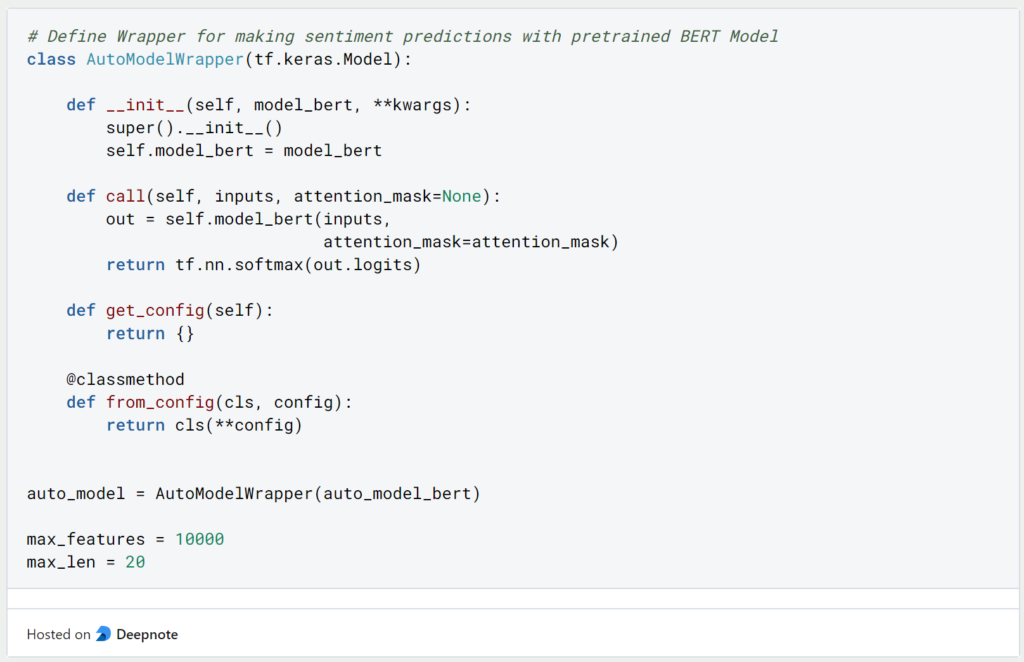
Nun können wir uns endlich den Integrated Gradients und deren Berechnung widmen. Dazu definieren wir den Beispielssatz “I love you, but I also kind of dislike you”, der vielleicht etwas komisch klingen mag, aber nachher gut zeigen wird, welche Worte eher auf ein positives Sentiment und welche auf ein negatives Sentiment hindeuten. Diesen Satz müssen wir natürlich auch erst entsprechend tokenizen, bevor wir eine Vorhersage mit dem Modell machen können.

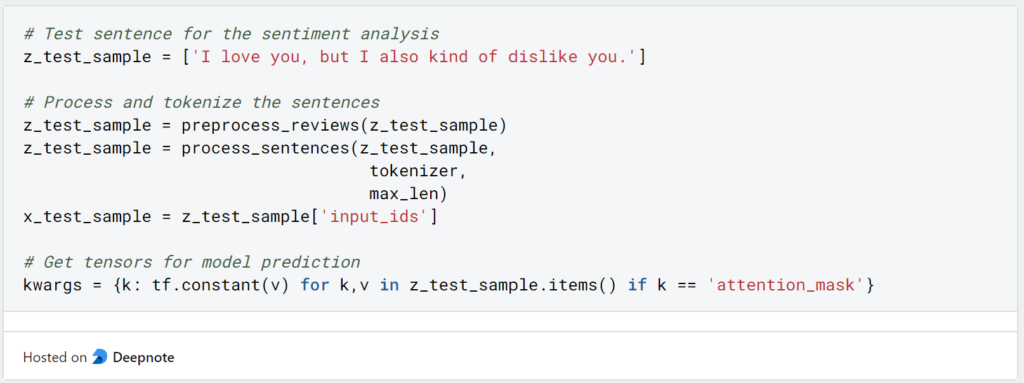
Für die Integrated Gradients benötigen wir nur die Embedding Layer, also den Transformer Block.

Nun können wir den Algorithmus und dessen Hyperparameter definieren. Neben der Anzahl der Schritte, können wir auch die Methode definieren und eine Batch Size vergeben.

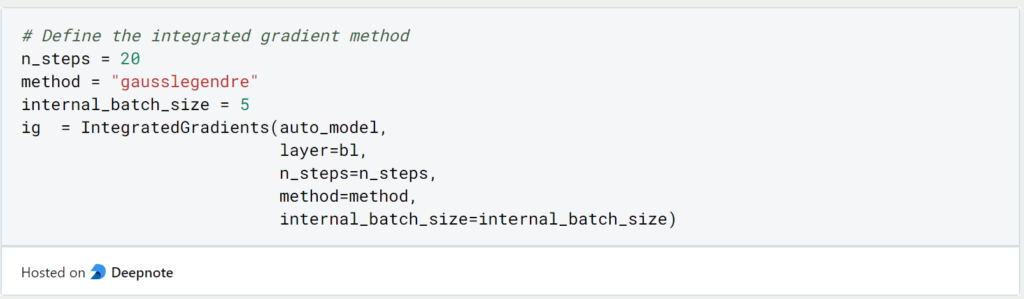
Jetzt kommt der eigentlich spannende Teil dieses Beitrags. Wir lassen erst unser ursprüngliches Klassifizierungsmodell den vollständigen Satz klassifizieren. Auf dieses Ergebnis wenden wir dann die Integrated Gradients Methode an. Wir definieren keine explizite Baseline, sondern nutzen den Default Value.

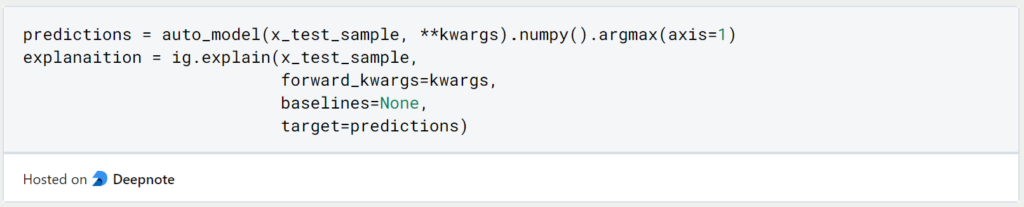
Von diesem Modell können wir die Attributionswerte einfach extrahieren. Die Werte in jedem Schritt addieren wir zusammen, sodass wir anschließend für jede der 20 Stufen einen Wert übrig haben.

Wir definieren nun zwei Funktionen, um uns das Ergebnis der Integrated Gradient Methode auch graphisch aufzeigen zu können und für jedes Wort mit grün und rot farblich erkennen können, wie es zum Sentiment beigetragen hat.

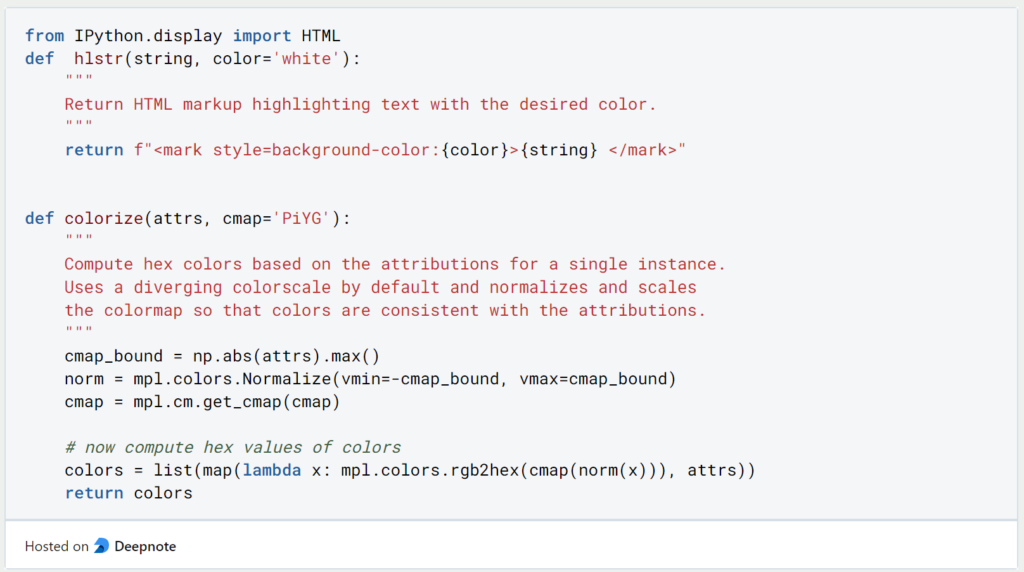
Damit wir ein Ergebnis als Klartext erhalten müssen wir die Tokens wieder zurück in Wörter übersetzen. Die Funktion “colorize” können wir zusätzlich nutzen, um den Attributionswerten die entsprechenden Farbtöne zuzuordnen.

Das Sentiment unseres Satzes klassifiziert das vortrainierte Modell als positiv.

Die grün unterlegten Wörter zeigen uns nun, welche Wörter das Modell zu einer positiven Bewertung geführt haben und die roten Wörter hingegen, welche für eine negative Bewertung gesprochen haben.

Wir sehen, dass das Wort “love” mit Abstand den größten Einfluss auf das positive Sentiment des ganzen Satzes hatte. “Dislike” hingegen hat für eine negative Bewertung des Satzes gesprochen, war aber nicht stark genug, um “love” auszugleichen. Mit einem philosophischeren Satz kann man doch diesen technischen Beitrag nicht beenden.

Das solltest Du mitnehmen

• Die Integrated Gradients Methode ist eine Möglichkeit, um ein Klassifizierungsmodell interpretierbar zu machen.
• Sie kann für alle Modelle genutzt werden, die differenzierbar, also ableitbar, sind. Dazu zählen beispielsweise die Neuronalen Netzwerke, jedoch nicht die grundlegenden Machine Learning Modelle, wie beispielsweise Random Forest oder die Lineare Regression.
• Zu den Anwendungen der Integrated Gradient Methode zählen beispielsweise das Herausfinden der Feature Importance, das Debugging von Modellen, sowie die Aufbesserung des Datensatzes im Bezug auf die wichtigen Features.
• Es wird eine Baseline definiert, die keine Auswirkung auf das Klassifizierungsergebnis hat. Anschließend werden in einigen Schritten Interpolationen an das Modell gegeben und über den Gradient bestimmt, welche Einfluss die einzelnen Inputs auf das Ergebnis haben.

Vielen Dank an Deepnote für das Sponsoring dieses Artikels! Deepnote bietet mir die Möglichkeit, Python-Code einfach und schnell auf dieser Website einzubetten und auch die zugehörigen Notebooks in der Cloud zu hosten.

Andere Beiträge zum Thema Integrated Gradients

• Das Paper “Axiomatic Attribution for Deep Networks” findest Du hier.
• Das Beispiel findest Du in leicht abgewandelter Form hier.