Principal Component Analysis (PCA) is used when you want to reduce the number of variables in a large data set. It tries to keep only those variables in the data set that explain a large part of the variance. All features that correlate strongly with other features are removed.

When do we use Principal Component Analysis?

Various algorithms, such as linear regression, have problems if the data set has variables that are correlated with each other, i.e. depend on each other. To avoid this problem, it can make sense to remove the variables from the data set that correlate with another variable. At the same time, however, the data should not lose its original information content or retain as much information as possible. Principal Component Analysis promises to remove exactly those variables that are correlated with others and do not mean a large loss of information.

Another application of PCA is in cluster analysis, such as k-means clustering, where we need to define the number of clusters in advance. Reducing the dimensionality of the data set helps us to get a first impression of the information and to be able to estimate, for example, which are the most important variables and how many clusters the data set could have. For example, if we manage to reduce the data set to three dimensions, we can visualize the data points in a diagram. From this, the number of clusters can possibly already be read.

In addition, large data sets with many variables also offer the danger that the model overfits. Simply explained, this means that the model adapts too much to the training data during training and thus only delivers poor results for new, unseen data. Therefore, for neural networks, for example, it can make sense to first train the model with the most important variables and then add new variables piece by piece, which may further increase the performance of the model without overfitting. Here, too, Principal Component Analysis is an important tool in the field of Machine Learning.

How does the PCA work?

The core idea of Principal Component Analysis is that possibly several variables in a data set measure the same thing, i.e. are correlated. Thus, the different dimensions can be combined into fewer so-called principal components without compromising the validity of the data set. Body size, for example, has a high correlation with shoe size, since in many cases tall people also have a larger shoe size and vice versa. So if we remove shoe size as a variable from our data set, the information content does not really decrease.

In statistics, the information content of a data set is determined by the variance. This indicates how far the data points are from the center. The smaller the variance, the closer the data points are to their mean value and vice versa. A small variance thus indicates that the mean value is already a good estimate for the data set.

In the first step, PCA tries to find the variable that maximizes the explained variance of the data set. Then, step by step, more variables are added to explain the remaining part of the variance, because the variance, i.e. the deviation from the mean, contains the most information. This should be preserved if we want to train a model based on it.

In the first step, Principal Component Analysis tries to find a line that minimizes the distance between it and the data points as much as possible. This procedure is the same as in linear regression. The line is therefore a summed combination of all individual features of the data set and forms the first principal component.

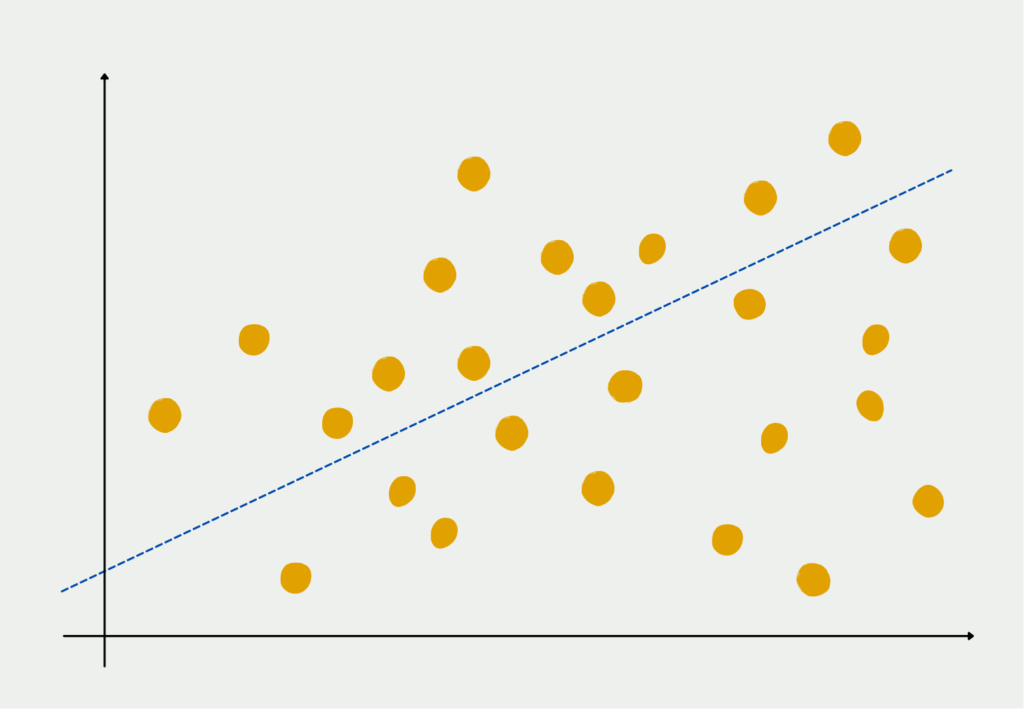
An attempt is then made to create a second line that is orthogonal, i.e. perpendicular, to the first principal component and again minimizes the distance to the data points. The lines must be orthogonal to each other because the principal components should not be correlated with each other and because a perpendicular line is also very likely to explain variance that is not contained in the first component.

How many Principal Components are the target?

There is a correlation between the number of principal components and the remaining information content. This means that with more components you also explain even more variance and thus have information contained in the data set. Very few components, on the other hand, mean that the dimensions have been greatly reduced, which is the purpose of principal component analysis.

According to Kaiser (1960), however, there is a quite good reference point according to which the components can be selected. Only the principal components that have a variance greater than 1 should be selected. Because only these components explain more variance than a single variable in the data set possibly can and really lead to a dimension reduction.

How can the Principal Components be interpreted?

The principal components themselves are very difficult to interpret because they arise as a linear combination of the dimensions. Thus, they represent a weighted mixture of several variables. However, in practical applications, these combinations of variables can also be interpreted concretely.

For example, consider a data set with various information about individuals, such as age, weight, height, creditworthiness, income, savings, and debt. In this dataset, for example, two principal components might emerge. The first principal component would presumably be composed of the dimensions of creditworthiness, income, savings, and debt, and would have high coefficients for these variables. This principal component could then be interpreted, for example, as the person’s financial stability.

What requirements do we need for the Principal Component Analysis?

Compared to similar statistical analyses, Principal Component Analysis has only a few requirements that must be met to obtain meaningful results. The basic properties that the data set should have are:

• The correlation between the features should be linear.
• The data set should be free of outliers, i.e. individual data points that deviate strongly from the mass.
• If possible, the variables should be continuous.
• The result of the PCA becomes better, the larger the sample is.

Not all data sets can be used for Principal Component Analysis without further ado. It must be ensured that the data are approximately normally distributed and interval-scaled, i.e. an interval between two numerical values always has the same spacing. Dates, for example, are interval scaled, because from 01.01.1980 to 01.01.1981 the time interval is the same as from 01.01.2020 to 01.01.2021 (leap years excluded). Above all, interval scaling must be judged by the user and cannot be detected by standardized, statistical tests.

Principal Component Analysis in Python

There are many programs with which principal component analyses can be calculated automatically and the results can be compared with different numbers of components. In Python, this works with the help of the module “Scikit-Learn” whose example we will also take a closer look at here.

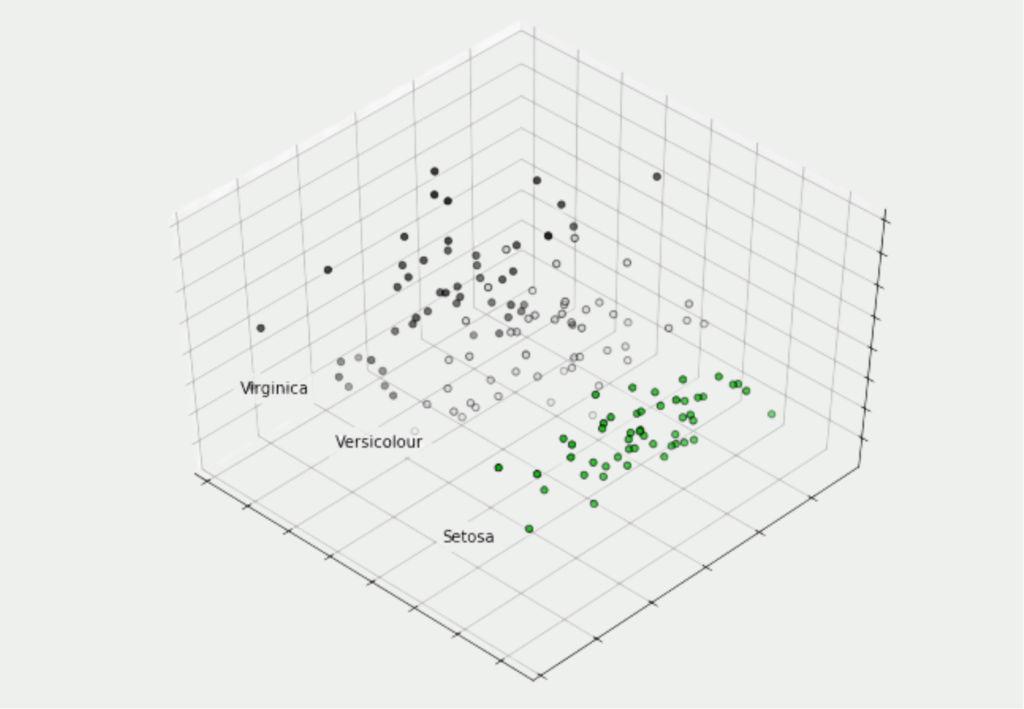
In this application, the so-called Iris Dataset is used. It is a popular training dataset in the field of Machine Learning. It is data from biology, more precise information from so-called iris plants. For each flower, the length and width of the petal and the so-called sepal are available. We store the information about the plants in variable X and the name of the respective flower in variable y.

In our case, we want to try to reduce these four dimensions to three main components in order to be able to visualize them in a three-dimensional diagram. The actual transformation of the data takes place in three lines of code. First, we need to set up a PCA object with the desired number of components. We can then adapt this to our data set and finally have our four-dimensional values converted to three-dimensional values:

With the help of Matplotlib, our results can be visualized in a three-dimensional diagram and it can be seen that even in three dimensions the plants of the same flower species are still close to each other. Thus, no real information content of the data set has been lost.

tSNE vs. Principal Component Analysis

Although the goal of PCA and tSNE is initially the same, namely dimension reduction, there are some differences in the algorithms. First, tSNE works very well for one data set, but cannot be applied to new data points, since this changes the distances between the data points and a new result must be calculated. PCA, on the other hand, produces a rule as a result that can also be applied to new data points that were not yet part of the data set during training.

The t-distributed stochastic neighbor embedding algorithm can also be used when the relationships between data points are non-linear. Principal Component Analysis, on the other hand, can only detect linear dependencies and include them in the separation. For non-linear dependencies, neural networks can also be used, but their effort and training are time-consuming. Although tSNE also has a relatively long training phase compared to PCA, it is usually still shorter than for neural networks and thus represents a good compromise.

Another important difference between PCA and tSNE is the focus on data distribution. Principal Component Analysis tries to maintain the global arrangement of data points even in fewer dimensions. tSNE, on the other hand, focuses more on local distances and correlations, which should be maintained even in lower dimensions. Therefore, it may appear that after a dimension reduction by tSNE, the data looks as if it has already been divided into clusters as well.

This is what you should take with you

• Principal Component Analysis is used for dimension reduction in large data sets.
• It helps in the preprocessing of data for Machine Learning models based on it, such as cluster analyses or linear regressions.
• Certain prerequisites must be met in the data set for PCA to be possible at all. For example, the correlation between the features should be linear.

Thanks to Deepnote for sponsoring this article! Deepnote offers me the possibility to embed Python code easily and quickly on this website and also to host the related notebooks in the cloud.

Other Articles on the Topic of Principal Component Analysis

• You can find a detailed explanation of principal component analysis, including an illustrative video, at our colleagues at Studyflix.
• Schimmelpfennig, H: Known, current and new requirements for driver analyses. In: Keller, B. et al. (Eds.): Marktforschung der Zukunft – Mensch oder Maschine?, Wiesbaden, 2016, pp. 231-243.
• Kaiser, H. F.: The Application of Electronic Computers to Factor Analysis. In: Educational and Psychological Measurement, No. 1/1960, pp. 141-151.