Die Datenanalyse wird vor allem dazu verwendet, Zusammenhänge und Muster zwischen Variablen zu erkennen und zu quantifizieren, damit sie für zukünftige Vorhersagen genutzt und entsprechende Modelle trainiert werden können. Die Korrelationsmatrix ist eine entscheidende Methode, die hilft, die Korrelation, also die Abhängigkeit, zwischen zwei Variablen in einem Datensatz grafisch darzustellen. 

In diesem Artikel beschäftigen wir uns ausgiebig mit dem Konzept der Korrelation und wie die Korrelationsmatrix hilft, die Abhängigkeiten zwischen Variablen aufzuzeigen. Dazu zählt beispielsweise auch, dass wir uns die Berechnung und Interpretation der Korrelationsmatrix im Detail anschauen und erklären, wie eine solche Matrix in Python erstellt werden kann. Zu einem umfassenden Bild gehört auch die Grenzen dieser Methode aufzuzeigen, damit der Einsatz und die Aussagekraft richtig beurteilt werden können. 

Was ist eine Korrelationsmatrix?

Die Korrelationsmatrix ist eine statistische Methode, um die Zusammenhänge zwischen unterschiedlichen Variablen in einem Datensatz zu quantifizieren und gegenüberzustellen. Dabei werden in einer tabellarischen Struktur die paarweisen Korrelationen zwischen allen Kombinationen aus zwei Variablen aufgezeigt. Jede Zelle in der Matrix enthält den sogenannten Korrelationskoeffizienten zwischen den beiden Variablen, die in der Spalte und der Zeile definiert sind.  

Dieser Wert kann zwischen -1 und 1 liegen und gibt Aufschluss darüber, wie sich die beiden Variablen zueinander verhalten. Bei einem positiven Wert liegt eine positive Korrelation vor, sodass ein Anstieg der einen Variablen zu einem Anstieg der anderen Variable führt. Der genaue Wert des Korrelationskoeffizienten gibt Aufschluss darüber, wie stark die Variablen sich zueinander bewegen. Bei einem negativen Korrelationskoeffizienten bewegen sich die Variablen gegenläufig, sodass der Anstieg einer Variablen zu einer Abnahme der anderen Variable führt. Ein Koeffizient von 0 schließlich sagt aus, dass keine Korrelation vorliegt. 

Eine Korrelationsmatrix erfüllt somit den Zweck, die Korrelationen in einem Datensatz auf eine schnelle und einfach verständliche Art und Weise darzustellen und somit die Basis für nachfolgende Schritte zu bilden, wie zum Beispiel die Modellauswahl. Dadurch lässt sich zum Beispiel eine Multikollinearität erkennen, die bei Regressionsmodellen Probleme hervorrufen kann, da die zu erlernenden Parameter verzerrt sind. 

Was ist eine Korrelation?

Die Korrelation bezeichnet das Verhältnis zwischen zwei statistischen Variablen und bewertet, die Stärke und die Richtung der linearen oder nichtlinearen Beziehung der beiden Variablen. Damit wird also quantifiziert, wie sich die Änderung einer Variablen auf die andere auswirkt.

Eine positive Korrelation zweier Variablen bedeutet, dass eine Steigerung von A auch zu einer Steigerung von B führt. Die Abhängigkeit ist dabei ungerichtet. Es gilt also auch im umgekehrten Fall und eine Steigerung der Variable B hat auch einen Anstieg von A zur Folge.

Im Allgemeinen unterscheidet man zwei Arten nach denen die Korrelation beurteilt werden kann: 

• Linear oder Nichtlinear: Die Abhängigkeiten sind linear, wenn die Änderungen in der Variablen A immer eine Änderung mit einem konstanten Faktor bei der Variablen B auslöst. Wenn dies nicht der Fall ist, spricht man von einer nichtlinearen Abhängigkeit. Eine lineare Korrelation besteht beispielsweise zwischen der Körpergröße und dem Körpergewicht. Mit jedem neu gewonnen Zentimeter an Körpergröße nimmt man sehr wahrscheinlich auch eine feste Menge an Körpergewicht zu, solange sich die Statur nicht ändert. Ein nichtlinearer Zusammenhang besteht hingegen zwischen der Umsatzentwicklung und der Aktienkursentwicklung eines Unternehmens. Mit der Zunahme des Umsatzes um 30 % wird sich der Aktienkurs womöglich noch um 10 % erhöhen, hingegen bei den darauffolgenden 30 % Umsatzsteigerung wird der Aktienkurs möglicherweise nur noch um 5 % steigen. 
• Positiv oder negativ: Wenn die Steigerung der Variablen A zu einer Steigerung der Variablen B führt, dann ist eine positive Korrelation gegeben. Wenn hingegen die Steigerung von A zu einer Abnahme von B führt, dann ist die Abhängigkeit negativ. Wenn schließlich eine Änderung von A zu keiner Änderung von B führt, dann liegt keine Korrelation vor und der Korrelationskoeffizient ist entsprechend 0.

Um konkrete Werte für die Korrelation berechnen zu können, wird der sogenannte Korrelationskoeffizient verwendet. Es gibt verschiedene Koeffizienten, die abhängig vom Datensatz und der Art des Zusammenhangs gewählt werden sollten. 

Welche Korrelationskoeffizienten gibt es?

Die Korrelation bezeichnet ein grundlegendes Konzept in der Statistik, welches die Beziehung zwischen zwei Variablen misst und quantifiziert. Es zeigt dabei nicht nur die Richtung des Zusammenhangs an, sondern ermittelt auch den Faktor an, wie stark die Änderung in der einen Variable zu einer Änderung der anderen Variablen führt. Abhängig vom Zusammenhang, der zwischen den Variablen besteht, gibt es verschiedene Möglichkeiten den konkreten Korrelationskoeffizienten zu berechnen. In diesem Abschnitt werden wir uns die drei weit verbreiteten Methoden zur Berechnung der Korrelation genauer anschauen. 

Pearson-Korrelation

Die Pearson-Korrelation wird am häufigsten verwendet, um die Stärke der linearen Beziehung zwischen zwei Variablen zu quantifizieren. Sie kann jedoch nur verwendet werden, wenn angenommen wird, dass die beiden Kenngrößen linear voneinander abhängen und außerdem metrisch skaliert sind, also numerische Werte besitzen. 

Wenn diese Annahmen gegeben sind, kann die Pearson-Korrelation mithilfe von dieser Formel berechnet werden: 

\(\) \[r_{xy} = \frac{\sum (X_i – \overline{X})(Y_i – \overline{Y})}{\sqrt{\sum (X_i – \overline{X})^2} \sqrt{\sum (Y_i – \overline{Y})^2}} \]

Hierbei sind \(X_i\) und \(Y_i\) die Werte der beiden Variablen und \(\overline{X}\) und \(\overline{Y}\) die Mittelwerte der Variablen. Zusätzlich kann diese Formel auch umgeschrieben werden, sodass sie im Nenner die Standardabweichung nutzt: 

\(\) \[r = \frac{ \sum_{i \in D}(x_{i} – \text{mean}(x)) \cdot (y_{i} – \text{mean}(y))}{(n-1) \cdot SD(x) \cdot SD(y)}\]

Die resultierenden Werte liegen dann zwischen -1 und 1, wobei positive Werte auf eine positive Korrelation hindeuten und negative Werte entsprechend auf eine negative Korrelation.

Spearman-Korrelation

Die Spearman-Korrelation erweitert die Annahmen der Pearson-Korrelation und untersucht allgemein die monotone Beziehung zwischen zwei Variablen, ohne jedoch eine lineare Beziehung zu unterstellen. Viel allgemeiner untersucht sie, ob eine Änderung in einer Variablen zu einer Änderung der anderen Variablen führt, auch wenn dieser Zusammenhang nicht linear sein muss. Dadurch eignet sie sich nicht nur für Datensätze mit nichtlinearen Abhängigkeiten, sondern auch für sogenannte ordinale Daten, also Datensätze in denen lediglich die Reihenfolge der Datenpunkte eine wichtige Rolle spielt, nicht aber der genaue Abstand. 

Die Formel für die Spearman-Korrelation basiert auch maßgeblich auf dieser Rangfolge. Dazu werden die Datensätze zuerst nach der ersten Variablen und anschließend nach der zweiten Variable sortiert. Für beide Rangfolgen werden die Ränge beginnend mit 1 für den geringsten Wert durchnummeriert. Anschließend wird für jeden Datenpunkt die Differenz zwischen dem Rang für die erste Variable und dem Rang für die zweite Variable berechnet:

\(\) \[d_i​=\text{Rang}(X_i​)−\text{Rang}(Y_i​)\]

Der Spearman-Korrelationskoeffizient errechnet sich dann mithilfe der folgenden Formel, wobei \(d\) die erklärte Summe für jeden Datenpunkt ist und \(n\) die Anzahl der Datenpunkte im Datensatz. 

\(\) \[\rho = 1 – \frac{6 \sum d_i^2}{n(n^2 – 1)} \]

Kendall-Tau-Korrelation

Die Kendall-Tau-Korrelation ist eine weitere Methode, um einen Korrelationskoeffizienten zu bestimmen. Analog zur Spearman-Korrelation kann sie nicht-lineare Beziehungen zwischen den Daten quantifizieren und arbeitet auf den ordinalen Beziehungen zwischen den Daten. Im Vergleich zur Spearman-Korrelation eignet sie sich besonders bei kleineren Datensätzen und erfasst die Stärke der Beziehung etwas genauer. 

Die Kendall-Tau-Korrelation betrachtet immer Paare von Datenpunkten und unterscheidet dabei konkordante und diskordante Paare. Ein konkordantes Paar an Datenpunkten ist gegeben, wenn ein Paar von Beobachtungen \((x_i, y_i,)\) und \((x_j, y_j)\) in der Rangfolge beider Variablen übereinstimmt. Es muss also gelten, dass wenn \(x_i > y_i\), dann gilt auch \(x_j > y_j\). Stimmt die Rangfolge hingegen nicht überein, dann gilt das Paar als diskordant. 

Die Formel zur Berechnung der Kendall-Tau-Korrelation ergibt sich dann mithilfe der folgenden Formel: 

\(\) \[ \tau = \frac{(\text{Anzahl der konkordanten Paare}) – (\text{Anzahl der diskordanten Paare})}{\frac{1}{2}n(n-1)} \]

Korrelation vs. Kausalität

Die Korrelation bezeichnet das Verhältnis zwischen zwei statistischen Variablen und bewertet, die Stärke und die Richtung der linearen oder nichtlinearen Beziehung der beiden Variablen. Damit wird also quantifiziert, wie sich die Änderung einer Variablen auf die andere auswirkt.

Eine Kausalität hingegen beschreibt einen Ursache-Wirkungs-Zusammenhang zwischen zwei Variablen. Eine Kausalität zwischen A und B bedeutet also, dass die Steigerung in A auch die Ursache für die Erhöhung von B ist. 

Der Unterschied wird an einem einfachen Beispiel schnell deutlich. Eine Studie könnte sehr wahrscheinlich einen positiven Zusammenhang zwischen dem Hautkrebsrisiko eines Menschen und der Anzahl an Freibadbesuchen finden. Wenn eine Person also häufig das Freibad besucht, dann erhöht sich auch ihr Risiko an Hautkrebs zu erkranken. Eine eindeutige positive Abhängigkeit. Doch besteht auch eine Kausalität zwischen Freibadbesuchen und Hautkrebs? Wahrscheinlich eher nicht, denn das würde bedeuten, dass alleinig die Freibadbesuche die Ursache für das erhöhte Hautkrebsrisiko sind.

Vielmehr ist es so, dass Menschen, die sich häufiger im Freibad aufhalten auch deutlich mehr Sonneneinstrahlung ausgesetzt sind. Wenn dann nicht ausreichend mit Sonnencreme oder ähnlichem vorgesorgt wird, kann es zu mehr Sonnenbränden kommen und diese erhöhen das Hautkrebsrisiko. Man sieht deutlich, dass die Korrelation zwischen Freibadbesuchen und Hautkrebsrisiko keine Kausalität sind. 

Eine Vielzahl von kuriosen Zusammenhängen, die sehr wahrscheinlich keine Kausalität aufzeigen, finden sich auf tylervigen.com. 

Wie berechnet man eine Korrelationsmatrix?

Die Korrelationsmatrix ist eine tabellarische Struktur, in der die paarweise Korrelationen zwischen unterschiedlichen Variablen in einem Datensatz abgebildet werden. Jede Zelle in dieser Matrix beschreibt, wie stark diese zwei Variablen aus dem Zeilen- und Spaltenindex miteinander in Verbindung stehen. Dieser Zusammenhang wird mithilfe des Korrelationskoeffizienten \(r_{ij}\) quantifiziert, welcher den Zusammenhang der Variablen \(X_i\) mit \(X_j\) misst. 

Der allgemeine Aufbau der Matrix ergibt sich dann wie folgt: 

\(\) \[ K = \begin{pmatrix} r_{11} & r_{12} & \dots & r_{1n} \\ r_{21} & r_{22} & \dots & r_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ r_{n1} & r_{n2} & \dots & r_{nn} \\ \end{pmatrix} \]

Hierbei sind: 

• \(K\) ist die gesuchte Korrelationsmatrix. 
• \(r_{ij}\) ist der Korrelationskoeffizient für die Variablen \(X_i\) und \(X_j\). 
• \(n\) ist die Anzahl der Variablen im Datensaatz. 

Für den Korrelationskoeffizienten können zum Beispiel die verschiedenen Methoden genutzt werden, welche im vorherigen Abschnitt vorgestellt werden. Damit diese Matrix nicht von Hand befüllt werden muss, gibt es verschiedene Programme, die für die Erstellung genutzt werden können: 

• In Excel gibt es im Bereich der Datenanalyse eine integrierte Korrelationsfunktion. 
• Python bietet verschiedene Möglichkeiten zur Berechnung. In Pandas kann man beispielsweise aus einem DataFrame direkt die Korrelationsmatrix erstellen. Eine ähnliche Möglichkeit gibt es darüber hinaus auch in NumPy. 
• In der Programmiersprache R kann das ganze über die Funktion cor() erreicht werden. 
• Auch Matlab bietet die Funktionalität, um eine Korrelationsmatrix erstellen zu können. 

Vor der Erstellung der Matrix ist es außerdem wichtig, dass der Datensatz ausreichend von fehlenden Werten und Ausreißern bereinigt wurde, da diese sonst einen negativen Einfluss auf die Korrelationsergebnisse haben können. 

Wie interpretiert man eine Korrelationsmatrix?

Die Korrelationsmatrix ist eine kompakte Darstellung, um die Abhängigkeiten zwischen unterschiedlichen Variablen in einem Datensatz zu veranschaulichen. Jede Zahl in der Matrix gibt dabei den Korrelationskoeffizienten zwischen zwei Variablen an. Es dabei verschiedene Kennwerte, die Aussagen über die zugrundeliegenden Korrelationen liefern.

Richtung der Korrelation

Die Richtung der Korrelation gibt an, wie sich die Variablen miteinander verhalten. Eine positive Korrelation, also zum Beispiel \(r_{ij} = 0.8\), bedeutet, dass die beiden Variablen positiv korreliert sind. Dies sagt aus, dass der Anstieg von einer Variablen auch zu einem Anstieg der anderen Variablen führt und umgekehrt. Es könnte beispielsweise eine positive Korrelation zwischen der Anzahl von Verkaufsmitarbeiter und dem Umsatz eines Unternehmens bestehen, sodass eine steigende Anzahl an Verkaufsmitarbeitern auch zu einem steigenden Umsatz führt. 

Eine negative Korrelation, also zum Beispiel \(r_{ij} = -0.7\), liegt vor, wenn der Anstieg in der einen Variablen zu einem Absinken der anderen Variable führt. Eine negative Korrelation besteht beispielsweise zwischen der Arbeitslosigkeit und dem Wirtschaftswachstum. Wenn die Arbeitslosigkeit steigt, dann sinkt meist das Wirtschaftswachstum und umgekehrt. 

Stärke der Korrelation

Neben dem Vorzeichen des Korrelationskoeffizienten, gibt auch der absolute Wert wichtige Informationen über den Zusammenhang. Werte nahe den Endpunkten -1 und 1 stehen für eine starke Korrelation zwischen den Variablen, während Werte nahe der 0 für keine oder nur eine sehr schwache Korrelation stehen. 

Symmetrie der Matrix

Eine wichtige Eigenschaft der Korrelationsmatrix ist ihre Symmetrie. Das bedeutet, dass alle Elemente oberhalb der sogenannten Hauptdiagonalen identisch sind mit den Werten unterhalb der Hauptdiagonalen. Dadurch wird die Interpretation der Matrix vereinfacht, da lediglich die Hälfte der Werte untersucht werden muss. 

Die Symmetrie der Korrelationsmatrix ergibt sich einfach gesagt aus der Eigenschaft, dass der Korrelationskoeffizient zwischen \(X_i\) und \(X_j\) identisch ist zum Korrelationskoeffizienten zwischen \(X_j\) und \(X_i\), also \(r_{ij} = r_{ji}\).

Muster

Beim Betrachten der Matrix sollte außerdem darauf geachtet werden, ob Muster zu erkennen sind, die helfen den Datensatz weiter zu vereinfachen. Zum Beispiel sollte man untersuchen, ob es mehrere Variablen gibt, die zu einer Variablen eine hohe Korrelation aufweisen. Diese können möglicherweise zu einem Cluster zusammengefasst werden, da sie ähnliche Merkmale messen. Zum Beispiel könnten die Variablen „Körperliche Betätigung in Stunden pro Woche“ und „Maximale Anzahl an Liegestützen“ beide eine hohe Korrelation mit einem niedrigen Körpergewicht haben, da beide Variablen als körperliche Fitness zusammengefasst werden können. 

Multikollinearität

Bei der Interpretation der Korrelationsmatrix ist es wichtig, die Werte mit hohen Korrelationen genauer zu untersuchen. Diese können auf eine sogenannte Multikollinearität hinweisen, was bedeutet, dass zwei oder mehrere Variablen stark miteinander korrelieren. Diese Eigenschaft ist in verschiedenen statistischen Modellen, wie beispielsweise Regressionen, problematisch und sollte vor dem Modelltraining beseitigt werden. Wenn dies nicht geschieht, kann es zu verzerrten Ergebnissen bei der Parameterschätzung kommen. 

Welche Möglichkeiten gibt es die Korrelationsmatrix zu visualisieren?

Die Visualisierung einer Korrelationsmatrix soll dabei helfen, schnell und einfach einen Überblick über die Korrelationen zwischen Variablen zu bekommen. Dies ist vor allem bei großen Datensätzen von Bedeutung, um einen groben Überblick zu erhalten. In diesem Abschnitt stellen wir verschiedene Methoden vor, die dafür genutzt werden können. 

Heatmaps

Eine Heatmap wird am häufigsten verwendet, um die Werte einer Korrelationsmatrix zu visualisieren. Dabei werden alle Variablen im Datensatz als Zeile und Spalte abgetragen. Die Hintergrundfarbe der einzelne Felder bestimmt sich dann über die Korrelation zwischen der Variablen der Zeile und der Variablen der Spalte. Normalerweise ist es so, dass die Werte dunkler sind, umso stärker die Korrelation ist und heller, umso schwächer die Korrelation zwischen den Variablen. 

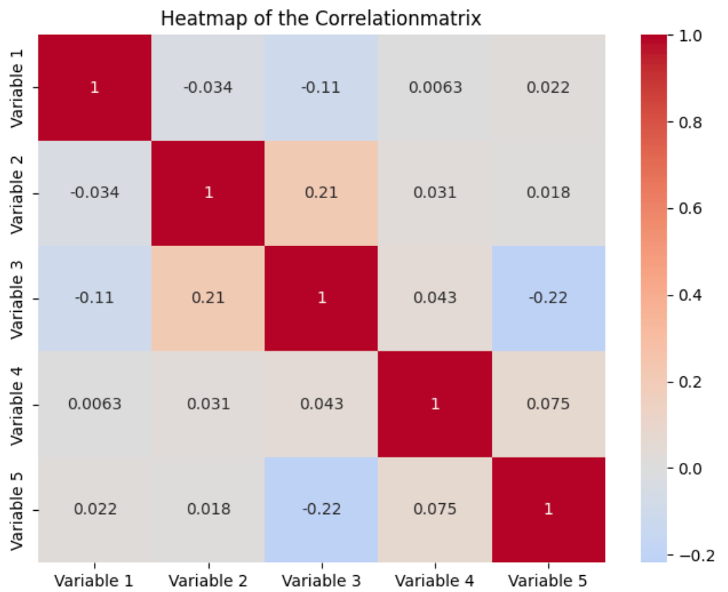
Zusätzlich zu den Farben werden auch die tatsächlichen Werte abgebildet. Auf der Hauptdiagonalen der Matrix sind alle Werte eins, da dies die Felder sind, bei denen Zeilen- und Spaltenvariable identisch sind. Durch die Kombination aus Werten und Farben bieten Heatmaps eine einfache Möglichkeit die Korrelationen schnell verständlich zu machen, wodurch sich Muster und Anomalien leichter identifizieren lassen. 

Clusteranalyse

Die Clusteranalyse kann verwendet werden, um stark korrelierte Variablen zu gruppieren. Dabei lassen sich Variablen mit ähnlichen Korrelationen in Cluster zusammenfassen und visualisieren. Dies vereinfacht es, Variablen mit ähnlichem Verhalten zu identifizieren und Zusammenhänge zu erkennen. 

Vor allem bei größeren und komplexen Datensätzen bietet die Clusteranalyse eine zusätzliche Visualisierungsmöglichkeit, falls einfache Heatmaps nicht ausreichend sind. 

Scatterplot

Neben der Korrelationsmatrix können auch Scatterplots verwendet werden, um die Abhängigkeiten zwischen zwei Variablen zu visualisieren. Dadurch erkennt man, wie sich die beiden Werte zueinander bewegen und es kann herausgefunden werden, ob die Beziehung linear oder nichtlinear ist. Durch die Kombination von verschiedenen Scatterplots können diese Abhängigkeiten auch für einen kompletten Datensatz visualisiert werden. 

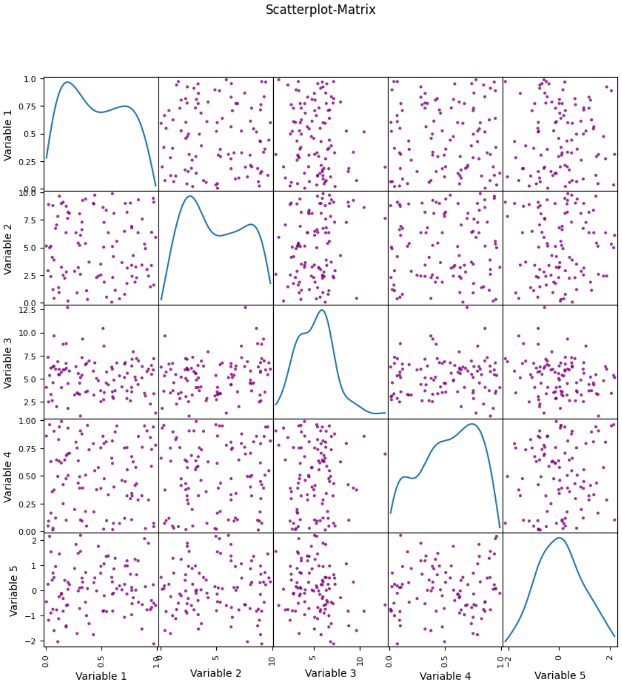
Wie kann eine Korrelationsmatrix in Python visualisiert werden?

In Python kann eine Korrelationsmatrix einfach mithilfe von Pandas errechnet und anschließend mit Seaborn als Heatmap visualisiert werden. Zur Veranschaulichung generieren wir zufällig Daten mithilfe von NumPy und legen diese in einem DataFrame ab. Sobald die Daten in einem DataFrame abliegen, kann mithilfe der Funktion corr() die Korrelationsmatrix erstellt werden. 

Wenn innerhalb der Funktion keine Parameter definiert werden, wird standardmäßig der Pearson-Koeffizient zur Berechnung der Korrelationsmatrix genutzt. Anonsten kann man auch über den Paramter method einen anderen Korrelationskoeffizienten definieren. 

Abschließend wird dann die Heatmap mithilfe von seaborn visualisiert. Dazu wird die heatmap() Funktion aufgerufen und die Korrelationsmatrix übergeben. Unter anderem kann über die Parameter bestimmt werden, ob die Beschriftungen hinzugefügt werden sollen und es kann die Farbpalette bestimmt werden. Mithilfe von matplolib wird dann schließlich das Diagramm dargestellt. 

Was sind die Grenzen der Korrelationsmatrix?

Die Korrelationsmatrix ist ein sehr nützliches Werkzeug, um Beziehungen und Korrelationen zwischen Variablen in einem Datensatz zu erkennen und zu veranschaulichen. Jedoch hat diese Methode auch ihre Grenzen und die folgenden Punkte sollten bei der Interpretation der Ergebnisse beachtet werden: 

• Kausalität vs. Korrelation: Wie wir in einem vorherigen Abschnitt schon beleuchtet haben, ist eine Korrelation lediglich ein Indikator für eine mögliche Kausalität. Eine hohe Korrelation bedeutet lediglich, dass zwei Variablen miteinander in Verbindung stehen. Für den Nachweis einer Kausalität hingegen müssen aufwendige Experimente gemacht und deren Ergebnisse untersucht werden.  
• Outlier & nichtlineare Beziehungen: Damit die Ergebnisse der Korrelationsmatrix aussagekräftig sind, muss die Wahl des Korrelationskoeffizienten intensiv überdacht werden. Der standardmäßige Pearson-Koeffizient ist anfällig für Ausreißer und lässt sich dadurch leicht verfälschen. Außerdem geht er von linearen Beziehungen zwischen den Variablen aus und somit kann er bei nichtlinearen Beziehungen zwischen den Variablen die Korrelation sehr verzerren. 
• Datenskalierung: Zusätzlich sollte man vorsichtig sein, wenn man mit Daten arbeitet, die auf unterschiedlichen Skalen arbeiten oder in verschiedenen Einheiten gemessen werden. In solchen Fällen kann die Berechnung der Korrelation beeinträchtigt sein. Deshalb sollte man auf eine Standardisierung oder Normalisierung der Daten zurückgreifen, sodass alle Daten auf einer vergleichbaren Skala liegen. Dafür kann beispielsweise der MinMax Scaler genutzt werden oder es kann der z-Score berechnet werden. 
• Multikollinearität: Eine weitere Herausforderung bei dem Umgang mit der Korrelationsmatrix ist das Problem der Multikollinearität. Dieses tritt dann auf, wenn zwei oder mehr Variablen in einer multivariaten Analyse miteinander korrelieren. Dadurch kann es beispielsweise bei Regressionsanalysen zu verzerrten Parameterschätzungen kommen. 

Die Korrelationsmatrix ist ein mächtiges Werkzeug in der Datenanalyse. Jedoch sollte man sich den Grenzen und Schwachstellen dieser Methode bewusst sein, um sie richtig zu verwenden und belastbare Ergebnisse zu erhalten. 

Das solltest Du mitnehmen

• Die Korrelationsmatrix wird in der Datenanalyse dazu verwendet, um Korrelationen zwischen den Variablen in einem Datensatz zu veranschaulichen. 
• Dabei wird die Korrelation paarweise zwischen den Variablen berechnet und anschließend in einer quadratischen Matrix abgebildet. 
• Neben dem Pearson-Koeffizient können auch andere Korrelationskoeffizienten verwendet werden, die beispielsweise besser für nichtlineare Beziehungen geeignet sind. 
• In den meisten Fällen werden die Ergebnisse der Matrix mithilfe einer Heatmap dargestellt. Dabei deuten häufig dunklere Felder auf eine höhere und hellere Felder auf eine schwächere Korrelation hin. 
• In Python kann die Korrelationsmatrix einfach aus einem DataFrame berechnet und anschließend mithilfe von seaborn veranschaulicht werden. 
• Trotz der Stärken der Korrelationsmatrix sollte man sich der Grenzen dieser Methode bewusst sein. Dazu zählen beispielsweise die Empfindlichkeit gegenüber Ausreißern oder die Problematiken bei unterschiedlichen Skalen. 

Andere Beiträge zum Thema Korrelationsmatrix

Eine Dokumentation über die Erstellung einer Korrelationsmatrix in Scikit-Learn findest Du hier.