Die multivariate Analyse umfasst verschiedene Methoden innerhalb der Statistik, die sich mit der Untersuchung von Daten beschäftigt, bei denen mehrere Variablen gleichzeitig betrachtet werden. In Anwendungsbereichen, wie der Medizin, der Wirtschaft oder den Biowissenschaften, werden immer mehr und komplexere Datensätze erhoben, weshalb die multivariate Analyse in diesen Gebieten unverzichtbar geworden ist. Sie umfasst leistungsfähige Werkzeuge, um Einblicke in die komplexen Zusammenhänge zu gewinnen. 

In diesem Beitrag beschäftigen wir uns mit den Grundlagen der multivariaten Analyse und schauen uns im Detail verschiedene Methoden an, die hierbei verwendet werden. Darunter sind die wichtigsten Methoden, wie zum Beispiel die Hauptkomponentenanalyse, Clustermethoden oder Regressionsmethoden. Anschließend wird die Interpretation der Ergebnisse genauer beleuchtet, damit spezifische Fragestellungen auch ausreichend beantwortet werden können. Zum Abschluss zeigen wir auch die Vor- und Nachteile der multivariaten Analyse auf.   

Was ist die multivariate Analyse?

Die multivariate Analyse umfasst statistische Methoden zur gleichzeitigen Analyse von mehreren Variablen und deren Zusammenhänge. Dadurch wird es möglich, Wechselwirkungen zwischen Variablen zu erkennen, die in einer isolierten Betrachtung unentdeckt geblieben wären. Diese Erkenntnisse werden dann wiederum für das Training von präzisen Vorhersagemodellen genutzt. Durch das simultane Betrachten von mehreren Variablen können nicht nur Korrelationen zwischen einzelnen Merkmalen entdeckt werden, sondern auch zwischen kompletten Merkmalgruppen. Dieses Verständnis hilft bei der Auswahl von Entscheidungsmodellen und dem Aufstellen von Hypothesen. 

Außerdem ermöglicht die multivariate Analyse häufig eine Reduktion der Datenkomplexität, sodass die Informationen des Datensatzes auf weniger Dimensionen komprimiert werden. Diese Eigenschaft ist sehr hilfreich für die Visualisierung der Daten und macht sie zusätzlich noch leichter interpretierbar. 

Die Einsatzmöglichkeiten der multivariaten Analyse sind sehr vielseitig und umfassen zum Beispiel die folgenden Bereiche: 

• Medizin: Die menschliche Gesundheit setzt sich aus vielen Wechselwirkungen zusammen und wird beispielsweise beeinflusst durch den Blutdruck, den Cholesterinspiegel oder genetische Faktoren. Mithilfe der multivariaten Analyse lassen sich alle diese Merkmale in ein Modell bringen und auf diese Weise können Risikofaktoren für Krankheiten identifiziert oder Diagnosen erstellt werden. 
• Biologie: Im Bereich der Genforschung werden multivariate Analysen eingesetzt, um Genfunktionen zu identifizieren und Expressionsmuster zu untersuchen. Durch die Möglichkeit tausende Gene gleichzeitig zu analysieren, können die Forscher Einblicke in die Einflüsse von Genen auf Krankheiten gewinnen. 
• Finanzwesen: Bei der Erstellung von Anlageportfolios spielt das inkludierte Risiko eine große Rolle, um abwägen zu können, ob der Gewinn zum eingegangenen Risiko in einem guten Verhältnis steht. Durch die Bestimmung der Korrelation zwischen den Anlageklassen und verschiedenen Wirtschaftsindikatoren kann das Risiko ausreichend bewertet werden und darauf basierend Investitionsentscheidungen getroffen werden. 

Die multivariate Analyse bietet leistungsfähige Werkzeuge für verschiedenste Anwendungen und die Interpretation der zugrundeliegenden Zusammenhänge. 

Welche Schritte sollten in der Datenvorverarbeitung stattfinden?

Damit die multivariate Analyse möglichst gute Vorhersagen treffen kann, ist es wichtig, dass die Daten sorgfältig aufbereitet werden. Die Datenqualität hat einen nicht zu unterschätzenden Einfluss auf die Fähigkeit des Modells Muster und Zusammenhänge zu erkennen. In diesem Abschnitt gehen wir auf die drei wichtigsten Faktoren ein, die bei der Datenvorverarbeitung beachtet werden sollten. 

Datenqualität

Im Bereich der Datenqualität sollte auf diese Punkte besonders geachtet werden, um eine erfolgreiche multivariate Analyse betreiben zu können: 

• Vollständigkeit: Alle Datenpunkte im Datensatz sollten Werte für alle Variablen aufweisen, sodass es keine fehlenden Werte gibt. Fehlende Daten können dazu führen, dass gewisse Muster nicht erkannt oder deren Einfluss zu gering eingeschätzt wird. Falls doch leere Felder vorhanden sind, sollten diese Datenpunkte, wenn möglich, aus dem Datensatz entfernt werden. Wenn jedoch die Größe des Datensatzes dies nicht zulässt, kann man auch Methoden anwenden, um Werte entsprechend einsetzen zu können. Beispielsweise kann der Mittelwert der Variablen in die fehlenden Felder eingetragen werden. 
• Konsistenz: Die Konsistenz im Datensatz sollte gegeben sein, sodass ähnliche Einträge im Datensatz über den gesamten Datensatz hinweg einheitlich erhoben wurden. Dieser Punkt verhindert, dass Widersprüche im Datensatz entstehen, die die multivariate Analyse verzerren können. Unter diesen Punkt fällt zum Beispiel, dass alle Gewichtsangaben in den Daten mit einer Waage gemessen wurden und nicht ein Teil der Körpergewichte von den Befragten einfach geschätzt werden. 
• Ausreißerbehandlung: Ausreißer sind Werte in einem Datensatz, die außerhalb des normalen Bereichs liegen, die ansonsten im Datensatz vorkommen. Abhängig vom Analyseziel kann entschieden werden, ob die Ausreißer aus dem Datensatz entfernt werden oder transformiert werden sollten. Wichtig ist jedoch, dass man den Datensatz auf Ausreißer untersucht und eine entsprechende Entscheidung trifft. 

Normalisierung & Standardisierung

Viele multivariate Analysemethoden setzen voraus, beziehungsweise liefern bessere Ergebnisse, wenn alle Variablen auf einer vergleichbaren Skala liegen, um die Ergebnisse vergleichbar zu machen. In Datensätzen kann es jedoch schnell dazu kommen, dass die Variablen in unterschiedlichen Wertebereichen und Einheiten vorliegen. Wenn in einer Datenreihe beispielsweise das Körpergewicht gemessen wird, so liegt dies maximal im dreistelligen Bereich. Bei einer gleichzeitigen Abfrage des Jahreseinkommens eines Probanden kann dies jedoch im sechs- oder sogar siebenstelligen Bereich liegen, sodass sich die Wertebereiche zwischen Gewicht und Jahreseinkommen sehr stark unterscheiden. Um diese Werte in einen einheitlichen Rahmen zu bringen, gibt es verschiedene Methoden. 

• Standardisierung: Bei der Standardisierung werden die Werte so transformiert, dass sie einer einheitlichen Datenverteilung folgen, also beispielsweise einen Mittelwert von 0 und eine Standardabweichung von 1 haben. Dies führt dazu, dass die Skala aller Variablen vergleichbar wird, ohne aber, dass die Daten ihre ursprüngliche Verteilung verändern. Bestimmte Methoden der multivariaten Analyse, wie zum Beispiel die Hauptkomponentenanalyse, enthalten verfälschte Ergebnisse, wenn die Daten nicht standardisiert werden. 
• Normalisierung: Die Normalisierung hingegen, bringt die Daten lediglich auf einen gemeinsamen Wertebereich, beispielsweise zwischen 0 und 1, verändert dabei jedoch die Verteilung der Daten. Eine häufige Form der Normalisierung ist es, alle Werte durch den Maximalwert der Variablen zu teilen, sodass die Daten (wenn keine negativen Werte vorhanden sind) anschließend im Bereich zwischen 0 und 1 liegen. 

Datenbereinigung

Die Datenbereinigung umfasst verschiedene Schritte, die dazu dienen, einen möglichst vollständigen und fehlerfreien Datensatz zu erstellen. Die genutzten Methoden sind stark von den Variablen und Werten abhängig und können beispielsweise die folgenden Punkte enthalten. 

• Verzerrungen korrigieren: Verzerrungen sind systematische Fehler in der Datenerhebung, welche zum Beispiel entstehen können, wenn gewisse Gruppen im Datensatz überrepräsentiert sind im Vergleich zur gesamten Population. Um diese zu korrigieren, gibt es verschiedene Methoden, wie das Resampling oder die Nutzung von Gewichtungen für bestimmte Datenpunkte. Dadurch wird eine repräsentative Datenbasis für die multivariate Analyse geschaffen. 
• Vereinheitlichung: In diesem Schritt werden die Variablen auf eine gemeinsame Einheit gebracht, falls die Werte in unterschiedlichen Einheiten erhoben wurden. Dadurch ist die Vergleichbarkeit der Werte untereinander deutlich höher. 
• Umgang mit fehlenden Werten: Wenn im Bereich der Datenqualität erkannt wurde, dass unvollständige Daten vorliegen, dann sollten diese während der Datenbereinigung behoben werden. Gängige Methoden dafür sind beispielsweise das Löschen des gesamten Datenpunktes oder die Schätzung der fehlenden Werte auf Basis der anderen, vorhandenen Werte der Variablen. 

Was sind die wichtigsten Methoden in der multivariaten Analyse?

Die multivariate Analyse umfasst eine breite Palette an Methoden und Algorithmen zum Erlernen von komplexen Beziehungen und Strukturen aus Daten. Dabei werden zwei große Bereiche unterschieden: 

1. Strukturentdeckende Methoden: Die Algorithmen in dieser Gruppe beschäftigen sich damit, neue Zusammenhänge und Muster im Datensatz zu finden, ohne dass diese vom Anwender vorgegeben werden. Sie können also vor allem dann genutzt werden, wenn es noch keine Hypothesen gibt, welche Abhängigkeiten zwischen Variablen oder Objekten bestehen könnten. Abhängig von der jeweiligen Quelle spricht bei den strukturentdeckenden Methoden auch von explorativen Methoden. 
2. Strukturprüfende Methoden: Die strukturprüfenden Methoden hingegen beschäftigen sich mit der Analyse und Überprüfung von konkret vorgegebenen Zusammenhängen in einem Datensatz. Sie können dabei helfen, konkrete Hypothesen des Anwenders zu testen und belastbare Ergebnisse dafür zu liefern. In verschiedenen Quellen ist dabei auch von induktiven Methoden die Rede. 

In den folgenden Abschnitten erklären wir die wichtigsten Methoden in diesen beiden Teilbereichen. 

Strukturentdeckende Verfahren

Strukturentdeckende Verfahren sind besonders nützlich, wenn noch keine Hypothese über die Daten bekannt ist und dadurch keine Vorgaben zu möglichen Zusammenhängen gemacht werden kann. Die folgenden Methoden schaffen es eigenständig Strukturen und Muster zu erkennen, ohne dass der Nutzer Eingaben tätigen muss. 

Hauptkomponentenanalyse

Viele Machine Learning Modelle haben Probleme mit vielen Eingabevariablen, da diese zum sogenannten Fluch der Dimensionalität führen können. Damit wird eine Vielzahl von Problemen beschrieben, die auftreten, wenn einem Datensatz mehr Merkmale hinzugefügt werden. Außerdem gibt es Modelle, wie beispielsweise die Lineare Regression, die empfindlich auf korrelierte Eingabevariablen reagiert. Deshalb kann es sinnvoll sein, die Zahl der Merkmale in der Datenvorverarbeitung zu verringern. Jedoch muss sichergestellt sein, dass so wenige Informationen wie möglich bei diesem Schritt verloren gehen. 

Die Hauptkomponentenanalyse geht davon aus, dass mehrere Variablen in einem Datensatz möglicherweise dasselbe messen, also korreliert sind. Diese verschiedenen Dimensionen können mathematisch zu sogenannten Hauptkomponenten zusammengefügt werden ohne, dass die Aussagekraft des Datensatzes darunter leidet. Die Schuhgröße und die Körpergröße beispielsweise sind häufig korreliert und können deshalb von einer gemeinsamen Dimension ersetzt werden, um die Zahl der Eingabevariablen zu verringern. 

Die Hauptkomponentenanalyse, oder englisch Principal Component Analysis (kurz: PCA), beschreibt ein Verfahren, wie diese Komponenten mathematisch berechnet werden kann. Die folgenden beiden Schlüsselkonzepte sind dabei zentral: 

Die Kovarianzmatrix ist eine Matrix, die die paarweisen Kovarianzen zwischen zwei verschiedenen Dimensionen des Datenraums angibt. Es handelt sich um eine quadratische Matrix, die also genauso viele Zeilen wie Spalten besitzt. Für zwei beliebige Dimensionen errechnet sich die Kovarianz wie folgt: 

\(\)\[Cov\left(X,\ Y\right)= \frac{\sum_{i=1}^{n}{\left(X_i-\bar{X}\right)\cdot(Y_i-\bar{Y})}}{n-1}\]

Hierbei steht \(n\) für die Anzahl der Datenpunkte im Datensatz,  \(X_i\) ist der Wert der Dimension \(X\) des \(i\)-ten Datenpunkts und \(\bar{X}\) ist der Mittelwert der Dimension \(X\) für alle \(n\) – Datenpunkte. Die Kovarianzen zwischen zwei Dimensionen hängen, wie man an der Formel sehen kann, nicht von der Reihenfolge der Dimensionen ab, sodass gilt: \(COV(X,Y) = COV(Y,X)\). Aus diesen Werten ergibt sich die folgende Kovarianzmatrix \(C\) für die zwei Dimensionen \(X\) und \(Y\):

\(\)\[C=\left[\begin{matrix}Cov(X,X)&Cov(X,Y)\\Cov(Y,X)&Cov(Y,Y)\\\end{matrix}\right]\]

Die Kovarianz aus zwei identischen Dimensionen ist dabei einfach die Varianz der Dimension selbst, also: 

\(\)\[C=\left[\begin{matrix}Var(X)&Cov(X,Y)\\Cov(Y,X)&Var(Y)\\\end{matrix}\right]\]

Die Kovarianzmatrix ist der erste wichtige Schritt in der Hauptkomponentenanalyse. Nachdem diese Matrix erstellt wurde, können daraus die Eigenwerte und Eigenvektoren berechnet werden. Mathematisch gesehen wird für die Eigenwerte die folgende Gleichung gelöst:

\(\)\[\det{\left(C-\ \lambda I\right)}=0\]

Hierbei ist \(\lambda\) der gesuchte Eigenwert und \(I\) die Einheitsmatrix in derselben Größe wie die Kovarianzmatrix \(C\). Wenn diese Gleichung gelöst wird, erhält man einen oder mehrere Eigenwerte einer Matrix. Sie stellen die lineare Transformation der Matrix in Richtung des zugehörigen Eigenvektors dar. Zu jedem Eigenwert kann also auch ein zugehöriger Eigenvektor berechnet werden, wofür die leicht abgewandelte Gleichung gelöst werden muss: 

\(\)\[\left(A-\ \lambda I\right)\cdot v=0\]

Wobei \(v\) der gesuchte Eigenvektor ist, nach dem die Gleichung entsprechend aufgelöst werden muss. Im Falle der Kovarianzmatrix entspricht der Eigenwert der Varianz des Eigenvektors, der wiederum eine Hauptkomponente darstellt. Jeder Eigenvektor ist also eine Mischung verschiedener Dimensionen des Datensatzes, die Hauptkomponenten. Der dazugehörige Eigenwert gibt also an, wie viel Varianz des Datensatzes durch den Eigenvektor erklärt wird. Umso höher dieser Wert, umso wichtiger ist die Hauptkomponente, da sie einen Großteil der Information des Datensatzes enthält. 

Deshalb werden nach Berechnung der Eigenwerte diese der Größe nach sortiert und die Eigenwerte mit den höchsten Werten werden ausgewählt. Anschließend werden die dazugehörigen Eigenvektoren berechnet und als Hauptkomponenten genutzt. Dadurch wird eine Dimensionsreduktion herbeigeführt, da statt der einzelnen Merkmale des Datensatzes nur die Hauptkomponenten zum Training des Modells genutzt werden. 

Für eine weiterführende Erklärung zur Hauptkomponentenanalyse und einem Beispiel, wie man den Algorithmus in Python umsetzen kann, schaue dir gerne unseren detaillierten Artikel dazu an. 

Faktorenanalyse

Die Faktorenanalyse ist eine weitere Methode, die es zum Ziel hat, die Anzahl der Dimensionen in einem Datensatz zu reduzieren. Das Ziel ist es hierbei latente, also nicht direkt beobachtbare Variablen zu finden, die die Korrelation zwischen beobachtbaren Variablen in einem Datensatz erklären. Diese latenten Variablen, welche als Faktoren bezeichnet werden, repräsentieren zugrundeliegende Dimensionen, welche die Datenstruktur deutlich vereinfachen. Diese Analyse ist vor allem im Bereich der Psychologie weit verbreitet, da es hier viele latente Faktoren, wie beispielsweise „Teamfähigkeit“ oder „Empathie“ gibt, welche nicht direkt gemessen werden können, sondern durch beobachtbare Fragen, wie zum Beispiel „Arbeitest Du gerne in Gruppen?“ herausgefunden werden müssen. 

Um die Methodik der Faktorenanalyse genauer verstehen zu können, betrachten wir den folgenden psychologischen Persönlichkeitstest, welcher diese Aussagen umfasst: 

1. Ich genieße es, mit anderen Menschen zu reden.
2. Ich fühle mich wohl in großen Gruppen. 
3. Ich mag es, neue Leute kennenzulernen. 
4. Ich arbeite gerne alleine. 
5. Ich genieße ruhige Umgebungen. 

Diese Aussagen wollen wir nun in möglichst wenige latente Faktoren zerlegen, die noch einen Großteil der Korrelation zwischen den Variablen erklären. Angenommen wir erhalten für unseren Datensatz die folgende Korrelationsmatrix, welche die paarweisen Korrelationen zwischen den gestellten Fragen verdeutlichen. 

	Frage 1	Frage 2	Frage 3	Frage 4	Frage 5
Frage 1	1.00	0.80	0.75	-0.40	-0.50
Frage 2	0.80	1.00	0.85	-0.30	-0.40
Frage 3	0.75	0.85	1.00	-0.35	-0.45
Frage 4	-0.40	-0.30	-0.35	1.00	0.70
Frage 5	-0.50	-0.40	-0.45	0.70	1.00

Aus dieser Korrelationsmatrix können wir bereits erkennen, dass es zwei Lager an Fragen gibt, also möglicherweise zwei Faktoren vorliegen. Die Fragen 1-3 weisen alle untereinander eine positive Korrelation auf, während sie zu den Fragen 4 und 5 eine negative Korrelation aufweisen. Diese Fragen können wir möglicherweise einem gemeinsamen Faktor „Geselligkeit“ zuordnen. Für die Fragen 4 und 5 ist dieses Verhalten genau umgekehrt und sie könnten dem Faktor „Inversion“ zugewiesen werden. Um für diese Annahmen belastbare, mathematische Ergebnisse zu errechnen, durchlaufen wir die folgenden Schritte der Faktorenanalyse: 

1. Berechnung der Kommunalität

Mit der Hilfe der Korrelationsmatrix können wir im ersten Schritt die Anzahl der Faktoren bestimmen. Dazu berechnen wir die Eigenwerte der Matrix, wobei es für jede Variable genau einen Eigenwert gibt. Für unsere Korrelationsmatrix erhalten wir die folgenden Eigenwerte: 

\(\)\[\lambda_1\approx\ 3.23;\ \lambda_2\approx\ 1.09;\ \lambda_3\approx\ 0.29;\ \lambda_4\approx\ 0.25;\ \lambda_5\approx0.14\]

Nach dem sogenannten Kaiser-Kriterium werden nur die Eigenwerte mit einem Wert größer als 1 als Faktoren extrahiert. Nach dieser Regel erhalten wir also, wie vermutet, zwei Faktoren. 

Für diese beiden Faktoren können wir nun die sogenannten Faktorladungen bestimmen, also wie hoch die Korrelation der Variablen mit einem Faktor ist. Diesen Kennwert benötigen wir zur weiteren Berechnung der Kommunalität und wir erhalten es, indem wir eine Matrix bilden mit den beiden Eigenvektoren als Spaltenvektoren und die erste Spalte mit der Wurzel des ersten Eigenwerts und die zweite Spalte mit der Wurzel des zweiten Eigenwerts multiplizieren. Dadurch erhalten wir die folgende Faktorladungsmatrix:

\(\)\[E = \begin{bmatrix} 0.4906 & 0.6131 \\ 0.4815 & 0.3298 \\ 0.4859 & -0.1949 \\
-0.3561 & 0.6474 \\ -0.4058 & 0.2294 \end{bmatrix}\]

Mithilfe von dieser Matrix können schließlich die Kommunalitäten berechnet werden, welche eine Aussage darüber geben, wie viel der Varianz von einer Variablen durch die beiden Faktoren abgebildet wird. Dafür werden zeilenweise die quadrierten Elemente in jeder Zeile aufsummiert. 

Für die erste Variable ergibt sich dann beispielsweise: 

\(\)\[h_1^2\ =\ \left(0.4906\right)^2\ +\ \left(0.6131\right)^2\ =\ 0.617 \]

Dies bedeutet, dass etwa 61% der Varianz der ersten Variablen durch die beiden Faktoren erklärt wird. Die restliche Varianz geht durch die Reduzierung der Dimensionalität verloren. 

2. Rotation der Faktoren

Die Rotation der Faktoren ist ein wichtiger Schritt in der Faktorenanalyse bei dem die Interpretierbarkeit der Faktoren erhöht werden soll. Das Problem mit dem aktuellen Ergebnis ist, dass die lineare Kombination der fünf Variablen pro Faktor nur sehr schwierig zu veranschaulichen und zu interpretieren ist. Das Ziel der Rotation ist es nun die Faktorladungen so zu verändern, dass jede Variable nur möglichst stark auf einen Faktor lädt und möglichst schwach auf die übrigen Faktoren. Dadurch werden die Faktoren klarer abtrennbar. 

Ein häufig genutzter Algorithmus für die Rotation ist der sogenannte Varimax-Algorithmus, bei dem darauf abgezielt wird, dass man die Faktoren so dreht, dass die Varianz der Ladungen maximiert wird. Dadurch lädt jede Variable nur sehr stark auf einen Faktor und die Interpretierbarkeit wird vereinfacht. Dafür ergibt sich dann die folgende Rotationsmatrix:

\(\)\[
E_{\text{rot}} =
\begin{bmatrix}
0.778 & 0.110 \\
0.577 & -0.090 \\
0.220 & -0.475 \\
0.185 & 0.715 \\
-0.138 & 0.445 \\
\end{bmatrix}
\]

3. Interpretation der Faktoren

Basierend auf den rotierten Faktorladungen erkennen wir, wie bereits vor der Analyse angenommen hatten, dass die ersten drei Fragen unter dem ersten Faktor zusammengefasst werden können, welcher im weitesten Sinne die Geselligkeit des Probands misst, also die Bereitschaft und das Interesse mit anderen Menschen zu interagieren. Der zweite Faktor hingegen misst die sogenannte Introversion mit den Fragen 4 und 5, also die Präferenz für Ruhe und alleinige Aktivitäten. 

Die Faktorenanalyse und die Hauptkomponentenanalyse werden oft fälschlicherweise miteinander in Verbindung gebracht, da sie beide der Dimensionsreduktion dienen und eine ähnliche Vorgehensweise besitzen. Jedoch beruhen sie auf unterschiedlichen Annahmen und verfolgen auch unterschiedliche Ziele. Bei der Faktorenanalyse wird versucht, latente, also unbeobachtete Variablen zu finden, welche die Korrelation zwischen den Variablen erklären. Die Hauptkomponentenanalyse versucht die Dimensionalität zu reduzieren, indem die Maximierung der Varianz angestrebt wird. 

Dadurch unterscheiden sich auch die Anwendungen deutlich, da die Hauptkomponentenanalyse vor allem für die Datenvisualisierung und die Clusterbildung verwendet wird, also als erster Schritt für eine weitere Analyse dient. Die Faktorenanalyse hingegen werden in Bereichen genutzt, in denen latente Strukturen erkannt werden sollen, wie beispielsweise der Psychologie oder der Intelligenzforschung. 

Clusteranalyse

Die Clusteranalyse umfasst verschiedene Methoden innerhalb der explorativen Analyse, welche darauf abzielen, die Datenpunkte in einem Datensatz einem Cluster oder einer Gruppe zuzuordnen, sodass alle Mitglieder einer Gruppe möglichst ähnlich zueinander sind und möglichst unterschiedlich zu den anderen Gruppen. Es zählt zu den unüberwachten Lernverfahren, da keine vordefinierten Labels oder Kategorien gegeben sein müssen. Das k-Means Clustering ist dabei die wahrscheinlich populärste Methode, um den Datensatz in k verschiedene Gruppen zu unterteilen. 

Dabei wird iterativ versucht, eine optimale Clusterzuordnung von k-Gruppen zu finden. Das wichtigste Merkmal ist hierbei, dass die Anzahl der Cluster bereits im Vorhinein bestimmt werden muss und sich nicht erst im Laufe des Trainings ergibt. Der Buchstabe k steht hierbei repräsentativ für die gesuchte Anzahl von Gruppen. 

Wenn diese Anzahl festgelegt ist, werden die folgenden Schritte als Teil des Algorithmus ausgeführt: 

1. Wahl von k: Bevor der Algorithmus starten kann, muss die Anzahl der gesuchten Cluster bestimmt werden. 
2. Initialisierung: Während der Initialisierung werden k zufällige Datenpunkte erstellt. Diese dienen als anfängliche Clusterzentren und müssen nicht Teil des Datensatzes sein. Der Verlauf des Clusterings kann maßgeblich von der Wahl des Initialisierungsverfahrens abhängen, weshalb wir uns zu einem späteren Zeitpunkt noch genauer damit beschäftigen. 
3. Zuordnung aller Datenpunkte zu einem Cluster: Alle Datenpunkte im Datensatz werden dem naheliegendsten Clusterzentrum zugewiesen. Dabei wird für jeden Punkt die Distanz zu allen Zentren errechnet und der Gruppe zugeordnet, die die geringste Distanz aufweist. 
4. Update der Clusterzentren: Nachdem alle Punkte einer Gruppe zugeordnet wurden, werden für jedes Cluster neue Zentren berechnet. Dazu werden alle Punkte einer Gruppe zusammengefasst und der Durchschnitt der Merkmale berechnet. Dadurch ergeben sich k neue oder auch gleichbleibende Clusterzentren.
5. Wiederholung bis zur Konvergenz: Die Schritte drei und vier werden so lange ausgeführt bis sich die Clusterzentren nicht oder nur noch sehr wenig verändern. Dadurch kommt es zur Konvergenz und die Zuordnung von Datenpunkten zu einer Gruppe verändert sich nicht mehr. 

Für einen noch tieferen Einblick in das k-Means Clustering, empfehlen wir dir unseren detaillierten Artikel zu diesem Thema.

Strukturprüfende Verfahren

Die strukturprüfenden Verfahren innerhalb der multivariaten Analyse untersuchen vorgegebene Hypothesen und Annahmen über einen Datensatz und liefern dafür konkrete Werte. Die Methoden unterscheiden sich vor allem darin, wie sie den Zusammenhang zwischen Variablen modellieren.  

Regressionsanalyse

Regressionen sind ein zentraler Bestandteil im Bereich der multivariaten Analyse, welche es ermöglichen, den Einfluss mehrerer sogenannter unabhängiger Variablen auf eine oder mehrere sogenannte abhängige Variablen abzuschätzen. Sie zählen zu den strukturprüfenden Verfahren, da vor der Analyse festgelegt werden muss, welche unabhängigen Variablen genutzt werden, um eine Vorhersage für eine abhängige Variable zu treffen. Über die Zeit haben sich unterschiedliche Methoden gebildet, welche sich in der zugrundeliegenden Modellierung unterscheiden. 

Multiple Regression

Die multiple Regression ist eine Erweiterung im Vergleich zur linearen Regression bei der mehr als eine unabhängige Variable genutzt wird, um die abhängige Variable vorherzusagen. Mithilfe der Trainingsdaten wird versucht für die folgende Gleichung möglichst aussagekräftige Werte für die Regressionskoeffizienten zu finden, die dann wiederum genutzt werden können, um neue Vorhersagen zu treffen: 

\(\)\[Y\ =\ \beta_0\ +\ \beta_1X_1\ +\ \ldots\ +\ \beta_pX_p\ +\ \varepsilon \]

Hierbei sind: 

• \( Y \) ist die abhängige Variable, die vorhergesagt werden soll. 
• \( X_1, … , X_p\) sind die unabhängigen Variablen, deren Werte aus dem Datensatz kommen. 
• \( \beta_0 \) ist der Achsenabschnitt, also der Schnittpunkt der Regressionsgeraden mit der y-Achse. 
• \( \beta_1, …, \beta_p \) sind die Regressionskoeffizienten, also der Einfluss, den diese unabhängige Variable auf die Vorhersage der abhängigen Variable hat. 
• \( \epsilon \) ist der Fehlerterm, welcher alle Einflüsse einschließt, welche nicht durch die unabhängigen Variablen erklärt werden können. 

Mithilfe eines iterativen Trainings wird dann versucht, die Regressionskoeffizienten zu finden, welche am besten die abhängige Variable vorhersagen können. Dafür wird häufig die Ordinary Least Squares Methode als Fehlerfunktion eingesetzt. Eine große Herausforderung bei der multiplen Regression ist die sogenannte Multikollinearität, welche dazu führen kann, dass die Stabilität der Koeffizienten leidet. Deshalb sollten vor dem Training weitreichende Untersuchungen zur Korrelation zwischen den Variablen stattfinden. 

Logistische Regression

Die logistische Regression ist eine spezielle Form der Regressionsanalyse, die genutzt wird, wenn die abhängige, also die vorherzusagende, Variable, nur eine bestimmte Anzahl an möglichen Werten annehmen kann. Man spricht dann auch davon, dass diese Variable nominal- bzw. ordinalskaliert ist. Die logistische Regression liefert uns als Ergebnis eine Wahrscheinlichkeit, mit der der Datensatz einer Klasse zuzuordnen ist.

Bei der linearen Regression haben wir versucht einen konkreten Wert für die abhängige Variable vorherzusagen, statt eine Wahrscheinlichkeit auszurechnen, mit der die Variable einer bestimmten Klasse angehört. Beispielsweise haben wir versucht die konkrete Klausurnote eines Studenten zu bestimmen, abhängig von den Stunden, die der Student für das Fach gelernt hat. Die Grundlage für die Schätzung des Modells ist die Regressionsgleichung und entsprechend auch der Graph, der sich daraus ergibt. 

Wir wollen nun aber ein Modell aufbauen, das uns die Wahrscheinlichkeit vorhersagt, dass eine Person ein E-Bike kauft, abhängig von ihrem Alter. Nachdem wir ein paar Probanden befragt haben, erhalten wir folgendes Bild:

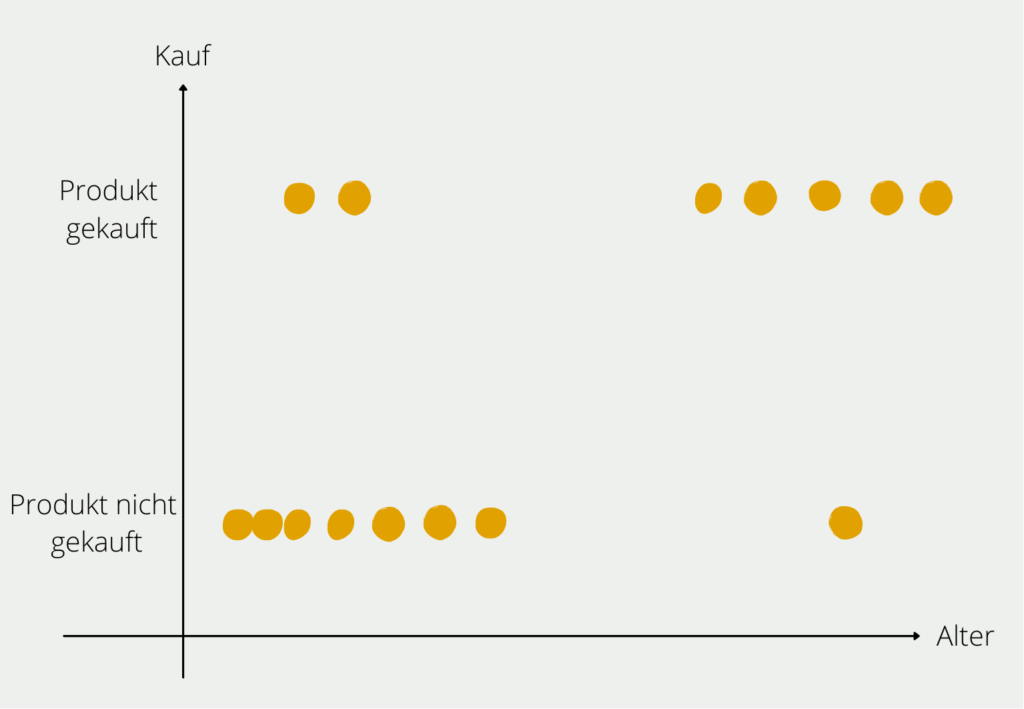
Aus unserer kleinen Probandengruppe können wir die Verteilung erkennen, dass junge Personen größtenteils kein E-Bike gekauft haben (unten links im Diagramm) und vor allem ältere Menschen sich ein E-Bike kaufen (oben rechts im Diagramm). Natürlich gibt es in beiden Altersschichten auch Ausreißer, aber der Großteil der Befragten entspricht der Regel, dass mit steigendem Alter die Wahrscheinlichkeit wächst, dass man sich ein E-Bike zulegt. Diese Regel, die wir in den Daten erkannt haben, wollen wir nun auch mathematisch belegen. 

Dazu müssen wir eine Funktion finden, die möglichst nahe an der Punkteverteilung, die wir im Diagramm sehen, liegt und zusätzlich nur Werte zwischen 0 und 1 annimmt. Somit fällt eine lineare Funktion, wie wir sie bei der linearen Regression genutzt haben bereits raus, da diese im Bereich zwischen -∞ und +∞ liegt. Jedoch gibt es eine andere mathematische Funktion, die unseren Anforderungen entspricht: die Sigmoid Funktion.

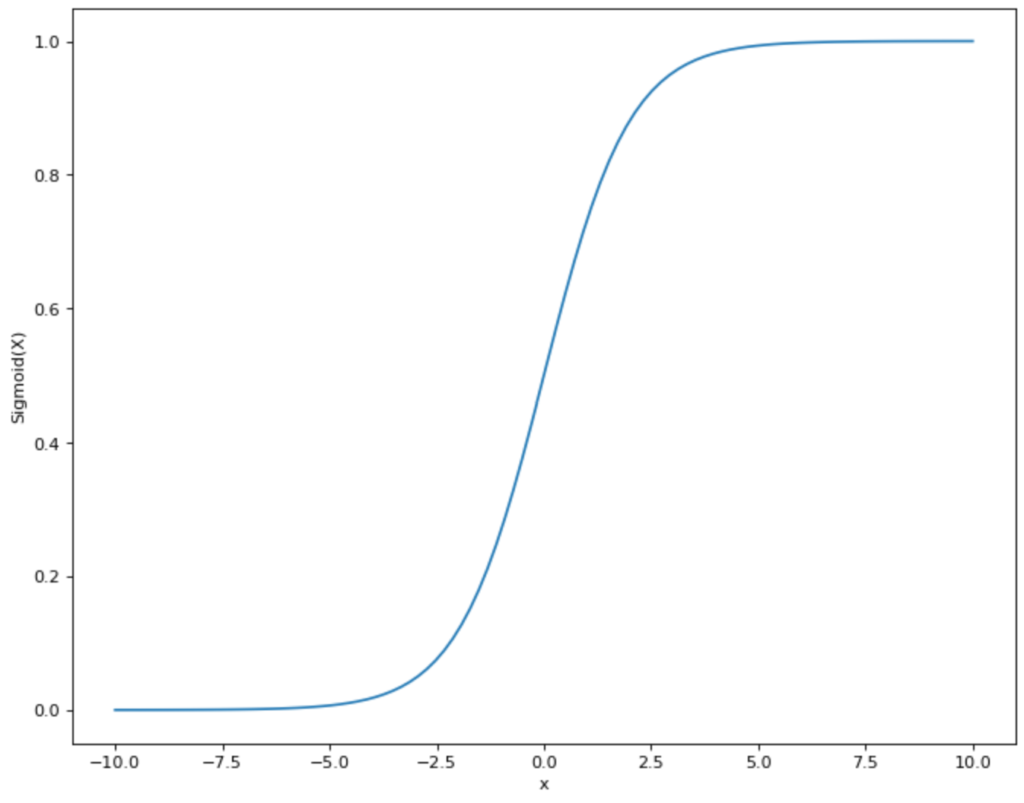
Die Funktionsgleichung des Sigmoid Graphen sieht folgendermaßen aus:

\(\) \[S(x) = \frac{1}{1+e^{-x}}\]

Oder für unser Beispiel:

\(\) \[P(\text{Kauf E-Bike})) = \frac{1}{1+e^{-(a + b_1 \cdot \text{Alter})}}\]

Damit haben wir eine Funktion, die uns als Ergebnis die Wahrscheinlichkeit des E-Bike Kaufs liefert und als Variable das Alter der Person nutzt. Der Graph würde dann für unser Beispiel in etwa so aussehen: 

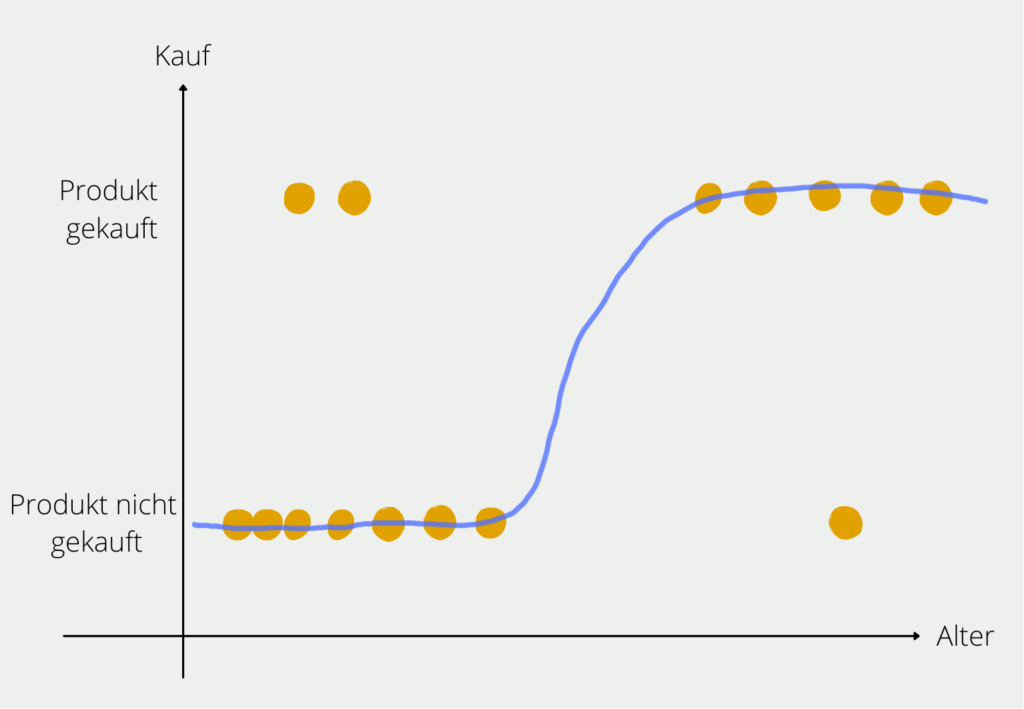
In der Praxis sieht man häufig nicht die Schreibweise, die wir genutzt haben. Stattdessen stellt man die Funktion so um, dass die eigentliche Regressionsgleichung deutlich wird:

\(\) \[logit(P(\text{Kauf E-Bike}) = a + b_1 \cdot \text{Alter}\]

Ridge- und Lasso-Regression 

Bei einer hohen Anzahl von unabhängigen Variablen entsteht schnell eine erhöhte Gefahr von Overfitting, da das Modell zu viele Regressionsparameter besitzt und deshalb das Risiko steigt, dass es Strukturen aus dem Trainingsdatensatz einfach auswendig lernt. Deshalb haben sich die folgenden beiden Unterformen der Regression gebildet, welche bereits Regularisierungsmethoden beinhalten, die dazu führen sollen, dass die Überanpassung verhindert wird. 

L1 – Regularisierung (Lasso)

Die L1-Regularisierung, oder auch Lasso (Least Absolute Shrinkage and Selection Operator), verfolgt das Ziel, die absolute Summe aller Netzwerkparameter zu minimieren. Dadurch wird das Modell also bestraft, wenn die Größe der Parameter zu stark ansteigt. Durch dieses Vorgehen kann es bei der L1-Regularisierung dazu kommen, dass einzelne Modellparameter auf null gesetzt werden, wodurch bestimmte Merkmale im Datensatz nicht mehr beachtet werden. Dadurch entsteht ein kleineres Modell mit weniger Komplexität, welches nur die wichtigsten Merkmale für die Vorhersage umfasst. 

Mathematisch gesehen, wird ein weiterer Term in die Kostenfunktion hinzugefügt. In unserem Beispiel gehen wir von einer Verlustfunktion mit einem Mean Squared Error aus, bei dem die durchschnittliche, quadrierte Abweichung zwischen dem tatsächlichen Wert aus dem Datensatz und der Vorhersage errechnet wird. Umso geringer diese Abweichung, umso besser ist das Modell darin, möglichst genaue Vorhersagen zu treffen. 

Für ein Modell mit dem Mean Squared Error als Verlustfunktion und einer L1-Regularisierung ergibt sich dann die folgende Kostenfunktion: 

\(\) \[J\left(\theta\right)=\frac{1}{m}\sum_{i=1}^{m}\left(y_i-\widehat{y_i}\right)^2+\lambda\sum_{j=1}^{n}\left|\theta_j\right|\]

• \(J\) ist die Kostenfunktion. 
• \(\lambda\) ist der Regularisierungsparameter, der mitbestimmt, wie stark die Regularisierung einen Einfluss auf den Fehler des Modells hat.
• \(\sum_{j=1}^{n}\left|\theta_j\right|\) ist die Summe aller Parameter des Modells.

Das Ziel des Modells ist es, diese Kostenfunktion zu minimieren. Wenn also die Summe der Parameter anwächst, dann steigt die Kostenfunktion und es gibt einen Anreiz, dem entgegenzuwirken. \(\lambda\) kann dabei jeden positiven Wert (>= 0) annehmen. Ein Wert nahe 0 steht dabei für eine weniger starke Regularisierung, während ein großer Wert für eine starke Regularisierung steht. Mithilfe von beispielsweise der Cross-Validation können verschiedene Modell mit unterschiedlich starker Regularisierung getestet werden, um das optimale Gleichgewicht, abhängig von den Daten, zu finden.

Vorteile der L1 – Regularisierung:

• Merkmalsauswahl: Dadurch, dass das Modell dafür incentiviert wird, die Größe der Parameter nicht zu stark ansteigen zu lassen, werden ein paar der Parameter auch gleich 0 gesetzt. Dadurch werden gewisse Merkmale aus dem Datensatz entfernt und es findet automatisch eine Auswahl der wichtigsten Merkmale statt.
• Einfachheit: Ein Modell mit weniger Merkmalen kann einfacher verstanden und interpretiert werden. 

Nachteile der L1 – Regularisierung: 

• Probleme bei korrelierten Variablen: Wenn mehrere Variablen in dem Datensatz miteinander korreliert sind, neigt Lasso dazu, nur eine der Variablen zu behalten und die anderen, korrelierten Variablen auf null zu setzen. Dadurch können Informationen verloren gehen, welche in den anderen Variablen vorhanden gewesen wären. 

L2 – Regularisierung (Ridge)

Die L2 – Regularisierung versucht dem Problem von Lasso, also dem Entfernen von Variablen, die noch Informationen enthalten, dadurch zu begegnen, dass das Quadrat der Parameter als Regularisierungsterm verwendet wird. Somit fügt sie dem Modell eine Strafe hinzu, die proportional zu dem Quadrat der Parameter ist. Dies hat zur Folge, dass die Parameter nicht komplett auf null gehen, sondern lediglich kleiner werden. Umso näher ein Parameter mathematisch gesehen der Null kommt, umso kleiner wird sein quadrierter Einfluss auf die Kostenfunktion. Deshalb konzentriert sich das Modell vorher auf andere Parameter, bevor es einen Parameter nahe null komplett streicht. 

Mathematisch gesehen sieht die Ridge Regularisierung für ein Modell mit dem Mean Squared Error als Verlustfunktion wie folgt aus: 

\(\)\[J\left(\theta\right)=\frac{1}{m}\sum{\left(i=1\right)^m\left(y_i-\widehat{y_i}\right)^2}+\lambda\sum_{j=1}^{n}{\theta_j^2}\]

Die Parameter sind dabei identisch zu der vorherigen Formel mit dem Unterschied, dass nicht der absolute Wert \(\theta\) aufsummiert wird, sondern das Quadrat. 

Vorteile der L2 – Regularisierung:

• Stabilisierung: Durch die Ridge Regularisierung wird dafür gesorgt, dass die Parameter deutlich stabiler auf kleine Änderungen in den Trainingsdaten reagieren.  
• Handhabung von Multikollinearität: Bei mehreren, korrelierten Variablen sorgt die L2 – Regularisierung dafür, dass diese gemeinsam betrachtet werden und nicht lediglich eine Variable im Modell behalten wird, während die anderen rausgeworfen werden. 

Nachteile der L2 – Regularisierung:

• Keine Merkmalsauswahl: Dadurch, dass Ridge die Parameter nicht auf null setzt, bleiben alle Merkmale aus dem Datensatz im Modell erhalten, wodurch die Interpretierbarkeit schlechter ist, da mehr Variablen berücksichtigt werden.

Künstliche Neuronale Netzwerke

Künstliche Neuronale Netzwerke (KNN) sind leistungsfähige Tools zur Modellierung von komplexen Beziehungen in Datensätzen mit vielen Variablen. Auch hierbei muss zuerst definiert werden, welche Variable oder welche Variablen vorhergesagt werden sollen und welche als Input für die Vorhersage verwendet werden. Deshalb zählen die neuronalen Netzwerke auch zu den strukturprüfenden Methoden. Sie orientieren sich am biologischen Aufbau des menschlichen Gehirns. Damit werden computerbasiert schwierige Problemstellungen und mathematische Berechnungen modelliert und gelöst.

In unserem Gehirn werden die aufgenommenen Informationen der Sinnesorgane in sogenannten Neuronen aufgenommen. Diese verarbeiten die Information und geben anschließend einen Output weiter, der zu einer Reaktion des Körpers führt. Die Informationsverarbeitung findet dabei nicht nur in einem einzelnen Neuron statt, sondern in einem vielschichtigen Netzwerk von Knoten. 

Im Künstlichen Neuronalen Netzwerk wird dieses biologische Prinzip nachgestellt und mathematisch ausgedrückt. Das Neuron (auch Knoten oder Unit genannt) verarbeitet einen oder mehrere Inputs und errechnet daraus einen einzigen Output. Dabei werden drei Schritte ausgeführt:

1. Die verschiedenen Inputs \(x\) werden mit einem Gewichtsfaktor \(w\) multipliziert: 

\(\) \[x_1 \rightarrow x_1 \cdot w_1, x_2 \rightarrow x_2 \cdot w_2 \]

Die Gewichtsfaktoren entscheiden darüber, wie wichtig ein Input für das Neuron ist, um die Problemstellung lösen zu können. Wenn ein Input sehr wichtig, wird der Wert für den Faktor \(w\) größer. Ein unwichtiger Input hat einen Wert von 0.

2. Alle gewichteten Inputs des Neurons werden aufsummiert. Zusätzlich wird noch ein Bias \(b\) hinzugefügt: 

\(\) \[(x_1 \cdot w_1) + (x_2 \cdot w_2) + b \]

3. Anschließend wird das Ergebnis in eine sogenannte Aktivierungsfunktion gegeben. 

\(\) \[y = f((x_1 \cdot w_1) + (x_2 \cdot w_2) + b) \]

Es gibt verschiedene Aktivierungsfunktionen, die genutzt werden können. In vielen Fällen handelt es sich um die Sigmoid Funktion. Diese nimmt Werte und bildet sie im Bereich zwischen 0 und 1 ab:

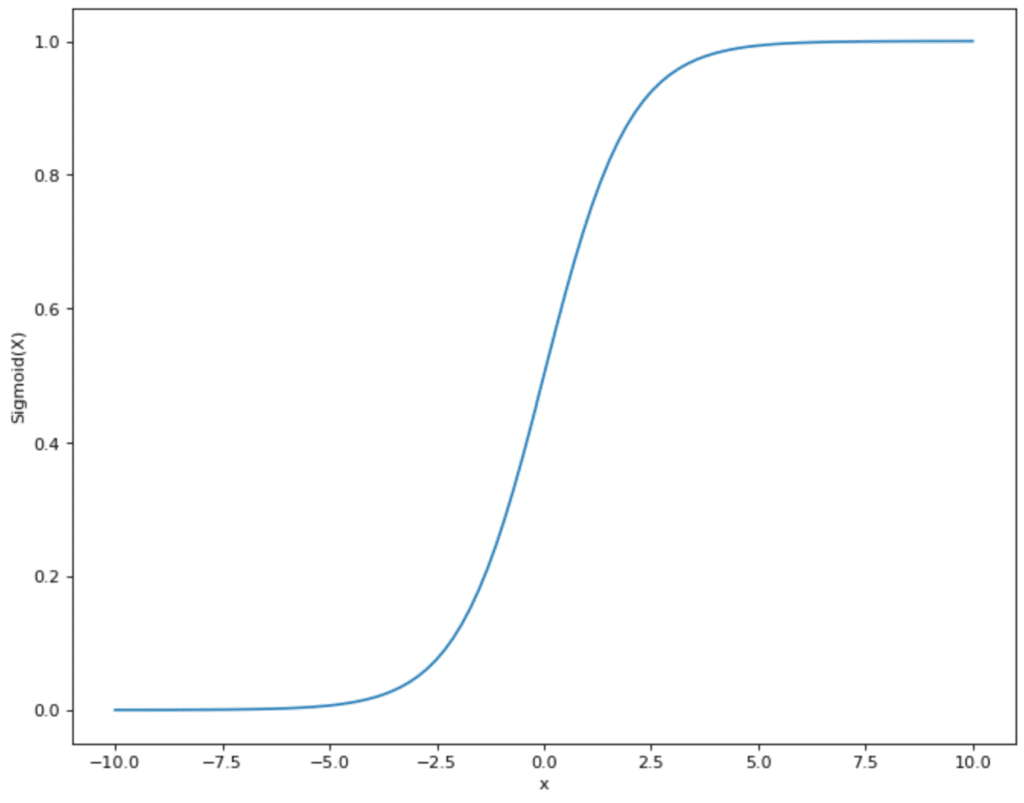
Das hat den Vorteil für das Neuronale Netzwerk, dass alle Werte, die aus Schritt 2 kommen, sich in einem vorgegebenen kleineren Rahmen bewegen. Die Sigmoid Funktion schränkt also Werte ein, die theoretisch zwischen (- ∞, + ∞) liegen können, und bildet sie im Bereich zwischen (0,1) ab.

Nachdem wir nun verstanden haben, was ein einzelnes Neuron für Funktionen hat und was die einzelnen Schritte innerhalb des Knotens sind, können wir uns nun dem Künstlichen Neuronalen Netzwerk zuwenden. Dies ist lediglich eine Sammlung dieser Neuronen, die in verschiedenen Schichten organisiert sind. 

Die Informationen durchlaufen das Netzwerk in verschiedenen Schichten:

• Eingabeschicht: Hier werden die Inputs für das Modell eingegeben und in den Neuronen verarbeitet, bevor sie weitergereicht werden an die nächste Schicht. 
• Verborgene Schicht(en): Eine oder mehrere sogenannte Hidden Layer übernehmen die eigentliche Informationsverarbeitung. Die Eingaben aus vorherigen Schichten werden gewichtet in einem Neuron verarbeitet und an die nachfolgende Schicht weitergegeben. Dies geschieht solange bis die Ausgabeschicht erreicht ist. Da die Berechnungen in dieser Schicht nicht sichtbar sind, sondern im “verborgenenen” stattfinden, werden diese Ansammlungen an Neuronen als Hidden Layers oder verborgenenen Schichten bezeichnet. 
• Ausgabeschicht: Diese Schicht schließt an die letzte verborgene Schicht an und übernimmt die Outputs der Neuronen. Die Ergebnisse der Knoten in diesem Layer beinhalten das schlussendliche Ergebnis bzw. die Entscheidung des Neuronalen Netzwerks dar. 

Im Zusammenhang mit KI wird oft davon geredet, dass die Modelle trainiert werden müssen und viele Daten benötigt werden, um gute Ergebnisse liefern zu können. Doch was bedeutet dieser Prozess genau für das Künstliche Neuronale Netzwerk?

Aus den Daten wird für jeden einzelnen Datensatz das Ergebnis berechnet, das beim Durchlaufen des Netzwerks entsteht und verglichen, wie gut das Ergebnis des Netzwerkes ist im Vergleich zu dem tatsächlichen Ergebnis aus dem Datensatz. Dabei soll die Vorhersage des Künstlichen Neuronalen Netzwerkes immer genauer an das tatsächliche Ergebnis herankommen. 

Das Neuronale Netzwerk hat dazu eine Stellschraube, um das Ergebnis mit jedem Trainingsschritt an den tatsächlichen Outcome heranbringen zu können, nämlich die Gewichtung der Outputs der einzelnen Neuronen. Im Lernprozess werden deren Gewichtungen ständig verändert, um die Genauigkeit des Ergebnisses zu verändern. Das heißt jedes Neuron entscheidet, welche Outputs der vorhergegangen Neuronen für ihre Berechnung wichtig sind und welche nicht. Im besten Fall festigt sich dieses Gewicht mit jedem neuen Datensatz und das gesamte Ergebnis wird genauer. 

Hierzu ein kleines Beispiel zur Verdeutlichung, welches selbstverständlich nicht zur Nachahmung empfohlen wird. Im Mathe Unterricht sitzen insgesamt drei gute FreundInnen neben dir. Bei jeder Aufgabe, die im Unterricht gerechnet wird, kannst du alle drei fragen, ob sie dir ihr Ergebnis nennen, weil du selbst nicht weiterkommst. Alle drei nennen dir auch immer bereitwillig eine Zahl als Lösung. Deshalb möchtest du während den Unterrichtsstunden (der Trainingsphase) herausfinden, welcher der drei Mitschüler meistens das beste Ergebnis hat. 

Bei jeder Aufgabe, die ihr rechnet, fragst du also alle drei nach ihrem Ergebnis und entscheidest dich für eins, um es dann mit dem Ergebnis der LehrerIn zu vergleichen und herauszufinden, von welchem der drei MitschülerInnen du das beste Ergebnis erwarten kannst. Je nach Teilgebiet erkennst du, dass ein Input besser ist als ein anderer. Somit änderst du die Gewichtungen in der Trainingsphase ab und verfeinerst sie. In der Klausur weißt Du dann im Optimalfall genau, an welchen der drei Du dich wenden musst, um möglichst das korrekte Ergebnis genannt zu bekommen. 

Genau das machen auch alle Neuronen im Netzwerk. Sie bekommen während dem Training eine gewisse Anzahl von Inputs genannt, abhängig davon, wie viele Neuronen in unmittelbarer Nähe “sitzen”. Im Training entscheiden sie sich in jedem Schritt, welches Vorergebnis für sie am Besten geeignet ist und vergleichen dann mit dem tatsächlichen Ergebnis, um festzustellen, ob sie richtig lagen. Nach dem Training, also in der Klausur, wissen sie dann genau, welche vorherigen Neuronen die wichtigsten sind. 

Was sind Vorteile und Herausforderungen der multivariaten Analyse?

Die Methoden der multivariaten Analyse sind mächtige Werkzeuge bei der Arbeit mit großen Datensätzen und der Erkennung von Strukturen und Zusammenhängen darin. Im Vergleich zur univariaten oder bivariaten Analyse bietet sie deutlich mehr Einblicke in die komplexen Beziehungen innerhalb der Daten und schafft dadurch ein besseres Verständnis. Jedoch hat die Anwendung der multivariaten Analyse auch einige Herausforderungen, welche wir uns in diesem Abschnitt zusammen mit den Vorteilen genauer anschauen. 

Zu den Vorteilen der multivariaten Analyse zählen zum Beispiel: 

• Besseres Verständnis komplexer Beziehungen: Durch die Möglichkeit die Beziehungen zwischen mehreren Variablen untereinander genauer zu analysieren, werden auch sehr komplexe Beziehungen für Forscher quantifizierbar und ersichtlich. Diese Zusammenhänge sind mit einfacheren Methoden häufig nicht erkennbar. 
• Erkennung latenter Variablen: Es gibt unterschiedliche multivariate Methoden, die zur Identifikation von sogenannten latenten Variablen genutzt werden können. Dabei handelt es sich um nicht direkt messbare Konstrukte, welche aus den beobachteten Daten abgeleitet werden können, wie zum Beispiel in der Psychologie die Empathie. Dafür kann beispielsweise die Faktorenanalyse genutzt werden. 
• Effiziente Nutzung von Daten: Durch die Einbeziehung von mehreren Variablen in die gleichzeitige Auswertung wird der gesamte Datensatz und die darin enthaltenen Informationen besser genutzt und alle erkennbaren Strukturen aufgedeckt. 

Neben diesen Vorteilen hat die Anwendung von multivariaten Methoden auch einige Herausforderungen, die bei der Implementierung beachtet werden sollten: 

• Hohe Modellkomplexität: Der Aufbau von multivariaten Modellen ist häufig komplex und fordert ein tiefes Verständnis der zugrundeliegenden Statistik, damit optimale Ergebnisse erzielt werden können. Außerdem sind Modelle, welche mehrere Variablen einbeziehen, auch schwieriger zu interpretieren und zu validieren, sodass in diese Schritte mehr Arbeit fließen muss, um nutzbare Ergebnisse erzielen zu können. 
• Anforderungen an die Datenqualität: Die Datenqualität spielt bei solch komplexen Methoden eine noch wichtigere Rolle, damit belastbare Ergebnisse erzielt werden können. Es muss sichergestellt werden, dass der Datensatz vollständig ist, also keine fehlenden Werte vorhanden sind, und dass die Konsistenz gegeben ist, also keine fehlerhaften Werte enthalten sind, welche die Ergebnisse negativ beeinflussen könnten. Außerdem setzen manche Verfahren, wie zum Beispiel PCA, eine Standardisierung der Daten voraus, damit nicht fälschlicherweise dominante Effekte entstehen, welche lediglich auf unterschiedliche Skalen zurückzuführen sind. 
• Interkorrelationen: Wenn die unabhängigen Variablen stark miteinander korrelieren, also eine sogenannte Multikollinearität im Datensatz vorliegt, kann die Stabilität und die Interpretationsfähigkeit des Modells darunter leiden. Diese Korrelationen müssen deshalb frühzeitig entdeckt werden und es sollte möglicherweise nur eine der miteinander korrelierten Variablen im Datensatz verbleiben. 
• Overfitting: Durch die steigende Anzahl von Variablen und die höhere Modellkomplexität erhöht sich auch das Risiko für Overfitting, also, dass das Modell spezifische Eigenschaften des Datensatzes auswendig lernt und sich nicht mehr darauf konzentriert, die grundlegenden Strukturen zu erkennen. Dies führt dazu, dass das Modell bei neuen Daten nur schlechte Vorhersagen liefert. 
• Rechenintensivität: Insbesondere bei großen Datensätzen sind viele der vorgestellten Modelle sehr rechenintensiv, sodass nicht nur längere Trainingszeiten in Kauf genommen werden müssen, sondern möglicherweise auch speziellere Hardware, wie zum Beispiel Grafikkarten, benötigt werden. 

Die multivariate Analyse bietet viele Vorteile bei der Arbeit mit komplexen Datensätzen und der Erstellung von aussagekräftigen Modellen. Jedoch haben diese auch mit einigen Herausforderungen zu kämpfen, da zum Beispiel mehr Rechenressourcen benötigt werden und die Datenqualität sehr hoch sein muss, um belastbare Vorhersagen tätigen zu können.

Das solltest Du mitnehmen

• Die multivariate Analyse umfasst Methoden, die darauf ausgerichtet sind, den Zusammenhang zwischen mehreren Variablen zu erkennen und zu quantifizieren.
• Die multivariaten Analysen werden in strukturprüfen Methoden, welche eine Hypothese als Grundlage nutzen, und strukturentdeckende Methoden, die komplett selbstständig Zusammenhänge erkennen, unterteilt.
• Multivariate Analysen haben den Vorteil, dass sie auch latente Variablen erkennen können, die nicht direkt im Datensatz vorhanden sind, und außerdem den Datensatz effizienter nutzen, da alle Informationen und deren Zusammenhänge abgebildet werden können.
• In diesem Beitrag haben wir verschiedene multivariate Analysemethoden vorgestellt, wie zum Beispiel Künstliche Neuronale Netzwerke oder die Hauptkomponentenanalyse.

Andere Beiträge zum Thema Multivariate Analyse

Einen interessanten Artikel über die Multivariate Analyse und andere Typen findest Du auf Medium.