Autoencoders are a special form of deep neural networks primarily used for feature extraction or dimension reduction. As they can work with unlabeled data, they belong to the field of unsupervised learning. The architecture consists of two main components: the encoder, which compresses the input data into a low-dimensional representation, and the decoder, trained to reconstruct the original data from this representation.

This article provides a detailed overview of the structure of autoencoders and explains the individual components of the architecture. We also look at the challenges that can arise during training and the applications that build on this model. Finally, we take a closer look at the advantages and disadvantages of the method and compare it with other dimension reduction algorithms.

What is an Autoencoder?

An autoencoder is a special form of artificial neural network trained to represent the input data in a compressed form and then reconstruct the original data from this compressed form. What initially sounds like an unnecessary transformation is an integral part of dimensionality reduction, as it allows irrelevant details or noise to be removed from the data set. The reduction of the data set takes place in the so-called encoder, while the second component, the decoder, reconstructs the original data.

As autoencoders independently learn the patterns and structures in the input data, they belong to the field of unsupervised learning, as no labels are required in the data set. This means they can be used in a variety of applications, even if no labeled data is available. This characteristic makes them a versatile tool in deep learning.

How is an Autoencoder structured?

An autoencoder is a special neural network that aims to compress the input data as much as possible and then restore the original data as accurately as possible from this compression. These tasks are performed by the two main components, the encoder and the decoder, which are described in more detail in this chapter.

Encoder: Data compression and feature extraction:

The encoder is the first part of the autoencoder architecture in which the data is further compressed from layer to layer until it finally ends up in the so-called bottleneck or latent space. To do this, the data passes through various neural layers, with each of these layers having progressively fewer output parameters, which means that the model has to extract the most important features from the data.

The following features characterize the encoder:

• Data reduction: The encoder is designed to remove irrelevant information from the data set and retain only the most important features. To do this, the high-dimensional data is gradually transformed into a low-dimensional space and during training the encoder becomes better and better at retaining the important information.
• Non-linear transformations: Various non-linear activation functions, such as ReLu (Rectified Linear Unit) or sigmoid, are used to be able to recognize even complex structures in the data. These enable more complex relationships to be recognized and mapped.
• Bottleneck structure: At the end of the encoder is the so-called bottleneck, which represents the point in the model at which the data has been compressed the furthest and is therefore available in the lowest dimension. Only a small amount of memory is available in this layer, which forces the model to compress the data as much as possible.

The encoder is therefore the first part of an autoencoder in which the information from the data set is increasingly compressed and the number of dimensions is reduced.

Latent Space/Bottleneck

The encoder structures are followed by the so-called latent space or bottleneck, which is a central component of the autoencoder. In this state, the data has the lowest possible dimensional representation and still has as much information content as possible, which should enable the subsequent decoder to restore the input data.

Decoder: Recovering data from the latent space

The decoder is the counterpart to the encoder and generates data in its original form from the compressed representation in latent space. The decoder also consists of several layers and gradually increases the dimensions again until the high-dimensional space of the initial data is reached again. The following features are decisive here:

• Unfolding the data: The decoder works in exactly the opposite way to the encoder and instead of compressing data, it unfolds the data. Each neural layer in the decoder adds dimensions to the data set until the original data form is restored.
• Reconstruction of the data: The goal of the decoder is to restore the original form of the data set, getting as close as possible to the original data and mapping the important features.
• Output layer: The output layer is concerned with outputting the predictions in their original form. Depending on the application, certain specifications must be adhered to. When processing images, for example, the pixel values that make up the image must lie within a certain range. Special activation functions can be used to ensure that these requirements are met.

A good decoder is characterized by the fact that it can generate data in the original form from the essential information of the compressed representation, which comes as close as possible to the elements from the data set.

The autoencoder aims to adjust the parameters of these components in such a way that the so-called reconstruction error is minimized. This means that the difference between the input and output data is as small as possible. In the case of image processing, the original image that is fed to the autoencoder should be generated again at the end of the autoencoder with as much detail as possible. For the model to improve further, it undergoes iterative training, which we will look at in more detail in the next section.

How does the Autoencoder learn?

During training, the autoencoder is optimized to reconstruct the input data, such as an image, as accurately as possible. The difficult thing is that the decoder does not have the original image at its disposal, but only the highly compressed version of the data in the latent space that was generated by the encoder. The training therefore has two objectives:

1. The encoder must learn as good a representation of the data as possible, which consists of only a few dimensions but still contains the most important features of the data.
2. The decoder must become better at building a high-dimensional form from this low-dimensional data representation, which differs little or preferably not at all from the input data.

The training comprises several steps, which are essential for an optimal result.

Data Preparation

Although the autoencoder does not require labels in the data set, it is still advisable to prepare the data set before training to make it easier for the model and achieve faster convergence. For this purpose, the data is normalized or scaled, which means that the values of the data are all on the same scale.

Forward Pass

During the forward pass, the data is fed through the model from the front, i.e. first through the encoder. This calculates a low-dimensional representation, the latent space, which is then fed back into higher dimensions in the decoder, reproducing the original data as accurately as possible.

The autoencoder therefore finds ways of compressing the input data as well as possible and recreating the data points with the original dimensionality from this compressed data. However, to come as close as possible to the input data, a metric is required to measure how well the autoencoder does this.

Calculating the Loss Function

To enable the autoencoder to assess whether it is moving in the right direction, it uses the so-called loss function to calculate a reconstruction error. This makes a statement about how much the data created by the autoencoder differs from the original data. In the best-case scenario, this difference is as small as possible and the predicted data differs only minimally from the data in the data set.

For example, the mean squared error, which calculates the average squared deviation of all training examples, can be used as a loss function or reconstruction error:

\(\)\[MSE=\frac{1}{n}\sum_{i=1}^{n}\left(x_i-\hat{x_i}\right)^2 \]

Here, \(x_{I}\) is the actual value in the data set, and \(\hat{x_i}\) is the value predicted by the model. The training process aims to further minimize this function in each iteration.

Backward Pass & Optimization

Once the error has been calculated for an iteration, it can be used to move backward through the model using backpropagation. The weights of the individual neurons are adjusted so that the error is smaller in the next pass. To do this, calculations are performed in each neural layer that results in the rate of change of the weight. However, the full change is not used, instead, the so-called learning rate is used as a hyperparameter, which determines how strong the calculated change is. A learning rate that is too high can lead to an unstable and very erratic model, while a low learning rate means that the model only improves slowly.

Autoencoders usually use gradient descent as an optimization algorithm, in which the opposite direction of the derivative determines the change in weights. In addition, the so-called Adam Optimizer can also be used, which is a special form of gradient descent.

Iterative Learning

These described processes with forward pass and backward pass are now constantly repeated and several so-called epochs are run through. An epoch comprises so many iterations that each data point in the training data set has been used once in training. Several of these epochs are run through in a training session, whereby the reconstruction error should continuously decrease. This process is then repeated until either the error of the autoencoder is minimized, a maximum number of iterations is reached or no more significant improvements can be observed.

Hyperparameter Tuning

After a full training run, the autoencoder’s learning process is not yet complete. If you are not yet satisfied with the results or you want to test whether they can be further improved, you can use hyperparameter tuning.

Hyperparameters are certain properties in the model architecture that cannot be changed independently during training but are set externally. These include, for example, the learning rate, the number of layers in the decoder and encoder or the number of dimensions in the latent space. During hyperparameter tuning, an attempt is made to find the optimum settings for these hyperparameters by carrying out certain tests and trying out different training runs with different hyperparameter values.

Training an autoencoder is a comprehensive process that aims to minimize the reconstruction error as much as possible. By going through the above steps, a meaningful and robust model can be trained.

What Types of Autoencoders are there?

Over time, different types of autoencoders have been developed, which are specialized for certain data types or use cases. Each of these model variants has its characteristics and advantages, which we will describe in more detail in this section.

Basic Autoencoder

The basic autoencoder is the simplest form of autoencoder and is characterized by its symmetrical shape. The encoder reduces the data to a low-dimensional representation and the decoder attempts to reconstruct the original data from this representation.

• Structure: Both encoder and decoder consist of neural network layers that are completely interconnected so that each neuron in one layer is connected to all neurons in the subsequent layer. The structure is similar to a bottleneck, with the narrowest point representing the so-called latent space.
• Application: The basic autoencoder is mainly used for simple tasks in dimension reduction or feature extraction.
• Advantage: Thanks to their simple structure, these models can be trained quickly and are easy to understand.

Denoising Autoencoder

The denoising autoencoders were developed to eliminate noise in data, i.e. errors and impurities. This allows the input data to be cleaned or filtered. During training, noise is deliberately mixed into the input data and the model must still attempt to generate the original input data without noise.

• Functionality: The structure of the denoising autoencoder is similar to a basic autoencoder with the difference that it receives contaminated data. During training, the encoder attempts to generate a compressed representation despite the noise, with the help of which the decoder can generate the input data without noise.
• Application: These models are mainly used in image processing to clean up blurred or noisy images and thus improve their quality. Denoising autoencoders can also be used to suppress background noise in signal processing.

Variational Autoencoder (VAE)

Variational autoencoders are a further development of the basic autoencoder, in which the latent space does not learn a fixed representation of the data, but rather generates a probability distribution.

• Latent Space: The latent space in a variational autoencoder is modeled as a probability distribution and, in most cases a normal distribution. This enables the model to generate smoother and softer transitions.
• Application: VAEs are mainly used in the field of generative AI, for example, to generate images or audio files that should appear as realistic as possible.
• Advantage: Due to the probabilistic nature of VAEs, these models are particularly suitable for applications in which a statistical representation of the data is important, such as anomaly detection.

Convolutional Autoencoder

Convolutional autoencoders comprise specially adapted models for image processing. The layers from convolutional neural networks are used to process the input data more efficiently than with a dense neural network and to extract the relevant image features.

• Structure: Classic convolutional layers are used in the encoder, which can learn the important image properties and their position. The decoder, on the other hand, uses up-sampling layers, also known as transposed convolutions, to restore the image.
• Application: CAEs are used in many image processing applications, such as image compression, image denoising or for complex image generation.
• Advantage: Compared to classic autoencoders, the convolutional layers can be used to better address the special features of image processing.

These variants are just some of the many specialized autoencoders that have been adapted for a wide range of applications. It is important to know the differences and their advantages to make the right choice and thus achieve even better results for the respective data set.

What are the Challenges in training Autoencoders?

Autoencoders are a powerful tool in dimension reduction and feature extraction, which can also recognize and map complex relationships in the data structure. However, this complexity also has its pitfalls, as overfitting can quickly occur and the reconstruction quality of new data is not good enough. To get the maximum performance out of autoencoders, you should consider the points explained in more detail in this section.

Shallow vs. Deep Autoencoders

Depending on the number of layers in the encoder and decoder, a distinction is made between shallower and deeper architectures. The complexity depends heavily on the data and the objective.

• Shallow Autoencoders: In this architecture, fewer layers are used in the encoder and decoder, which means that the model can only capture less complex relationships, but also requires less computing power and may complete training more quickly. Shallow autoencoders are particularly useful for less complex tasks and datasets, as they can extract the relevant features and have a lower probability of overfitting due to the smaller number of parameters.
• Deep Autoencoders: With a deep autoencoder architecture, encoders and decoders have more layers and can therefore learn more complex correlations that arise, for example, with highly complex data, such as images, or with more difficult tasks, such as feature extraction. However, it must be noted that the risk of overfitting increases and regularization techniques may therefore be necessary.

The decision for the right architecture of the autoencoder has a decisive influence on the quality of the predictions and the duration of the training. Depending on the data and the desired predictions, enough layers should be used to map the complexity and yet only enough to avoid overfitting.

Reconstruction Quality

The main aim of the autoencoder is to be able to create the most detailed possible replicas of the input data and thus keep the reconstruction error as low as possible. This ability depends on various factors that should be taken into account:

• Size of the Latent Space: The compressed representation of the input data is stored in the latent space. If possible, the dimensionality should be selected so that the decoder still contains enough information to reconstruct the input data and the latent space is still small enough to ensure that a dimensional reduction has taken place. A choice must therefore be made that balances the extremes between compression and information content.
• Decoder Architecture: In practice, people often tend to underestimate the importance of the decoder and concentrate primarily on the encoder and the latent space. However, care should be taken to ensure that the decoder is well constructed so that a detailed reconstruction can be created from the compressed data.
• Activation and Loss Function: The reconstruction depends to a large extent on the correct choice of these two functions. They determine whether the model can only learn linear or non-linear relationships and how well the training process can run.

The autoencoder is a complex machine-learning model that can capture very complex relationships if it is set up correctly. Therefore, special attention must be paid to choosing the right architecture to get the most out of the models.

How can an Autoencoder be created in Python with TensorFlow?

In Python, autoencoder models can be easily created with Keras, which is part of TensorFlow. In this example, we will use the MNIST dataset, which contains images of handwritten digits. To do this, we will define an encoder and decoder with different layers and then train the model. Finally, we will test the performance of the model by comparing some training images and their prediction.

To build the autoencoder, we need some libraries and functionalities. With the help of NumPy, we can prepare the data set so that the model can use it later. We will use Matplotlib at the end of the example to output the original images and the reconstructed images.

TensorFlow will be used to build the final model using the Keras module. First of all, we import the data set mnist that we want to use. We also import the Model functionality to build the autoencoder, and with the help of the Input and Dense layers, we can later build the model piece by piece.

We can load the MNIST data set using the load_data() function and split it directly into training and test data sets. To allow the model to focus on the characteristics of the data, we normalize the data to the range from 0 to 1. Each pixel in the image can have a numerical value from 0 to 255. We normalize the values by dividing by 255. This is also useful because we will build the model to predict a value between 0 and 1 for each pixel so that the input and output data are directly comparable.

The data sets are then stored in a central vector, which has the length of the data set as the first dimension and the number of pixels in an image as the second dimension. For the MNIST dataset, the training dataset consists of 6,000 images, with each image having 784 pixels.

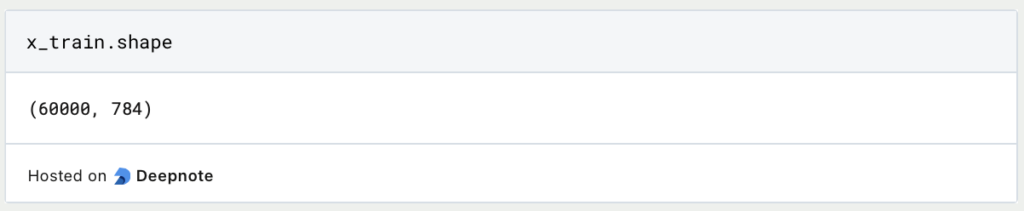
Now comes the exciting part, in which we build the model and define the individual layers. To do this, we specify that the latent space should only have a total of 32 dimensions instead of 784. This is a hyperparameter that we set and that does not change during training. If we determine after the first training run that it is incorrectly selected, we can test a higher or lower dimensionality in a further training run.

The encoder consists of the input layer with 784 input neurons, i.e. one for each pixel in the image. This is followed by a dense layer, which consists of only 128 neurons and thus reduces the dimensionality in the first step. We use ReLu as the activation function, as it is a good starting point for many deep-learning models. A dense layer is then used again, which then only has 32 neurons for the latent space.

The decoder connects to the latent space and increases the dimensionality again from 32 to 128 neurons. As the last layer, the dimensionality is increased again to 784, which is the same as the input data. In the last layer, we use the sigmoid activation function, as this scales the output values to the range between 0 and 1, so that the prediction of the model is also comparable with the input data.

The model can then be defined simply by passing the first and last layers of the model as parameters. We then define the encoder and decoder models, which we can use later to calculate and output the predictions on the test set.

With the help of summary(), we can visualize the architecture of the autoencoder and see the individual layers and their dimensionality.

Now that the model and the individual layers have been defined, the only thing missing is the definition of the loss function and the optimization algorithm so that the model knows how to adjust the weights of the neurons after each training epoch. In our case, we use binary cross-entropy because the autoencoder returns values between 0 and 1 in the last layer.

The model is then trained for a total of 50 epochs, i.e. the training data set is run 50 times, with 256 images being transferred in each batch. After each epoch, x_test is used as a validation dataset to check how the model reacts to new data.

After training, we check the model by outputting a total of ten images from the dataset and looking at the reconstructed images from the autoencoder. To do this, we use the previously defined encoder and decoder models to first compress the images to the latent space and then reconstruct them. We then output them using Matplotlib and see that the reconstructions are very close to the original images except for small details.

This simple autoencoder has already achieved good results on the black-and-white images. It can now be used, for example, to compress the images and thus store them in a version that requires less memory.

How do Autoencoders compare with other Dimension Reductions?

The introduction of autoencoders has provided a method of effectively compressing data and removing superfluous features from the data. However, other established methods for dimension reduction may still be more suitable depending on the use case. In this section, we want to give an overview of the cases in which which method may be most suitable.

PCA vs. Autoencoder

Principal Component Analysis assumes that several variables in a data set may measure the same thing, i.e. that they are correlated. These different dimensions can be mathematically combined into so-called principal components without compromising the significance of the data set. To do this, the eigenvectors with the highest eigenvalues are used as a linear combination of existing dimensions, thereby reducing the dimensionality.

In contrast to autoencoders, PCA is a linear method and should therefore only be used if the data follows a linear structure. Autoencoders, on the other hand, can also learn and map non-linear relationships thanks to the neural network architecture.

However, the linear combinatorics of PCA make it easier to interpret the new dimensions and they can usually also be divided into certain areas. With autoencoders, on the other hand, the dimensions in the latent space are much more difficult to interpret, as they are calculated from the neural layers, which can quickly become very confusing.

Finally, the principal component analysis requires significantly less computational effort due to the simple methodology, so that it can be calculated quickly and easily for smaller data sets. The autoencoder is much more complex and training can quickly take several minutes or hours.

t-SNE vs. Autoencoder

t-Distributed Stochastic Neighbor Embedding (t-SNE for short) is based on the idea that the dimensions in a data set can be reduced by finding a probability distribution that maps the distances between data points in a high-dimensional space as accurately as possible in a low-dimensional space. Simply put, this is to ensure that the points that were close to each other in the high-dimensional space, i.e. neighbors, are also close to each other in the low-dimensional space.

t-SNE is primarily used to visualize data in two- or three-dimensional space to obtain an initial overview of the data and its position. Autoencoders, on the other hand, are much more versatile and can also be used for feature extraction or dimension reduction with a freely selectable number of dimensions, for example.

Both t-SNE and autoencoders can recognize non-linear relationships in the data and map them accordingly in low-dimensional space. However, t-SNE is often significantly more computationally intensive than autoencoders and scales very poorly with large data sets. The calculation is therefore often slower than with comparable autoencoders.

What further developments are there in this area?

Autoencoders have been a central component of the further development of machine learning in recent years. They have brought extensive progress in many areas, although this section will focus primarily on the work in the field of generative models and transfer learning that builds on them.

Generative Models

By changing from conventional autoencoders to variational autoencoders (VAE), the models were able to learn not only a deterministic representation of the data but also an underlying data distribution. This small change made it possible for the autoencoders to also generate new data points by sampling the data distribution. This resulted in generative models, which are used, for example, in the field of image and speech generation to create realistic and variant-rich data that is, however, completely artificial.

In addition, autoencoders have also indirectly given rise to so-called generative adversarial networks (GANs for short), which are based on the architecture of two opposing models. Unlike autoencoders, these are called generators and discriminators and do not work together, but against each other. The generator tries to create images or similar that are as close to reality as possible and passes them on to the discriminator.

The discriminator in turn tries to find out whether the data is artificial or real. In the course of the training, this counterplay results in the generator becoming better and better at creating artificial data that is hardly any different from reality and the discriminator in turn becoming better and better at recognizing these fakes.

Transfer Learning

Another important development, which has also been driven by autoencoders, is transfer learning. Autoencoders are trained to recognize important features in data sets, such as images, and extract them from the input data. This led to the approach of using the encoder part of the model as a feature extractor for other models and using it as the basis for further training steps.

This resulted in the method of no longer training complete models from scratch, but rather using certain pre-trained parts and then adapting them to the specific data set. This approach can save a lot of time and, above all, computational effort, especially when it comes to large and complex data sets.

This is what you should take with you

• Autoencoders are machine learning models that consist of an encoder and a decoder and are used for dimension reduction or feature extraction.
• In addition to the basic autoencoder, many types of autoencoders have been developed that have been optimized for specific use cases.
• When training an autoencoder, care should be taken to use the correct architecture of the layers to be able to map the complexity in the data set and still minimize the risk of overfitting.
• In Python, autoencoders can be built using TensorFlow and Keras. The layers can be defined individually to vary the steps for data compression.
• When it comes to dimensionality reduction, autoencoders are characterized by the fact that they can also map non-linear dependencies compared to PCA and are usually more computationally efficient than t-SNE, for example.
• Autoencoders have laid a decisive foundation stone in the development of machine learning models, as they have indirectly given rise to generative models and transfer learning.

Other Articles on the Topic of Autoencoders

TensorFlow has an interesting and detailed article on the topic that you can find here.